Пространственная обработка с помощью управляющих матриц для псевдослучайного управления передачей в многоантенной системе связи

Пространственная обработка с помощью управляющих матриц для псевдослучайного управления передачей в многоантенной системе связи

Иллюстрации

Показать все

Реферат

ОБЛАСТЬ ТЕХНИКИ, К КОТОРОЙ ОТНОСИТСЯ ИЗОБРЕТЕНИЕ

Настоящее изобретение в целом относится к передаче данных, а более точно к технологиям для выполнения пространственной обработки для передачи данных в многоантенной системе связи.

ПРЕДШЕСТВУЮЩИЙ УРОВЕНЬ ТЕХНИКИ

Многоантенная система связи применяет многочисленные передающие антенны и единственную или многочисленные принимающие антенны для передачи данных. Многоантенная система, таким образом, может быть системой с многими входами и многими выходами (MIMO) или системой с многими входами и одним выходом (MISO). Система MIMO применяет множество (N_T) передающих антенн в передающем объекте и множество (N_R) принимающих антенн в принимающем объекте при передаче данных и обозначается как система N_RN_T. Канал MIMO, сформированный N_T передающими антеннами и N_R принимающими антеннами, может быть разложен на N_S пространственных каналов, где N_Smin{N_T, N_R}. N_S пространственных каналов могут использоваться для передачи данных таким образом, чтобы добиться большей надежности и/или более высокой общей пропускной способности. Система MISO применяет множество (N_T) передающих антенн и единственную принимающую антенну при передаче данных. Канал MISO, сформированный N_T передающими антеннами и единственной принимающей антенной, является состоящим из единственного пространственного канала.

Каждый пространственный канал может испытывать различные пагубные канальные воздействия, например, замирание, многолучевое распространение и влияние помех. N_S пространственных каналов канала MIMO также могут испытывать разные канальные влияния и могут достигать разных отношений сигнал/шум и помеха (SNR). SNR пространственного канала определяет его пропускную способность, которая типично количественно определяется конкретной скоростью передачи данных, при которой могут надежно передаваться данные по пространственному каналу. Для меняющегося во времени беспроводного канала состояние канала меняется со временем, и SNR каждого пространственного канала также меняется со временем.

Чтобы максимизировать пропускную способность многоантенная система может использовать некоторую разновидность обратной связи, посредством которой принимающий объект оценивает пространственные канал(ы) и предоставляет информацию обратной связи, указывающую состояние канала или пропускную способность каждого пространственного канала. Принимающий объект затем может настраивать передачу данных по каждому пространственному каналу на основании информации обратной связи. Однако эта информация обратной связи может не быть доступной по различным причинам. Например, многоантенная система может не поддерживать передачу обратной связи из принимающего объекта или беспроводной канал может изменяться быстрее, чем скорость, с которой принимающий объект может оценивать беспроводной канал и/или отправлять обратно информацию обратной связи. В любом случае если передающий объект не имеет представления о состоянии канала, то ему может понадобиться передавать данные на низкой скорости с тем, чтобы передача данных могла надежно декодироваться принимающим объектом даже вопреки наихудшему состоянию канала. Эксплуатационные показатели такой системы диктовались бы ожидаемым наихудшим канальным состоянием, что является в высшей степени нежелательным.

Чтобы улучшить эксплуатационные показатели, когда информация обратной связи не доступна, передающий объект может выполнять пространственную обработку из условия, чтобы передача данных не придерживалась наихудшего канального состояния в течение длительного периода времени, как описано ниже. В таком случае для передачи данных может использоваться более высокая скорость. Однако эта пространственная обработка представляет дополнительную сложность для передающего объекта и возможно принимающего объекта.

Поэтому в данной области техники есть необходимость в технологиях для выполнения пространственной обработки с минимальной сложностью, чтобы улучшить производительность передачи данных в многоантенной системе связи.

СУЩНОСТЬ ИЗОБРЕТЕНИЯ

Технологии для формирования и использования управляющих матриц для псевдослучайного управления передачей (PRTS) описаны в материалах настоящей заявки. PRTS относится к пространственной обработке, выполняемой передающим объектом с помощью управляющих матриц с тем, чтобы передача данных придерживалась набора «эффективных» каналов. Эти эффективные каналы формируются реальным каналом MIMO или MISO, используемым для передачи данных, и управляющими матрицами, используемыми для PRTS. При PRTS передача данных не придерживается единственной реализации плохого канала в течение длительного периода времени, и эксплуатационные показатели не диктуются наихудшим канальным состоянием.

Управляющие матрицы могут формироваться из условия, чтобы упрощалось вычисление для PRTS. Множество управляющих матриц может быть сформировано, прежде всего, посредством выбора базовой матрицы, которая может быть матрицей Уолша, матрицей Фурье или некоторой другой унитарной матрицей, содержащей ортогональные столбцы. Затем выбираются разные комбинации скаляров, причем каждая комбинация включает в себя, по меньшей мере, один скаляр для, по меньшей мере, одной строки базовой матрицы, один скаляр на строку. Каждый скаляр может быть вещественным или комплексным значением. Разные управляющие матрицы формируются посредством умножения базовой матрицы на каждую из разных комбинаций скаляров, как описано ниже. Разные управляющие матрицы, таким образом, являются разными перестановками базовой матрицы и сохраняют определенные желательные (например, унитарную) характеристики базовой матрицы. Посредством выбора подходящей базовой матрицы (например, матрицы Уолша) и подходящих скаляров (например, +1, -1, +jи -j, где элементы управляющих матриц находятся в множестве, состоящем из {+1,-1, +j, -j}. В этом случае перемножение символа данных с элементом управляющей матрицы может быть достигнуто простыми поразрядными операциями, как описано ниже.

Множество управляющих векторов, используемых для передачи MISO, может быть сформировано столбцами управляющих матриц. Каждый управляющий вектор также может рассматриваться как вырожденная управляющая матрица, содержащая только один столбец. Различные аспекты и варианты осуществления изобретения более подробно описаны ниже.

КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ

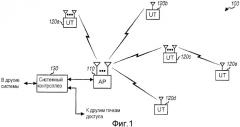
Фиг. 1 показывает многоантенную систему с точкой доступа и пользовательскими терминалами;

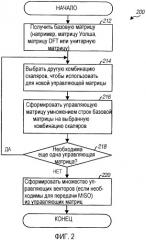
фиг. 2 показывает последовательность операций для формирования управляющих матриц и управляющих векторов, используемых для псевдослучайного управления передачей; и

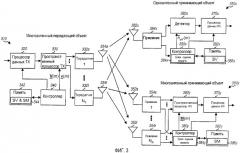
фиг. 3 показывает структурную схему многоантенного передающего объекта, одноантенного принимающего объекта и многоантенного принимающего объекта.

ПОДРОБНОЕ ОПИСАНИЕ

Слово «примерный» используется в материалах настоящей заявки, чтобы иметь значение «служащий в качестве примера, отдельного случая или иллюстрации». Любой вариант осуществления, описанный в материалах настоящей заявки в качестве «примерного», не обязательно должен быть истолкован как предпочтительный или преимущественный над другими вариантами осуществления.

Фиг. 1 показывает многоантенную систему 100 с точкой 110 доступа (AP) и пользовательскими терминалами 120 (UT). Точка доступа обычно является стационарной станцией, которая поддерживает связь с пользовательскими терминалами и, к тому же, может упоминаться как базовая станция или некоторой другой терминологией. Пользовательский терминал может быть стационарным или мобильным и, к тому же, может упоминаться как мобильная станция, беспроводное устройство, абонентская аппаратура или некоторой другой терминологией. Системный контролер 130 присоединяется к точкам доступа и обеспечивает координацию и управление для этих точек доступа.

Точка 110 доступа оборудована множеством антенн для передачи данных. Каждый пользовательский терминал 120 может быть оборудован единственной антенной или множеством антенн для передачи данных. Пользовательский терминал может поддерживать связь с точкой доступа и, к тому же, может осуществлять одноранговую связь с другим пользовательским терминалом. В последующем описании передающий объект может быть точкой доступа или пользовательским терминалом, а принимающий объект также может быть точкой доступа или пользовательским терминалом. Передающий объект оборудован множеством (N_T) передающих антенн, а принимающий объект может быть оснащен единственной антенной или множеством (N_R) антенн. Передача MISO имеет место, когда принимающий объект оборудован единственной антенной, а передача MIMO имеет место, когда принимающий объект оборудован множеством антенн.

Система 100 может быть системой с единственной несущей или системой с многими несущими. Многочисленные несущие могут быть получены мультиплексированием с ортогональным частотным разделением каналов (OFDM), некоторыми другими технологиями модуляции многих несущих или некоторой другой конструкцией. OFDM эффективно разделяет всю ширину полосы пропускания системы на многочисленные (N_F) ортогональные подполосы, которые также упоминаются как тоны, поднесущие, элементы разрешения и частотные каналы. При OFDM каждая подполоса ассоциативно связана с соответственной поднесущей, которая может модулироваться данными.

В системе 100 передающий объект может передавать данные принимающему объекту с использованием псевдослучайного управления передачей (PRTS), чтобы достичь улучшенных эксплуатационных показателей. При PRTS передающий объект выполняет пространственную обработку из условия, чтобы передача данных придерживалась набора эффективных каналов и не застревала на единственной реализации плохого канала в течение длительного периода времени. Следовательно, эксплуатационные показатели не диктуются наихудшим канальным состоянием.

Пространственная обработка в передающем объекте для псевдослучайного управления передачей может быть выражена как:

х(m)=V(m)·s(m),

Рав. (1)

где s(m) - вектор N_T1 с вплоть до N_T символами данных, которые должны быть отправлены в диапазоне m передачи;

V(m) - управляющая матрица N_TN_T, используемая для диапазона m передачи; и

х(m) - вектор N_T1 с N_T символами передачи, которые должны быть отправлены с N_T передающих антенн в диапазоне m передачи.

В качестве используемых в материалах настоящей заявки «символом данных» является символ модуляции данных, «контрольным символом» (пилот-символом) является символ модуляции для пилот-сигнала, а «символом передачи» является символ, который должен быть отправлен с передающей антенны. Контрольные символы известны априори как передающему, так и принимающему объекту.

Диапазон передачи может покрывать временное и/или частотное измерения. Для системы с одной несущей диапазон передачи может соответствовать одному периоду символа, который является интервалом времени для передачи одного символа данных. Для системы со многими несущими, такой как система MIMO, которая использует OFDM, диапазон передачи может соответствовать одной подполосе в одном периоде OFDM-символа. Диапазон передачи также может покрывать многочисленные периоды символов и/или многочисленные подполосы. Так, mможет быть показателем для времени и/или частоты. Диапазон передачи также может упоминаться как интервал передачи, интервал сигнализации, временной интервал или некоторой другой терминологией.

Псевдослучайное управление передачей может использоваться для достижения разнесения передачи, пространственного кодирования с расширением спектра, а также может использоваться в сочетании с управляемой модой, как описано ниже. Пространственная обработка в принимающем объекте также описана ниже.

1. Формирование управляющей матрицы

Передающий объект может выполнять пространственную обработку для псевдослучайного управления передачей с помощью множества управляющих матриц (или матриц передачи), которые могут быть обозначены как или для i=1...L, где L может быть любым целым числом, большим одного. Управляющие матрицы должны быть унитарными матрицами и удовлетворять следующему:

, для i=1 ... L, Рав. (2)

где - единичная матрица с единицами по диагонали и нулями в других позициях. Каждая управляющая матрица включает в себя N_T столбцов и может быть выражена как . Равенство (2) показывает, что каждый столбец должен обладать единичной энергией, или , для a=1...N_T. Это условие гарантирует, что N_T символов данных, переданных одновременно с использованием , имеют одинаковую мощность. Равенство (2) также показывает, что Эрмитово скалярное произведение любых двух столбцов должно быть нулем, или , для a=1...N_T, b=1...N_S, и . Это условие гарантирует, что N_T символов данных, передаваемых одновременно, ортогональны один по отношению к другому на передающих антеннах.

Множество L управляющих матриц может быть сформировано различными способами. В варианте осуществления L управляющих матриц формируются из базовой матрицы, которая предпочтительно является унитарной матрицей. Базовая матрица может использоваться в качестве одной из L управляющих матриц. Другие L управляющих матриц могут быть сформированы умножением строк базовой матрицы на разные скаляры, как описано ниже. Вообще, скаляр может быть любым вещественным или комплексным значением. Однако, чтобы гарантировать, что управляющие матрицы являются унитарными матрицами, скаляры выбираются обладающими единичным модулем и фазой между 0 и 2π (или 0° и 360°).

В одном из вариантов осуществления базовая матрица является матрицей Уолша. Матрица Уолша 22 и матрица Уолша 44 могут быть выражены как:

и Рав. (3)

Матрица Уолша большей размерности может быть сформирована из матрицы Уолша меньшей размерности, как изложено ниже:

. Рав. (4)

Как показано равенством (4), матрицы Уолша имеют размерности, которые являются степенями двойки (например, 2, 4, 8 и так далее), вследствие способа, которым эти матрицы формируются.

Для системы N_R, при N_R2, четыре примерные управляющие матрицы могут быть сформированы из матрицы Уолша следующим образом:

где равна ;

получена умножением второй строки на -1 или ;

получена умножением второй строки на +j или ; и

получена умножением второй строки на -j или .

Дополнительные управляющие матрицы могут быть сформированы умножением второй строки на другие скаляры, например, и так далее. Множество L управляющих матриц может быть сформировано, как изложено ниже: и так далее, где масштабирование посредством имеет следствием, что каждый столбец из имеет единичную энергию.

Для системы N_R, при N_R4, четыре примерных управляющих матрицы могут быть сформированы из матрицы Уолша, как изложено ниже:

и

где равна ;

получена перемножением каждой из строк со 2 по 4 с ;

получена перемножением каждой из строк со 2 по 4 с +j; и

получена перемножением строки 2 с +j.

Множество L управляющих матриц может быть сформировано, как изложено ниже: и так далее, где масштабирование посредством имеет следствием, что каждый столбец имеет единичную энергию.

Вообще, для базовой матрицы NN каждая из строк со 2 по N базовой матрицы может быть независимо умножена на один из K разных возможных скаляров. Так, разных управляющих матриц могут быть получены из разных перестановок K скаляров для N-1 строк. Например, каждая из строк со 2 по N может быть независимо умножена на скаляр , , или . В этом случае для N=4 64 разных матрицы могут быть сформированы из матрицы Уолша с помощью четырех разных скаляров. Дополнительные управляющие матрицы могут быть сформированы с помощью других скаляров, например и так далее. Вообще, каждая строка базовой матрицы может быть умножена на любой скаляр, имеющий вид , где может быть любым значением фазы. К тому же, вообще, управляющие матрицы NN могут быть сформированы из матриц NN Уолша как , где .

Управляющие матрицы, выведенные на основании матрицы Уолша, имеют определенные желательные свойства. Если строки матрицы Уолша умножаются на скаляры ±1 и ±j,то каждый элемент результирующей управляющей матрицы будет равен +1, -1, +j или -j и, таким образом, имеет не нулевое значение только для вещественной или мнимой составляющей. В этом случае перемножение символа данных с элементом управляющей матрицы может быть выполнено простыми поразрядными операциями. Например, умножение комплекснозначного символа a + jb данныхна -1 может быть выполнено инвертированием знакового разряда обеих, вещественной и мнимой, составляющих символа данных, или (a + jb)(-1+j0)=. Умножение на +j может быть выполнено обменом местами вещественной и мнимой составляющих символа данных и инвертированием знакового разряда вещественной составляющей, или (a+jb)(j)=. Умножение на -j может быть выполнено обменом местами вещественной и мнимой составляющих символа данных и инвертированием знакового разряда обеих, вещественной и мнимой, составляющих, или (a+jb)(j)=. Таким образом, если элементы L управляющих матриц находятся в множестве, состоящем из , то вычисление, выполняемое передающим объектом для псевдослучайного управления передачей, может быть значительно упрощено.

В еще одном варианте осуществления базовая матрица является матрицей Фурье. Матрица Фурье равна матрице Уолша, или =. Матрица Фурье и матрица Фурье может быть выражена как:

и . Рав. (5)

Вообще, для матрицы Фурье элемент d_n,m в n-й строке m-го столбца может быть выражен как:

, для и Рав. (6)

В отличие от матриц Уолша матрицы Фурье могут быть сформированы любой квадратной размерности (например, 2, 3, 4, 5 и так далее).

Для системы N_R×3, при N_R 3, четыре примерных управляющих матрицы могут быть сформированы из матрицы Фурье, как изложено ниже:

, ,

и ,

где равна ;

получена перемножением каждой из строк 2 и 3 с -1; получена перемножением каждой из строк 2 и 3 с +j и получена перемножением строки 2 с +j.

Каждая из строк 2 и 3 может быть независимо перемножена со скаляром +1, или . Для N =3 всего 16 управляющих матриц может быть сформировано с помощью четырех скаляров. Дополнительные управляющие матрицы могут быть сформированы с помощью других скаляров, например и так далее. Множество L управляющих матриц может быть сформировано, как изложено ниже: и так далее, где масштабирование посредством имеет следствием, что каждый столбец обладает единичной энергией.

Для системы N_R, при N_R 4, четыре примерных управляющих матрицы могут быть сформированы из матрицы Уолша, как изложено ниже:

, ,

и ,

где равна ;

получена умножением каждой из строк со 2 по 4 на -1;

получена умножением каждой из строк со 2 по 4 на +j; и

получена умножением строки 2 на +j.

Каждая из строк со 2 по 4 может быть независимо перемножена со скаляром +1, -1, +j или . Для N=4 всего 64 управляющих матрицы может быть сформировано с помощью четырех скаляров. Дополнительные управляющие матрицы могут быть сформированы с помощью других скаляров, например, и так далее. Множество L управляющих матриц может быть сформировано, как изложено ниже: и так далее.

Для N=4 элементы матрицы Фурье находятся в множестве . Если строки умножаются на скаляры и , то элементы результирующих управляющих матриц также находятся в множестве . В этом случае вычисление для пространственной обработки может быть упрощено, как описано выше.

Для N=3 элементы матрицы Фурье находятся в множестве, состоящем из . Если строки умножаются на скаляры (поворот на °), (поворот на °), (поворот на °), (поворот на °), (поворот на °) и (поворот на °), то элементы результирующих матриц таковы, что, по меньшей мере, одна из составляющих находится в множестве, состоящем из {0, +1, -1, +1/2, -1/2}. Умножение для этой составляющей может быть выполнено сдвигом (если необходимо для деления на 2) и инверсией знакового разряда (если необходимо). Умножение комплекснозначного символа данных, , на элемент такой управляющей матрицы, в таком случае, потребовало бы, самое большее, одного вещественного умножения для составляющей с модулем .

Фиг. 2 показывает блок-схему последовательности 200 операций способа формирования управляющих матриц и управляющих векторов, используемых для псевдослучайного управления передачей. Сначала получают базовую матрицу (этап 212). Базовая матрица может быть матрицей Уолша, матрицей Фурье или некоторой другой унитарной матрицей, содержащей ортогональные столбцы. Матрица Уолша может упростить вычисление для PRTS, но имеет размерность, которая является степенью двойки. Матрица Фурье может быть сформирована любой размерности, и определенные размерности (например, четыре) могут обеспечивать упрощенное вычисление для PRTS.

Затем выбирается другая комбинация скаляров для новой управляющей матрицы, которая должна быть сформирована (этап 214). Первая строка базовой матрицы типично не затрагивается (или умножается на +1), а каждая из других строк может быть умножена на любой из K возможных скаляров, где, в общем, и . Выбранная комбинация может включать в себя скаляров для строк со 2 по N базовой матрицы, один скаляр на строку. K скаляров могут быть выбраны из условия, чтобы элементы результирующей матрицы имели форматы, которые могут упростить вычисление. Например, K может быть четырьмя, и четырьмя возможными скалярами могут быть +1, , +j и . Для первой управляющей матрицы комбинацией скаляров могут быть все +1. Вообще, ноль, один или более скаляров в выбранной комбинации могут быть равны +1, каковое соответствует отсутствию изменения в строке базовой матрицы, перемножаемой с этим скаляром. В любом случае новая управляющая матрица формируется посредством умножения N строк базовой матрицы на выбранную комбинацию N скаляров (этап 216). Сформированная управляющая матрица может быть сохранена в памяти или сразу использована для пространственной обработки.

Затем производится определение того, необходима или нет еще одна управляющая матрица (этап 218). Если ответом является 'да', то последовательность данных возвращается на этап 214 и выбирается другая комбинация скаляров для следующей управляющей матрицы. Если формируется множество L управляющих матриц, то используется L разных комбинаций скаляров с тем, чтобы дубликатные управляющие матрицы не формировались для множества. Если управляющие матрицы формируются «на лету», то комбинация скаляров для каждой управляющей матрицы может быть выбрана таким образом, чтобы избежать формирования дубликатных управляющих матриц, например, в пределах предопределенного количества диапазонов передачи.

Разные комбинации скаляров могут выбираться детерминированным образом, чтобы избежать дублирования. В качестве примера, для N=4 и K=4 может быть использован 3-разрядный 4-ичный счетчик, с тремя разрядами, являющимися помеченными как x, y и z. Разряд x может быть ассоциативно связан со строкой 2 базовой матрицы, разряд y может быть ассоциативно связан со строкой 3, а разряд z может быть ассоциативно связан со строкой 4. Каждый разряд имеет интервал значений от 0 до 3. Скаляр +1 может использоваться для строки 2 базовой матрицы, если x=0, скаляр -1 может использоваться, если x=1, скаляр +j может использоваться, если x=2, и скаляр -j может использоваться, если x=3. Разряды y и z подобным образом определяют, какие скаляры следует использовать, соответственно для строк 3 и 4 базовой матрицы. Счетчик может приращиваться на этапе 214 для каждой новой управляющей матрицы. Например, счетчик может отсчитывать от 000 до 003, затем от 010 до 013, затем от 020 до 023, затем от 030 до 033, затем от 100 до 103 и так далее, и, наконец, от 330 до 333. Три разряда (xyz)счетчика могли бы определять, какие скаляры следует использовать для строк со 2 по 4 базовой матрицы. Другие механизмы и схемы также могут использоваться для выбора разных комбинаций скаляров, чтобы использовать для строк базовой матрицы, чтобы формировать разные управляющие матрицы. После того, как на этапе 214 была выбрана другая комбинация скаляров, формируется еще одна управляющая матрица с использованием этой комбинации скаляров на этапе 216.

За этапом 218, если еще одна управляющая матрица не нужна (например, так как были сформированы все L управляющих матриц для множества), то может быть сформировано множество управляющих векторов, если необходимы для передачи MISO (этап 220). Управляющие векторы могут быть сформированы столбцами управляющих матриц, сформированных на этапах с 212 по 218. Затем последовательность операций завершается.

Управляющие матрицы, сформированные описанным выше образом, являются разными перестановками базовой матрицы, где перестановки определяются разными комбинациями скаляров. Скаляры выбираются обладающими единичным модулем с тем, чтобы управляющие матрицы были унитарными матрицами. Скаляры, кроме того, могут выбираться из условия, чтобы элементы управляющих матриц могли упрощать вычисление для PRTS. Элементы каждой управляющей матрицы, сформированной из матрицы Уолша или матрицы Фурье, также имеют равный модуль , что упрощает масштабирование этих элементов и обеспечивает другие преимущества.

Управляющие матрицы и управляющие векторы, используемые для псевдослучайного управления передачей, могут быть сформированы на основании базовой матрицы и сохранены в памяти. После этого одна управляющая матрица/вектор может быть выбрана для использования для каждого диапазона передачи, и выбранная управляющая матрица/вектор извлекается из памяти. В качестве альтернативы управляющие матрицы/векторы могут формироваться в реальном времени, по мере их необходимости.

Как отмечено выше, каждый управляющий вектор может рассматриваться как вырожденная управляющая матрица, содержащая только один столбец. Таким образом, в качестве используемой в материалах настоящей заявки матрица может содержать в себе единственный или многочисленные столбцы.

2.Выбор управляющей матрицы

L управляющих матриц в множестве могут выбираться для использования различными способами. В одном из вариантов осуществления управляющие матрицы выбираются из множества L управляющих матриц детерминированным образом. Например, L управляющих матриц могут циклически проходиться и выбираться в последовательном порядке, начиная с