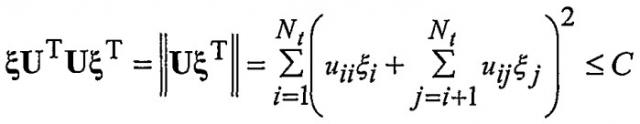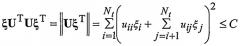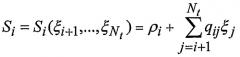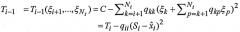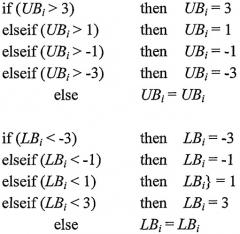Детектирование сигналов с использованием метода сферического декодирования

Детектирование сигналов с использованием метода сферического декодирования

Иллюстрации

Показать все

Реферат

Область техники

Настоящее изобретение в целом относится к детектированию сигналов. В частности, настоящее изобретение относится к детектированию сигналов с использованием методов сферического декодирования.

Описание предшествующего уровня техники

В последнее время в области систем связи метод, основанный на использовании множества входов и множества выходов (MIMO), привлек к себе большое внимание научного сообщества. Важной и интересной областью исследований MIMO-систем, и к тому же связанной с другими системами, является детектирование принятых сигналов.

Детектирование принятых сигналов относится к определению, какие сигналы были переданы, на основании принятого сигнала. С использованием векторной записи, где, в случае MIMO-системы, каждый компонент x _i вектора переданного сигнала x изображает сигнал (символ), переданный с одной MIMO-антенны, целью при декодировании сигнала является определение переданного сигнала x на основании сведений о канале и принятого сигнала r. Символ x _i должен быть действительным символом схемы модуляции, использованной при передаче. В принципе, символ схемы модуляции, появляющийся в результате канальных искажений, как наиболее близкий к принятому символу r _i, определяется как переданный символ x _i. Вычисление расстояний (меры различия) для всех возможных символов является чрезвычайно сложной задачей, поэтому, на практике, ближайший символ в пределах определенной области поиска выбирается в качестве переданного символа x _i. Трудность состоит в нахождении эффективным образом этого символа схемы модуляции, ближайшего к принятому символу r _i, или кандидатов на этот ближайший символ.

Были предложены разные алгоритмы, обсужденные и проверенные в отношении детектирования сигналов. Один из этих алгоритмов детектирования сигнала, предложенный Е. Витербо и Дж. Баутросом, назван «сферическим декодером» (E. Viterbo, J. Boutros, «A Universal Lattice Code Decoder for Fading Channels», IEEE Transactions on Information Theory, Vol.45, No.5, July 1999, pp. 1639-1642). Сферический декодер изначально представлен для декодирования кодированного сигнала, но он также применим при детектировании сигнала. Сферический декодер является квазиоптимальным методом максимального правдоподобия, имеющим преимущества в невысокой сложности. При сферическом кодировании компоненты x _i сигнала определяются один за другим поиском наиболее близкого действительного символа схемы модуляции для принятого символа r _i в пределах области поиска.

Основная идея в сферическом декодере состоит в том, чтобы обрабатывать векторы и матрицы, представляющие принятые символы и сведения о канале, так, что учитываются взаимные помехи между передаваемыми символами x ₁ ,x ₂ ,...,x _N, вызванные каналом, и в то же время можно определить первый символ x _N независимо от других символов. Используя первый определенный символ x _N, можно определить символ x _N-1 и так далее для получения в результате вектора x, содержащего символы x _i. Первый определенный символ здесь обозначен индексом N, поскольку вычисления в сферическом декодере обычно сведены с использованием верхних треугольных матриц.

Когда информация передается и искажается в канале с шумом, данные становятся нечеткими, и любое решение, принятое на стороне приемника, может приводить к ошибкам и потере информации. Гибкое детектирование имеет целью следование некоторой информации достоверности о детектированном символе и принятие «жесткого» решения в приемнике настолько поздно, насколько это возможно. Известные сферические декодеры спроектированы как детектор с «жестким» выходом, возвращающий в качестве переданного сигнала x вектор символов комбинации с кратчайшим эвклидовым расстоянием до принятого сигнала r. Кроме того, возможно, что в распоряжении имеется некоторая априорная информация, относящаяся к переданному сигналу. Эта априорная информация может повысить точность определения переданного сигнала x.

Во многих системах связи определено некоторое количество схем модуляции, которые могут быть использованы. Используемая схема модуляции может изменяться от пользователя к пользователю, например, в зависимости от скорости передачи, относящейся к каждому пользователю. Современные способы сферического детектирования не могут декодировать сигналы, относящиеся к разным схемам модуляции, одновременно.

Соответственно, есть потребность в более многофункциональных способах детектирования сигнала. Задачей настоящего изобретения является обеспечение детектирования сигнала с использованием сферического декодирования для разных назначений.

Понятно, что хотя задачи, относящиеся к детектированию сигналов с использованием сферического декодирования, описаны в связи с MIMO-системами, они также могут быть релевантными для других систем связи.

Сущность изобретения

Первый аспект настоящего изобретения относится к способу детектирования сигнала, причем упомянутый способ содержит

прием первого набора символов, представляющего сигнал, принятый в приемнике, и

оценивание второго набора символов, представляющего упомянутый сигнал, переданный передатчиком, с использованием метода сферического декодирования, при этом вычисление оценки использует, по меньшей мере, две схемы модуляции.

Второй аспект настоящего изобретения относится к способу детектирования сигнала, причем упомянутый способ содержит

прием первого набора символов, представляющего сигнал, принятый приемником,

оценивание второго набора символов, представляющего упомянутый сигнал, переданный передатчиком, с использованием метода сферического декодирования, и

определение информации достоверности, относящейся к битам, формирующим символ, для, по меньшей мере, одного символа из упомянутого второго набора.

Третий аспект настоящего изобретения относится к способу детектирования сигнала, причем упомянутый способ содержит

прием первого набора символов, представляющего сигнал, принятый приемником, и

вычисление оценки второго набора символов, изображающего упомянутый сигнал, переданный передатчиком, с использованием метода сферического декодирования, при этом информация достоверности, относящаяся к упомянутому сигналу, учитывается при оценивании, по меньшей мере, одного символа из второго набора.

Четвертый аспект настоящего изобретения относится к устройству для детектирования сигнала, причем упомянутое устройство выполнено с возможностью

приема первого набора символов, представляющего сигнал, принятый антенной приемника, и

оценивания второго набора символов, представляющего упомянутый сигнал, переданный передатчиком, с использованием метода сферического декодирования, при этом оценивание использует, по меньшей мере, две схемы модуляции.

Пятый аспект настоящего изобретения относится к устройству для детектирования сигнала, причем упомянутое устройство выполнено с возможностью

приема первого набора символов, изображающего сигнал, принятый антенной приемника, и

оценивания второго набора символов, представляющего упомянутый сигнал, переданный передатчиком, с использованием метода сферического декодирования, и

определения информации достоверности, относящейся к битам, формирующим символ, для, по меньшей мере, одного символа из упомянутого второго набора.

Шестой аспект настоящего изобретения относится к устройству для детектирования сигнала, причем упомянутое устройство выполнено с возможностью

приема первого набора символов, представляющего сигнал, принятый антенной приемника, и

оценивания второго набора символов, представляющего упомянутый сигнал, переданный передатчиком, с использованием метода сферического декодирования, при этом информация достоверности, относящаяся к упомянутому сигналу, учитывается при оценивании, по меньшей мере, одного символа из второго набора.

Седьмой аспект настоящего изобретения относится к системе для детектирования сигнала, причем система содержит

средство приема для приема первого набора символов, представляющего сигнал, принятый приемником; и

средство оценивания для оценивания второго набора символов, представляющего упомянутый сигнал, переданный передатчиком, с использованием метода сферического декодирования, при этом средство оценки использует, по меньшей мере, две схемы модуляции.

Восьмой аспект настоящего изобретения относится к системе для детектирования сигнала, причем система содержит

средство приема для приема первого набора символов, представляющего сигнал, принятый приемником;

средство оценивания для оценивания второго набора символов, представляющего упомянутый сигнал, переданный передатчиком, с использованием метода сферического декодирования; и

средство определения для определения информации достоверности, относящейся к битам, формирующим символ, для, по меньшей мере, одного символа из упомянутого второго набора символов.

Девятый аспект настоящего изобретения относится к системе для детектирования сигнала, причем система содержит

средство приема для приема первого набора символов, представляющего сигнал, принятый приемником; и

средство оценивания для оценивания второго набора символов, представляющего упомянутый сигнал, переданный передатчиком, с использованием метода сферического декодирования, при этом информация достоверности, относящаяся к упомянутому сигналу, учитывается при оценивании, по меньшей мере, одного символа из второго набора символов.

Краткое описание чертежей

Варианты осуществления настоящего изобретения далее описаны, только в качестве примера, со ссылкой на чертежи, на которых показано следующее:

фиг.1 - схематичное представление системы связи MIMO, в которой могут быть использованы варианты осуществления изобретения,

фиг.2 - графическое представление принципа сферического декодера для детектирования сигнала,

фиг.3А - упрощенная блок-схема алгоритма сферического декодера для детектирования сигнала в соответствии с вариантом осуществления изобретения,

фиг.3В - упрощенная блок-схема алгоритма сферического декодера для детектирования сигнала в соответствии с первым вариантом осуществления изобретения,

фиг.3С - упрощенная блок-схема алгоритма сферического декодера для детектирования сигнала в соответствии со вторым вариантом осуществления изобретения,

фиг.3D - упрощенная блок-схема алгоритма сферического декодера для детектирования сигнала в соответствии с третьим вариантом осуществления изобретения,

фиг.4 - схематичное представление сферического декодера и устройства для детектирования сигнала в соответствии с вариантом осуществления изобретения,

фиг.5 - блок-схема алгоритма смешанного сферического 4-QAM/16-QAM-декодера для детектирования сигнала в соответствии с первым вариантом осуществления изобретения,

фиг.6 - 4-QAM-комбинация с отображением Грея, показывающим расстояние от принятой точки до ближайших точек комбинации, где первым битом является 0 и 1,

фиг.7 - иллюстрация формирования правдоподобия бита принятого символа r ₁ в 4-QAM-системе с одной антенной передатчика/приемника,

фиг.8 - 16-QAM-комбинация с отображением Грея, которая использована в качестве примера,

фиг.9 - этапы получения расстояний d ₀ и d ₁ для первого бита принятого символа r ₁ в 16-QAM-системе с одной антенной передатчика/приемника,

фиг.10 - блок-схема алгоритма сферического 16-QAM-декодера с гибким выходом для детектирования сигнала в соответствии со вторым вариантом осуществления изобретения,

фиг.11 - взвешенные кандидаты для сферического декодера с дополнительным гибким входом для 4-QAM-системы в соответствии с третьим вариантом осуществления изобретения,

фиг.12 - взвешенные кандидаты для сферического декодера с дополнительным гибким входом для 16-QAM-системы в соответствии с третьим вариантом осуществления изобретения,

фиг.13А - первая часть блок-схемы алгоритма для сферического 16-QAM-декодера с дополнительным гибким входом для детектирования сигнала в соответствии со вторым вариантом осуществления изобретения и

фиг.13В - вторая часть блок-схемы алгоритма по фиг.13А.

Подробное описание предпочтительных вариантов осуществления

В последующем описании делаются ссылки на систему с множеством входов и множеством выходов (MIMO). Настоящее изобретение, однако, не ограничено декодированием сигналов MIMO-системы. Ниже описаны другие системы, где может применяться настоящее изобретение.

В последующем описании делаются ссылки на сферический декодер для обеспечения согласованности с исходным сферическим декодером. Однако понятно, что при описании детектирования сигнала с использованием сферического декодера акцент делается на детектировании сигнала, и не предполагает наличия какого-либо кодирования в принятом сигнале. Информация, переносимая принятым сигналом, может быть кодированной или некодированной.

На фиг.1 показано схематичное представление системы связи MIMO в качестве примера системы связи, где могут быть использованы варианты осуществления изобретения. Система связи MIMO по фиг.1 содержит передающую антенную решетку, содержащую N _t передающих антенн, и приемную антенную решетку, содержащую N _r приемных антенн. В последующем принимается во внимание ограничительное условие N _t = N _r симметрии. Вектор, передаваемый в течение каждого периода времени, обозначен как x = [x ₁,x ₂,...,x _N], где каждый компонент является независимым вариантом выбора, например, из смешанной комбинации M-QAM (квадратурной амплитудной модуляции). Переданный сигнал формируется как x = vL, где L - матрица генератора решетки с базисом {m₁,m₂,...,m_n}, а v = {ν₁,ν₂,...,} - вектор целочисленных компонентов, на который отображены информационные биты.

Принятый сигнал изображен посредством r = Hx + n, где матрица H - матрица канала, а n представляет шумы. В связи с MIMO-системой матрица H канала представляет каналы системы с множеством входов и множеством выходов, а x _i изображает символ, переданный одной из антенн системы с множеством входов и множеством выходов. В связи с системой с временным разделением матрица H представляет множество путей от передающей антенны к приемной антенне, а компоненты x _i представляют последовательные символы пользователя системы с временным разделением. В связи с системой с кодовым разделением матрица H представляет разные коды системы с кодовым разделением или любую блочную матрицу передачи, а x _i представляет сигнал, относящийся к одному из разных кодов.

Понятно, что, в общем случае, сферическое декодирование может быть использовано для детектирования сигнала при наличии взаимных помех, где взаимные помехи могут происходить из произвольного источника, как в примерах, приведенных выше.

Целью детектора со сферическим декодером является нахождение действительных точек комбинации (решетки Λ) внутри сферы или радиуса , центрированных в принятой точке, на основе метрики

(1)

где r = Hx + n - принятый вектор, а решеткой Λ является результат линейного преобразования, определенного матрицей в применении к кубической решетке . Этот принцип графически иллюстрируется на фиг.2.

Для декодирования сигнала решаемая задача, следовательно, заключается в том, чтобы найти кратчайшее расстояние в «преобразованной» решетке такое, что

(2)

где w определено как w = ξ L, при , и r = ρL при , имея в виду, что ρ и ξ - действительные векторы. Видно, что

,

где ξ _i = ρ _i - ν _i, i = 1,...,N _t, определяют преобразованные оси координат.

С помощью этого преобразования оси сфера преобразуется в эллипсоид, центрированный в начале новой системы координат, определенной по ξ, и

(3)

С использованием, например, разложения Холецкого матрица H раскладывается на новую верхнюю диагональную матрицу U, такую что U ^T U = HH ^T, a уравнение (3) может быть переписано как

(4)

которое, после подстановки и , имеет вид:

(5)

Применяя алгоритм, описанный Баутросом и Витербо в статье, упомянутой выше, можно использовать принятую точку с индексом i = N _t, чтобы найти с индексом N _t - 1 и так далее, получая следующие уравнения для верхнего и нижнего граничных значений составляющей :

(6)

где

(7)

и

(8)

Во время итераций граничные значения, определенные по уравнениям (7) и (8), обновляются рекурсивно с использованием уравнений

(9)

и

(10)

При выполнении этих итераций могут иметь место два случая:

а) декодер доходит до и выбирает значение в пределах вычисленного диапазона. В этом случае, если расстояние детектированного набора символов из принятой точки, заданное согласно

не больше, чем C, то поиск завершается, и возвращается вектор , в ином случае последовательность операций должна начаться снова с бóльшим радиусом сферы;

b) декодер не находит в комбинации точку, которая лежит между верхним и нижним граничными значениями для . В этом случае декодер должен вернуться обратно к использовать другое значение-кандидат в пределах верхнего и нижнего граничных значений, и снова совершить попытку относительно . Если больше не имеет кандидатов, декодер возвращается к и так далее.

Понятно, что, хотя выше упоминается определение символов один за другим, можно определять символы в группах с использованием разных методов матричной обработки.

Алгоритм сферического декодера может быть модифицирован для уменьшения сложности при поиске наилучшей точки внутри сферы. Исходный сферический декодер начинает поиск на поверхности сферы и зигзагообразно перемещается в направлении центра, отыскивая ближайшую точку решетки к принятой точке. В противоположность этому, алгоритм уменьшенной сложности (C.P. Schnorr, M. Euchner, «Lattice basis reduction: improved practical algorithms and solving subset sum problems», Mathematical Programming, Vol.66, 1994, pp. 181-191) предлагает начинать поиск от центра сферы и двигаться наружу. Как только действительная точка решетки найдена внутри сферы, ее радиус уменьшается до расстояния вновь обнаруженной точки решетки от центра, и поиск переходит к следующей точке. Кроме того, описан сокращенный сферический декодер (A.M. Chan и I. Lee, «A New Reduced-Complexity Sphere Decoder For Multiple Antenna Systems», IEEE International conference on Communications ICC'02, Vol.1, No.28, May 2002, pp. 460-464).

Можно предположить, что при перемещении из центра сферы сферический декодер будет находить ближайший символ за меньшее количество операций, чем при начале движения от границы. Для уменьшения сложности сферического декодера должны быть приняты во внимание два главных дополнения к исходному сферическому декодеру. Сначала, для каждого нижнего и верхнего граничного значения i-ой координаты, символы кандидатов в их пределах сортируются в порядке по возрастанию согласно метрике и сохраняются в векторе z _i.

Здесь y _i - вектор с элементами [y _i,1,y _i,2,...], содержащий все точки комбинации между LB _i и UB _i. Это вынуждает алгоритм осуществлять поиск координат, ближайших к середине интервала, определенного граничными значениями, вместо поиска координат сначала около нижнего граничного значения. Во вторых, каждый раз, когда точка решетки находится в пределах сферы, вектор T в уравнении (10) и все нижние и верхние граничные значения в уравнениях (7) и (8) обновляются. Эти обновления исключают некоторые из координат кандидатов на самых правых краях вектора z _i путем сокращения длины возможных символов. Как показано на фиг.5, вектор z _i содержит отсортированные компоненты вектора y _i и вектор ρ, который является принятым сигналом с инвертированным каналом. Остаток алгоритма остается неизменным, а итерации продолжаются до тех пор, пока набор символов не будет сохранен в . Варианты осуществления настоящего изобретения могут использовать принцип сферического декодера уменьшенной сложности.

Фиг.3А показывает упрощенную блок-схему алгоритма способа детектирования сигнала сферического декодера в соответствии с вариантом осуществления изобретения. Для простоты рассмотрен симметричный случай, где количество антенн приемника и передатчика равно N _t. Кроме того, допускается, что переданные и принятые сигналы должны иметь действительные значения, и показаны только главные признаки итеративного определения переданных символов x _i. На этапе 301 счетчик i инициализирован значением N _t. Символ x _i определяется на этапе 302 способом, обсужденным выше, с использованием, например, соответствующих этапов сферического декодера уменьшенной сложности или этапов исходного сферического декодера. Этап 302 содержит два подэтапа. На этапе 302а при определении символа x _i учитывается модуляция переданного символа x _i. На этапе 302b при определении переданного символа x _i учитывается априорная информация. После того как символ x _i определен, значение счетчика проверяется на этапе 303. Если были определены не все символы x _i, значение счетчика декрементируется на этапе 304, и способ продолжает определять следующий символ x _i-1. Если все символы x _i были определены, вектор x выводится на этапе 305. На этапе 306 для вектора x определяется информация достоверности, относящаяся к битам, формирующим символы.

На фиг.3А этап 302а предоставляет возможность детектирования символов x _i разных схем модуляции. Схема модуляции x _i обычно влияет на область поиска для символа x _i. Этап 302b позволяет учитывать гибкую априорную информацию. Эта априорная информация обычно используется при задании весов символам-кандидатам в пределах области поиска. Априорная информация относительно, по меньшей мере, некоторых информационных бит или символов может быть любой информацией достоверности, относящейся к переданному или принятому сигналу. Она может быть получена, например, из декодера канала или детектора ошибок, следующих за детектором со сферическим декодером, или из предыдущих продетектированных символов в детекторе со сферическим декодером. Другие примеры включают в себя априорную информацию из любого внешнего источника, такого как декодер канала или детектор ошибок других информационных потоков, принадлежащих другому пользователю или службе.

Вектор x на этапе 305 в типовом случае является жестким выходным сигналом в том смысле, что хотя гибкая априорная информация может использоваться на этапе 302, выходной сигнал содержит только набор символов x _i. На этапе 306, в свою очередь, по меньшей мере, для одного символа, но обычно для всех символов x _i, определяется информация достоверности, относящаяся к битам, формирующим символы. Эта информация достоверности, относящаяся к битам, формирующим символы, может быть использована для вычисления гибкой информации для символов, если требуется.

Понятно, что альтернативой блок-схеме алгоритма, показанной на фиг.3А, является реализация этапа 306 в рамках этапа 302. Это означает, что гибкое значение для символа x _i определяется перед определением следующего символа x _i-1. В этом случае математические операции, относящиеся к этапам 302b и 306, в обычном случае выполняются вместе.

Возможно, что только один из этапов 302a, 302b и 306 присутствует в способе 300. Эти примеры иллюстрируются на фиг.3B, 3C и 3D, которые показывают блок-схемы алгоритмов для способов 310, 320 и 330. В качестве альтернативы, могут быть представлены любые два из этих этапов. Кроме того, как показывает фиг.3А, все этапы 302a, 302b и 306 могут быть представлены в способе 300.

Три варианта осуществления изобретения описаны ниже более подробно. Первый вариант осуществления изобретения относится к одновременному детектированию символов разных схем модуляции. Сферический декодер для детектирования сигнала в соответствии с первым вариантом осуществления здесь назван смешанным сферическим декодером для детектирования сигнала. Второй вариант осуществления изобретения относится к получению гибких значений на выходе сферического декодера. Сферический декодер для детектирования сигнала в соответствии со вторым вариантом осуществления здесь назван сферическим декодером с гибким выходом для детектирования сигнала. Третий вариант осуществления изобретения направлен на прием дополнительной гибкой априорной информации, в типовом случае, в виде вероятностей. Сферический декодер для детектирования сигнала в соответствии с третьим вариантом осуществления здесь назван сферическим декодером с дополнительным гибким входом для детектирования сигнала.

Фиг.4 схематично показывает сферический декодер 404 для детектирования сигнала и устройство 400 в соответствии с вариантом осуществления изобретения. Устройство 400 содержит, в качестве примера, набор антенн 401a, 401b и 401c. В качестве примера, это устройство 400 относится к системам с расширенным спектром. Каждая антенна 401 присоединена к блоку 402 радиочастотной обработки (РЧ)/сжатия. Блоки 402 РЧ/сжатия присоединены к блоку 403 оценки канала, который обеспечивает определение матрицы H канала и принятых символов r. Из блока 403 оценки канала информация о принятых символах и о свойствах канала направляется в сферический декодер 404 для детектирования сигнала. Сферический декодер 404 для детектирования сигнала может быть смешанным сферическим декодером, сферическим декодером с дополнительным гибким входом и/или сферическим декодером с гибким выходом. Выход сферического декодера 404 присоединен к декодеру 405 кода канала. В качестве одного из примеров источника априорной информации фиг.4 показывает, как информация из декодера 405 кода канала направляется обратно в сферический детектор 404 для детектирования сигнала.

Сферический декодер 404 для детектирования сигнала может быть реализован в виде подходящего программного кода для программируемого процессора. В качестве альтернативы, декодер 400 может быть реализован в виде аппаратных средств, специально спроектированных для сферического декодирования.

Устройство 400 может быть портативным устройством связи. Оно может быть, например, абонентской аппаратурой, мобильным телефоном, мобильной станцией, персональным цифровым секретарем или «дорожным» компьютером. Устройство 400, в качестве альтернативы, может быть стационарным устройством. Кроме того, устройство 400 может быть сетевым элементом для сети связи. Оно может быть, например, сетевым элементом приемопередатчика для системы сотовой связи.

Понятно, что РЧ-секция приемника образована блоками 402 РЧ/сжатия. Секция базовой полосы приемника образована блоком 403 оценки канала, детектором 404 сигнала, использующим сферический декодер, и декодером 405 кода канала. Секция базовой полосы приемника необязательно должна содержать декодер 405 кода канала, но в типовом случае сигналы, передаваемые через радиоинтерфейс, являются канально-кодированными.

Первый вариант осуществления изобретения относится к одновременному детектированию символов разных схем модуляции. В качестве примера рассмотрен смешанный сферический декодер с N _t передающими антеннами и N _r = N _t приемными антеннами, обеспечивающий детектирование символов 4-QAM и 16-QAM, передаваемых одновременно разными антеннами.

Понятно, что, хотя этот отдельный пример относится к детектированию символов, переданных с использованием разных известных схем модуляции или алфавитов модуляции, возможно, что приемник не имеет информации о схеме модуляции, использованной для символа. Приемник может пытаться детектировать символ с использованием некоторого количества возможных алфавитов модуляции, а затем выбирать корректный алфавит модуляции с использованием некоторых предопределенных критериев.

Известные алгоритмы сферического декодирования действительны только для детектирования сигнала с действительными комбинациями. Чтобы использовать сферическое декодирование для детектирования сигналов с комплексными комбинациями, входящий вектор r и матрица H канала должны быть разложены на действительные и мнимые части перед их использованием в сферическом декодере. Эти разложения показаны ниже:

и

r ^dagger и H ^dagger будут использованы в описании, опуская символ «dagger». Значение 2N _t также будет использовано для обозначения длины r ^dagger.

Во время итераций сферического декодера возможные значения, которые может принимать , заданы граничными значениями, установленными в уравнении (6). Эти граничные значения должны быть принудительно применены к значениям комбинации.

В случае 4-QAM комбинация может быть описана вектором L _4QAM = [-1,1], и поэтому варианты выбора для точки выбираются с максимальным или минимальным значением между граничными значениями, а точки решетки - как LB _i = max(LB _i,-1) и UB _i = max(UB _i,1), где LB _i и UB _i сначала вычисляются как в уравнениях (7) и (8).

Во второй рассматриваемой схеме, 16-QAM, комбинация может содержать значения L _16QAM = [-3,-1,1,3], создавая ситуацию, в которой более сложная точка-кандидат теперь лежит в пределах любой пары соседних точек комбинации. Для того, чтобы получить корректные граничные значения, необходим ряд условий, проверяющих каждую точку комбинации. Этот набор условий выражен в кодах MATLAB, изложенных ниже, где LB _i и UB _i изначально вычислены, как в уравнениях (7) и (8).

В дополнение к граничным условиям, выведенным ранее, также целесообразно определять новую векторную схему = [sch ₁,sch ₂,...,], значения которой будут содержать способ модуляции, используемый в каждой передающей антенне (например, 1 - для 4-QAM и 2 - для 16-QAM). Так, сферический декодер может детектировать символы из комбинаций 4-QAM и 16-QAM, передаваемых на разных антеннах.

Как описано ранее, алгоритм сферического декодера будет начинать поиск с принятого символа 2N _t, двигаться в обратном направлении к 2N _t - 1 и так далее. Смешанное детектирование попросту требует, чтобы для каждого символа i использовался соответствующий набор сравнений в зависимости от значения sch _i. Таким образом, объем поиска сферического декодера настраивается на основании (известной или предполагаемой) модуляции .

При этих условиях алгоритм смешанного сферического 4-QAM/16-QAM-декодера формируется, как показано на фиг.5, где либо вектор L _4QAM, либо вектор L _16QAM должен использоваться при вычислении LB _i и UB _i. На фиг.5 символ enum( ) обозначает набор кандидатов i-ого символа, заданный верхним и нижним пределами ; символ length( ) задает количество символов, содержащихся в этом наборе, удерживая значение в пределах N _i; и символ sort( ) сортирует набор в возрастающем порядке согласно с выходными значениями, сохраненными в векторе z _i.

На этапе 501 переменная ntx установлена равной количеству столбцов верхней диагональной матрицы U (другими словами, в 2N _t). На этапе 501 значение для q _ii и q _ij также устанавливаются, как описано выше в связи с уравнением (5). На этапе 502 инициализируются T_ntx, dbest и S. На этапе 503 переменная ix, которая соответствует индексу i, инициализируется как равная количеству столбцов верхней диагональной матрицы U. Этапы с 504 по 511 относятся к нахождению действительной точки решетки в качестве кандидата для . Точки решетки в пределах диапазона поиска LB_ix и UB_ix сохраняются в векторе z _ix длиной в N_ix. N_ix - некоторое количество найденных точек решетки в пределах диапазона поиска, X_ix - индекс в пределах вектора z _ix, а элементы в пределах z _ix отсортированы согласно тому, насколько они близки к центру сферы. На этапе 504 верхний предел UB_ix и нижний предел LB_ix вычисляются в соответствии с уравнениями (7) и (8). Векторы y _ix и z _ix, а также индекс X_ix на этапе 504 относятся к алгоритму сферического декодера уменьшенной сложности, как описано выше. Индекс X_ix инициализируется в нуль на этапе 504 и увеличивается на единицу на этапе 505, чтобы начать поиск от центра сферы. Этап 506 относится к удержанию поиска в пределах сферы поиска. На этапе 507 проверяется, все ли символы для точки решетки были определены. Если нет, выполняются этапы с 508 по 511, а этапы с 504 по 507 повторяются. Этапы 508 и 509 относятся к уравнениям (9) и (10). На этапе 510 счетчик обновляется; этот счетчик относится к подсчитыванию количества итераций в пределах алгоритма сферического декодера. На этапе 511 переменная ix уменьшается, так что в следующем цикле этапы с 504 по 509 относятся к следующему принятому символу 2N _t - 1.

Как только действительная точка решетки найдена, алгоритм продолжается до этапа 512, где определяется квадратичное расстояние между найденной точкой решетки и принятой точкой. Если квадратичное расстояние для самой последней найденной точки решетки является меньшим, чем для более ранних найденных точек решетки (этап 513), то алгоритм переходит к этапу 514. На этапе 514 радиус сферы уменьшается, верхнее и нижнее граничные значения обновляются, а найденная точка решетки сохраняется в векторе в соответствии с алгоритмом сферического декодера уменьшенной сложности. Алгоритм затем продолжается на этапе 515 для нахождения следующей действительной точки р