Оптимизация последовательных комбинаторных процессов

Оптимизация последовательных комбинаторных процессов

Иллюстрации

Показать все

Реферат

Предпосылки создания изобретения

Настоящее изобретение относится к оптимизации последовательных (многостадийных) комбинаторных процессов.

Известно множество примеров процессов, заключающихся в осуществлении ряда стадий, при этом конечный результат таких процессов может быть оптимизирован за счет реализации этих стадий предпочтительным образом. Производственные процессы, например, могут состоять из стадий, на которых на качество производимой продукции влияют такие конкретные переменные величины, как размер, количество, длительность, давление, температура, вязкость и т.д. Поскольку промышленность, естественно, заинтересована в обеспечении высокого качества, часто желательно оптимизировать различные стадии, чтобы получить наилучший конечный результат.

Такую оптимизацию часто осуществляют путем моделирования процесса. Таким образом сравнивают различные значения параметра или группы параметров, чтобы установить, какие из них обеспечивают лучший результат. Одной из методик моделирования, которая представляет особый интерес ввиду ее высокой точности и способности справляться со сложными сценариями, является анализ методом конечных элементов. Применительно к процессу рассматриваемого типа данная модель в целом учитывает интересующие параметры как описываемые в непрерывном числовом пространстве, в котором параметры могут иметь любое значение, и ищет оптимальное значение каждого из них с учетом остальных параметров. Вместе с тем, с точки зрения необходимого для вычислений времени такое решение является дорогостоящим. Один "прогон" модели на основе метода конечных элементов для одного набора величин параметров может занять несколько часов, при этом обычно существует множество величин, требующих анализа. Это означает, что модели потребуются тысячи последовательных приближений, чтобы прийти к какому-либо оптимальному решению, в результате чего полный анализ процесса может занять неосуществимо долгое время. Связанные с ним расходы могут перевесить любые преимущества, достигнутые за счет оптимизации процесса.

Данный недостаток был преодолен за счет так называемой имитации моделирования (surrogate modelling). Идея использования имитаций моделей при оптимизации широко исследована применительно к проблемам, связанным с обширными вычислениями. Имитация является простым приближением модели на основе метода конечных элементов (или другой сложной модели) к менее длительным итерационным процессам, что ускоряет вычисления. Хорошо известной имитацией модели является криджинг, но также может использоваться любой другой метод последовательных приближений, применимый к конкретной задаче. Результаты нескольких прогонов модели анализа методом конечных элементов вводят в имитацию модели для ее "обучения". Количество таких прогонов зависит от сложности анализируемого процесса; как правило, 20-30 прогонов достаточно для обеспечения достаточного уровня точности. После завершения обучения имитации модели ее пропускают через цикл оптимизации, в ходе которого она вычисляет результат процесса при всех возможных значениях интересующего параметра или параметров и выдает значение, которое соответствует оптимальному результату процесса. Однако данное оптимальное значение основано на последовательных приближениях имитации модели и может быть неточным. В связи с этим применительно к тем же значениям параметров обычно прогоняют модель на основе метода конечных элементов и сравнивают результат с результатом, полученным при помощи имитации модели. В случае значительной разницы между ними результат такого последнего прогона модели на основе метода конечных элементов затем загружают в имитацию модели, чтобы усовершенствовать ее обучение, и снова пропускают имитации модели через цикл оптимизации и так далее до тех пор, пока не будет обеспечено приемлемое соответствие результатов двух моделей. За этот счет повышается точность имитации модели в оптимальной области, поскольку точность повышается там и тогда, когда это необходимо. Общее время на вычисления, которое требуется для получения оптимального значения, сокращается за счет переноса основной вычислительной нагрузки из медленной модели на основе метода конечных элементов в более быструю имитацию модели. Например, один прогон модели на основе метода конечных элементов занимает около 48 часов, тогда как для осуществления 50000 имитаций вычислений достаточно менее 10 минут.

Кроме того, точность может быть повышена за счет тщательного выбора начальных прогонов модели на основе метода конечных элементов с тем, чтобы охватить диапазон значений параметров, в который входят значения, считающиеся предположительно важными для определения оптимального значения. Данное решение известно как "планирование экспериментов" (DoE - сокращение от англ. "design of experiments"), которое позволяет избежать потенциальной непроизводительной траты времени на вычисления в процессе сценариев моделирования, результаты которых далеки от желаемых. Примером процесса моделирования с применением анализа методом конечных элементов в сочетании с планированием экспериментов является патент США US 6349467 [1], в котором описана методика оптимизации стадий производства отражателей для камер сгорания газотурбинных двигателей во избежание нежелательного промежуточного термического воздействия на листовой металл, из которого изготавливают отражатели.

До настоящего времени дополненное имитацией модели моделирование методом конечных элементов широко применялось для решения разнообразных задач, требующих оптимизации численного значения одного или нескольких параметров, применяемых в процессе. Круг таких задач был ограничен задачами, позволявшими решать их путем последовательного приближения с использованием функции имитации модели, зависящей от переменных величин непрерывного или дискретного характера, и выражать результат физическими или количественными параметрами. Вместе с тем, дополнительно существует множество процессов, которым может пойти на пользу оптимизация, но к которым неприменимы известные методы имитации моделирования, поскольку задача не заключается в поиске оптимального численного значения какого-либо параметра. К таким процессам относятся процессы, состоящие из нескольких стадий или действий, которые с целью достижения конечного результата процесса осуществляют или сочетают в любом порядке или последовательности. Однако качество конечного результата зависит от порядка, в котором осуществляют стадии. Иными словами, в комбинаторной области не существует доступных методик оптимизации имитации моделирования, в которых переменные величины не имеют физического смысла. Задача состоит в том, чтобы определить оптимальный порядок следования действий и получить наилучший результат. Следовательно, данную задачу можно охарактеризовать как задачу оптимизации последовательных комбинаторных процессов, которая заключается в идентификации последовательности, в которой следует сочетать действия, чтобы получить оптимальный результат. Очевидно, что данная задача отличается от задачи определения оптимального значения количественно измеримого параметра; отдельные действия и порядок их следования являются нечисловыми элементами, не имеющими физического смысла. До настоящего времени при решении задач оптимизации такого рода приходилось по большей части полагаться на данные полного анализа методом конечных элементов.

В основу настоящего изобретения положена задача обеспечения усовершенствованного способа оптимизации последовательных комбинаторных процессов, что может принести значительную пользу.

Краткое изложение сущности изобретения

Соответственно, согласно первой особенности настоящего изобретения предложен способ оптимизации последовательного комбинаторного процесса, состоящего из множества взаимозаменяемых действий (событий), осуществляемых в любой из множества последовательностей с целью достижения конечного результата процесса, характеризуемого рабочим параметром, заключающийся в том, что используют планирование экспериментов, включающее группу последовательностей, выбранных из множества последовательностей, при этом каждая последовательность, входящая в планирование экспериментов, связана с данными, касающимися значения вклада каждого действия из каждой последовательности в достижение конечного результата, описанного рабочим параметром; используют имитацию модели процесса, в которую в качестве исходных данных вводят последовательность действий и определяют значение конечного результата путем суммирования вкладов в конечный результат каждого действия из каждой введенной последовательности, при этом значение вклада выбирают из значений вклада, которые содержатся в данных о рабочих параметрах, согласно алгоритму, при помощи которого в планировании экспериментов осуществляют поиск соответствия между каждым действием из введенной последовательности и действиями из последовательностей планирования экспериментов согласно указателю приоритетов условий совпадения и извлекают значения вклада совпавшего действия; осуществляют прогон группы из множества последовательностей через имитацию модели и регистрируют значение конечного результата каждой последовательности; и идентифицируют оптимальную последовательность путем поиска зарегистрированных оптимальных значений конечного результата в имитации модели с целью обнаружения зарегистрированного оптимального значения рабочего параметра, при этом последовательность, которая обеспечивает такое зарегистрированное оптимальное значение, является оптимальной последовательностью.

Таким образом, имитацию модели применяют в изобретении для оптимизации последовательных комбинаторных задач, решение которых в ином случае осуществимо путем сложного моделирования, такого как моделирование методом конечных элементов. В изобретении предложено быстрое и эффективное решение задачи сложного моделирования, требующей значительных затрат времени, частично благодаря тому, что изобретение позволяет извлекать полезную информацию из имеющейся в наличии информации за счет осуществления доступа к информации согласно указателю приоритетов, основанному на ее полезности. Это дает возможность использовать более точную информацию, по возможности отдавая ей предпочтение перед менее точной информацией, и при помощи имитации модели быстро получать конечный результат, который является достаточно приближенным к более точным результатам, которые не так быстро могут быть получены при помощи обычных сложных моделей.

Таким образом, значительно сокращаются расходы на вычисления без значительной потери точности. Планирование экспериментов может быть реализовано гибко, чтобы адаптировать способ к растущим объемам информации, с возможностью динамического расширения по мере появления новых доступных данных, повышающих точность.

Способ был применен в реальной инженерно-технической практике и широко продемонстрировал свои преимущества, позволив оптимизировать технологию сварки по результатам всего 27 прогонов эталонной модели анализа методом конечных элементов из возможных 46080 комбинаций.

В некоторых вариантах осуществления способа дополнительно получают данные, связанные с каждой последовательностью из планирования экспериментов, для чего осуществляют прогон каждой последовательности из планирования экспериментов через эталонную модель процесса, в которую в качестве исходных данных введена последовательность действий и которая определяет значение конечного результата и вклад в конечный результат каждого действия из введенной последовательности.

За счет такого применения эталонной модели с высокой точностью обеспечивают информацию, необходимую имитации модели, без необходимости практического осуществления процесса. Однако глобальная оптимизация все же может быть значительно быстрее, чем оптимизация с использованием только эталонной модели, поскольку процедура проверки соответствия по приоритетам позволяет наилучшим образом использовать небольшое количество информации. Так, достаточно точные результаты получают даже в случае небольшого числа прогонов сложной эталонной модели вместо требующей больших затрат времени полной серии прогонов, которая потребовалась бы в случае применения только эталонной модели. Значительная доля затрат вычислительных ресурсов может быть перенесена на имитацию модели, что значительно ускоряет оптимизацию.

Таким образом, способ дополнительно заключается в том, что эталонную модель строят перед осуществлением прогона каждой последовательности из планирования экспериментов через такую эталонную модель. Таким образом, получают и применяют специально рассчитанную на соответствующий процесс эталонную модель, которая повышает точность.

Предпочтительно, имитация модели представляет собой упрощенное приближение к эталонной модели. Чтобы лучше использовать перенос затрат вычислительных ресурсов с эталонной модели на имитацию модели, имитация модели должна быть максимально простой, насколько это позволяет точность, поскольку расчет простой модели обычно занимает меньше времени.

Способ может дополнительно включать стадию, в которой после идентификации оптимальной последовательности осуществляют прогон идентифицированной оптимальной последовательности через эталонную модель с целью определения значения конечного результата и сравнивают зарегистрированное оптимальное значение идентифицированной оптимальной последовательности, определенное при помощи имитации модели, с конечным результатом, определенным при помощи эталонной модели, с целью проверки точности идентификации оптимальной последовательности. Поскольку эталонная модель отличается более высокой точностью, чем имитация модели, при наличии времени целесообразно осуществить прогон идентифицированной оптимальной последовательности через эталонную модель, чтобы проверить согласованность двух моделей. Согласованность является хорошим показателем того, что идентифицированная последовательность действительно является оптимальной. Затем ее с высокой степенью надежности применяют для оптимизации процесса. Кроме того, при обнаружении неприемлемого расхождения между двумя результатами дополнительный прогон через эталонную модель не является лишним, поскольку это делает доступной новую точную информацию, которой может быть дополнено планирование экспериментов, чтобы повысить точность будущих прогонов имитации модели. Таким образом, в способе дополнительно при обнаружении различия между зарегистрированным оптимальным значением идентифицированной оптимальной последовательности, определенным при помощи имитации модели, и конечным результатом, определенным при помощи эталонной модели, величина которого неприемлема для процесса, дополняют планирование экспериментов идентифицированной оптимальной последовательностью, чтобы данная последовательность и значения вкладов в конечный результат каждого действия, определенные путем прогона идентифицированной оптимальной последовательности через эталонную модель, были доступны для поиска и извлечения при помощи алгоритма имитации модели; осуществляют прогон группы из множества последовательностей через имитацию модели с целью получения новых значений конечного результата каждой последовательности; и на основании новых конечных результатов идентифицируют новую оптимальную последовательность.

Описанные в предыдущем абзаце стадии могут быть осуществлены повторно применительно к новой идентифицированной оптимальной последовательности до тех пор, пока различие между зарегистрированным оптимальным значением идентифицированной оптимальной последовательности, полученным при помощи имитации модели, и конечным результатом, полученным при помощи эталонной модели, не станет приемлемым для процесса. Такое циклическое выполнение позволяет обеспечить схождение имитации модели с точным результатом за счет того, что в имитации модели используют все большие количества содержащейся в эталонной модели точной информации, о которой известно, что она способствует оптимальному осуществлению процесса, поскольку была идентифицирована имитацией модели. Таким образом, многократное повторение является эффективным и повышающим точность.

В альтернативных вариантах осуществления способа осуществляют последовательный комбинаторный процесс с использованием каждой из последовательностей из планирования экспериментов для получения данных, связанных с каждой последовательностью из планирования экспериментов, и регистрируют значения вклада в конечный результат каждого действия из каждой последовательности. Данный подход, согласно которому для получения информации, используемой имитацией модели, применяют реальные экспериментальные данные, при некоторых обстоятельствах является предпочтительным по сравнению с более абстрактными подходами. Например, в случае простого процесса быстрее и/или дешевле осуществить процесс несколько раз применительно к различным последовательностям, чем строить сложную эталонную модель или иным образом получать информацию путем вычислений. При этом обеспечивается более высокая точность, чем в случае применения других методов, таких как адаптация данных, полученных при помощи или вычисленных для родственного процесса. Точность, которую обеспечивает данный вариант осуществления, частично зависит от точности экспериментальных измерений и от того, насколько легко определить вклад различных действий в конечный результат.

Имитация модели может быть построена перед прогоном группы из множества последовательностей через названную имитацию модели. Строят точно согласованную с конкретным процессом имитацию модели, степень простоты которой соответствует требуемой точности и доступному для оптимизации процесса времени.

В некоторых вариантах осуществления указатель приоритетов содержит иерархию условий совпадения в порядке убывания уровня соответствия между действием из последовательности, введенной в имитацию модели, и действиями из последовательностей, входящих в планирование экспериментов, с точки зрения положения действия из введенной последовательности и/или действий, предшествующих действию из введенной последовательности. Это позволяет эффективно использовать доступную информацию о вкладе различных действий, поскольку во всех возможных случаях используют наиболее точные расчеты или измерения вкладов (которые соответствуют оптимальным совпадениям для последовательностей), которые только при необходимости заменяют ближайшими совпадениями.

Для облегчения достижения точного совпадения действий условия совпадения описаны таким образом, чтобы включать: порядок, определяющий число действий, предшествующих действию из последовательности, введенной в имитацию модели, которые должны совпасть с действиями, предшествующими действию из последовательностей планирования экспериментов; и тип определения совпадения положения действия из последовательности, введенной в имитацию модели, в такой последовательности, с положением действия в последовательностях из планирования экспериментов, при этом для совпадения 1-го типа положение действия во введенной последовательности должно совпадать с положением действия в последовательностях из планирования экспериментов, а для совпадения 2-го типа не требуется, чтобы положение действия во введенной последовательности совпадало с положением действия в последовательностях из планирования экспериментов.

Например, для последовательности, состоящей из n-числа действий, указатель приоритетов содержит следующие условия совпадения:

- совпадение n-го порядка 1-го типа,

- совпадение n-го порядка 2-го типа,

- совпадение (n-1)-го порядка 1-го типа,

- совпадение (n-1)-го порядка 2-го типа,

- …

- совпадение 1-го порядка 1-го типа,

- совпадение 1-го порядка 2-го типа,

- совпадение действия в любом положении в последовательности с таким же действием, занимающим первое положение в любой последовательности, используемой в планировании экспериментов.

Таким образом, более высокий приоритет отдают совпадению предшествующих действий, для чего перед тем, как перейти к поиску усеченной подпоследовательности, в моделируемой последовательности осуществляют поиск такой же подпоследовательности действий независимо от их положения. Однако поскольку в некоторых случаях обнаруживается или возникает предположение, что абсолютное положение является более важным, чем влияние предшествующих действий, в качестве альтернативы, для последовательности, состоящей из n-числа действий, указатель приоритетов может содержать следующие условия совпадения:

- совпадение n-го порядка 1-го типа,

- совпадение (n-1)-го порядка 1-го типа,

- совпадение (n-2)-го порядка 1-го типа,

- совпадение 1-го порядка 1-го типа,

- совпадение n-го порядка 2-го типа,

- совпадение (n-1)-го порядка 2-го типа,

- совпадение (n-2)-го порядка 2-го типа,

- …

- совпадение 1-го порядка 2-го типа,

- совпадение действия в любом положении в последовательности с таким же действием, занимающим первое положение в любой последовательности, используемой для планирования экспериментов.

Предпочтительно, планирование экспериментов включает выбор из множества последовательностей тех, которые включают действия, обеспечивающие совпадения по меньшей мере со всеми комбинациями действий, отвечающих условию совпадения выбранного порядка и типа. Это позволяет сосредоточить информацию о рабочих параметрах там, где она имеет наибольшую ценность, с целью обеспечить точный результат при наименьшем количестве информации. Применительно к различным вариантам осуществления данный подход означает, что необходимо осуществлять лишь минимальное число прогонов эталонной модели или минимальное число раз осуществлять процесс, что упрощает и ускоряет оптимизацию. Вместе с тем, дополнительные расчеты с целью определить, какие для этого необходимы последовательности, могут быть сочтены нецелесообразными. В этом случае планирование экспериментов в качестве альтернативы может включать случайный выбор последовательностей из множества последовательностей. В любом случае независимо от типа планирования экспериментов в способе можно дополнительно обуславливать планирование экспериментов. Это позволяет использовать соответствующее планирование экспериментов применительно к каждому процессу, что потенциально обеспечивает более высокую точность, чем использование, например, предыдущего или стандартного планирования, которое в принципе применимо к процессу.

Прогон группы из множества последовательностей через имитацию модели может включать прогон через имитацию модели всех из множества последовательностей. Естественно, это занимает немного больше времени, чем прогон подмножества последовательностей, но обеспечивает наиболее точный результат, несмотря на то, что во многих случаях удовлетворительно точный результат легко достижим при использовании подмножества. При выборе числа последовательностей для прогона через имитацию модели дополнительное время на вычисления компенсируется повышенной точностью.

С учетом вероятных значительных вычислений, которые необходимы, в особенности, в случае сложной эталонной модели, в предпочтительном варианте осуществления способа он по меньшей мере частично реализован при помощи компьютера. Это позволяет эффективно использовать сокращение времени на оптимизацию, которое обеспечивает настоящее изобретение.

После идентификации оптимальной последовательности ее применяют в соответствующем процессе. Таким образом, способ дополнительно заключается в том, что осуществляют последовательный комбинаторный процесс с использованием идентифицированной оптимальной последовательности действий.

В качестве примера применения изобретения последовательный комбинаторный процесс может включать приваривание лопасти к кольцу корпуса заднего подшипника газовой турбины, при этом осуществляемые действия представляют собой отдельные траектории сварки, которые осуществляют последовательно, рабочий параметр, задающий конечный результат, представляет собой деформацию кромки лопасти, а оптимальное значение рабочего параметра представляет собой минимальную величину деформации.

Согласно второй особенности настоящего изобретения предложен компьютерный программный продукт, содержащий машиночитаемые команды для реализации способа оптимизации производственного, промышленного или инженерно-технического последовательного комбинаторного процесса, включающего множество взаимозаменяемых действий, осуществляемых в любой из множества последовательностей с целью достижения конечного результата процесса, характеризуемого рабочим параметром, причем в соответствии с указанными командами компьютер выполняет следующие действия: запоминание планирования экспериментов, включающего группу последовательностей, выбранных из множества последовательностей; запоминание данных, связанных с каждой последовательностью из планирования экспериментов и касающихся значения вклада каждого действия из каждой последовательности из планирования экспериментов в достижение конечного результата, характеризуемого рабочим параметром; прогон группы из множества последовательностей через имитацию модели процесса, в которую в качестве исходных данных вводят последовательность действий и определяют значение конечного результата путем суммирования вкладов в конечный результат каждого действия из каждой введенной последовательности, при этом значения вклада выбирают из значений вклада, которые содержатся в данных о рабочих параметрах, согласно алгоритму, при помощи которого в планировании экспериментов осуществляют поиск соответствия между каждым действием из введенной последовательности и действиями из последовательностей планирования экспериментов согласно указателю приоритетов условий совпадения, извлекают значение вклада совпавшего действия и записывают значения конечного результата каждой последовательности; и идентифицирование оптимальной последовательности путем поиска зарегистрированных оптимальных значений конечного результата в имитации модели с целью обнаружения зарегистрированного оптимального значения рабочего параметра, при этом последовательность, которая обеспечивает такое зарегистрированное оптимальное значение, является оптимальной последовательностью.

Компьютерный программный продукт для реализации изобретения может представлять собой исполняемую на компьютере программу на носителе. Носитель может представлять собой среду для хранения данных, такую как твердотельная, магнитная, оптическая, магнитооптическая или иная запоминающая среда. В качестве альтернативы носитель может представлять собой среду для передачи данных, такую как вещательную, телефонную, сетевую программную, проводную, беспроводную, электрическую, электромагнитную, оптическую или практически любую иную передающую среду.

Согласно третьей особенности настоящего изобретения предложена компьютерная система для реализации способа оптимизации последовательного комбинаторного процесса, включающего множество взаимозаменяемых действий, осуществляемых в любой из множества последовательностей с целью достижения конечного результата процесса, характеризуемого рабочим параметром, содержащая память для запоминания планирования экспериментов, представляющего собой множество последовательностей, выбранных из множества последовательностей, и запоминания данных, связанных с каждой последовательностю из планирования экспериментов и касающихся значения вклада каждого действия из каждой последовательности в достижение конечного результата, характеризуемого рабочим параметром; и процессор, запрограммированный для прогона группы из множества последовательностей через имитацию модели процесса, в которую в качестве исходных данных вводят последовательность действий и определяют значение конечного результата путем суммирования вкладов в конечный результат каждого действия из каждой введенной последовательности, при этом значение вклада выбирают из значений, содержащихся в данных о рабочих параметрах, согласно алгоритму, при помощи которого в планировании экспериментов осуществляют поиск соответствия между каждым действием из введенной последовательности и действиями из последовательностей планирования экспериментов согласно указателю приоритетов условий совпадения, извлекают значения вклада совпавшего действия и осуществляют запись значения конечного результата каждой последовательности в памяти, и идентифицирование оптимальной последовательности путем поиска зарегистрированных оптимальных значений конечного результата в имитации модели с целью обнаружения зарегистрированного оптимального значения рабочего параметра, при этом последовательность, которая обеспечивает такое зарегистрированное оптимальное значение, представляет собой оптимальную последовательность.

Другие особенности, варианты осуществления и примеры настоящего изобретения будут также раскрыты ниже.

Краткое описание чертежей

С целью облегчить понимание изобретения и показать, как оно может быть осуществлено, далее изобретение описано со ссылкой в качестве примера на приложенные чертежи, на которых:

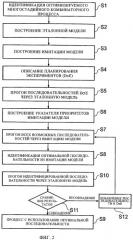
на фиг.1 показана блок-схема последовательности стадий варианта осуществления предлагаемого в изобретении способа,

на фиг.2 - блок-схема последовательности стадий альтернативного варианта осуществления предлагаемого в изобретении способа,

на фиг.3 - вид в перспективе корпуса заднего подшипника газовой турбины, в процессе производства которого применяют один из вариантов осуществления настоящего изобретения,

на фиг.4 - вид в перспективе и вид в поперечном разрезе частей корпуса, показанного на фиг.3,

на фиг.5 - вид в поперечном разрезе лопасти, являющейся частью подшипника, показанного на фиг.3, при этом стрелками указаны траектории, по которым лопасть приваривают к внутреннему кольцу подшипника,

на фиг.6 - таблица с примерами различных последовательностей, в которых осуществляют сварку по траекториям, показанным на фиг.5,

на фиг.7 - диаграммы колебания смещения частей лопасти в процессе сварки,

на фиг.8 - диаграммы колебания смещения части лопасти при сварке в последовательностях, показанных на фиг.6,

на фиг.9 - таблица последовательностей, используемых в планировании экспериментов с целью оптимизации процесса сварки согласно одному из вариантов осуществления настоящего изобретения,

на фиг.10 - матрица событий при различных сочетаниях траекторий сварки согласно последовательностям, показанным на фиг.9,

на фиг.11 - матрица смещения части лопасти в каждом случае, показанном на фиг.10,

на фиг.12 - диаграммы колебания смещения части лопасти при сварке в некоторых из последовательностей, показанных на фиг.9, и

на фиг.13 - диаграмма колебания окончательного смещения части лопасти при сварке в каждой последовательности, показанной на фиг.9.

Подробное описание

В настоящем изобретении предложен метод применения к последовательным комбинаторным задачам подхода, основанного на имитации модели, который ранее использовался для нахождения оптимальных решений непрерывных численных задач. Имитация модели значительно сокращает расходы на вычисления, необходимые для оптимизации таких процессов, по сравнению с обычными подходами, основанными на сложных методах компьютерного моделирования, таких как анализ методом конечных элементов.

Последовательный комбинаторный процесс представляет собой процесс, состоящий из множества стадий или действий, которые являются взаимозаменяемыми в том смысле, что могут быть осуществлены в любой из нескольких или множества последовательностей, при этом одни действия, возможно, заменяют другие действия или существует возможность выбора способов осуществления каждого действия с целью получения такого же общего конечного результата, но качество такого конечного результата зависит от конкретного порядка следования действий.

Таким образом, в каждом положении последовательности осуществляют какое-либо действие, выбранное из группы действий, число которых равно числу положений в последовательности, или из более многочисленной группы действий. В последнем случае в более многочисленную группу входят некоторые действия, которые могут быть исключены из процесса или заменены другими действиями или, в качестве альтернативы, некоторыми или всеми действиями, соответствующие параметры которых могут иметь различные значения (например, осуществление конкретной стадии при одной из нескольких различных температур или в течение одного из нескольких отрезков времени), в результате чего каждое действие имеет несколько возможных вариантов, каждый из которых может сам по себе рассматриваться как действие, несмотря на то, что в любую взятую последовательность будет включен лишь один из вариантов.

Конечный результат рассматривают как описанный рабочим параметром. Природа рабочего параметра зависит от конкретного процесса, и он может, например, представлять собой размеры производимой детали или время, которое занимает осуществление процесса. Так, для каждой возможной последовательности процесса предусмотрен конечный результат, который имеет значение, описанное рабочим параметром.

В приведенном выше примере с размером конечными результатами будут являться различные значения размеров.

Что касается примера со временем, конечными результатами будут являться различные количества времени.

Поскольку каждое действие из заданной последовательности определенным образом способствует конечному результату в зависимости как от его положения в последовательности, так и природы самого действия, корректировка выбранных действий приводит к изменению значения конечного результата.

В ряду последовательностей существует последовательность, конечный результат которой имеет такое значение, которое обеспечивает оптимальное значение рабочего параметра, такое как кратчайшее время или наименьшие размеры. Поскольку не всегда очевидно, какая последовательность обеспечивает такой оптимальный результат, желательно иметь возможность определить такую последовательность, что может рассматриваться как оптимизация комбинаторного процесса. Да настоящего времени это было достижимо, как правило, при помощи сложного моделирования. Обычно моделирование одной последовательности занимает много часов, как это происходит при моделировании методом конечных элементов. Даже для процесса с относительно небольшим числом действий общее количество комбинаций действий может быть огромным, поэтому проверка каждой комбинации путем моделирования становится неосуществимой. В настоящем изобретении предложено применение более простой имитации модели, чтобы частично сократить затраты вычислительных ресурсов и, следовательно, ускорить процесс.

Таким образом, в настоящем изобретении предложен метод комбинаторной оптимизации. Оптимизация представляет собой процесс обнаружения одного или нескольких лучших или оптимальных решений в четко заданной дискретной области решения задачи. Область является дискретной, поскольку существует лишь ограниченное число действий и каждое действие входит или не входит в заданную последовательность; так, последовательная комбинаторная задача имеет отношение к эффективному распределению ограниченных ресурсов с целью достижения заданных целей, когда значения некоторых или всех переменных величин ограничены целыми числами. Ограничения на основные ресурсы, такие как время, рабочая сила, поставки или капитал, способны сузить возможные альтернативы, считающиеся осуществимыми. Такие проблемы возникают почт