Способ анализа сигналов о состоянии объекта

Способ анализа сигналов о состоянии объекта

Иллюстрации

Показать все

Реферат

Изобретение относится к технической кибернетике и может быть использовано для определения состояний объектов при их диагностировании.

Известен способ анализа сигнала о состоянии объекта (Киселев Н.В., Сечкин В.А. Техническая диагностика методами нелинейного преобразования. - Л.: Энергия, 1980, 109 с.), включающий формирование с последующей коррекцией распознающих эталонов на основе обучающих сигналов, сравнение распознающих эталонов с анализируемым сигналом с получением набора оценок о принадлежности реального состояния объекта каждому из множества возможных состояний объекта, сравнение полученных оценок между собой и с заданным порогом распознавания, в результате которого формируется решение о предполагаемом состоянии объекта. Недостатком данного способа является невозможность оценить достоверность процесса обучения и распознавания, что является критическим в условиях шумов, приводящих к слабой различимости сигналов, относящихся к разным состояниям объекта.

Выявленный недостаток устраняет способ анализа сигналов о состоянии объекта (Патент РФ № 2090928. кл. G06K 9/00, G06K 9/62, G06K 9/66. Способ анализа сигналов о состоянии объекта), позволяющий распознавать состояние объекта путем введения механизма измерения достоверности сигналов и эталонов через сравнение сигналов с эталонами по нормированной шкале. Данный способ выбран в качестве прототипа.

Недостатком этого способа является ограниченность его применения, выражающаяся в возможности анализировать только оцифрованные сигналы о состоянии объекта и невозможности анализировать сигналы о состоянии объекта, представленные не только в оцифрованном виде, но и (или) в виде двухградационного изображения на неквантованной плоскости. Применение способа-прототипа предполагает, что количество классов состояний объекта известно заранее, что ограничивает сферу его применения в случаях, когда это количество неизвестно. Отсутствие механизма предварительного объективного разделения сигналов по классам состояний, учитывающего изменение формы сигналов во времени, в свою очередь, допускает возможность определения ложного класса или необъективного объединения множества сигналов в ложные классы состояний объекта, что снижает достоверность дальнейшего определения состояния объекта.

Техническим результатом реализации предлагаемого способа являются расширение функциональных возможностей в применении способа анализа сигналов, представленных как в цифровом виде, так и (или) в виде двухградационного изображения на неквантованной плоскости, с неизвестным заранее количеством классов состояний объекта, а также повышение достоверности распознавания состояния объекта в системах технической кибернетики.

Этот результат достигается тем, что в способ-прототип, включающий нормировку, формирование и коррекцию распознающих эталонов, оптимизацию и сравнение сигналов и эталонов в евклидовом векторном пространстве с последующим распознаванием состояния объекта до тех пор, пока результат распознавания не удовлетворит заданному критерию достоверности или неудачи, введено до этапа нормировки цепное кодирование сигналов, представленных как в цифровом виде, так и (или) в виде двухградационного изображения на неквантованной плоскости и описывающих состояние объекта, а также определение минимального количества классов для этих состояний по всем цепям.

Заявленный способ поясняется чертежами, на которых показаны:

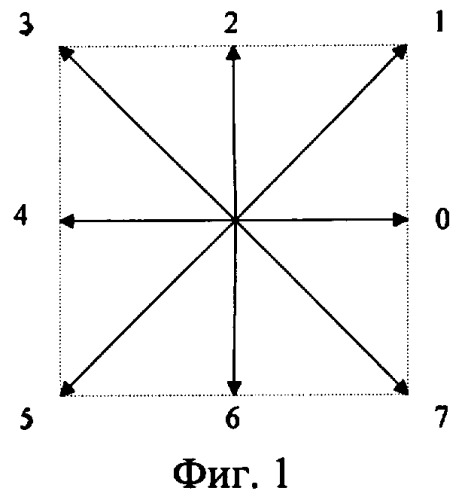
фиг.1 - коды описания направления произвольной кривой;

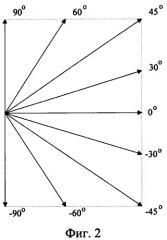
фиг.2 - коды описания однонаправленной кривой;

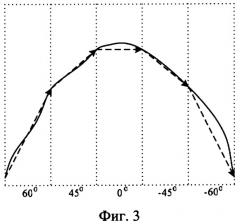
фиг.3 - пример кодирования участка однонаправленной кривой;

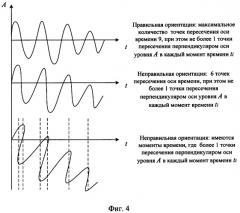
фиг.4 - пример ориентации сигнала в виде двухградационного изображения на неквантованной плоскости по оси времени;

фиг.5 - анализируемые сигналы в виде двухградационного изображения на неквантованной плоскости;

фиг.6 - сигналы на квантованной по времени плоскости;

фиг.7 - сигналы в форме цепей на квантованной по времени плоскости;

фиг.8 - таблица цепей в виде одномерных массивов данных;

фиг.9 - таблица преобразованных по синусу цепей;

фиг.10 - таблица евклидовых расстояний между парами цепей;

фиг.11 - таблица евклидовых расстояний между парами цепей после первого объединения в общий класс;

фиг.12 - таблица евклидовых расстояний между парами цепей после второго объединения в общий класс;

фиг.13 - таблица евклидовых расстояний между парами цепей после третьего объединения в общий класс;

фиг.14 - дерево иерархической классификации цепей со значениями порогов объединения в классы;

фиг.15 - таблица евклидовых расстояний между средней цепью ортогонального пространства и классификационными цепями;

фиг.16 - таблица оценок состояний объекта на основе тестовых электроэнцефалограмм (ЭЭГ) для класса А с оптимизацией;

фиг.17 - таблица оценок состояний объекта на основе тестовых ЭЭГ для класса В с оптимизацией.

Множество параметров, характеризующих состояние той или иной системы, изменяющихся во времени представляет собой некую кривую. Для различного класса состояний той или иной системы формы кривых для их описания должны быть различными. В технических системах наиболее распространен периодический характер кривых. Известен метод представления произвольной кривой под названием цепного кодирования [3]. Данный метод позволяет представить в цифровой форме любую кривую, заданную в виде двухградационного изображения на неквантованной плоскости. В результате применения цепного кодирования сигнал произвольной формы представляется в виде кода, описывающего направление сигнала в равные временные интервалы кодами, показанными на фигуре 1.

Так как сигналы, характеризующие состояние системы, изменяются во времени и не имеют обратного хода, то нет необходимости использовать коды обратного направления. Однако увеличение градаций для кодов положительного направления кривой позволит более детально описывать изменяющуюся во времени форму однонаправленной кривой. Таким образом, от фигуры 1 можно перейти к фигуре 2. В соответствии с кодировкой однонаправленная кривая преобразовывается к последовательности, состоящей из n кодов. Данную последовательность называют цепью [3]. Графическая интерпретация данного преобразования для участка однонаправленной кривой представлена на фигуре 3.

Если имеются две кривые одинаковой ориентации и равной длительности по времени, при этом необходимо измерить сходство между ними, данные кривые преобразовываются с помощью кодов описания однонаправленной кривой в цепи а=а₁,…,а_n и b=b₁,…,b_n. Мерой сходства цепей при заданном пороге классификации является d_ab - евклидово расстояние между парой цепей а и b, вычисляемое по формуле [4]:

где n - количество элементов цепи;

i - текущее значение элемента цепи.

Предлагаемый способ является дополнением к способу-прототипу. Он осуществляется до этапа нормировки и состоит из цепного кодирования анализируемых сигналов, представленных как в цифровом виде, так и (или) в виде двухградационного изображения на неквантованной плоскости, а также определения минимального пространства классов для множества сигналов, характеризующих состояние системы.

Реализация цепного кодирования сигналов, представленных в виде двухградационных изображений на неквантованной плоскости, предполагает выполнение следующих действий:

1. Ориентация каждого анализируемого сигнала, представленного кривой в виде двухградационного изображения на неквантованной плоскости, по осям времени и уровня сигнала, таким образом, чтобы достигалось максимальное количество пересечений кривой с осью времени и не более одного пересечения с осью уровня сигнала, являющейся перпендикуляром оси времени в каждый единичный момент времени.

2. Определение из всего множества анализируемых сигналов сигнала с максимальным количеством пересечений временной оси.

3. Определение показателя дискретизации квантованной по времени плоскости.

4. Построение квантованной плоскости.

5. Кодировка каждой однонаправленной кривой по квантованной плоскости в цепь.

Цепное кодирование анализируемых сигналов, представленных в виде массива оцифрованных отсчетов, предполагает выполнение следующих действий:

1. Нормировка оцифрованных отсчетов для каждого анализируемого сигнала в одномерный массив с математическим ожиданием, равным 0, и дисперсией, равной 1.

2. Разбиение каждого одномерного массива оцифрованных отсчетов на участки, определяемые показателем дискретизации квантованной по времени плоскости.

3. Выделение начальных и конечных отсчетов для каждого участка массива.

4. Определение арксинуса разности между значениями начального и конечного отсчетов для каждого участка массива.

Определение минимального пространства классов для множества сигналов, характеризующих состояние системы, предполагает выполнение следующих действий:

1. Иерархическая классификация цепей с определением порогов объединения в классы.

2. Расчет евклидова расстояния между классами цепей и средней цепью ортогонального пространства, совпадающей с временной осью.

3. Объединение классов цепей со значением порога объединения в общий класс, не превышающим минимального значения евклидова расстояния между классами цепей и средней цепью ортогонального пространства.

Реализация предлагаемого способа анализа сигналов о состоянии объекта осуществляется следующим образом.

Ориентация каждого анализируемого сигнала, представленного кривой в виде двухградационного изображения на неквантованной плоскости, по осям времени и уровня сигнала, осуществляется таким образом, чтобы достигалось максимальное количество пересечений сигналом оси времени и не более одного пересечения с осью уровня сигнала, являющейся перпендикулярной прямой оси времени в каждый единичный момент времени. На фигуре 4 графически представлены примеры реализации предлагаемого правила ориентации по временной оси сигнала, представленного в виде двухградационного изображения на неквантованной плоскости.

Цепное кодирование ориентированных по оси времени сигналов, представленных в виде двухградационных изображений на неквантованной плоскости, осуществим на примере сигналов, предложенных в способе-прототипе пятью классами сигналов. Графически пять классов сигналов, ориентированных по оси времени в виде двухградационных изображений на неквантованной плоскости, представлены на фигуре 5.

Выявление сигнала с максимальным количеством пересечений стандартизованного нулевого уровня всей группы сигналов осуществляется тем, что для каждого сигнала подсчитывают количество пересечений оси времени k_i и определяют максимальное значение k_max среди всех сигналов. Так как любой период сигнала имеет по крайней мере два значения пересечения нулевого уровня для этого периода, то показатель дискретизации квантованной плоскости относительно общей для всех сигналов оси времени определяется как

Фактически значение n определяет количество элементов цепи.

Формирование квантованной плоскости представляет собой разбиение неквантованной области каждого сигнала длительностью по времени t_c, начиная с нулевого значения времени t₀, на n равных по длительности временных интервалов. В результате данной процедуры имеем множество квантованных по времени сигналов. На фигуре 6 графически представлены классы сигналов на квантованной по времени плоскости. На каждом n-ом участке для каждого сигнала определяется угол между точками, пресекающими соседние квантованные временные оси. В результате чего получается количество цепей, равное общему количеству анализируемых сигналов. В рассматриваемом примере число элементов цепи для каждого сигнала равно 32. На фигуре 7 изображены сигналы в форме цепей на квантованной по времени плоскости.

Кодировка каждой однонаправленной кривой по квантованной плоскости в цепь заключается в представлении каждой анализируемой кривой в виде одномерного массива данных, где элементами этого массива являются значения углов для каждого n квантованного участка. На фигуре 8 представлена таблица, где цепи для каждого класса определены массивом значений углов для каждого n участка, при этом интервал измерения углов был определен как

При представлении анализируемых сигналов в виде одномерных массивов оцифрованных отсчетов, совпадающих по длительности во времени с сигналами в виде двухградационных изображений на неквантованной плоскости, цепное кодирование осуществляется следующим образом. Так как при оцифровке анализируемых сигналов могут использоваться аналогово-цифровые преобразователи различной разрядности, то для предотвращения превосходства признаков с большими числовыми значениями при вычислении расстояний осуществляется нормировка цифровых последовательностей. Все анализируемые цифровые сигналы преобразуются в одномерные массивы с математическим ожиданием, равным 0, и значением дисперсии, равной 1. Данное преобразование для каждого i-го значения отсчета одномерного массива k-го анализируемого сигнала к значению осуществляется в соответствии с выражением [3]:

где µ_k - математическое ожидание одномерного массива отсчетов k-го анализируемого сигнала;

σ_k - стандартное отклонение одномерного массива отсчетов k-го анализируемого сигнала.

Данное преобразование позволит нормировать цифровые сигналы с различными значениями квантования по уровню к цифровым последовательностям единой размерности. Далее каждую k-ю преобразованную цифровую последовательность разбивают на n участков, определяемых показателем дискретизации по временной плоскости. Для каждого m из n участков k-й преобразованной цифровой последовательности определяют начальные значения и формируют новую цифровую последовательность объемом n. Таким образом получают k цифровых последовательностей, включающих в себя по n элементов. Преобразование k-й преобразованной цифровой последовательности в цепь x_k осуществляется вычислением арксинуса разности между n соседними нормированными отсчетами и при и i∈[1;n] в соответствии с выражением

В результате данного преобразования формируется цепь x_k, элементами которой являются значения углов для n участков с интервалом измерения углов

Определение минимального пространства классов для множества цепей предполагает проведение следующих действий. Осуществляется процедура иерархической классификации в метрике евклидового расстояния по правилу связывания «ближайшего соседа» [3], что позволяет построить дерево иерархической классификации [4] и определить пороги объединения анализируемых сигналов в объединенные классы. Далее, осуществляется расчет евклидова расстояния между классами цепей и средней цепью ортогонального пространства, совпадающей с временной осью. Сравниваются пороги объединения цепей в классы с минимальным евклидовым расстоянием между классами и средней цепью ортогонального пространства. Классы цепей с порогом объединения в один класс по дереву иерархической классификации, меньшим минимального евклидова расстояния между классами и средней цепью ортогонального пространства, объединяются в один класс.

Поясним выполнение описанных действий на примере.

Для сокращения размерности значений евклидова расстояния между полученными в результате цепного кодирования цепями возьмем синус каждого значения угла, представленного на фигуре 8. В результате данного преобразования таблица фигуры 8 примет вид таблицы, представленной на фигуре 9. По формуле (1) рассчитаем евклидовы расстояния между парами одномерных массивов данных, принадлежащих каждому классу. Результат вычислений отобразим на фигуре 10 в виде таблицы евклидовых расстояний между классами А, В, С, D, Е.

Минимальное значение в таблице на фигуре 10, равное 1,96, соответствует расстояниям между классами А и В, т.е. d_A,B=d_B,A=1,96, что означает их наибольшую близость среди всех других возможных пар. После объединения данных объектов в один класс получим четыре класса: АВ, С, D, Е.

Пересчитаем матрицу расстояний для нового множества объектов классификации, применяя правило «ближайшего соседа» для расчета расстояния между классом АВ и остальными классами. Так, расстояние между классами С и АВ будет равно

d_C,(A,B)=min(d_C,A;d_C,B)=min(2,61;2,18)=2,18.

Матрица расстояний для первого шага объединения представлена таблицей на фигуре 11.

Минимальное значение в таблице на фигуре 11, равное 2,18, соответствует расстояниям между классами С и АВ, т.е. d_AB,C=d_C,AB=2,18, что означает их наибольшую близость среди всех других возможных пар. После объединения данных объектов в один класс получим три класса: ABC, D, Е с порогом объединения в метрике евклидова расстояния 2,18.

Матрица расстояний для второго шага объединения представлена таблицей на фигуре 12.

Минимальное значение в таблице на фигуре 12, равное 3,30, соответствует расстояниям между классами ABC и Е, т.е. d_ABC,E=d_E,ABC=3,30, что означает их наибольшую близость среди всех других возможных пар. После объединения данных объектов в один класс получим два класса: АВСЕ, D с порогом объединения в метрике евклидова расстояния 3,30.

Матрица расстояний для третьего шага объединения представлена таблицей на фигуре 13. Из таблицы видно, что порог объединения всех классов в один класс в метрике евклидова пространства равен 4,25.

Дерево иерархической классификации для рассматриваемых цепей представлено на фигуре 14. Дерево иерархической классификации или дендограмма графически изображает иерархическую структуру, порожденную матрицей сходства и правилом объединения в классы [4].

В пределах плоскости, ограниченной временным интервалом наблюдения, можно представить бесконечное множество пар ортогональных сигналов, которые в евклидовой метрике обеспечивают максимальные значения и образуют между собой не подлежащие парному объединению классы. Средним сигналом для каждой пары ортогональных сигналов в этой плоскости выступает нулевой по уровню сигнал, совпадающий с временной осью. Таким образом, средняя цепь ортогонального пространства представляет собой одномерный массив, состоящий из n нулевых значений. Обозначим среднюю цепь ортогонального пространства классом О.

По формуле (1) рассчитаем евклидовы расстояния между средней цепью ортогонального пространства и остальными классификационными цепями. Результат расчета представлен на фигуре 15 в виде таблицы евклидовых расстояний между средней цепью - классом О и классами А, В, С, D, Е. Минимальное значение евклидова расстояния в данной таблице равно 2,08, что в свою очередь превышает значение порога объединения классов А и B в один класс АВ, следовательно, классы А и В необходимо объединить в один совместный класс АВ. Пороги объединения остальных классов превышают порог, равный 2,08, следовательно, объединение остальных классов производить не следует.

Таким образом, введение в способ-прототип предварительного цепного кодирования сигналов, описывающих состояние объекта, а также определения минимального количества классов для этих состояний по всем цепям, позволило устранить субъективность предварительного разбиения пространства классификации на отдельные классы.

Получение четырех классов анализируемых сигналов о состоянии объекта вместо пяти, как в способе-прототипе, позволяет избежать неудовлетворительных оценок состояний объекта на основе тестовых фрагментов электроэнцефалограмм (ЭЭГ) для класса А и класса В. Неудовлетворительные оценки состояний объекта на основе тестовых фрагментов ЭЭГ в способе-прототипе с оптимизацией для класса А и класса В отображены на фигурах 16, 17 соответственно и выделены полужирным шрифтом. В результате объективного объединения классов А и B в единый класс негативные оценки исчезнут, что повысит достоверность распознавания состояния объекта.

Проведенный анализ существующих способов позволил установить, что аналоги, тождественные признакам заявленного технического решения, отсутствуют, что указывает на соответствие заявленного способа условию патентоспособности «новизна». Введенные отличительные признаки: применение механизма объективного разделения сигналов, описывающих состояние объекта по классам состояний, учитывающим изменение формы сигналов во времени на основе цепного кодирования, в аналогах не встречаются. Следовательно, заявляемый способ соответствует критерию «изобретательский уровень».

Промышленная применимость способа заключается в возможности его использования для диагностирования объектов в отрасли технической кибернетики и реализации этапов способа на существующей в настоящее время элементной базе.

Источники информации

1. Киселев Н.В., Сечкин В.А. Техническая диагностика методами нелинейного преобразования. - Л.: Энергия, 1980, 109 с.

2. Патент РФ № 2090928. кл. G06K 9/00, G06K 9/62, G06K 9/66, 1997. Способ анализа сигналов о состоянии объекта.

3. Теория распознавания и анализ сцен: Пер. с англ./ P.O.Дуда, П.Е.Харт.; под. ред. Стефанюка В.Л. - М.: Мир, 1976. - 511 с.

4. Факторный, дискриминантный и кластерный анализ: Пер. с англ./ Дж. - О.Ким, Ч.У.Мьюллер, У.Р.Клекка и др.; под. ред. Енюкова И.С. - М.: Финансы и статистика, 1989. - 215 с.: ил.

1. Способ анализа сигналов о состоянии объекта, включающий в себя нормирование всех сигналов о состоянии объекта, формирование на этапе обучения распознающих эталонов первого уровня, формирование оптимизирующего эталона первого уровня, на основе которого из распознающих эталонов первого уровня формируют оптимизированные распознающие эталоны второго уровня, а на этапе распознавания формируют оптимизированный сигнал о состоянии объекта аналогично оптимизации распознающих эталонов, сравнивают оптимизированный сигнал с каждым из оптимизированных распознающих эталонов соответствующего уровня, формируют величины оценок состояния объекта, сравнивают их с заданным порогом распознавания, выделяют подмножество величин оценок, превышающих порог распознавания, выделяют соответствующее выделенному подмножеству величин оценок подмножество распознающих эталонов, на основе которого повторяют процесс оптимизации распознающих эталонов и анализируемого сигнала с последующим распознаванием состояния объекта до тех пор, пока результат распознавания не удовлетворит заданному критерию достоверности или неудачи, отличающийся тем, что предварительно до этапа обучения осуществляют цепное кодирование сигналов о состоянии объекта, определяют минимальное количество классов состояний для распознающих эталонов.

2. Способ по п.1, отличающийся тем, что цепное кодирование сигналов о состоянии объекта осуществляется ориентацией каждого анализируемого сигнала, представленного в виде двухградационного изображения на неквантованной плоскости, по осям времени и уровню сигнала, из всего множества анализируемых сигналов выявляется сигнал с максимальным количеством пересечений временной оси, определяется показатель дискретизации квантованной по времени плоскости, осуществляется построение квантованной плоскости, далее каждая однонаправленная кривая кодируется с использованием квантованной по времени плоскости в цепь.

3. Способ по п.2, отличающийся тем, что цепное кодирование сигналов о состоянии объекта осуществляется как для сигналов, представленных в цифровом виде, так и в виде двухградационного изображения на неквантованной плоскости.

4. Способ по п.1, отличающийся тем, что определение минимального количества классов состояний осуществляется применением иерархической классификацией цепей с определением порогов объединения в классы, определением евклидовых расстояний между классами цепей и средней цепью ортогонального пространства, объединением различных классов цепей в один класс при значении порога объединения, не превышающем значения минимального евклидова расстояния между классами цепей и средней цепи ортогонального пространства.