Вычислительное устройство

Вычислительное устройство

Иллюстрации

Показать все

Реферат

Изобретение относится к вычислительной технике и может быть использовано в цифровых вычислительных устройствах, а также в устройствах для формирования элементов конечных полей и в криптографических приложениях.

Известно устройство для формирования остатка по произвольному модулю от числа, содержащее регистр, блок ключей, блок сумматоров и элемент задержки, соединенные между собой функционально (см. АС СССР №1633495, кл. Н03М 7/18, 1989).

Недостатком данного устройства является низкая надежность его функционирования и небольшая область функциональных возможностей.

Наиболее близким по технической сущности к заявляемому изобретению является рекуррентный формирователь остатков по произвольному модулю, содержащий блок сумматоров, блок формирования частичных остатков, инвертор, элемент задержки и регистр, соединенные между собой функционально (см. патент РФ №2007037, кл. Н03М 7/18, 30.01.1994, бюл. №2).

Недостатком данного устройства являются его ограниченные функциональные возможности, а именно отсутствие возможности формирования неполного частного.

Цель изобретения - расширение функциональных возможностей устройства за счет обеспечения формирования неполного частного.

Для достижения поставленной цели в вычислительное устройство, содержащее элемент задержки и регистр, причем вход начала вычисления устройства соединен со входом записи регистра и со входом элемента задержки, выход которого является выходом окончания процесса вычисления, вход числа устройства соединен с информационными входами регистра, введены (n-k+1) сумматоров и (n-k+1) мультиплексоров, причем на входы переноса всех сумматоров подается логическая единица, выход переноса i-го сумматора соединен с управляющим входом i-го мультиплексора и является выходом (n-k-i+1)-го разряда неполного частного устройства, где i=1,…,(n-k+1) номер ступени преобразования, на первый информационный вход i-го сумматора подается инверсный код модуля, сдвинутый на (n-k-i+1) разрядов в сторону старших, причем выход (i-1)-го, где i=2,…,(n-k+1), мультиплексора соединен с первым входом i-го мультиплексора и со вторым информационным входом i-го сумматора, выход (i-1)-го сумматора соединен со вторым информационным входом (i-1)-го мультиплексора, причем выход регистра соединен с первым информационным входом первого мультиплексора и со вторым информационным входом первого сумматора, выход (n-k+1)-го сумматора является выходом вычислительного устройства.

Сущность изобретения заключается в реализации следующего способа формирования остатка по произвольному модулю.

Пусть требуется сформировать остаток r от числа а по модулю р и вычислить частное q, то есть решить уравнение a=qp+r.

При проведении вычислений по модулю р значение числа а сравнивается со значением числа z=p×2^n-k, где n количество разрядов числа а, a k количество разрядов модуля р. Если значение a≥z, то из числа а вычитается значение числа z, то есть a₁=a-z, при этом формируется ненулевой старший (n-k+1)-й разряд неполного частного q. Если a<z, то число а остается без изменений а₁=а, а значение старшего (n-k+1)-го разряда неполного частного q принимается равным нулю. Полученное в результате значение а₁ сравнивается со значением z₁=p×2^n-k-1. Если значение a₁≥z₁, то из а₁ вычитается значение модуля z₁, то есть а₂=а₁-z₁, при этом формируется ненулевой (n-k)-й разряд неполного частного q. Если a₁<z₁, то число а₁ остается без изменений а₂=а₁, а значение (n-k)-го разряда неполного частного q принимается равным нулю. Полученное в результате значение а₂ сравнивается со значением z₂=p×2^n-k-2 и т.д. На последнем (n-k+1)-м шаге число a_n-k сравнивается с модулем p. Если значение a_n-k≥p, то из a_n-k вычитается значение числа р, то есть a_n-k+1=a_n-k - Р, при этом формируется ненулевой младший разряд неполного частного q. Если а_n-k<р, то число а_n-k остается без изменений a_n-k+1=a_n-k, а значение младшего разряда неполного частного q принимается равным нулю. Полученное в результате значение r=a_n-k+1 является остатком от деления числа а на число р.

Предлагаемое вычислительное устройство осуществляет данный метод путем последовательного выполнения (n-k+1) операций, в ходе i-й операции значение а_i сравнивается со значением р×2^n-k-i путем вычисления разности a_i-p×2^n-k-i, где i=1,…,(n-k), и формируется (n-k-i)-й разряд неполного частного q. При выполнении (n-k+1)-й операции результатом вычисления числа а по модулю р будет являться значение разности, полученное на последнем (n-k+1)-м шаге.

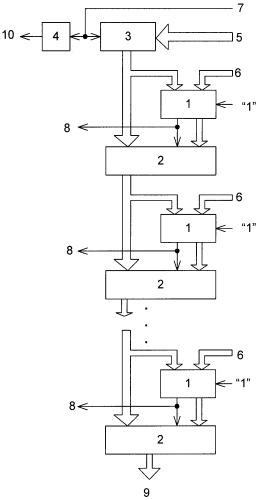
На чертеже представлена схема вычислительного устройства.

Вычислительное устройство содержит (n-k+1) сумматоров 1, (n-k+1) мультиплексоров 2, регистр 3 и элемент 4 задержки. Вход 5 служит для подачи двоичного кода числа а, вход 6 - для подачи двоичного кода модуля р. Вход 7 начала вычисления соединен со входом записи регистра 3 и входом элемента 4 задержки. На вход 6 подается двоичный инверсный код числа р×2^n-k-i, где i=1, …, (n-k) порядковый номер ступени преобразования, a (n-k) количество ступеней преобразования, n равно количеству разрядов двоичного представления числа a, k равно количеству разрядов двоичного представления модуля p. Инверсный код числа p×2^n-k-i может быть получен путем сдвига двоичного кода числа р на i разрядов в сторону старшего с последующей его инверсией. Выход 9 является выходом двоичного кода остатка r, а выход 8 является выходом двоичного кода неполного частного q. Выход 10 элемента 4 задержки - выходом окончания процесса вычисления.

Вычислительное устройство работает следующим образом.

На вход 3 подается двоичный код числа а, который далее поступает на информационные входы регистра 3. Одновременно на вход 7 начала вычисления подается импульс, который поступает на вход элемента 4 задержки и на вход записи регистра 3. При этом код числа а записывается в регистр 3, появляется на его информационных выходах и поступает на второй вход сумматора 1 и первый вход мультиплексора 2 первой ступени преобразования. На первый вход сумматора 1 подается инверсный код p×2^n-1 со входа 4 устройства. На вход переноса всех сумматоров 1 подается логическая единица. Сумматор 1 выполняет операцию, описываемую выражением: , где с - результат суммирования, а - входное число, р - модуль, n - количество разрядов числа а. Старший n+1 разряд полученного значения с поступает на выход переноса сумматора 1. Остальные разряды представляют собой разность . На первый вход мультиплексора 2 поступает код числа а, на второй вход мультиплексора 2 поступает разность . Если сигнал на выходе переноса сумматора 1 равен "1", то на второй вход сумматора 1 второй ступени преобразования и на первый вход мультиплексора 2 второй ступени преобразования поступает разность , если же он равен "0", то на второй вход сумматора 1 и на первый вход мультиплексора 2 поступает само число а. На первый вход сумматора 1 второй ступени преобразования поступает инверсный код р×2^n-2. Далее выполняются те же действия, что и на первой ступени преобразования. После проведения n таких операций на выходе 4 окажется результат вычисления числа а по модулю р, а на выходах 6 - код неполного частного q. Одновременно с выхода элемента 4, время задержки которого равно времени работы (n-k+1) сумматоров 1 и (n-k+1) мультиплексоров 2, на выход 10 поступает импульс, сигнализирующий об окончании процесса формирования остатка и неполного частного.

Рассмотрим работу вычислительного устройства на примере.

Пусть a=189₁₀=10111101₂, модуль р=19₁₀=10011₂, , n=8, k=5. Первый сумматор формирует значение . Старший разряд c₁ равен 1, следовательно, мультиплексор 2 переводит на второй сумматор код числа а₁=а-p×2^n-k=00100101₂ и 3-й разряд неполного частного q принимает значение 1. Второй сумматор 1 формирует значение . Старший разряд с₂ равен 0, следовательно, мультиплексор 2 переводит на третий сумматор 1 код числа а₁ и 2-й разряд неполного частного q принимает значение 0. Третий сумматор 1 формирует значение . Старший разряд с₃ равен 0, следовательно, мультиплексор 2 переводит на четвертый сумматор 1 код числа а₁ и 1-й разряд неполного частного q принимает значение 0. Четвертый сумматор 1 формирует значение . Старший разряд с₄ равен 1, следовательно, мультиплексор 2 переводит на выход код числа

a₂=a₁-p×2^n-k-3=10010₂=18₁₀ и 0-й разряд неполного частного q принимает значение 1. В результате неполное частное имеет значение q=1001₂=9₁₀

189=19×9+18

Вычислительное устройство, содержащее элемент задержки и регистр, причем вход начала вычисления устройства соединен со входом записи регистра и со входом элемента задержки, выход которого является выходом окончания процесса вычисления, вход числа устройства соединен с информационными входами регистра, отличающееся тем, что в него введены (n-k+1) сумматоров и (n-k+1) мультиплексоров, где n - количество разрядов двоичного представления числа a, k - количество разрядов модуля р, причем на входы переноса всех сумматоров подается логическая единица, выход переноса i-го сумматора соединен с управляющим входом i-го мультиплексора и является выходом (n-k-i+1)-го разряда неполного частного устройства, где i=1,…,(n-k+1) номер ступени преобразования, на первый информационный вход i-го сумматора подается инверсный код модуля, сдвинутый на (n-k-i+1) разрядов в сторону старших, причем выход (i-1)-го, где i=2,…,(n-k+1), мультиплексора соединен с первым входом i-го мультиплексора и со вторым информационным входом i-го сумматора, выход (i-1)-го сумматора соединен со вторым информационным входом (i-1)-го мультиплексора, причем выход регистра соединен с первым информационным входом первого мультиплексора и со вторым информационным входом первого сумматора, выход (n-k+1)-ого сумматора является выходом вычислительного устройства.