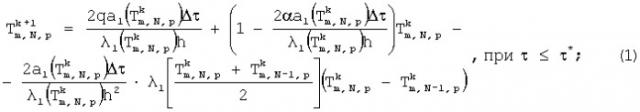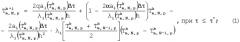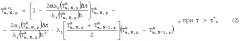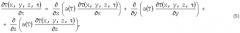Способ идентификации комплекса теплофизических свойств твердых материалов для обнаружения скрытых объектов (мин) в грунте

Способ идентификации комплекса теплофизических свойств твердых материалов для обнаружения скрытых объектов (мин) в грунте

Иллюстрации

Показать все

Реферат

Предлагаемое изобретение относится к обнаружению подповерхностных объектов (мин) методами оптической локации с применением авиационно-космической съемки земной поверхности в инфракрасном диапазоне. Изобретение может быть использовано для обнаружения и идентификации объектов (мин), расположенных в глубине грунта, как при пассивном зондировании, так и при активном - путем нагрева поверхности почвы инфракрасным излучателем.

Известен способ идентификации комплекса теплофизических свойств твердых материалов [патент РФ 2303777], включающий тепловое импульсное воздействии от линейного источника нагрева на плоскую поверхность исследуемого и эталонного образцов, измерение избыточной температуры на плоской поверхности образцов на фиксированном расстоянии от линии нагрева с момента подачи теплового импульса, импульсное воздействие и измерение избыточной температуры осуществляют в плоскости контакта исследуемого и эталонного образцов, а измерение избыточной температуры производят в одной точке в заданном интервале времени, используя математическую модель прямой задачи теплопроводности на основе метода конечных разностей.

Недостатком этого способа является необходимость производить контакт исследуемого материала и эталонного, что не позволяет реализовать задачу обнаружения скрытых объектов (мин) в грунте. Кроме того, в способе-прототипе производится идентификация теплофизических свойств материала только на его поверхности, а используемая двумерная численная модель не в полной мере описывает реальные тепловые процессы.

Техническим результатом предлагаемого изобретения является применение способа идентификации теплофизических свойств твердых материалов по новому назначению, в частности, для обнаружения скрытых объектов (мин) в грунте с использованием инфракрасной термографической авиационно-космической съемки.

Сущность изобретения заключается в том, что в способе идентификации комплекса теплофизических свойств твердых материалов для обнаружения скрытых объектов в грунте осуществляют тепловое импульсное воздействие от инфракрасного источника нагрева на плоскую поверхность грунта, измерение избыточной температуры на плоской поверхности грунта в заданном интервале времени, расчет математической модели прямой задачи теплопроводности на основе метода конечных разностей, измерение избыточной температуры производят во всех точках зондируемой поверхности грунта, применяют трехмерную промежуточную сеточную функцию источника нагрева:

при , ,

трехмерную сеточную функцию на k+1 временном слое:

при i=1, , , .

рассчитывают численную модель скрытого объекта с теплофизическими свойствами {а₂, λ₂}, расположенного между точками [М-1, µ, Р] и [М+1, µ, Р] на глубине залегания µ,

в граничной точке [М+2, µ, Р]:

в граничной точке [М+1, µ-1, Р]:

аналогично пересчитывают температуру в оставшихся точках, приборами инфракрасной термографии измеряют избыточные значения температур в интервале времени [τ₁, τ₂], после чего в каждой точке зондируемой поверхности грунта рассчитывают во всем интервале времени измерений дифференциальную термограмму между ее избыточной температурой и средним значением температуры зондируемой поверхности, в точках, в которых дифференциальная термограмма не равна нулю, идентифицируют теплофизические свойства скрытого объекта, для чего используют численную математическую модель, рассчитывают дифференциальную термограмму, полученную для грунта с учетом скрытого объекта и грунта без скрытого объекта:

решают обратную коэффициентную задачу теплопроводности вариационным методом на интервале наблюдения избыточной температуры [τ₁, τ₂], по невязке:

искомые теплофизические свойства скрытого объекта a₂, λ₂ и глубину его залегания µ находят из минимума функции J(a₂, λ₂, µ),

определяют размеры скрытого объекта, глубину залегания, а на основании значения его теплофизических свойств материал классифицируют, зависимость теплофизических свойств от температуры аппроксимируют кусочно-линейной финитной функцией:

где T - температура;

γ=а_i, λ_i при значении избыточной температуры Т=0°С; Т₁=50°С; T₂=80°С; ;

К_ja, К_jλ - линейный коэффициент зависимости теплофизических свойств от температуры ;

а₁ - температуропроводность грунта;

λ₁ - теплопроводность грунта;

а₂ - температуропроводность скрытого объекта;

λ₂ - теплопроводность скрытого объекта;

- сеточная функция;

m, n, р - номер отсчетов для сеточной функции;

k - номер отсчета по времени;

2M×N×2P - размеры моделируемого объема грунта;

h - шаг сетки по расстоянию;

Δτ - шаг сетки по времени;

q - плотность теплового потока, отнесенная к единице площади поперечного сечения пространственной сетки и выраженная в Вт/м²;

α - коэффициент теплоотдачи, отнесенный к единице площади поперечного сечения пространственной сетки и выраженный в Дж/(м²·К);

τ - текущее время, отсчитываемое от момента теплового воздействия;

τ^* - длительность теплового воздействия;

µ - координата глубины залегания скрытого объекта;

J - функционал невязки;

T(τ, а₁, λ₁, а₂, λ₂, µ) - значение избыточной температуры, рассчитанное математической моделью с учетом сеточной модели скрытого объекта;

D(τ, a₂, λ₂, µ) - дифференциальная термограмма на поверхности грунта, рассчитанная математической моделью;

- дифференциальная термограмма на поверхности грунта, измеренная приборами инфракрасной термографии.

Способ осуществляют на основании следующих рассуждений.

Плоскую поверхность грунта нагревают в течение определенного времени тепловым потоком от инфракрасного нагревателя, а с помощью средств инфракрасной термографии измеряют избыточные температуры на плоской поверхности грунта в заданном интервале времени. Данный физический процесс можно описать математической моделью нелинейной задачи теплопроводности с учетом теплообмена грунта с окружающей средой:

T(x₁, x₂, x₃, 0)=0, T(±∞, ±∞, ±∞, τ)→0,

граничные условия:

где Т_n - температура поверхности исследуемого образца; h(τ) - ступенчатая функция, x, y, z - оси правой декартовой прямоугольной системы координат.

Нелинейную задачу теплопроводности (9) при граничных условиях (10) решают методом конечных разностей. Разностная схема для трехмерного уравнения теплопроводности имеет вид (3). Граничные условия аппроксимируют на основании выражения:

полученного с помощью метода теплового баланса. При этом q и α отнесены к единице площади поперечного сечения пространственной сетки и выражены в Вт/м² и Дж/(м²·К).

На подготовительном этапе к зондированию грунта получают две численные математические модели:

- первая математическая модель, моделирующая нелинейное распространение тепла на поверхности грунта при его нагреве тепловым излучением и конвективном обмене с окружающей средой, при этом грунт представляется как изотропный дисперсный материал;

- вторая математическая модель, моделирующая нелинейное распространение тепла на поверхности грунта при его нагреве тепловым излучением и конвективном обмене с окружающей средой с учетом наличия скрытого объекта.

На фиг.1а) представлена пространственная сетка первой и второй математической модели. На фиг.1б), в) представлена пространственная сетка скрытого объекта для второй математической модели.

Для получения первой математической модели выражения (9) и (11) приводят к виду (3) и (1), (2) с учетом (8) и рассчитывают изменения значений избыточных температур на интервале [τ₁, τ₂]. Для получения второй математической модели выражения (9) и (11) приводят к виду (3) и (1), (2), при этом используют уточняющие выражения (8) и (4), (5). На фиг.2 представлены относительные графики, аппроксимирующие зависимость (8): 1 - для температуропроводности в виде a{T)/a(0) при K_1а=-0,001·10^-3, K_2a=-0,01·10^-3, K_3a=-0,05·10^-3; 2 - для теплопроводности в виде λ(T)/λ(0) при K_1λ=0,1·10^-3, K_2λ=4·10^-3, K_3λ=8·10^-3.

При непосредственном зондировании грунта приборами инфракрасной термографии измеряют избыточные значения температур в интервале времени [τ₁, τ₂], после чего в каждой точке зондируемой поверхности грунта рассчитывают во всем интервале времени измерений дифференциальную термограмму между ее избыточной температурой и средним значением температуры зондируемой поверхности, в точках, в которых дифференциальная термограмма не равна нулю, идентифицируют теплофизические свойства скрытого объекта, для чего используют вторую математическую модель, рассчитывают дифференциальную термограмму согласно (6) и на основании невязки (7) идентифицируют теплофизические свойства скрытого объекта и глубину его залегания. Численное решение задачи идентификации теплофизических свойств по невязке (7) производится каким-либо из вариационных методов исчисления.

На фиг.3. показана схема устройства, реализующая предлагаемый способ. Устройство содержит инфракрасный нагреватель 1 и прибор инфракрасной термографии 2. Инфракрасный нагреватель 1 в течении заданного времени τ^* равномерно воздействует по всей площади поверхности грунта 3 размерами 2М×2Р, а с помощью прибора инфракрасной термографии 2 в интервале времени [τ₁, τ₂} во всех точках поверхности грунта 3 размерами 2М×2Р измеряют избыточные значения температур. Для тех точек поверхности грунта, в которых дифференциальная термограмма не равна нулю из-за наличия скрытого под поверхностью грунта объекта 4, решают задачу идентификации теплофизических свойств скрытого объекта и глубину его залегания.

Далее формируют трехмерный образ скрытого объекта во всей области моделируемого участка грунта размерами 2M×N×2P, который состоит из совокупности отдельных точек, для каждой из которых идентифицированы значения теплофизических свойств и глубину залегания скрытого объекта. На фиг.3 показана трехмерная реконструкция скрытого объекта: 1 - моделируемый объем грунта, 2 - реконструированное отображение скрытого объекта, состоящего из отдельных точек моделируемого объема, каждой из которых поставлено в соответствие идентифицированное значение {a₂, λ₂, µ}_i, i - порядковый номер.

На основании трехмерной реконструкции скрытого объекта определяют его размеры и среднюю глубину залегания, а на основании среднего значения его теплофизических свойств классифицируют как металл, пластмасса.

Результаты предварительных экспериментов показали, что при мощности теплового потока 150 Вт/м и времени τ^*=60 сек максимальное значение избыточной температуры для класса теплоизоляционных материалов составляет 50…120°С, что требует необходимость учета нелинейной зависимости изменения ТФС материла от температуры. Так, с ростом температуры теплопроводность увеличивается, а температуропроводность уменьшается, а доля изменения теплофизических свойств может составлять до 10-30% на 100°С избыточной температуры, при этом наилучшая аппроксимация зависимости теплофизических свойств от температуры достигается параболической, экспоненциальной или кусочно-линейной функциями (Платунов Е.С. и др. Теплофизические измерения и приборы. - Л.: Машиностроение, 1986).

Для обеспечения высокой воспроизводимости при каждом измерений на основании закона Ламберта угол наблюдения для металлов должен быть 0…40°, а для диэлектриков в интервале 0…60° (Инфракрасная термогарфия. Основы, техника, применение: Пер. с франц. - М.: Мир, 1988. - С.47). Инфракрасный излучатель должен быть расположен параллельно грунту строго на определенной высоте для обеспечения заданного значения мощности теплового потока.

Для учета возникновения вынужденной конвекции при проведении измерений в полевых условиях коэффициент теплоотдачи может быть записан как функция от скорости ветра (Справочник физических величин / Под ред. проф. Г.А.Рябинина.- СПб., Лениздат; Издательство «Союз», 2001. - С.99).

Задача обнаружения может быть реализована в виде активного устройства или пассивного. В первом случае устройство состоит из инфракрасного нагревателя, который воздействует на участок поверхности и тепловизора, регистрирующего распространение изотерм, при этом чувствительность измерения температуры должна быть не ниже 0.002 K. Во втором случае в качестве нагревателя используется энергия солнца - естественный нагрев земной поверхности, табл.1.

Совмещая работу в пассивном режиме с активным режимом, становится возможным предварительное обнаружение мин с помощью летательного аппарата с минимальным разрешением и дальнейшее уточнение местонахождения с большим разрешением и на большей глубине активным устройством. Обеспечив высокое угловое разрешение оптических систем для многодиапазонных инфракрасных оптико-электронных средств, возможно решение задачи обнаружения скрытых объектов с высот нескольких километров на площадях в несколько десятков квадратных километров.

Таблица 1.
Варианты устройств
Активное устройство	Пассивное устройство	Параметр
на автомоби-ле	носимое	размещение на летательном аппарате	на автомобиле, носимое
1×1 см	0,5×0,5 см	на высоте полета 100 м 20×20 см, на высоте полета 50 м 10×10 см	3×3…5×5 см	минимальные размеры объекта, который возможно обнаружить на глубине 10-20 см
1 мин/м2	1-2 мин/м2	в реальном режиме времени	в реальном режиме времени	время на обнаружение
снежный покров	снежный покров, густая трава	ограничения по применению

В предлагаемом способе обнаружения скрытых объектов (мин) критерием обнаружения является разница значений теплофизических свойств между грунтом и скрытым объектом. Так, теплопроводность металла 15-60 Вт/(м·K), а пластмасс 0,05-0,1 Вт/(м·K), что на один-два порядка больше/меньше теплопроводности грунта 1-1,5 Вт/(м·K). При этом способ позволяет дистанционно идентифицировать как скрытые металлические объекты, так и пластмассовые с указанием глубины их залегания.

Способ идентификации комплекса теплофизических свойств твердых материалов для обнаружения скрытых объектов в грунте, включающий тепловое импульсное воздействие от инфракрасного источника нагрева на плоскую поверхность грунта, измерение избыточной температуры на плоской поверхности грунта в заданном интервале времени, расчет математической модели прямой задачи теплопроводности на основе метода конечных разностей, отличающийся тем, что измерение избыточной температуры производят во всех точках зондируемой поверхности грунта, применяют трехмерную промежуточную сеточную функцию источника нагрева: при трехмерную сеточную функцию на k+1 временном слое: при i=1, рассчитывают численную модель скрытого объекта с теплофизическими свойствами {а₂, λ₂}, расположенного между точками [М-1, µ, P] и [M+1, µ, P] на глубине залегания µ,в граничной точке [М+2, µ, P]: в граничной точке [M+1, µ-1, P]: аналогично пересчитывают температуру в оставшихся точках,приборами инфракрасной термографии измеряют избыточные значения температур в интервале времени [τ₁, τ₂], после чего в каждой точке зондируемой поверхности грунта рассчитывают во всем интервале времени измерений дифференциальную термограмму между ее избыточной температурой и средним значением температуры зондируемой поверхности, в точках, в которых дифференциальная термограмма не равна нулю, идентифицируют теплофизические свойства скрытого объекта, для чего используют численную математическую модель, рассчитывают дифференциальную термограмму, полученную для грунта с учетом скрытого объекта и грунта без скрытого объекта: решают обратную коэффициентную задачу теплопроводности вариационным методом на интервале наблюдения избыточной температуры [τ₁, τ₂], по невязке: искомые теплофизические свойства скрытого объекта а₂, λ₂ и глубину его залегания µ находят из минимума функции J(a₂, λ₂, µ),определяют размеры скрытого объекта, глубину залегания, а на основании значения его теплофизических свойств материал классифицируют,зависимость теплофизических свойств от температуры аппроксимируют кусочно-линейной финитной функцией: где Т - температура;γ=a_i, λ₁, при значении избыточной температуры Т=0°С; Т₁=50°С; T₂=80°С; K_ja, K_jλ, - линейный коэффициент зависимости теплофизических свойств от температуры, а₁ - температуропроводность грунта;λ_i - теплопроводность грунта;а₂ - температуропроводность скрытого объекта;λ₂ - теплопроводность скрытого объекта; - сеточная функция;m, n, p - номер отсчетов для сеточной функции;k - номер отсчета по времени;2M×N×2P - размеры моделируемого объема грунта;h - шаг сетки по расстоянию;Δτ - шаг сетки по времени;q - плотность теплового потока, отнесенная к единице площади поперечного сечения пространственной сетки и выраженная в Вт/м²;α - коэффициент теплоотдачи, отнесенный к единице площади поперечного сечения пространственной сетки и выраженный в Дж/(м²·K);τ - текущее время, отсчитываемое от момента теплового воздействия;τ^* - длительность теплового воздействия;µ - координата глубины залегания скрытого объекта;J - функционал невязки;Т(τ, а₁, λ₁, а₂, λ₂, µ) - значение избыточной температуры, рассчитанное математической моделью с учетом сеточной модели скрытого объекта;D(τ, a₂, λ₂, µ) - дифференциальная термограмма на поверхности грунта, рассчитанная математической моделью; - дифференциальная термограмма на поверхности грунта, измеренная приборами инфракрасной термографии.