Способ моделирования и визуализации распространения возбуждения в миокарде

Способ моделирования и визуализации распространения возбуждения в миокарде

Иллюстрации

Показать все

Реферат

Предлагаемое изобретение относится к медицине, в частности к кардиологии, и может быть использовано в клинических и экспериментальных исследованиях как неинвазивный способ определения статических и динамических показателей миогемодинамики и для наглядного, реалистичного представления функционального состояния сердца человека, а также процесса распространения волны возбуждения в миокарде.

Известен неинвазивный способ определения основных показателей миогемодинамики левого желудочка (ЛЖ) сердца [1], заключающийся в регистрации электрокардиограммы (ЭКГ), измерении информационных параметров ЭКГ и вычислении основных объемно-функциональных показателей миогемодинамики ЛЖ по оригинальным математическим формулам. Однако в известном способе отсутствует вычисление основных объемно-функциональных показателей всего сердца, вычисление основных объемно-функциональных показателей ЛЖ осуществляется без привязки к «геометрии» сердца конкретного человека, то есть результаты обработки кардиографической информации представлены в ненаглядном виде.

Наиболее близким по достигаемому результату к предлагаемому изобретению является способ определения основных функциональных показателей миогемодинамики сердца, заключающийся в регистрации ЭКГ, анализе информационных показателей ЭКГ, регистрации флюорографии, анализе информационных показателей флюорографии, синтезе модели сердца человека и определении показателей миогемодинамики сердца [2].

К недостаткам известного способа определения основных показателей миогемодинамики сердца относится то, что в нем при определении основных показателей миогемодинамики сердца не учитывается процесс распространения возбуждения по сердцу, поэтому полученные показатели миогемодинамики являются статичными и невозможно просмотреть их динамику в течение кардиоцикла.

Действительно, в известном способе эффект достигается только за счет наглядного представления «геометрии» сердца человека. Именно визуализация сердца пациента является принципиальной отличительной особенностью известного способа. В известном способе вычисление основных объемно-функциональных показателей ЛЖ осуществляется с привязкой к «геометрии» сердца конкретного человека, при этом результаты обработки ЭКГ и флюорографии представлены в наглядном виде.

Однако, по мнению авторов, такое представление диагностической информации для оценки состояния сердца пациента является недостаточным. Врачу необходима информация об электрической активности и миогемодинамике сердца в течение кардиоцикла.

Изобретение направлено на расширение функциональных возможностей кардиологического исследования за счет моделирования и наглядного представления распространения возбуждения на модели реалистичного изображения сердца пациента и определения основных показателей миогемодинамики сердца в течение кардиоцикла.

Это достигается тем, что в способ определения основных функциональных показателей миогемодинамики сердца, заключающийся в том, что регистрируют электрокардиограмму и определяют конечный диастолический радиус (КДР) и конечный систолический радиус (КСР) полости ЛЖ, конечный диастолический объем (КДО) и конечный систолический объем (КСО) ЛЖ, которые рассчитываются по данным электрокардиограммы в одном из следующих отведений: 4, 5, 6-м грудном (по Вильсону) или 11 стандартном (по Эйнтховену), выбранном соответственно направлению электрической оси сердца, а при невозможности их регистрации - в отведении А (по Небу), измеряют при отсутствии блокад ножек пучка Гиса продолжительности интервалов QR, RS, QRS, ST-T, R-R и дополнительно при блокаде левой ножки пучка Гиса - продолжительности интервала R₁R₂, а при блокаде правой ножки пучка Гиса - продолжительности интервала S₁S₂, и при синусовом и других наджелудочковых ритмах сердца в состоянии физического покоя определяют по формулам: КДР=(44,5-100·t_RS)·(t_QR+t_RS)-11·t_RS, где t_QR - время от начала зубца Q до вершины зубца R при отсутствии блокады левой ножки пучка Гиса, а при наличии блокады левой ножки пучка Гиса - до первой вершины раздвоенного зубца R(R1), то есть t_QR=t_QR, с; t_RS - время от вершины зубца R до конца зубца S - при отсутствии блокад ножек пучка Гиса, а при блокаде левой ножки пучка Гиса вместо t_RS - разность временных интервалов от первой вершины раздвоенного зубца R до конца зубца S (R1 S) и от первой вершины раздвоенного зубца R до его второй вершины (R₁R₂), то есть , c;

где t_QRS - время комплекса QRS, с; t_ST-T - время от конца зубца S до конца зубца Т - при отсутствии блокад ножек пучка Гиса, а при блокаде левой ножки пучка Гиса вместо t_ST-T - сумма и при блокаде правой ножки пучка Гиса вместо t_ST-T сумма , c;

и далее вычисляют при всех указанных видах сердечного ритма КДО=(4/3)·π·КДР³ и КСО=(4/3)·π·КСР³, а также регистрируют фронтальный и левобоковой флюорографические снимки сердца человека, определяют по снимкам геометрические параметры сердца человека, синтезируют реалистичное трехмерное изображение сердца человека, значения КДР и КСР заменяют реальными эквивалентными геометрическими параметрами модели ЛЖ сердца человека, значения которых определяют по формулам R_i__КДРЛЖ=К_КДР·R_i__модели; R_i__КСРЛЖ=К_КСР·R_i__модели; К_КДР=КДР³/R³ _ср__модели; К_КСР=КСР³/R³ _ср__модели, где R_i__КДРЛЖ - конечное диастолическое расстояние от центра геометрического места точек поверхности модели ЛЖ сердца человека до i-ой точки поверхности модели ЛЖ сердца человека; R_i__КСРЛЖ - конечное систолическое расстояние от центра геометрического места точек поверхности модели ЛЖ сердца человека до i-ой точки поверхности модели ЛЖ сердца человека; R_i__модели - расстояние от центра геометрического места точек поверхности модели ЛЖ сердца человека до i-ой точки поверхности модели ЛЖ сердца человека; R_сф__модели - радиус сферы, объем которой равен объему модели ЛЖ сердца человека; К_КДР, К_КСР - коэффициенты пропорциональности объема модели ЛЖ сердца человека соответственно диастолическому и систолическому объему ЛЖ сердца человека, введены действия, с помощью которых моделируется распространение волны возбуждения в миокарде, затем по результатам моделирования визуализируется распространение волны возбуждения в миокарде и определяются показатели миогемодинамики сердца в процессе распространения волны возбуждения в миокарде соответствующей анатомической части сердца по формуле: где V_i,j - объем полости анатомической части сердца j в i-ый момент времени процесса распространения волны возбуждения в миокарде, КДО_j - конечный диастолический объем полости анатомической части сердца j, КСО_j - конечный систолический объем полости анатомической части сердца j, ψ_i,j - характеристика процесса распространения волны возбуждения в миокарде соответствующей анатомической части сердца, вычисляемая по формуле

,

где S_i,j - площадь возбужденного участка поверхности анатомической части сердца j в момент времени i, S_j - общая площадь поверхности анатомической части сердца j.

При этом моделирование распространения волны возбуждения в миокарде осуществляется на основе модели Алиева-Панфилова путем подбора параметров модели для различных анатомических частей сердца и построения развертки поверхности трехмерной модели сердца человека. Визуализация процесса распространения волны возбуждения миокарда осуществляется средствами компьютерной графики и в наиболее удобном для восприятия виде на основе трехмерной модели сердца пациента.

Введенные действия с их связями проявляют новые свойства, которые позволяют проследить динамику основных показателей миогемодинамики сердца на протяжении одного кардиоцикла, смоделировать и наглядно представить процесс распространения возбуждения в миокарде.

Действительно, моделирование процесса распространения возбуждения в миокарде с учетом анализа кардиографической информации позволит определить изменения электрической активности и миогемодинамики сердца, а визуализация результатов моделирования наглядно представить «электрический портрет сердца» в разные фазы сердечного цикла.

В основе предлагаемого способа лежит представление сердечной мышцы, как проводящей активно-возбудимой среды (АВС) [3, 4]. В АВС каждый элемент обладает собственным источником энергии. В сердечной мышце энергообеспечение клеток миокарда осуществляется в результате последовательного протекания процессов, связанных с выработкой аденозинтрифосфата (АТФ), транспортом энергии от мест образования к местам использования и реализацией сокращения миокарда, а также поддержания ионных градиентов на клеточных мембранах [5]. В АВС каждый элемент может находиться в одном из трех состояний: покой, рефрактерность или возбуждение. Элемент АВС, находящийся в покое, может возбудиться при взаимодействии с соседними элементами. Если же элемент АВС уже возбужден, то соседние элементы не могут дополнительно возбудить его. Состояние рефрактерности (невозбудимости) характерно тем, что элемент нельзя возбудить обычным стимулом. В то же время, если элемент находится в состоянии покоя, он не способен возбудить соседние элементы среды. Волны возбуждения заставляют сердечную мышцу сокращаться и выполнять свою функцию. Автоволна, распространяющаяся в АВС, сохраняет свои характеристики за счет энергии среды. Очевидно, что нарушение распространения автоволн связано с нарушением функционирования в проводящей и мышечной системах сердца, т.е. с различными сердечными патологиями. По мнению авторов, использование автоволнового подхода на основе модели Алиева-Панфилова [6] при моделировании распространения возбуждения в сердце является отличительной особенностью предлагаемого способа.

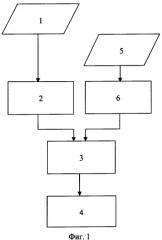
На фигуре 1 приведена блок-схема алгоритма, реализующего известный способ определения основных показателей миогемодинамики сердца. На блок-схеме приняты следующие обозначения:

1 - регистрация ЭКГ;

2 - анализ информационных показателей ЭКГ;

3 - синтез модели сердца человека;

4 - определение показателей миогемодинамики сердца;

5 - регистрация флюорографии;

6 - анализ информационных показателей флюорографии.

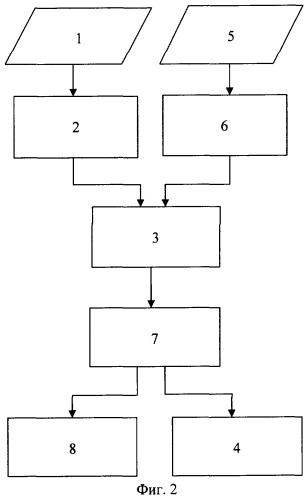
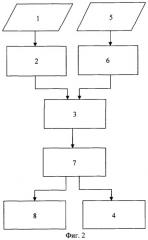
На фигуре 2 приведена блок-схема алгоритма, реализующего предлагаемый способ моделирования и визуализации распространения возбуждения в миокарде. На блок-схеме приняты следующие обозначения:

1 - регистрация ЭКГ;

2 - анализ информационных показателей ЭКГ;

3 - синтез модели сердца человека;

7 - моделирование распространения возбуждения в сердце;

8 - визуализация распространения возбуждения в сердце;

5 - регистрация флюорографии;

6 - анализ информационных показателей флюорографии;

4 - определение показателей миогемодинамики сердца.

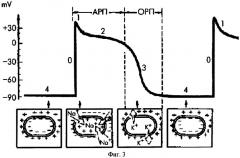
На фигуре 3 приведено изображение формы и фаз трансмембранного потенциала действия (ТМПД) клетки миокарда [7].

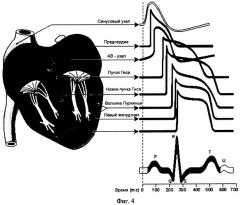
На фигуре 4 приведены формы ТМПД в разных отделах сердца [8].

На фигуре 5 приведена блок-схема алгоритма, реализующего моделирование распространения возбуждения в сердце. На блок-схеме приняты следующие обозначения:

7 - моделирование распространения возбуждения в сердце;

9 - подбор параметров модели Алиева-Панфилова для данного участка сердца;

10 - построение «развертки» поверхности модели сердца пациента;

11 - решение системы уравнений модели Алиева-Панфилова.

На фигуре 6 приведены формы ТМПД, полученные с помощью модели Алиева-Панфилова:

фигура 6а - форма ТМПД в предсердиях;

фигура 6б - форма ТМПД в желудочках.

На фигуре 7 приведено построение цилиндрической проекции сферы [9]:

фигура 7а - проекция сферы на цилиндр;

фигура 7б - цилиндрическая проекция участка сферы А A^I А^II А^III.

На фигуре 8 изображено построение цилиндрической проекции сердца:

фигура 8а - проецирование точек поверхности сердца на боковую поверхность цилиндра;

фигура 8б - цилиндрическая проекция точек («развертка») поверхности модели сердца пациента на сетку решений модели Алиева - Панфилова. На «развертке» приняты следующие обозначения:

1. Область точек предсердий:

1a - область точек правого предсердия;

1б - область точек левого предсердия.

2. Область точек желудочков.

3. Область точек артерий и вен.

На фигуре 9 приведено моделирование распространения возбуждения в течение кардиоцикла.

На фигуре 10 приведено изображение распространения возбуждения в течение кардиоцикла на поверхности модели сердца пациента.

На фигуре 11 изображен шаблон явной двухслойной разностной схемы [10], которая используется при решении системы уравнений модели Алиева-Панфилова.

На фигуре 12 изображены опорные точки поверхности модели сердца человека.

На фигуре 13 изображен результат выполнения триангуляции Делоне [11].

Действительно, как следует из анализа фигуры 2, в предлагаемом способе моделирование распространения возбуждения осуществляется на основе синтезированной модели сердца по данным ЭКГ и флюорографического снимка, а определение показателей миогемодинамики рассчитывается с учетом смоделированного процесса распространения возбуждения.

Суть предлагаемого способа заключается в следующем (см. фигуру 2): первоначально осуществляется регистрация электрокардиографических и флюорографических данных. Затем по данным ЭКГ определяются КСР, КДР, КСО и КДО сердца человека, а на данные флюорографии «накладывается» модель сердца. В результате определяются миогемодинамические показатели сердца человека и «геометрия» сердца человека. Далее определяется объем анатомических частей сердца на его модели КСО_м. Следующим этапом реализации предлагаемого способа является сопоставление объемов сердца человека КСО и модели сердца КСО_м. В результате этого получается модель сердца, полностью повторяющая сердце человека в положении систолы и диастолы.

Далее выполняется моделирование распространения возбуждения в сердце с использованием двухкомпонентной модели Алиева-Панфилова, которая воспроизводит основные свойства волн возбуждения в сердечной мышце [6]. Данная модель представляет собой систему дифференциальных уравнений параболического типа

где ε₀«1, k, α, µ₁, µ₂ - параметры модели.

Для решения данной системы дифференциальных уравнений в частных производных используется метод сеток (метод конечных разностей) [10].

В методе сеток область Ω, в которой необходимо найти решение системы уравнений, разбивается прямыми, параллельными осям t=t_j, x=x_i, у=у_m, х_i=x₀+i·Δx, Δх=(х_n-x₀)/n, i=0, 1, 2, … n, у_m=у₀+m·Δу, Δу=(у_p-у₀)/р, m=0, 1, 2, … р, t_j=t₀+j·Δt, Δt=(t_k-t₀)/k, j=0, 1, 2, … k. Точки, которые лежат на границе Г области Q, называются внешними, остальные - внутренние. Совокупность всех точек называется сеткой Ω, величины Δх, Δу, Δt - шагами сетки по x, у и t соответственно. Идея метода сеток состоит в том, что вместо любой непрерывной функции ω(x,у,t) рассматривается дискретная функция ω_{i, m, j}(x_i, у_m, t_j), которая определена в узлах сетки Ω, а вместо производных функций ω рассматриваются их простейшие разностные аппроксимации в узлах сетки. Таким образом, вместо системы дифференциальных уравнений в частных производных получается система алгебраических уравнений.

Решение проводится по двум пространственным переменным x и у, причем шаги по пространственным осям Δх и Δу равны, т.е. Δx=Δу. В дальнейшем будут использоваться следующие обозначения:

Уравнения системы модели Алиева-Панфилова аппроксимируются разностной схемой, шаблон которой представлен на фигуре 11. При этом производная Δu заменяется приближенной разностной формулой

а производные и :

В результате имеем

Откуда находятся

Данное выражение используется для нахождения переменных u и v модели Алиева-Панфилова для момента времени t+1 с использованием значений, полученных на предыдущем шаге.

Начальные и краевые условия тоже заменяются разностными начальными и краевыми условиями для сеточной функции. Решение системы уравнений находится в некоторой прямоугольной области D плоскости (x,у) (смотрите фигуру 8). Решение производится при заданном начальном условии

и граничных условиях

Пригодность решения, полученного разностной аппроксимацией, требует исследования. Пригодны только такие схемы, в которых при уменьшении шага сетки решение разностного уравнения сходится к решению рассматриваемого дифференциального уравнения. Модель Алиева-Панфилова представляет собой систему дифференциальных уравнений в частных производных параболического типа, поэтому условие устойчивости разностного уравнения будет иметь вид [12]

При моделировании учитывается пространственно-временная организация процесса возбуждения в миокарде. Первоначально проводится моделирование распространения возбуждения в миокарде на плоскости. Для этого поверхность модели сердца проецируется на плоскость, т.е. получается «развертка» поверхности модели сердца пациента на сетку решений модели Алиева-Панфилова (см. фигуру 8). Однако поверхность сердца, как поверхность, гомеоморфную сфере, нельзя развернуть на плоскости без разрыва или смятия. Суть проекции состоит в том, чтобы наилучшим образом «спроектировать» реальную поверхность модели сердца на плоскость, учитывая при этом все искажения и сводя их к минимуму. Главное при построении «развертки» поверхности модели сердца пациента на сетку решений модели Алиева-Панфилова, чтобы каждой исходной точке на поверхности модели сердца пациента соответствовала только одна точка на сетке решений модели Алиева-Панфилова.

Для получения «развертки» поверхности модели сердца пациента используется цилиндрическая проекция [9]. Цилиндрическая проекция является самой распространенной проекцией. Пример построения цилиндрической проекции приведен на фигуре 7. Достоинствами цилиндрической проекции являются равноугольность и небольшие искажения в районе экватора. В цилиндрической проекции меридианы сферы изображаются равноотстоящими параллельными прямыми, а параллели - прямыми, перпендикулярными к изображениям меридианов. Бесконечно малая трапеция А0А'0А''0А'''0 (см. фигуру 7), образованная на поверхности сферы пересечением бесконечно близких друг к другу меридианов и параллелей, на плоскости цилиндрической проекции изобразится прямоугольником АА'А''А''' со сторонами dx и dy. Отрезок А0А'''0 представляет собой бесконечно малую часть меридиана (Rdφ) на сфере, а отрезок А0А'0 представляет собой бесконечно малую часть параллели (rdλ=Rcosφ) на сфере, где r - радиус параллели в широте φ, равный Rcosφ.

Цилиндричность проекции определяет выражение для горизонтальной координаты на проекции: она просто пропорциональна долготе точки λ

x=с(λ-λ0).

Условие равноугольности определяет равенство масштабов по горизонтальной и вертикальной оси. Поскольку масштаб по оси Х на широте φ равен с/(Rcosφ), то из условия dyRcosφ/с=Rdφ получается выражение для зависимости у от φ

Таким образом, посредством цилиндрической проекции осуществляется установление соответствия между каждой точкой поверхности модели сердца с координатами x1, у1, z1 и точкой на двухмерной плоскости с координатами х, у (см. фигуру 8). Так как возбуждение по предсердиям и по желудочкам идет независимо друг от друга, то на плоскости с точками сердца выделяются непроницаемые границы между анатомическими частями сердца (предсердиями и желудочками) путем задания соответствующего граничного условия. Область точек предсердий на фигуре 8(б) обозначена цифрой 1. Область точек желудочков обозначена цифрой 2. Соответственно моделирование распространения возбуждения по предсердиям осуществляется в области 1, а по желудочкам - в области 2.

Для моделирования распространения возбуждения в сердце по результатам анализа ЭКГ представляется информация о временных отсчетах начала и окончания процессов деполяризации и реполяризации анатомических частей сердца, а также информация о поврежденных зонах на поверхности сердца. На основании этих данных корректируются параметры модели Алиева-Панфилова для разных точек поверхности сердца (т.е. моделирование осуществляется в неоднородной возбудимой среде), а также соответствующие начальные условия (распределение трансмембранного потенциала на поверхности сердца в начальный момент времени моделирования). Форма ТМПД в различных анатомических частях сердца различна [7, 8].

В разные фазы ТМПД возбудимость клетки миокарда различна. В начале ТМПД (фаза 0, 1, 2) клетки миокарда полностью невозбудимы (абсолютный рефрактерный период - АРП). Во время быстрой конечной реполяризации (фаза 3) возбудимость частично восстанавливается (относительный рефрактерный период - ОРП). Во время диастолы (фаза 4 ТМПД) рефрактерность отсутствует, и клетка миокарда полностью возбудима (см. фигуру 3).

У клеток предсердий ТМПД имеет крутую фазу деполяризации, максимальное значение трансмембранного потенциала в области пика потенциала действия достигает от +20 до +30 мВ. Затем происходит медленное возвращение трансмембранного потенциала к уровню покоя в течение примерно 200 мс при почти постоянной скорости изменения трансмембранного потенциала. У сократительных клеток желудочков имеется такая же крутая фаза деполяризации, за которой следует первая фаза быстрой реполяризации. При этом мембрана реполяризуется частично - происходит снижение трансмембранного потенциала почти до нулевого уровня. Этот уровень поддерживается примерно в течение 200 мс, т.е. на протяжении фазы плато, за которой следует вторая фаза быстрой реполяризации, или фаза конечной реполяризации, длящаяся также около 200 мс и возвращающая трансмембранный потенциал к уровню потенциала покоя. Скорость изменения трансмембранного потенциала в фазе конечной реполяризации составляет от 0,3 до 0,5 мВ/мс [8].

При моделировании эти особенности ТМПД учитываются путем использования различных наборов параметров в модели Алиева-Панфилова. Возможные формы ТМПД для желудочков и предсердий, полученные в результате моделирования, приведены на фигуре 6.

В результате решения системы уравнений модели Алиева-Панфилова на двумерной плоскости предоставляются данные, описывающие изменение распределения трансмембранного потенциала на поверхности сердца во времени (например, в течение одного кардиоцикла, см. фигуру 9).

Для визуализации процесса распространения возбуждения в сердце используется реалистичное изображение модели сердца человека. Полученное в результате моделирования распределение ТМПД на поверхности сердца накладывается на трехмерную модель сердца (см. фигуру 10). В модели Алиева-Панфилова фактические ТМПД и время могут быть получены по формулам [6]

E[mV]=100u-80,

t[ms]=12,9t[t.u].

Эти формулы используются при расчете изменения ТМПД в любой точке поверхности сердца во времени, а также для определения текущего времени моделирования на ЭКГ.

По результатам моделирования наглядно представляется процесс распространения возбуждения в сердце в течение кардиоцикла (см. фигуру 10).

Определение изменения показателей миогемодинамики сердца в течение кардиоцикла в предлагаемом способе осуществляется следующим образом. Так как сердце является сложным криволинейным объектом, то при его изображении используется следующий подход, традиционный для компьютерной графики: задаются координаты опорных точек, определяющих вид искомой поверхности (см. фигуру 12). Очевидно, что чем больше имеется опорных точек, тем точнее можно восстановить криволинейные участки поверхности. Для аппроксимации поверхности модели сердца используется триангуляция Делоне [11]. Для построения триангуляции точки поверхности соединяют прямыми так, чтобы каждая точка стала вершиной треугольника, а каждый отрезок прямой - стороной треугольника (см. фигуру 13). Триангуляция удовлетворяет условию Делоне, если внутрь окружности, описанной вокруг любого построенного треугольника, не попадает ни одна из заданных точек триангуляции. Таким образом, поверхность модели сердца человека изображается в виде совокупности плоских треугольных граней.

При определении показателей миогемодинамики соответствующей анатомической части сердца в процессе распространения волны возбуждения в миокарде рассматривается отношение площади поверхности возбужденного участка анатомической части сердца к общей площади поверхности анатомической части сердца. Общая площадь поверхности анатомической части сердца определяется как сумма площадей треугольников модели сердца человека, вершины которых принадлежат данной анатомической части сердца. Под площадью возбужденного участка анатомической части сердца понимается сумма площадей треугольников модели сердца человека, принадлежащих данной анатомической части модели сердца человека, причем значение трансмембранного потенциала в вершинах треугольников превышает пороговый уровень. Для клеток сердца пороговый уровень составляет примерно -60 мВ.

Для определения площади треугольника применяется следующий метод. Треугольники в модели сердца человека заданы координатами вершин в трехмерной декартовой системе координат: А(а_х,a_у,a_z), B(b_x,b_у,b_z), C(c_x,с_у,с_z). Координаты векторов и определяются следующим образом:

Площадь треугольника АВС равна половине площади параллелограмма, построенного на векторах и , поэтому находим векторное произведение этих векторов [10]:

Здесь , и - основные вектора или орты.

Следовательно,

или

Определение показателей миогемодинамики сердца в процессе распространения волны возбуждения в миокарде соответствующей анатомической части сердца осуществляется по формуле

где V_i,j - объем полости анатомической части сердца j в i-ый момент времени процесса распространения волны возбуждения в миокарде, КДО_j - конечный диастолический объем полости анатомической части сердца j, KCO_j - конечный систолический объем полости анатомической части сердца j, ψ_i,j - характеристика процесса распространения волны возбуждения в миокарде соответствующей анатомической части сердца, вычисляемая по формуле

,

где S_i,j - площадь возбужденного участка поверхности анатомической части сердца j в момент времени i, S_j - общая площадь поверхности анатомической части сердца j.

Таким образом, в предлагаемом способе на основе реалистичного трехмерного изображения сердца человека, построенного по данным анализа электрокардиографии и флюорографии, осуществляется моделирование и визуализация распространения волны возбуждения в сердце человека, и определяются функциональные показатели миогемодинамики в течение кардиоцикла.

Новые свойства предлагаемого способа позволяют врачу эффективнее оценить состояние сердца пациента.

При этом сохраняются достоинства известного способа по исходной точности измерения сигнала ЭКГ и определению основных функциональных показателей миогемодинамики сердца.

Литература

1. М.Ю.Сафонов. Способ определения основных функциональных показателей миогемодинамики левого желудочка сердца. Патент РФ №2107457, МПК А61В 5/02, 1998.

2. О.Н.Бодин и др. Способ определения основных функциональных показателей миогемодинамики сердца. Патент РФ №2264786, МПК А61В 5/0402, 2005.

3. Ю.Е.Елькин. Волны возбуждения в биологических системах и кинематический подход к их изучению. // В кн. Компьютеры и суперкомпьютеры в биологии / Под ред. В.Д.Лахно и М.Н.Устинина. - Москва-Ижевск: Институт компьютерных исследований, 2002, 528 с., с.247-273.

4. В.Ф.Антонов. Биофизика мембран. // Соросовский Образовательный Журнал, 1996, №6, с.4-12.

5. В.И.Капелько. Нарушение энергообразования в клетках сердечной мышцы: причины и следствия. // Соросовский Образовательный Журнал, 2000, №5, с.14-20.

6. R.R.Aliev, A.V.Panfilov. A simple model of cardiac excitation. // Chaos, Solitons & Fractals, 1996, v.7, №3, p.293-301.

7. Г.Е.Ройтберг, А.В.Струтынский. Внутренние болезни. Сердечно-сосудистая система. М.: ОАО Медицина, 2002.

8. Л.И.Титомир, П.Кнеппо. Математическое моделирование биоэлектрического генератора сердца. М.: Наука, 1999.

9. Л.А.Вахрамеева, Л.М.Бугаевский, З.Л.Казакова. Математическая картография. Учебник для вузов. М.: Недра, 1986.

10. Справочник по математике для научных работников и инженеров. // Корн Г., Корн Т. - М.: Наука. Главная редакция физико-математической литературы, 1984.

11. А.В.Скворцов. Обзор методов построения триангуляции Делоне. // Вычислительные методы и программирование, 2002, Т.3, с.14-39.

12. Уравнения математической физики. Тихонов А.Н., Самарский А.А., Изд. 5-е, стереотипное, учебное пособие для высших учебных заведений. Главная редакция физико-математической литературы издательства «Наука», М., 1977, 736 с.

1. Способ моделирования и визуализации распространения возбуждения в миокарде, заключающийся в том, что регистрируют электрокардиограмму и определяют конечный диастолический радиус (КДР) и конечный систолический радиус (КСР) полости ЛЖ, конечный диастолический объем (КДО) и конечный систолический объем (КСО) ЛЖ, которые рассчитываются по данным электрокардиограммы в одном из следующих отведениий: 4, 5, 6-м грудном (по Вильсону) или 11 стандартном (по Эйнтховену), выбранном соответственно направлению электрической оси сердца, а при невозможности их регистрации - в отведении А (по Небу), измеряют при отсутствии блокад ножек пучка Гиса продолжительности интервалов QR, RS, QRS, ST-T, R-R и дополнительно при блокаде левой ножки пучка Гиса - продолжительности интервала R₁R₂, а при блокаде правой ножки пучка Гиса - продолжительности интервала S₁S₂, и при синусовом и других наджелудочковых ритмах сердца в состоянии физического покоя определяют по формулам КДР=(44,5-100·t_RS)·(t_QR+t_RS)-11·t_RS, где t_QR - время от начала зубца Q до вершины зубца R при отсутствии блокады левой ножки пучка Гиса, а при наличии блокады левой ножки пучка Гиса - до первой вершины раздвоенного зубца R(R1), то есть t_QR=t_QR с; t_RS - время от вершины зубца R до конца зубца S при отсутствии блокад ножек пучка Гиса, а при блокаде левой ножки пучка Гиса вместо t_RS - разность временных интервалов от первой вершины раздвоенного зубца R до конца зубца S (R1S) и от первой вершины раздвоенного зубца R до его второй вершины (R₁R₂), то есть , где t_QRS - время комплекса QRS, с; t_ST-Т - время от конца зубца S до конца зубца Т при отсутствии блокад ножек пучка Гиса, а при блокаде левой ножки пучка Гиса вместо t_ST-Т - сумма и при блокаде правой ножки пучка Гиса вместо t_ST-Т - сумма , с; и далее вычисляют при всех указанных видах сердечного ритма КДО=(4/3)·π·КДР³ и КСО=(4/3)·π·КСР³, а также регистрируют фронтальный и левобоковой флюорографические снимки сердца пациента, определяют по снимкам геометрические параметры сердца пациента, синтезируют реалистичное трехмерное изображение сердца пациента, значения КДР и КСР заменяют реальными эквивалентными геометрическими параметрами модели ЛЖ сердца пациента, значения которых определяют по формулам R_{i_КДРЛЖ}=К_КДР·R_{i_модели}; R_{i_КСРЛЖ}=К_КСР·R_{i_модели}; К_КДР=КДР³/R³ _{сор_модели}; К_КСР=КСР³/R³ _{ср_модели}, где R_{i_КДРЛЖ} - конечное диастолическое расстояние от центра геометрического места точек поверхности модели ЛЖ сердца пациента до i-й точки поверхности модели ЛЖ сердца пациента; R_{i_КСРЛЖ} - конечное систолическое расстояние от центра геометрического места точек поверхности модели ЛЖ сердца пациента до i-й точки поверхности модели ЛЖ сердца пациента; R_{i_модели} - расстояние от центра геометрического места точек поверхности модели ЛЖ сердца пациента до i-й точки поверхности модели ЛЖ сердца пациента; R_{сф_модели} - радиус сферы, объем которой равен объему модели ЛЖ сердца пациента; К_КДР, К_КСР - коэффициенты пропорциональности объема модели ЛЖ сердца пациента соответственно диастолическому и систолическому объему ЛЖ сердца пациента, отличающийся тем, что моделируется распространение волны возбуждения в миокарде, затем по результатам моделирования визуализируется распространение волны возбуждения в миокарде и определяются показатели миогемодинамики сердца в процессе распространения волны возбуждения в миокарде соответствующей анатомической части сердца по формуле где V_i,j - объем полости анатомической части сердца j в i-й момент времени процесса распространения волны возбуждения в миокарде, КДО_j - конечный диастолический объем полости анатомической части сердца j, KCO_j - конечный систолический объем полости анатомической части сердца j, ψ_i,j - характеристика процесса распространения волны возбуждения в миокарде соответствующей анатомической части сердца, вычисляемая по формуле ,где S_i,j - площадь возбужденного участка поверхности анатомической части сердца j в момент времени i, S_j - площадь поверхности анатомической части сердца j.

2. Способ по п.1, отличающийся тем, что моделирование распространения волны возбуждения в миокарде осуществляется на основе модели Алиева-Панфилова путем подбора параметров модели для различных анатомических частей сердца и построения развертки поверхности трехмерной модели сердца пациента.

3. Способ по п.1, отличающийся тем, что визуализация процесса распространения волны возбуждения миокарда осуществляется средствами компьютерной графики в реальном времени и наиболее удобном для восприятия виде на основе т