Устройство визуализации теплопроводности ферромагнетиков

Устройство визуализации теплопроводности ферромагнетиков

Иллюстрации

Показать все

Реферат

Изобретение относится к области физики и может быть использовано для демонстрации процесса теплопроводности в ферромагнетиках, помещенных в магнитное поле.

Известно, что магнитная восприимчивость χ ферромагнетиков, как правило, существенно зависит от температуры и определяется законом Кюри (1885) χ=С_т/Т, где С_т - постоянная Кюри, Т - температура. Эта формула была получена П.Ланжевеном (1905), рассмотревшим задачу о намагничивании газа, обладающего магнитным моментом. В квантовой теории парамагнетизма, развитой Д.Ван Флеком (1928-32), значение постоянной Кюри определяется величинами квантовых чисел - спинового , орбитального - и полного - моментов магнитного иона и зависит от соотношения расщеплений уровней энергии иона в результате спин-орбитального взаимодействия и действия внутрикристаллического поля. При учете указанного взаимодействия закон Кюри переходит в закон Кюри-Вейсса. Связанные с этим законом отклонения от закона Кюри всегда наблюдаются при достаточно низких температурах.

Температурная зависимость магнитной восприимчивости χ парамагнетика, установленная Вейссом (1907), по закону Кюри-Вейсса имеет вид χ=С_т/(Т-Θ), где Θ - температура Кюри. Было показано, что у очень многих ферро- и антиферромагнетиков в парамагнитной области (при температурах соответственно выше точки Кюри Тс и выше точки Нееля Т_N) зависимость χ(Т) определяется законом Кюри. У ферромагнетиков Θ>0, у антиферромагнетиков Θ<0. В монокристаллах Θ анизотропна, этот эффект достигает большой величины в редкоземельных металлах. Выполнение закона Кюри-Вейсса в широком интервале температур носит приблизительный характер (Ч.Киттель, Введение в физику твердого тела. Пер. с англ., М., 1978; Т.Мория, Последние достижения теории магнетизма коллективизированных электронов. Пер. с англ., УФН, 1981, т.135, с.117).

В ферромагнитных веществах в областях, превышающих точку Кюри, магнитная восприимчивость сильно уменьшается с ростом температуры. Это обстоятельство положено в основу действия рассматриваемого устройства, использующего так называемый магнитотермомеханический эффект (МТМ-эффект), сущность которого состоит в возникновении механической силы, приложенной к объему пара- или ферромагнитного вещества с изменяющейся от температуры магнитной восприимчивостью, помещенного в магнитное поле и находящегося в термодинамически неравновесном состоянии, причем вектор этой силы направлен коллинеарно с вектором градиента температуры. МТМ-эффект объясняется возникновением градиента магнитной восприимчивости пара- или ферромагнитного вещества в направлении, противоположном направлению градиента температуры в нем, в результате чего «центр тяжести» намагниченности вещества смещается относительно центра притяжения действующего на него магнитного поля в направлении градиента магнитной восприимчивости.

Аналоги заявляемого технического решения отсутствуют.

Целью изобретения является визуализация процесса теплопроводности в ферромагнетике, в частности, скорости движения в нем тепловой энергии как функции градиента температуры в ферромагнетике, помещенном в однородное (или неоднородное) магнитное поле.

Указанная цель достигается в заявляемом техническом решении - устройстве визуализации теплопроводности ферромагнетиков, состоящем из исследуемого ферромагнетика, выполненного, например, в форме подвижного кольца, отрезок которого L помещен в зазор магнитного поля, с одной стороны которого ферромагнетик нагревается до температуры Т₂ электронагревательным элементом, подключенным через понижающий трансформатор с регулируемым по напряжению источником переменного тока, а с другой - охлаждается до температуры T₁<Т₂, например, потоком воздуха с помощью диффузора с компрессором.

Достижение указанной цели объясняется возникновением градиента температуры на отрезке L ферромагнитного кольца, равного grad Т=(T₂-T₁)/L, что вызывает соответствующее перераспределение магнитной восприимчивости ферромагнитного вещества на отрезке L, находящемся в постоянном однородном (или неоднородном) магнитном поле. Это перераспределение приводит к рассредоточению центра намагниченности ферромагнетика на указанном его отрезке L и центра магнитного притяжения в указанном магнитном поле и, следовательно, к возникновению силы, стремящейся эти центры сблизить. Данная сила направлена вдоль вектора градиента температуры в ферромагнетике. При установке кольцевого ферромагнетика на скользящей основе, например на трех направляющих колесах, действие указанной силы приведет к вращению кольцевого ферромагнетика с линейной скоростью внутри магнитного зазора, равной скорости распространения тепловой энергии в теле кольцевого ферромагнетика. Указанная сила пропорциональна квадрату напряженности магнитного поля в зазоре постоянного магнита, она вызывает вращательный момент, величина которого должна превышать момент трения указанной выше скользящей основы (иначе движение ферромагнитного кольца невозможно).

Изобретение понятно из представленных чертежей.

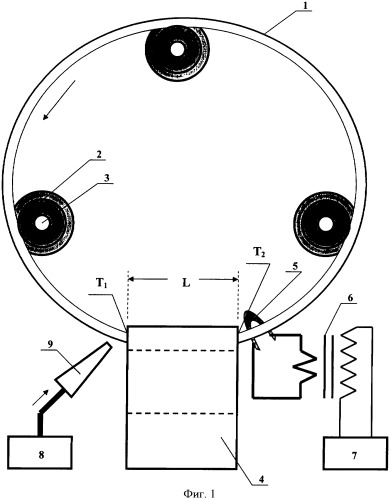
На фиг.1 изображена схема заявляемого устройства. Оно состоит из ферромагнитного кольца 1, установленного на скользящей основе из трех направляющих колес 2 с осями их вращения 3, и постоянного магнита 4, в магнитном зазоре которого длиной L размещена часть ферромагнитного кольца. С одной стороны магнитного зазора в непосредственной близости от ферромагнитного кольца установлен электронагревательный элемент 5, подключенный через понижающий трансформатор 6 к регулируемому по напряжению источнику переменного тока 7. С другой стороны магнитного зазора установлен холодильник, выполненный из компрессора 8 и воздушного диффузора 9, обеспечивающих воздушное охлаждение ферромагнитного кольца.

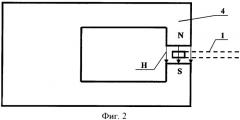
На фиг.2 представлен вид на постоянный магнит 4 с ферромагнитным кольцом 1 в магнитном зазоре.

На фиг.3 дан вид сбоку-изнутри ферромагнитного кольца 1, находящегося в магнитном зазоре длиной L постоянного магнита 4.

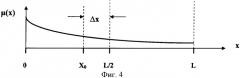
На фиг.4 приведен график распределения относительной магнитной проницаемости µ(x) вдоль координаты x с указанием на рассредоточение центра намагничения ферромагнитного кольца на его отрезке L с координатой х=Х₀ и центра притяжения в магнитном зазоре постоянного магнита с координатой x=L/2 (для однородного магнитного поля в зазоре), и при этом L/2>Х₀.

На фиг.5 представлены графики температурной зависимости относительной магнитной проницаемости µ(T) двух различных ферромагнетиков - никеля Ni и диспрозия Dy.

Рассмотрим действие заявляемого технического решения.

Электронагревательный элемент 5, находящийся в тепловом контакте с ферромагнитным кольцом 1, нагревает последний с одной стороны магнитного зазора постоянного магнита 4 до температуры T₂, а направленным потоком воздуха с помощью компрессора 8 и диффузора 9 ферромагнитное кольцо 1 с другой стороны магнитного зазора охлаждается до температуры T₁, что приводит к возникновению градиента температуры на длине L ферромагнитного кольца величиной grad Т=(Т₂-T₁)/L, что обусловливает движение тепловой энергии в теле ферромагнитного кольца в направлении от более горячего поперечного слоя к более холодному поперечному слою. Скорость этого невидимого движения тепловой энергии определяется уравнением теплопроводности и возрастает с увеличением градиента температуры. Если ферромагнитное кольцо выполнено, например, из никеля, термомагнитная характеристика которого представлена на фиг.5, ясно, что с ростом температуры ферромагнетика-никеля уменьшается его относительная магнитная проницаемость. Следовательно, центр намагниченности отрезка L ферромагнитного кольца смещается от его центра (х=L/2) в сторону более холодного слоя (слева от магнитного зазора на фиг.1). При этом координата Х₀ центра намагниченности этого участка ферромагнитного кольца находится из решения интегрального уравнения:

Каждый из интегралов уравнения (1) представляет собой площадь, ограниченную кривой µ(x) и осью абсцисс. При этом очевидно, что Х₀<L/2. Это и является основанием считать, что возникающая сила F притяжения массы ферромагнитного кольца 1 на его участке длиной L к центру магнитного поля (центру притяжения) с координатой х=L/2 направлена к этому центру и F>0. При радиусе ферромагнитного кольца R возникающий в этом кольце вращательный момент М_вр=FR будет приводить ферромагнитное кольцо во вращательное движение при условии, что момент трения

М_тр основания скольжения (из трех направляющих колес 2 и их осями вращения 3) оказывается меньше вращательного момента М_вр. Разностный момент ΔМ=М_вр-М_тр приводит ферромагнитное кольцо во вращение с угловым ускорением ε=ΔМ/I_к, где I_к=m(R²+r²)/4 - момент инерции ферромагнитного кольца, m - полная масса всего кольца, r и R - соответственно внутренний и наружный радиусы ферритового кольца. По мере сближения центров намагниченности и притяжения (уменьшения отрезка ΔХ на фиг.4) в динамике вращения ферромагнитного кольца сила F(Δx) уменьшается по линейному закону: F(Δx)=FΔx/((L/2)-Х₀]. Это означает, что по мере сближения указанных центров выравниваются вращательный момент М_вр(Δх_ост) и момент трения М_тр, где Δх_ост - остаточная ошибка регулирования, величина которой определяется из выражения:

В соответствии с выражением (2) ясно, что ферромагнитное кольцо 1 внутри магнитного зазора постоянного магнита 4 должно переместиться при сохранении температурного распределения µ(x) в отрезке ферромагнитного кольца длиной L на величину:

После перемещения ферромагнитного кольца в новом отрезке L ферромагнитного кольца на величину ξ аналогичное первоначальному распределению температуры будет достигнуто через некоторое время Δt, определяемое скоростью движения тепловой энергии в ферромагнитном кольце, что позволяет считать, что указанная скорость ν_т равна:

Поскольку постоянная времени процесса втягивания ферромагнитного кольца 1 в магнитное поле постоянного магнита 4 существенно меньше постоянной времени распространения теплового поля, определяемой теплопроводностью, то в установившемся режиме центр намагниченности всегда отстает от центра притяжения на величину остаточной ошибки ξ из уравнения (3) и при этом ферромагнитное кольцо будет продвигаться относительно магнитного зазора неподвижно закрепленного постоянного магнита 4 со скоростью ν_т, определяемой в (4). Угловая скорость вращения ферромагнитного кольца будет равна Ω=2ν_т/(R+r).

При изменении напряженности магнитного поля Н в магнитном зазоре постоянного магнита 4 соответственно изменяется величина силы втягивания F, однако это не влияет на величину угловой скорости вращения Ω ферромагнитного кольца, а лишь приводит к изменению остаточной ошибки ξ регулирования (при сохранении условия ΔМ>0).

Можно показать, что сила втягивания определяется формулой:

где ψ=dµ/dT - функция температурной зависимости относительной магнитной проницаемости ферромагнетика, В=µ₀µ(x)Н - магнитная индукция в ферромагнетике, расположенном в магнитном зазоре постоянного магнита 4, µ₀=1,256·10^-6 Гн/м - абсолютная магнитная проницаемость вакуума, W - энергия магнитного поля, запасенная в объеме V ферромагнетика при V=Lq, где q - поперечное сечение ферромагнитного кольца 1, k - безразмерный коэффициент характеризует сам процесс преобразования тепловой энергии, создаваемой электронагревательным элементом 5 в механическую в МТМ-эффекте.

Кратко рассмотрим передачу тепловой энергии в ферромагнитном кольце 1.

Пусть дано изотропное тело: Т - температура тела, ρ - его плотность, γ - удельная теплоемкость, G - интенсивность источников тепла, то есть количество тепла, выделяемого единицей объема тела в единицу времени. Подсчитаем баланс тепла в единицу времени частиц тела, заполняющих объем V. В соответствии с гипотезой Фурье, согласующейся с опытом, количество тепла, поступающего в V через элемент поверхности Δq тела, определяется формулой:

где λ - положительный коэффициент пропорциональности, характеризующий свойства тела и называемый коэффициентом теплопроводности. Следовательно, количество тепла, поступающего в V через поверхность (в нашем случае фиг.1 под величиной надо понимать поперечное к градиенту температуры сечение ферромагнитного кольца, связанной с магнитным полем постоянного магнита, обращенное к нагревателю, создающему в установившемся режиме в этом сечении температуру Т₂), в соответствии с формулой Остроградского будет равно

Общее количество тепла, поступающего в V, определяется равенством

где второе слагаемое в правой части (8) - тепло, поступающее за счет его источников.

Для повышения температуры элемента объема dv на величину dT за время Δt потребуется количество тепла

Общее количество тепла, идущего на повышение температуры частиц тела, заполняющих объем V, в единицу времени будет

Приравнивая (8) и (10), имеем

Учитывая, что область V произвольная, по теореме о среднем значении получаем

Равенство (12) представляет собой дифференциальное уравнение распространения тепла в неоднородном теле. В случае однородного тела, как в случае схемы фиг.1, это уравнение запишется в виде

и представляет собой основное уравнение математической физики - уравнение теплопроводности. В частности, если тепловой поток является стационарным, то есть не зависит от времени, это уравнение будет уравнением Пуассона, и если при этом источники тепла отсутствуют, - уравнением Лапласа.

В нашем случае расчет осложняется тем, что ферромагнитное кольцо вращается, и решение сводится к задаче с переменными параметрами. Кроме того, один конец участка L ферромагнитного кольца связан с источником тепла G, а другой - с холодильником, отнимающим запасаемую в рабочей части кольца тепловую энергию (в установившемся режиме около - G), что также должно соответственно учитываться при решении уравнения теплопроводности. При этом задача решается аналогично решению задачи о диффузии частиц среды, например жидкости, из мест большей концентрации к местам малой концентрации, понимая при этом под концентрацией функцию Т=dQ/dv.

Решение задачи теплопередачи в случае вращающегося ферромагнитного кольца сложно, и этот частный вопрос выходит за рамки данной заявки. Важно лишь отметить, что при заданных параметрах системы (величине магнитной индукции, геометрии ферромагнитного диска, дифференциальной магнитной восприимчивости и коэффициента теплопроводности кольца) можно в принципе строго решить задачу преобразования энергии и найти величину установившейся угловой скорости ферромагнитного кольца, определяемой однозначно скоростью теплового потока в нем.

Таким образом, темп вращения ферромагнитного кольца в точности соответствует средней скорости движения теплового потока в отрезке L ферромагнитного кольца, находящегося в магнитном зазоре постоянного магнита 4. Это означает, что невидимое движение теплового поля в ферромагнитном кольце от источника тепла к холодильнику в заявляемом техническом решении визуализируется в виде синхронного с движением теплового поля вращения ферромагнитного диска. Регулировка напряжения в электронагревательном элементе 5 приводит к изменению скорости вращения ферромагнитного кольца.

1. Устройство визуализации теплопроводности ферромагнетиков, состоящее из исследуемого ферромагнетика, выполненного в форме подвижного кольца, отрезок которого L помещен в зазор магнитного поля, с одной стороны которого ферромагнетик нагревается до температуры Т₂ электронагревательным элементом, подключенным через понижающий трансформатор с регулируемым по напряжению источником переменного тока, а с другой - охлаждается до температуры T₁<T₂.

2. Устройство визуализации теплопроводности ферромагнетиков по п.1, отличающееся тем, что предусмотрено использование диффузора с компрессором для охлаждения ферромагнетика потоком воздуха.