Способ измерения локальных эффективных поверхностей рассеяния объектов в сверхширокой полосе частот

Способ измерения локальных эффективных поверхностей рассеяния объектов в сверхширокой полосе частот

Иллюстрации

Показать все

Реферат

Изобретение относится к радиолокации, в частности к радиолокационным измерениям, и может быть использовано для измерения локальных эффективных поверхностей рассеяния (ЭПР) радиолокационных объектов в сверхширокой полосе частот в свободном пространстве при использовании импульсных сверхширокополосных (СШП) сигналов без несущей, у которых рабочая полоса Δf и средняя частота f₀ сравнимы по величине.

Частотной характеристикой рассеяния объекта может служить интегральная ЭПР цели. Под интегральной ЭПР понимается отношение квадратов амплитуд электрических составляющих падающего Е_П и рассеянного целью стационарного гармонического электромагнитного поля Е_Р с частотой f, измеренного в точке наблюдения на расстоянии R от цели. Если частота электромагнитного поля f изменяется или облучение проводится полем, обладающим энергетическим спектром , а измеряется энергетический спектр рассеянного поля , то получают зависимость интегральной ЭПР от частоты f:

где множитель 4πR² вводится для компенсации затухания рассеянного поля в зоне измерения;

R - расстояние от антенн до объекта.

Интегральные энергетические спектры радиолокационных объектов, рассчитанные частотными методами или преобразованием Фурье временного отклика отраженного от цели сигнала, не позволяют определить локальные ЭПР объекта, так как в них отсутствует информация о взаимном расположении во времени гармоник, образующих импульсный отклик цели на нестационарное возбуждение. При этом локальность ЭПР подразумевает возможность представления отраженного от объекта сигнала сложной формы суперпозицией импульсных характеристик (ИХ) отдельных его элементов («блестящих точек»). Представление ИХ объекта суперпозицией ИХ элементарных рассеивателей обосновано линейностью измерительной системы и линейностью процесса отражения электромагнитной волны от объекта. Возможность декомпозиции ИХ является основанием для моделирования ЭПР объекта сложной формы суперпозицией локальных ЭПР элементарных отражателей объектов. Таким образом, локальные ЭПР объекта могут быть определены по формуле (1) при условии использования в числителе формулы локальных энергетических частотных спектров откликов от «блестящих точек» объекта. Зависимость локальной ЭПР от частоты (отношение энергетических частотных спектров) называют локальной ЭПР радиолокационного объекта и можно обозначить как σ_L(f) или ЭПР_ЛОК(f).

Известен способ измерения ЭПР объектов с малым уровнем отражения [А.С. № 843556, МПК⁷: G01S 13/00, 1979], заключающийся в формировании поля облучения в рабочем объеме радиолокационной установки и размещении в объеме, стробируемом по дальности дополнительного отражателя, жестко закрепленного на подвижной платформе и перемещающегося таким образом, чтобы при определенном положении отражателя векторная сумма радиолокационных сигналов, наведенных в приемопередающей антенне в отсутствие объекта, была равна нулю, Способ по своей сути тождественен компенсации остаточных отражений, производимой в приемном устройстве при отсутствии цели в рабочем объеме. Однако компенсация фоновых отражений не исключает влияние источников помеховых сигналов на суммарное поле облучения и измеренные значения ЭПР объектов.

Известен способ измерения ЭПР объектов, включающий формирование поля облучения в рабочем объеме измерителя, помещение в него исследуемого объекта, измерение рассеиваемой мощности и эталонирование уровней отражаемых радиолокационных сигналов [Комплекс Rat Scat для измерения радиолокационного поперечного сечения целей, ТИИЭР, т.53 № 8, 1965, стр.1085-1094]. Недостатком способа является низкая точность измерения ЭПР объектов из-за отсутствия данных об истинном распределении локальных источников вторичного излучения на трассе распространения электромагнитных волн. Указанный способ измерения ЭПР, вследствие значительных флуктуации фоновых отражений, не обеспечивает постоянства параметров поля облучения в рабочем объеме радиолокационного устройства и контроля точности измерений ЭПР, особенно при малом уровне отражаемых радиолокационных сигналов.

Известен способ [Россия, патент № 2210789, МПК⁷: G0IS 13/00, G01R 29/00, 20082003] измерения эффективной площади рассеяния объектов, позволяющий по измеренной диаграмме ЭПР двух всенаправленных эталонных отражателей, один из которых установлен неподвижно, а другой перемещают в пределах рабочего объема радиолокационного измерительного комплекса (РИК) по заданному закону, определить местоположения и интенсивности локальных неоднородностей, создающих помеховые отражения и приводящих к искажению поля облучения РИК, и устранить их влияние. Способ предназначен для использования на радиолокационных измерительных комплексах открытого и закрытого типа. При его применении точность определения ЭПР объектов может быть повышена в максимумах диаграмм ЭПР на 0,5…2 дБ, а в относительных минимумах - до 10 дБ.

Недостатком всех вышеперечисленных способов является возможность измерения только интегральной ЭПР. Отраженный сигнал формируется всей поверхностью радиолокационного объекта и не удается выделить наиболее отражающие конструктивные элементы - локальные центры отражения, которые и формируют «блестящие точки», определяющие основной вклад в ЭПР объекта. Кроме того измерения проводят не в сверхширокой и даже не в широкой полосе частот, а на фиксированных частотах или, в лучшем случае, используют узкополосные сигналы. Соответственно, информативность этих способов низка.

Наиболее близким по технической сущности к заявляемому способу является способ измерения ЭПР объектов, изложенный в патенте России № 2305852 от 10.09.2007, МПК⁷: G01S 13/00. Для лучшего понимания заявляемого изобретения необходимо подробно рассмотреть сущность способа-прототипа, которая заключается в следующем. Передатчик формирует зондирующий сигнал, который через передающую часть антенны излучается в направлении объекта и путем соответствующей настройки 1/5 части элементов антенны облучает объект. Приемная часть антенны, состоящая из остальных 4/5 элементов, подключенных с возможностью фазирования таким образом, что ДН приемной антенны сужается в узкий пучок, который с помощью блока фазирования и управления может перемещаться по поверхности объекта. Перед проведением измерений, исходя из размеров рабочей зоны и диаметра пучка, для заданной длины волны вычисляется матрица фазовых сдвигов, обеспечивающих фокусирование луча. Отраженный сигнал поступает в приемник, усиливается и проходит в блок оценки ЭПР, который вычисляет значение ЭПР локальных центров отражения путем сравнения с эталонным сигналом, введенным в память блока. Мешающие отражения от посторонних предметов (опор и устройства вращения объекта) предварительно записываются в результате обзора пространства измерений и запоминаются в блоке оценки ЭПР, затем с помощью блока компенсации подаются в противофазе с соответствующей амплитудой от передатчика на вход приемника.

К недостаткам способа-прототипа следует отнести:

1. Низкую точность измерения локальных ЭПР, обусловленную непостоянной разрешающей способностью по дальности из-за невозможности одинаково достаточно точно сфокусировать зондирующий сигнал во всех точках объекта при сканировании антенной решеткой;

2. Сложность аппаратной реализации способа (антенная решетка состоит из 2850 элементов при сфокусированности зондирующего поля на расстояние 15 метров и при угле сканирования 40°);

3. Недопустимо длительное время проведений измерений при работе в широком или сверхшироком диапазоне частот, так как антенная система и блок компенсации должны перестраиваться всякий раз при изменении рабочей частоты. Заявляемое техническое решение свободно от этих недостатков.

Заявляемое техническое решение выгодно отличается от способа - прототипа:

1. Повышенной точностью определения локальных ЭПР исследуемого объекта за счет использования в качестве зондирующего сигнала последовательности сверхкоротких импульсов, имеющих сверхширокий частотный спектр и, соответственно, постоянно высокую разрешающую способность по дальности;

2. Простой реализацией измерительной схемы (см. далее по тексту).

3. Не перестраиваемой в сверхширокой полосе частот антенной системой, излучающим генератором и регистрирующей аппаратурой. Процесс измерений осуществляется за короткий отрезок в реальном масштабе времени.

Технический результат, на получение которого направлено изобретение:

- повышение точности измерения локальных ЭПР объектов за счет высокой разрешающей способности по дальности, присущей сверхкоротким импульсным зондирующим сигналам, а также, за счет временной локализации спектральных компонент отраженного сигнала, получаемой частотно-временной обработкой и предварительным определением локальных энергетических частотных спектров центров рассеяния в полосе частот зондирующего электромагнитного поля;

- сокращение времени определения локальных ЭПР объектов при одновременном упрощении технической реализации заявляемого способа;

- измерение локальных ЭПР того или иного рассевающего центра объекта не на одной из частот, а одновременно в сверхширокой полосе частот.

Технический результат достигается тем, что радиолокационный объект облучают последовательностью сверхкоротких импульсов, измеряют временную зависимость e_П(t) зондирующего сигнала в точке облучения объекта на расстоянии R от антенн. Аппроксимируют эту зависимость вейвлетом и находят численные значения его параметров w и z. Используя преобразование Фурье временной зависимости e_П(t), в точке облучения объекта определяют энергетический частотный спектр зондирующего поля G_П ²(f). Далее, регистрируют временной сигнал, отраженный от объекта u(t) и в базисе найденного аппроксимирующего вейвлета вычисляют энергетический вейвлет-спектр G²(a, b)=|с(а, b)|² коэффициентов вейвлет-преобразования отраженного сигнала. На вейвлет-спектрограмме энергетического спектра в координатах параметров масштаба а≡1/f (f - частота) и сдвига b≡t (t - время) определяют значения параметров масштаба а_maxj и сдвига b_j, соответствующих максимуму отраженной энергии , обусловленному j-м локальным центром рассеяния («блестящей точкой»). Для сечения энергетического вейвлет-спектра b_j отраженного сигнала исследуемой j-й «блестящей точки» вычисляют локальный энергетический спектр коэффициентов вейвлет-преобразования Определяют частоту f_0j как среднюю частоту вейвлета с параметрами w и z и параметрами масштаба и сдвига b_j исследуемой «блестящей точки». По формуле определяют диапазон частот исследуемого локального энергетического частотного спектра и определяют локальный энергетический частотный спектр j-й «блестящей точки». Определяют локальную ЭПР исследуемого локального центра рассеяния объекта по формуле

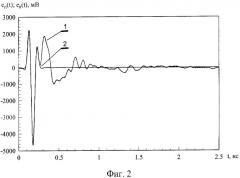
Рассмотрим более подробно предлагаемый способ нахождения локальных ЭПР в сверхширокой полосе частот. Короткий импульс, в котором заключена наибольшая энергия зондирующего сигнала e_П(t) (график 1, фиг.2) в точке облучения объекта с минимально возможной невязкой аппроксимируют подобранным комплексным вейвлетом Морле e_В(t) (график 2, фиг.2) и находят численные параметры w=3,7 и z=0,8 аппроксимирующего вейвлета. В базисе этого вейвлета с найденными параметрами w и z в дальнейшем проводят анализ всех исследуемых отраженных от объектов сигналов. Заявленный способ измерения локальных ЭПР с помощью вейвлет-обработки временного отклика отраженного от объекта СШП сигнала иллюстрируется на примере нахождения локальных ЭПР эталонного отражателя - металлической сферы диаметром D=14,2 см. Этот выбор обусловлен симметрией сферы и наличием для нее строгого решения задачи рассеяния электромагнитного (ЭМ) поля [Кобак В.О. Радиолокационные отражатели. М., «Сов. Радио» 1975, с.101]. По определению ИХ есть реакция измерительной системы на дельта-импульс, т.е. на импульс, с бесконечной полосой частот. На практике исследователь использует импульсы, имеющие ограниченный частотный спектр, и может оценивать только сглаженную ИХ, ширина полосы частот которой определяется спектром зондирующего импульсного сигнала и параметрами приемопередающего тракта измерительной радиолокационной установки. При изменении формы импульса генератора, параметров приемопередающего тракта, соотношения апертур антенн, временная зависимость зондирующего поля (фиг.3, график 1) и отраженный сигнал от сферы (фиг.3, график 2) будут видоизменяться. Соответственно, будет вынужден измениться аппроксимирующий вейвлет и его параметры w и z. Из-за отличий временной зависимости зондирующего поля от дельта-импульса, а также отличий ИХ используемого в эксперименте измерителя от ИХ неискажающего звена, конечной полосы рабочих частот антенн и воздействия шума в тракте приемника, зависимость энергетического частотного спектра облучающего объект сигнала С_П ²(f) (фиг.4) имеет примерно постоянное значение только в ограниченной полосе частот.

В предлагаемом способе возможен учет временной локализации спектральных компонент, т.е. используется частотно-временной подход к исследованию отраженного сигнала. Вейвлет-преобразование отраженного сигнала от сферы u_СФ(t) (фиг.3, график 2) переводит двумерный отраженный временной сигнал от сферы в более эффективное, с позиций обработки, трехмерное частотно-временное изображение РР_ab (фиг.5) или плоское изображение с нанесением линий уровня амплитуды (фиг.6) энергетического вейвлет-спектра. На приведенных фиг.5, 6 явно различимы две блестящие точки. Одна из них, более интенсивная блестящая точка 1, обусловлена зеркальной компонентой рассеяния ЭМ волны от сферы. Другая блестящая точка 2 обусловлена ползущими дифрагирующими ЭМ волнами, огибающими сферу и отражающимися от ее обратной поверхности. Обработка изменяющегося во времени отраженного сигнала u_СФ(t) производится в базисном пространстве найденного ранее аппроксимирующего вейвлета. Для обработки результатов измерений выбиралось максимальное число дискретных точек N=2048; диапазон ранжированной переменной k=0÷N-1. При этом условии, отраженный сигнал u_СФ(1) можно записать как u_СФ(k). Для обработки экспериментальных данных использована комплексная вейвлет-функция Морле (Morlet's wavelet) как наиболее подходящая по форме для аппроксимации электрической компоненты зондирующего поля e_П(k) c наименьшей невязкой. Аналитическая запись этой функции определяется как произведение двух экспонент

где

w=3,7, z=0,8 - параметры найденного аппроксимирующего вейвлета.

С учетом параметров масштаба и сдвига вейвлет может быть записан

где а - параметр масштаба;

b - параметр сдвига.

При обработке полученных в эксперименте сигналов

время дискретизации: t_k=0.001221 нс;

диапазон изменения параметра масштаба: а=0÷200;

диапазон изменения параметра сдвига: b=0÷2048;

время: t_j=t_k·b_j=t_k·k_j;

расстояние распространения ЭМ волны в прямом и обратном направлениях: L=15·t_k·k_j=15·t_k·b_j.

Прямое интегральное вейвлет-преобразование отраженного сигнала от сферы u_СФ(k) выполняется по аналогии с преобразованием Фурье, но в качестве базы используется не синусоидальный сигнал, а вейвлет ψ (a, b, k):

где u_СФ(k) - исследуемый сигнал с выхода регистрирующего индикаторного устройства (стробоскопического осциллографа);

ψ(a, b, k) - вейвлет Морле.

Так как форма базисных функций ψ(a, b, k) зафиксирована, то вся информация об исследуемом сигнале u_СФ(k) переносится на значения вейвлет-коэффициентов с(а, b). Энергетический вейвлет-спектр коэффициентов вычисляется по формуле

и является двумерным массивом амплитуд - значений вейвлет-коэффициентов

|c(a, b)|². Распределение этих значений в пространстве (а, b) дает информацию об изменении относительного вклада вейвлетных компонент разного масштаба «а» по параметру сдвига «b» (фиг.5, 6). Из рассмотрения фиг.6 можно легко определить координаты «блестящих точек». Координаты первой «блестящей точки» j=1:a_1max=64, b₁=140; координаты второй «блестящей точки» j=2: а_2max=150, b₂=235. Локальный энергетический частотный спектр каждой «блестящей точки» (7) для фиксированного значения b_j=t_j вейвлет-преобразования определяют при замене переменной временного масштаба «а» на переменную «f» (частоту) по формуле

где а_j - значение параметра масштаба для максимального значения энергетического спектра у-й «блестящей точки», соответствующей фиксированному значению b_j;

f_0j - частота максимального значения локального энергетического частотного спектра «блестящей точки» , определяемая с помощью коррелирующего вейвлета ψ(a, b, k) с найденными ранее параметрами w=3,7 и z=0,8 при значениях а_j, b_j.

Таким образом, формула для определения локального энергетического частотного спектра в сечении в_j имеет вид

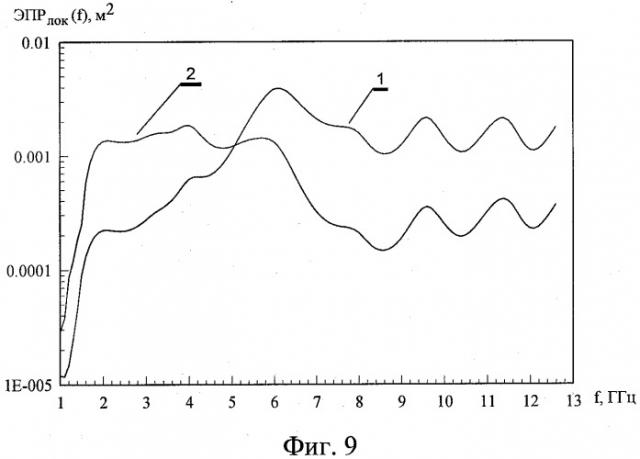
где c(f, b_j) - значения вейвлет-коэффициентов при фиксированном значении b_j. На фиг.7 приведены две временные зависимости энергетического вейвлет-спектра G_LСФ ²(t) отраженного сигнала от сферы, полученные из фиг.5, 6 при фиксированных значениях параметра масштаба а, т.е. на фиксированных частотах f_0j. График 1 фигуры 7 соответствует j=1 «блестящей точке» в момент времени t₁=0,171 нс зеркальной компоненты рассеяния с координатой a_1max=64 (частота f₀₁=7,692 ГГц), график 2, соответствует j=2 «блестящей точке» в момент времени t₂=0,287 нс дифракционной компоненты рассеяния с координатой а_2max=150 (частота f₀₂=3,226 ГГц). Необходимо отметить, что с понижением частоты, способствующем выделению дифракционной (ползущей) компоненте рассеяния, на графике 2 фиг.7 проявляется слабая, но хорошо заметная третья «блестящая точка» в момент времени t₃=1,562 нс, вызванная отражением ЭМ волны от обратной стороны сферы. Расстояние распространения ЭМ волны по образующей сферы L=πD/2=15·0.001221·t₃ строго соответствует временному отрезку пути до точки t₃, что свидетельствует о высокой разрешающей способности по дальности предложенного способа. Локальные энергетические частотные спектры G_LСФ ²(f) отраженного от сферы сигнала u_СФ(t) в сечениях t₁ и t₂ в полосе частот 1÷13 ГГц рассчитаны в соответствии с (7) и приведены на фиг.8. Локальные ЭПР_ЛОК (f) «блестящих точек» зеркальной (график 1) и дифракционной (график 2) компонент рассеяния сферы получены на основании (1) и приведены на фиг.9. Результаты фиг.9 находятся в соответствии с физической картиной процесса отражения. Действительно, если представить отклик отраженного от сферы сигнала как последовательность элементарных отсчетов дискретными отрезками времени t_j, причем, каждый из этих отрезков соответствует j-му поперечному сечению объекта, то эти сечения объекта можно представить как набор частотных фильтров, работающих на пропускание при отражении зондирующего сигнала со сверхширокой полосой. Наиболее прозрачные фильтры с их определяемой полосой пропускания (локальными частотными спектрами) идентифицируются как блестящие точки. Частотная характеристика каждого «фильтра» соответствует локальной ЭПР.

На чертежах изображено:

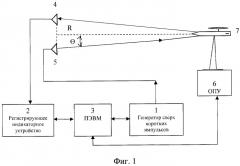
Фиг.1. Функциональная схема сверхширокополосного лабораторного радиолокационного измерительного комплекса (СШП ЛРИК).

Фиг.2. 1 - временная зависимость e_П(t) зондирующего сигнала в точке облучения объекта; 2 - временная зависимость аппроксимирующего комплексного вейвлета Морле e_В(t) с параметрами w=3,7 и z=0,8.

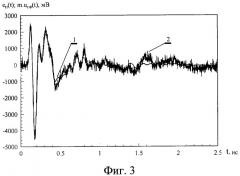
Фиг.3.1- временная зависимость e_П(t) зондирующего сигнала в точке облучения объекта; 2 - временная зависимость увеличенного в m раз отраженного от эталонной сферы сигнала u_СФ(t).

Фиг.4. Энергетический частотный спектр зондирующего поля G_П ²(f).

Фиг.5. Трехмерное изображение РР_ab энергетического вейвлет-спектра отраженного сигнала от сферы u_СФ(t).

Фиг.6. Плоское изображение РР_ab энергетического вейвлет-спектра отраженного сигнала от сферы u_СФ(t) с нанесением линий уровня амплитуды.

Фиг.7. Временные зависимости энергетического вейвлет-спектра G_LСФ ²(t) отраженного сигнала от сферы при значениях параметра масштаба: 1-a_1max=64 (частота f₀₁=7,692 ГГцУ); 2-а_2max=150 (частота f₀₂=3,226 ГГц); временные координаты блестящих точек: t₁=0,171 нс, t₂=0,287 нс.

Фиг.8. Локальные энергетические частотные спектры G_LСФ ²(f) отраженного от сферы сигнала u_СФ(t) в сечениях: 1-t₁=0,171 нс; 2-t₂=0,287 м.

Фиг.9. Локальные ЭПР_ЛОК (f) «блестящих точек» сферы: 1 - зеркальной компоненты рассеяния; 2 - дифракционной компоненты рассеяния.

Фиг.10. Трехмерное частотно-временное изображение энергетического вейвлет-спектра, отраженного от объекта радиолокационного наблюдения (модели летательного аппарата) сигнала при нулевом угле наблюдения (с носа).

Фиг.11. Плоское изображение энергетического вейвлет-спектра, отраженного от объекта сигнала при нулевом угле наблюдения.

Фиг.12. Трехмерное частотно-временное изображение энергетического вейвлет-спектра, отраженного от объекта сигнала при 180°-м угле наблюдениям (с хвоста).

Фиг.13. Плоское изображение энергетического вейвлет-спектра, отраженного от объекта сигнала при 180°-м угле наблюдения.

Фиг.14. Временная зависимость отраженного от объекта сигнала u(t) при 180°-ом угле наблюдения.

Фиг.15. Временные зависимости энергетического вейвлет-спектра G_Lj ²(t) отраженного сигнала u(t) от объекта при 180°-м угле наблюдения при значениях параметра масштаба: 1-а_1max=57 (частота f₀₁=8.393 ГГц), «блестящая точка» в момент времени t₁=0,549 нс; 2-а_2max=75 (частота f₀₂=6,333 ГГц), «блестящая точка» в момент времени t₂=0,977 нс; 3-a_3max=140 (частота f₀₂=3,448 ГГц), «блестящая точка» в момент времени t₃=1,163 нс.

Фиг.16. Локальные энергетические частотные спектры G_Lj ²(f) отраженного от объекта сигнала u (t) в сечениях t,=0,549 нс, t₂=0,977 нс и t₃=1,163 нс.

Фиг.17. 1, 2, 3 - локальные ЭПР_ЛОК (f) «блестящих точек» 1, 2, 3 в моменты времени: t₁=0,549 нс, t₂=0,977 нс, t₃=1,163 нс.

Заявленный способ измерения локальных ЭПР объектов может найти применение при исследовании сверхширокополосных локальных радиолокационных характеристик объектов при решении проблемы снижения их заметности, в том числе при выборе конструктивных особенностей формы объекта (пространственной конфигурации) в совокупности с применением современных радиопоглощающих покрытий. Использование СШП-сигналов, обладающих высоким разрешением по дальности в доли и единицы сантиметров, существенно расширяет возможности однопозиционной измерительной радиолокации. СШП-локация становится вполне равноправной альтернативой многопозиционным (радиоголографическим) методам решения задач снижения радиолокационной заметности объектов. Заявленный способ позволяет определить на поверхности исследуемого радиолокационного объекта локальные, наиболее интенсивные центры рассеяния, определяемые как те или иные конструктивные детали этого объекта, вносящие свой вклад в измеряемое поле рассеяния. Заявленный способ применим при исследовании уменьшенных и крупномасштабных моделей объектов на измерительных радиолокационных полигонах и может использоваться при отсутствии безэховых экранированных камер. Способ реализуется устройством, представляющим собой сверхширокополосный лабораторный радиолокационный измерительный комплекс (СШП ЛРИК), функциональная схема которого приведена на фиг.1. Устройство включает: 1 - генератор сверхкоротких импульсов TMG 050030 VP 11, 2 - регистрирующее устройство (стробоскопический осциллограф TMR 814), 3 - персональную электронную вычислительную машину (ПЭВМ), 4 - приемную антенну П6-23М, 5 - передающую антенну П6-23М, 6 - опорно-поворотное устройство (ОПУ), управляемое ПЭВМ, 7 - объект (модель летательного аппарата). R=3,3 м - расстояние от антенн до цели. Выход генератора сверхкоротких импульсов 1 соединен с входом передающей антенны 5, которая связана с исследуемым объектом 7 посредством излучаемого сигнала. Отраженный сигнал связывает исследуемый объект 7 с приемной антенной 4 посредством отраженного сигнала. Выход антенны 4 соединен с входом регистрирующего устройства 2. С помощью ПЭВМ 3 через интерфейс осуществляется управление ОПУ 6 и измерительными блоками 1 и 2 при использовании специального программного обеспечения. Устройство для измерения ЭПР объектов работает следующим образом.

Генератор сверхкоротких импульсов 1 формирует зондирующий сигнал в виде последовательности сверхкоротких импульсов, который через передающую антенну 5 излучается в направлении объекта. Отраженный сигнал через приемную антенну 4 поступает на вход регистрирующего устройства 2. С выхода регистрирующего устройства 2 измеренный сигнал поступает на ПЭВМ 3, где вычисляются значения локальных ЭПР центров отражения с использованием заранее веденным в память ЭВМ значением энергетического частотного спектра зондирующего поля G_П ²(f).

Исследуемый радиолокационный объект сложной формы в виде уменьшенной модели беспилотного летательного аппарата устанавливали на вертикальный пилон ОПУ так, чтобы его продольная ось фюзеляжа была параллельна горизонтальной оси. Рупоры антенн 4 и 5 располагались горизонтально на одинаковой высоте с объектом локации на расстоянии 0,38 м один от другого, поляризация излучения горизонтальная. Угол θ составил 3°.

Энергетические спектрограммы вейвлет-коэффициентов, изображенные на фиг.10-13, получены из обработки по формуле (4) в базисе того же аппроксимирующего зондирующее поле вейвлета с параметрами w=3,7 и z=0,8 отраженных от объекта сигналов u(t). Временная зависимость отраженного от объекта сигнала u(t) при 180°-м угле наблюдения показана на фиг.14. Из анализа изображений спектрограмм на фиг.10, 13 можно сделать вывод, о том, что при различных углах наблюдения спектрограммы вейвлет-коэффициентов отраженного от цели сигнала сильно отличаются не только количеством блестящих точек, но и интенсивностью их отражения. Уместно заметить, что при смене угла наблюдения (при смене ракурса объекта) на вейвлет-спектрограммах энергетического спектра отраженного сигнала «блестящие точки» изменяют свою интенсивность, формируя радиолокационное изображение объекта. На фиг.13 выбраны три наиболее интенсивные «блестящие точки» - 1, 2, 3. На фиг.15 приведены три временные зависимости энергетического вейвлет-спектра G_L ²(t) отраженного сигнала u(t) от объекта при 180°-м угле наблюдения. График 1, фиг.15 соответствует «блестящей точке» 1 в момент времени t₁=0,549 нс с координатой а_1max=57 (частота f₀₁=8.393 ГГц), график 2, соответствует «блестящей точке» 2 в момент времени t₂=0,977 нс с координатой а_2max=75 (частота f₀₂=6,393 ГГц), график 3 соответствует «блестящей точке» 3 в момент времени t₃=1,163 нс с координатой a_3max=140 (частота f₀₂=3,448 ГГц). Локальные энергетические частотные спектры G_Lj ²(f) отраженного от объекта сигнала u (t) в сечениях t₁, t₂ и t₃ для « блестящих точек» - 1, 2, 3 в полосе частот 1÷13 ГГц рассчитаны в соответствии с (7) и приведены на фиг.16. Локальные ЭПР (σ_Lj(f)) «блестящих точек» 1, 2, 3 компонент рассеяния отраженного от объекта сигнала получены на основании формулы (1) и приведены на графиках 1, 2, 3 фиг.17.

Таким образом, предложен новый способ, позволяющий за короткое время в сверхширокой полосе частот определить локальные ЭПР радиолокационных объектов с повышенной точностью за счет временной локализации спектральных компонент отраженного сигнала и предварительного определения локальных энергетических частотных спектров центров рассеяния.

Способ измерения локальных эффективных поверхностей рассеяния (ЭПР) радиолокационных объектов, основанный на облучении объекта сигналом, приеме отраженного от этого объекта сигнала и вычислении локальных ЭПР, отличающийся тем, что радиолокационный объект облучают последовательностью сверхкоротких импульсов, измеряют временную зависимость зондирующего сигнала в точке облучения объекта на расстоянии R от антенн, аппроксимируют эту зависимость вейвлетом Морле и находят численные значения его параметров w и z, используя преобразование Фурье временной зависимости зондирующего сигнала определяют энергетический частотный спектр зондирующего поля G_П ²(f), далее регистрируют временной сигнал, отраженный от объекта, в базисе найденного аппроксимирующего вейвлета вычисляют энергетический вейвлет-спектр коэффициентов вейвлет-преобразования отраженного сигнала, на вейвлет-спектрограмме энергетического спектра в координатах параметров масштаба и сдвига определяют значения параметров масштаба и сдвига, соответствующих максимуму отраженной энергии, обусловленному исследуемым локальным центром рассеяния - «блестящей точкой», для сечения энергетического вейвлет-спектра отраженного сигнала исследуемой «блестящей точки» вычисляют локальный энергетический спектр коэффициентов вейвлет-преобразования, определяют среднюю частоту вейвлета с параметрами w, z и параметрами масштаба и сдвига на вейвлет-спектрограмме исследуемой «блестящей точки», определяют диапазон частот исследуемого локального энергетического частотного спектра, определяют локальный энергетический частотный спектр «блестящей точки» , по формуле определяют локальную ЭПР σL_j(f) исследуемого локального центра рассеяния объекта.