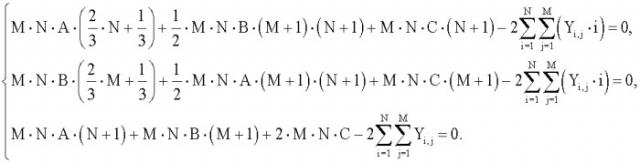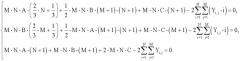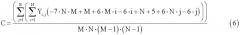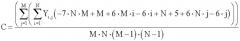Двумерный способ наименьших квадратов и устройство для его реализации

Двумерный способ наименьших квадратов и устройство для его реализации

Иллюстрации

Показать все

Реферат

Предлагаемое изобретение относится к информационно-измерительным устройствам и может быть использовано в вычислительной технике, в системах управления и обработки сигналов.

В общем случае, упрощенная математическая модель результатов измерений представляет собой двумерную дискретную последовательность

Y_i,j, вида:

где S_i,j - низкочастотная, медленно меняющаяся полезная составляющая;

η_i,j - аддитивная шумовая составляющая, распределенная по гауссовскому закону с нулевым математическим ожиданием и постоянной дисперсией;

N - количество строк, М - количество столбцов двумерного массива результатов измерений.

Основная решаемая задача - получение двумерной оценки полезной составляющей.

Подобная задача может возникнуть: 1) в работе приемо-передающих устройств дальней или космической связи; 2) в радиотехнике при обработке сигналов; 3) в системах цифровой обработки изображений; 4) в метеорологии и экономике при обработке результатов измерений.

Известен способ аппроксимаций функций по минимаксному критерию [Гольденберг Л.М. Цифровая обработка сигналов: Справочник / Л.М.Гольденберг, Б.Д.Матюшкин, М.Н.Поляк. - М.: Радио и связь, 1985. - 312 с., ил.]. Этот способ позволяет для одномерной реализации результатов измерений Y₁, Y₂, …, Y_N исходного процесса найти оценку минимизируящая функция вида:

На практике, при решении минимаксных задач аппроксимации более целесообразно использовать класс алгоритмов Ремеза и Вале-Пуссена. В этих алгоритмах используются множества точек, удовлетворяющих условиям Чебышевского альтернанса. Для поиска точек Чебышевского альтернанса при решении задач полиноминальной аппроксимации используются численные процедуры, имеющие итерационный характер.

Признаки способа-аналога, совпадающие с признаками заявляемого технического решения, следующие: запоминание дискретного сигнала, решение задачи аппроксимации, замена исходной дискретной реализации результатов измерений сглаженными значениями.

Недостатками известного способа являются

- сложность решения задачи Чебышевского приближения;

- отсутствие точных методов определения точек Чебышевского альтеранса;

- скорость сходимости алгоритма чебышевской аппроксимации существенно зависит от эффективности алгоритма поиска приближения на каждой итерации;

- невозможность аппроксимации двумерных реализации результатов измерений.

Причины, препятствующие достижению требуемого технического результата, заключаются в следующем:

- функция минимаксного критерия не является дифференцируемой.

Известен способ экспоненциального сглаживания [Бендат Дж., Пирсол А. Прикладной анализ случайных данных. - М.: Мир, 1989. - 540 с]. Его особенность заключается в том, что в процедуре нахождения оценки полезной составляющей используются только предшествующие значения входной реализации результатов измерения, взятые с определенным «весом», причем значение «весов» убывает к началу реализации. Для применения этого способа достаточно одной реализации Y₁, Y₂, …, Y_N исходного процесса.

Способ экспоненциального сглаживания предполагает запоминание исходной дискретной реализации результатов измерений Y₁, Y₂, …, Y_N случайного процесса, выбор параметра сглаживания α, (0<α<1), начального значения оценки S₀, вычисление оценки полезной составляющей по рекуррентному выражению:

замену исходных значений результатов измерения Y₁, Y₂, …, Y_N сглаженными значениями

Для использования способа экспоненциального сглаживания результатов измерений определяется начальное значение S₀ оценки полезной составляющей и параметр сглаживания α.

Признаки устройства-аналога, совпадающие с признаками заявляемого технического решения, следующие: запоминание дискретного сигнала, представление значений оценки полезной составляющей в виде многочлена от значений исходной дискретной реализации результатов измерений, замена значений исходной реализации сглаженными значениями.

Недостатками известного устройства являются:

- неопределенность выбора параметра сглаживания α, в отдельных случаях предлагается (необоснованно) определять величину α исходя из объема сглаживаемой реализации α=2/(N+1);

- неопределенность выбора параметра S₀, что приводит к многократному применению способа экспоненциального сглаживания при других значениях α и S₀ для достижения необходимой эффективности сглаживания в смысле заданного критерия;

- невозможность аппроксимации двумерных реализации результатов измерений.

Причины, препятствующие достижению требуемого технического результата, заключаются в следующем: способ экспоненциального сглаживания не является «самонастраивающимся» способом, поскольку выбор параметров α и S₀ осуществляется субъективно и зависит от опыта и практических навыков исследователя, значения α и S₀ являются функциями формы сигнала, шума, объема выборки.

Структурная схема устройства, реализующего рассмотренный способ, содержит генератор таковых импульсов, коммутатор, блок управления, регистр хранения, сумматор, блок умножения, выходной регистр хранения оценки полезной составляющей.

Известен способ переменных разностей [М.Кендалл, А.Стьюарт, Многомерный статистический анализ и временные ряды. - М.: Наука, 1976. - 736 с]. Для использования данного способа достаточно одной реализации Y₁, Y₂, …, Y_N исходного процесса.

Если имеется полезная составляющая, описываемая полином (или локально представляемая полиномом) с наложенной на нее случайной составляющей (шумом), можно исключить полиномиальную часть вычислением последовательных разностей ряда. Разности полинома порядка m представляют собой полином порядка m-1. Далее, если ряд содержит полином порядка р, то переход к разностям, повторенный (р+1) раз, исключает его и оставляет элементы, связанные со случайной компонентой исходного ряда.

В общем случае получается:

ΔY_k=Y_k+1-Y_k,

Δ²Y_k=ΔY_t+1-ΔY_k=Y_k+2-Y_k+1-Y_k+1-Y_k=Y_k+2-2Y_k+1-Y_k,

где σ² - дисперсия случайной составляющей.

Из последнего соотношения получается

Следовательно, метод последовательных разностей переменной состоит в вычислении первых, вторых, третьих и т.д. разностей, определении сумм квадратов, делении на и т.д. и обнаружении момента, когда это отношение становится постоянным. Таким образом, определяется оценка порядка полинома, содержащегося в исходном ряде, и дисперсии случайной составляющей.

Признаки способа-аналога, совпадающие с признаками заявляемого технического решения, следующие: запоминание дискретного сигнала, решение задачи аппроксимации, замена исходной дискретной реализации результатов измерений сглаженными значениями.

Недостатками известного способа являются:

- невозможность аппроксимации двумерных реализации результатов измерений;

- данный метод не исключает таких систематических составляющих, как периодические колебания с малым периодом.

Причины, препятствующие достижению требуемого технического результата, заключаются в следующем:

- способ переменных разностей не исключает экспоненциальной или циклической составляющей.

Наиболее близким к изобретению является способ наименьших квадратов и устройство для кусочно-линейной аппроксимации [Бендат Дж., Пирсол А. Прикладной анализ случайных данных: Пер. с англ. - М.: Мир, 1989. - 540 с., авторское свидетельство №1624479].

Способ наименьших квадратов позволяет для результатов измерений Y₁, Y₂, …, Y_N исходного процесса получить оценку минимизируя целевую функцию вида:

В случае, когда представляет собой полином первой степени коэффициенты а и b можно найти, минимизируя целевую функцию вида

Дифференцируя выражение (2) по а и b и приравнивания к нулю, получаем систему линейных уравнений

Решением системы является:

При оценке сумма квадратов отклонений значений оценки от значений реализации измерений является минимальной (2).

Недостатками известного способа-аналога являются:

- при использовании данного способа необходима априорная информация о функции полезного сигнала;

- ошибка полезной составляющей имеет вдоль реализации, в общем случае, нелинейную зависимость и достигает своих максимальных значений на границах интервала аппроксимации;

- при неполиноминальной модели оценки полезной составляющей строгое решение задачи минимизации целевой функции способа наименьших квадратов не всегда существует в силу нелинейности решаемой системы уравнений;

- невозможность аппроксимации двумерных реализации результатов измерений.

Причины, препятствующие достижению требуемого технического результата, заключаются в следующем:

- эффективность оценки полезной составляющей зависит от объема реализации, статистических характеристик аддитивного шума и наличия априорной информации о функциональной зависимости модели полезной составляющей.

Структурная схема устройства для кусочно-линейной аппроксимации содержит группу последовательно соединенных регистров, первый и второй вычитатели, сумматор, первый и второй накапливающие сумматоры, элементы задержки, генератор тактовых импульсов, два умножителя и два делителя на постоянный коэффициент.

Предлагаемый двумерный способ наименьших квадратов и устройство для его реализации позволяют выделять полезную составляющую при наличии единственной двумерной дискретной реализации измеряемого процесса.

Исходные результаты измерений представляют собой дискретную последовательность значений измеряемой физической величины Y_i,j в соответствии с выражением (1).

Для двумерного массива результатов измерений Y_i,j осуществляются аппроксимации исходных значений плоскостью, описывающейся уравнением первой степени вида:

Для нахождения значений коэффициентов А, В и С минимизируется целевая функция вида:

Дифференцируя последнее выражение по А, В и С и приравнивания к нулю, получаем систему линейных уравнений:

Решением системы является

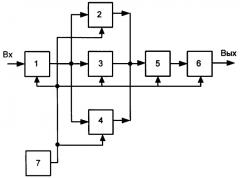
Устройство для реализации двумерного способа наименьших квадратов (фиг.1) содержит блок хранения входной реализации 1, вход которого является информационным входом устройства, выход блока хранения входной реализации 1 подключен к входу блока вычисления первого коэффициента 2, входу блока вычисления второго коэффициента 3 и входу блока вычисления третьего коэффициента 4, выход блока вычисления первого коэффициента 2, блока вычисления второго коэффициента 3 и блока вычисления третьего коэффициента 4 подключен к входу блока аппроксимации 5, выход которого подключен к входу блока хранения оценки полезной составляющей 6, выход которого является информационным выходом устройства, синхронность работы устройства задается тактовым генератором 7.

Устройство для реализации двумерного способа наименьших квадратов работает следующим образом.

Исходная входная двумерная реализация результатов измерений записывается в блок хранения входной реализации 1. В блоках вычисления первого коэффициента 2, вычисления второго коэффициента 3 и вычисления третьего коэффициента 4 вычисляются коэффициенты А в соответствии с выражением (4), В (5), С (6) соответственно, используя значения с блока хранения входной реализации. В блоке аппроксимации 5 производится оценка полезной составляющей в соответствии с выражением (3). Оценка полезной составляющей передается с выхода блока аппроксимации 5 на вход блока хранения оценки полезной составляющей 6.

Двумерный способ наименьших квадратов реализуется следующим образом.

На основе значений входной реализации результатов измерений вычисляются коэффициенты А, В и С в соответствии с выражением (4), (5) и (6) соответственно. Далее для двумерного массива результатов измерений осуществляется аппроксимация исходных значений плоскостью, описывающейся уравнением первой степени вида (3).

Технический результат - выделение двумерной оценки полезной составляющей при наличии единственной дискретной реализации измеряемого процесса.

Устройство для выделения двумерной оценки полезной составляющей при наличии единственной дискретной реализации измеряемого процесса, содержащее блок хранения результатов измерения, представленных в видеYi,j=Si,j+ηi,j, где i=1,N, j=1, M,Yi,j - результаты измерения;Si,j -низкочастотная медленно меняющаяся полезная составляющая;ηi,j - аддитивная шумовая составляющая по гауссовскому закону с нулевым математическим ожиданием и постоянной дисперсией;N - количество строк;М - количество столбцов двумерного массива результатов измерения,вход которого является информационным входом устройства,выход указанного блока хранения результатов измерения подключен к входу блока вычисления первого коэффициента в виде входу блока вычисления второго коэффициента в виде входу блока вычисления третьего коэффициента в виде выход блока вычисления первого коэффициента, блока вычисления второго коэффициента и блока вычисления третьего коэффициента подключен к входу блока аппроксимации для оценки полезной составляющей в видеSi,j=Ai+Bj+C, где i=1,N, j=1,M,выход которого подключен к входу блока хранения оценки полезной составляющей, выход которого является информационным выходом устройства, и тактовый генератор, предназначенный для обеспечения синхронизации работы устройства.