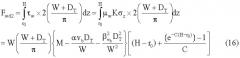Прогнозирование величины полости в системах уплотненного слоя с использованием новых корреляций и математической модели

Прогнозирование величины полости в системах уплотненного слоя с использованием новых корреляций и математической модели

Иллюстрации

Показать все

Реферат

Область техники, к которой относится изобретение

Настоящее изобретение относится к прогнозированию величины полости в системах уплотненного слоя частиц с использованием новых корреляций и математической модели. На основе аналитического решения одномерной математической модели разработаны упрощенные уравнения наряду с корреляциями полости, для того чтобы описать величину полости и гистерезис. Предложенные корреляции и математическая модель обеспечивают универсальный подход, чтобы прогнозировать величину полости, который можно использовать для любой системы уплотненного слоя частиц типа доменных печей, вагранки, процесса Corex, каталитического регенератора и др., и с помощью этого подхода можно успешно обработать данные других исследователей при условии, что известны фрикционные свойства твердых частиц. Разработанные корреляции и модели могут быть использованы непосредственно для оптимизации вышеуказанных и других родственных процессов.

Уровень техники

Уплотненный слой частиц. В уплотненном слое частиц при объяснении свойств слоя в различных условиях детально были рассмотрены контактные силы между частицами и стенкой-частицами. Можно сослаться на работу F.J.Doyle III, R.Jackson и J.C.Ginestra, "The phenomenon of pinning in an annular moving bed reactor with crossflow of gas", Chem. Eng Sci, 41(6) 1986 1485, в которой авторы теоретически исследовали движущийся слой поперечного потока, для того чтобы изучить эффект закрепления в реакторе каталитического риформинга. В основе этого анализа лежит подход баланса сил с учетом гидравлического сопротивления газа, напряжений и силы тяжести. Эта упрощенная модель, представленная в процитированной работе, имеет следующие недостатки: (i) она основана на произвольном предположении радиального изменения напряжения в движущемся слое. По этой причине расчетные значения по модели более чем в два раза превышают ограниченные экспериментальные значения; (ii) авторы предположили, что касательное напряжение при стенке в реакторе с движущимся слоем действуют в нисходящем направлении; (iii) анализ ограничен рассмотрением роста полости до прекращения потока твердого вещества в движущемся слое. Можно сослаться на работу V.B.Apte, T.F.Wall и J.S.Truelove: AIChEJ, 1990, том 36 (3), с.461-468, в которой авторы проанализировали распространение напряжения выше полости, образовавшейся за счет продувки газа снизу вверх от двумерно уплотненного слоя частиц. Авторы рассмотрели одномерный элементарный баланс сил между давлением, массой слоя и фрикционными силами наряду с направлением потока, совпадающим с осью фурмы. Эта модель имеет следующие недостатки: (i) предполагается, что фрикционные напряжения всегда направлены вверх; (ii) модель не способна описать какие-либо результаты гистерезиса; (iii) модель не учитывает какие-либо эффекты ускорения, вызванные замедлением потока газа; (iv) не может прогнозировать величину полости. Главным образом, это исследование направлено на распространение напряжений в уплотненном слое частиц при увеличении скорости. Можно сослаться на работу J.F.MacDonald, и J.Bridgewater, Chem. Eng. Sci, 1997, том 52 (5), с.677-691, в которой авторы исследовали явление образования пустот в неподвижном и движущемся слоях твердого вещества и унифицировали характеристики таких систем, используя анализ размерности. Недостатком этой корреляции является то, что несмотря на понимание значимости фрикционных сил в поперечном потоке они не включили эти силы в анализ размерности.

Доменная печь (производство чугуна, свинца, процесс Corex и др.). В доменной печи в уплотненный слой частиц кокса сбоку вводится с высокой скоростью газ, через трубопровод, названный фурмой. При этом создается полость спереди фурмы, названная подводящим каналом. В этой зоне кокс сгорает, обеспечивая тепло для процесса. Следовательно, в этой зоне частицы кокса расходуются, и они восполняются за счет поступления свежих частиц кокса сверху подводящего канала. Таким образом, вся пустая порода опускается в нисходящем направлении. Размер и форма подводящего канала влияют на аэродинамику печи и, таким образом, влияют на общий тепло- и массообмен. По этой причине подводящий канал был всесторонне изучен как теоретически, так и экспериментально. В случае доменной печи многие авторы разработали корреляции подводящего канала, чтобы прогнозировать размер подводящего канала, которые перечислены в таблице 1. Большинство этих корреляций основаны на исследовании “холодной” модели, и некоторые из них основаны на исследовании “горячей” модели и данных установки.

Можно сослаться на работы J.D.Lister, G.S.Gupta, V.R.Rudolph и Е.Т.White: СНЕМЕСА'91 Conf., 1991 Newcastle, Australia, том 1, 476 и S.Sarkar, G.S.Gupta, J.D.Litster, V.Rudolph, E.T.White и S.K.Choudhary: Metall Trans., 2003, 34B (2), 183-191, в которых отмечено, что ни одну из этих корреляций нельзя использовать для корректного прогнозирования размера подводящего канала в промышленных условиях, и, кроме того, они отличаются друг от друга. Отмечается, что все экспериментальные корреляции основаны на различных формах критерия Фруда. Согласно общепринятому подходу размер подводящего канала коррелирует с этим критерием наряду с некоторыми другими параметрами, такими как высота слоя, ширина модели и отверстие фурмы.

Можно сослаться на работы J.F.Elliott, R.A.Bachanan и J.B.Wagstaff: Trans. AIME, 1952, том 194, с.709-717. J.Taylor, G.Lonie и R.Hay: JISI, 1957, том 187, с.330; J.B.Wagstaff и W.H.Holman: Trans. AIME, March 1957, с.370-376. M; Hatano, В.Hiraoka, M.Fukuda и Т.Masuike: Int. ISU, 1977, 17, с.102-109; M.Nakamura, T.Sugiyama, Т.Uno, Y.Hara и S.Kondo: Tetsu-to-Hagane, 1977, том 63, с.28, из которых видно, что эти корреляции (см. таблицу I указанного документа) не развиваются на основе систематического исследования, то есть с применением анализа размерности и нахождения соответствующих групп.

С другой стороны, были получены теоретические корреляции путем последовательного упрощения фактически теоретических уравнений, в работе C.J.Flint и J.M.Burgess: Metall. Trans., 1992, том 23В, с.267-283, и J.Szekely и J.J.Poveromo: Metall. Trans., 1975, том 6В, с.119-130. Эти корреляции являются более систематическими. Кроме того, для двумерных и трехмерных моделей все эмпирические корреляции были получены в условиях возрастающей скорости. Здесь следует отметить, что при одном и том же значении скорости газа можно получить два значения размера подводящих каналов в зависимости от того, как проводятся измерения: при возрастании или убывании скорости газа. Это явление называется гистерезисом подводящего канала. Можно сослаться на работы J.D.Lister и др. 1991 и S.Sarkar и др. 2003, в которых явление гистерезиса было подробно описано и указано, что корреляция с убывающей скоростью в большей степени соответствует работе доменной печи.

Поскольку размер подводящего канала в случаях возрастания и убывания скорости изменяется приблизительно в четыре раза, размер подводящего канала может существенно влиять на прогнозирование процессов переноса тепла, массы и импульса в доменной печи. В сложившейся ситуации необходимо отметить кое-что о гистерезисе подводящего канала, поскольку предпосылки для корреляций/математической модели, разработанных в этой работе, основаны на этом явлении. Можно сослаться на работу S.Sarkar и др. 2003, в которой подробно истолковано явление гистерезиса подводящего канала и на основе собственных экспериментальных результатов предполагается, что гистерезис подводящего канала можно представить следующим уравнением:

Усилие давления - вес слоя ± фрикционные силы (напряжения) = 0 (1)

Физическая интерпретация этого уравнения состоит в том, что при расширении подводящего канала частицы вблизи и выше подводящего канала выталкиваются в восходящем направлении. Таким образом, фрикционные напряжения имеют тенденцию противодействовать этому движению частиц и поэтому действуют в нисходящем направлении и становятся полностью мобилизированными. Когда скорость продувки начинает снижаться от максимального значения, частицы выше подводящего канала пытаются упасть вниз. Следовательно, фрикционные силы противодействуют этому движению и постепенно начинают возрастать по величине в восходящем направлении. После того как фрикционные напряжения, действующие в восходящем направлении, становятся полностью мобилизированными, дальнейшее уменьшение скорости продувки приводит к уменьшению проницаемости подводящего канала. Положительный знак в уравнении (1) для члена фрикционных сил указывает на пристеночное трение полости, действующее вверх (при снижении скорости), а отрицательный знак указывает на пристеночное трение полости, действующее вниз (при увеличении скорости). Усилие давления всегда действует в восходящем направлении, а вес слоя всегда действует в нисходящем направлении.

Сущность изобретения

Основной целью настоящего изобретения является создание способа и системы для прогнозирования величины полости в уплотненном слое частиц, с использованием новых корреляций и/или математической модели, которые лишены указанных выше недостатков.

Соответственно настоящее изобретение направлено на создание способа и системы для прогнозирования величины полости в уплотненном слое частиц с использованием новых корреляций и/или математической модели, которые включают в себя разработку двух корреляций, по одной соответственно для возрастающей и убывающей скорости газа, на основе π-теоремы для экспериментов в рамках двумерной холодной модели, включающей такие переменные, как высота слоя, отверстие фурмы, доля пустот, фрикционные и физические свойства различных материалов, скорость газового потока и ширина модели, а также включают в себя разработку одномерной математической модели на основе подхода баланса сил (который рассмотрен в уровне техники) и последующее аналитическое решение разработанных уравнений относительно усилия давления, фрикционных сил и массы слоя, с целью описания гистерезиса полости и прогнозирования размера полости/подводящего канала и определения минимальной скорости фонтанирования/нестабильности в уплотненном слое частиц с последующим сопоставлением результатов корреляций и модели с экспериментальными и опубликованными заводскими данными о величине полости.

В варианте воплощения настоящее изобретение разъясняет и дает логическое объяснение направлению фрикционных сил, для того чтобы описать гистерезис в уплотненном слое частиц. В другом варианте воплощения настоящего изобретения также обнаружено, что данные при убывающей скорости относятся к работе доменных печей.

В еще одном варианте воплощения настоящего изобретения с использованием математической модели, определяется максимальная рабочая скорость газа в уплотненном слое частиц, при превышении которой слой становится нестабильным.

Краткое описание прилагаемых чертежей

В чертежах, прилагаемых к настоящему изобретению:

Фигура 1 иллюстрирует экспериментальный гистерезис полости в уплотненном слое частиц.

Фигура 2 иллюстрирует уплотненный слой частиц с демонстрацией существенных областей, использованных для моделирования.

Фигура 3 иллюстрирует силы, действующие на элемент в декартовской области.

Фигура 4 иллюстрирует силы, действующие на элемент в радиальной области.

Фигура 5 иллюстрирует принципиальную схему экспериментальной установки.

Фигура 6 иллюстрирует кривую гистерезиса нормального напряжения при скорости, равной 40 м/с.

Фигура 7 иллюстрирует изменение градиента давления с расстоянием от поверхности слоя.

Фигура 8 иллюстрирует сопоставление статического давления с экспериментальными данными.

Фигура 9 иллюстрирует сопоставление теоретического и экспериментального размера полости при возрастающей скорости.

Фигура 10 иллюстрирует сопоставление теоретического и экспериментального гистерезиса полости.

Фигура 11 иллюстрирует сопоставление теоретического размера полости с учетом фрикционных сил и без учета фрикционных сил.

Фигура 12 иллюстрирует сопоставление корреляции подводящего канала с данными для полистирольных частиц (3 мм), опубликованными Flint и Burgess (1992).

Фигура 13 иллюстрирует сопоставление корреляции подводящего канала с данными для частиц из стекла баллотини (0,725 мм), опубликованными Flint и Burgess(1992).

Фигура 14 иллюстрирует сопоставление прогнозирования по модели с экспериментальными значениями размера полости (Born, 1991).

Фигура 15 иллюстрирует сопоставление экспериментальных (Sastry, 2000) и теоретических значений размера полости.

Фигура 16 иллюстрирует сопоставление размера подводящего канала, найденного экспериментально и по корреляции при возрастающей, а также убывающей скорости.

Фигура 17 иллюстрирует сопоставление данных для доменной печи (Hatano и др., 1977) и эксперимента в условиях возрастающей, а также убывающей скорости.

Фигура 18 иллюстрирует сопоставление корреляции размера подводящего канала с опубликованными данными для доменной печи (Wgastaff, 1957).

Фигура 19 иллюстрирует сопоставление корреляции размера подводящего канала с опубликованными данными для доменной печи Nishi и др., 1982.

Фигура 20 иллюстрирует сопоставление корреляции размера подводящего канала с опубликованными данными для доменной печи Poveromo и др., 1975.

Фигура 21 иллюстрирует блок-схему для определения размера полости/подводящего канала в уплотненном слое частиц, таких как в доменных печах производства чугуна и свинца, corex, вагранках, и др. для убывающей скорости газа на основе математической модели.

Фигура 22 иллюстрирует блок-схему для определения размера полости/подводящего канала в уплотненном слое частиц, таких как в доменных печах производства чугуна и свинца, corex, вагранках, и др. для убывающей скорости газа на основе убывающей корреляции.

Фигура 23 иллюстрирует блок-схему для определения (на основе математической модели) максимальной скорости/размера полости в фонтанирующем слое, выше которой может образоваться выпускное отверстие или условия в уплотненном слое частиц станут нестабильными.

Фигура 24 иллюстрирует блок-схему для определения размера полости/подводящего канала в уплотненном слое частиц, таких как в доменных печах производства чугуна и свинца, corex, вагранках, и др.

Подробное описание изобретения

Соответственно настоящее изобретение обеспечивает компьютеризированный способ определения величины полости в системах уплотненного слоя частиц с помощью корреляции или математической модели, причем указанный способ включает в себя стадии:

(a) получение данных, относящихся к свойствам материала системы уплотненного слоя частиц;

(b) вычисление радиуса полости при возрастающей скорости газа, а также при убывающей скорости газа, используя математическую модель, которая включает в себя напряжения/фрикционные силы, в виде:

и

соответственно; или вычисление радиуса полости при возрастающей скорости газа, а также при убывающей скорости газа, используя математические уравнения на основе корреляции, в виде:

соответственно, и

(с) вычисление величины полости по значению радиуса полости, полученному на стадии (b).

В варианте воплощения настоящего изобретения данные относительно свойств материала уплотненного слоя частиц включают в себя высоту слоя, отверстие фурмы, порозность слоя, коэффициент трения стенки с частицами, коэффициент трения между частицами, скорость газа, ширину модели и фактор формы частиц.

В другом варианте воплощения настоящего изобретения данные относительно свойств материала уплотненного слоя частиц включают уже полученные экспериментальные данные или оперативные данные.

В еще одном варианте воплощения настоящего изобретения фрикционная сила (F_wd) в уравнениях 28 и 29 определяется выражением:

В еще одном варианте воплощения настоящего изобретения, в котором для определения радиуса полости используется корреляция с возрастающей скоростью, которая приведена в уравнении 33, с использованием π-теоремы разработаны важные безразмерные критерии

где использованы следующие символы: радиус доменной печи W, эффективная высота слоя Н, скорость продувки v_b, отверстие фурмы D_T, порозность слоя ε, вязкость газа µ_g, размер частиц d_p, фактор формы ϕ_s, плотность газа ρ_g, плотность твердого вещества ρ_s, коэффициент трения стенки µ_w, ускорение силы тяжести g, эффективный диаметр частиц определяется как d_eff=d_pϕ_s, эффективная плотность слоя определяется как ρ_eff=ερ_g+(1-ε)ρ_s, коэффициент трения частиц со стенкой определяется как µ_w=tanϕ_w, где ϕ_w представляет собой угол трения между стенкой и частицами, D_r означает диаметр полости, и все единицы выражены в системе SI.

В еще одном варианте воплощения настоящего изобретения, в котором для определения радиуса полости используется корреляция с убывающей скоростью, которая приведена в уравнении 36, с использованием π-теоремы разработаны важные безразмерные критерии

где использованы следующие символы: радиус доменной печи W, эффективная высота слоя Н, скорость продувки v_b, отверстие фурмы D_T, порозность слоя ε, вязкость газа µ_g, размер частиц d_p, фактор формы ϕ_s, плотность газа ρ_g, плотность твердого вещества ρ_s, коэффициент трения стенки µ_w, ускорение силы тяжести g, эффективный диаметр частиц определяется как d_eff=d_pϕ_s, эффективная плотность слоя определяется как ρ_eff=ερ_g+(1-ε)ρ_s, коэффициент трения частиц со стенкой определяется как µ_w=tanϕ_w, где ϕ_w представляет собой угол трения между стенкой и частицами, D_r означает диаметр полости, и все единицы выражены в системе SI.

В еще одном варианте воплощения настоящего изобретения системы уплотненных частиц включают доменные печи, вагранки, процесс Corex, каталитический регенератор.

В любом процессе, включающем газ и твердое вещество, важным фактором, определяющим показатели работы, является достижение равномерного распределения газа и твердого вещества. В эту категорию попадают уплотненный, фонтанирующий и кипящий слои, которые широко применяются в промышленности. Общим признаком всех этих слоев является то, что в них наблюдается гистерезис. На фигуре 1 приведен гистерезис полости в виде зависимости диаметра полости от скорости газа, которая наглядно демонстрирует наличие гистерезиса. Из этой фигуры видно, что величина полости возрастает с увеличением скорости газа. Когда скорость газа уменьшается от максимального значения (А), сначала величина полости почти не изменяется. Однако при достижении критической скорости (в точке В) величина полости начинает уменьшаться при снижении скорости, но полость остается всегда больше, чем на кривой с возрастанием скорости при одинаковом значении скорости. Это явление называется гистерезисом полости. Гистерезис полости, наблюдаемый в уплотненном слое частиц, подобен гистерезису, наблюдаемому в кипящем слое.

Здесь, на основе уравнения (1) представлена одномерная теоретическая модель для прогнозирования величины полости и для описания явления гистерезиса в уплотненном слое частиц. Кроме того, заявители представили новые корреляции размера полости/подводящего канала с использованием -π-теоремы. Ниже различные слагаемые в уравнении (1) выражены в математической форме.

Формулировка модели

Рассматривается двумерный уплотненный слой частиц твердого вещества высотой Н и шириной W, который продемонстрирован на фигуре 2. Газ вводится сбоку при специфической скорости продувки v_b через патрубок желобкового типа с диаметром отверстия D_T, создавая полость эквивалентного радиуса R перед патрубком. Пусть ρ и µ, означают плотность и вязкость газа соответственно, d_p представляет собой диаметр частиц и ε означает порозность слоя. D.Akamatsu, M.Hatano и М.Takeuchi, Tetsu-to-Hagane 58 (1972) 20 измерили давление внутри полости и обнаружили, что распределение давления является относительно равномерным. Следовательно, разумным является предположение, что газ радиально течет из центра полости в окружающий уплотненный слой частиц, причем скорость изменяется в соответствии с концентрическими кругами. На основе некоторых других данных экспериментального и теоретического исследования (Szekely и Poveromo (1975), Flint и Burgess (1992), V.B.Apte, T.F.Wall и J.S.Truelove, Gas Flows in Cavities Formed by High Velocity Jets in a Two-Dimensional Packed Bed, Chem. Eng. Res. Des. 66 (1988) 357, и М.Hatano, К.Kurita и Т.Tanaka, Ironmaking Proc. Iron Steel Soc. 42 (1983) 577) принято, что внутри полости имеются изобарические условия. Скорость газа в восходящем потоке изменяется в направлении радиуса r (расстояние от центра полости), но не изменяется в угловом направлении.

Давление, оказываемое газом. В работах (Flint и Burgess, 1992 и Apte et. al., 1990) сообщалось, что скорость газа становится почти равной скорости на выходе из слоя частиц на некотором расстоянии от центра полости, скажем r=r₀. Соответствующее значение скорости на этом расстоянии v=v_H (смотрите фиг.2). Затем, приравнивая массовую скорость потока газа из патрубка и на расстоянии r₀ от центра полости, можно получить

Кроме того, приравнивая массовую скорость потока продувки у патрубка и на поверхности слоя, можно получить

Из уравнений (2) и (3) можно получить

Начиная с расстояния r₀ от центра полости, скорость газа будет постоянной. Это наблюдение было подтверждено расчетом в работе Flint и Burgess, 1992. При анализе экспериментальных данных (Apte и др., 1990) также подтверждена справедливость уравнений (3) и (4).

Пусть скорость газа на расстоянии r от центра полости равна v(r). Тогда, приравнивая массовую скорость потока у отверстия патрубка и на расстоянии r от центра полости, получим

На основе приведенных выше уравнений моделированный профиль скорости может быть записан в виде:

v(r)=v_bD_T/(2πr-D_T), r<r₀ (6)

v(r)=v_H, r≥r₀

Следовательно, скорость восходящего потока газа изменяется обратно пропорционально расстоянию вплоть до расстояния от центра полости, равного r₀ (радиальная область), и затем остается постоянной за этим пределом (декартовская область).

Для тягового усилия в кипящем слое многие исследователи часто используют корреляцию Richardson-Zaki. Аналогично в уплотненном слое частиц сила, с которой газ воздействует на единицу объема твердого веществ, определяется из хорошо известного уравнения Ergun:

где и

ϕ_s представляет собой фактор формы частиц. На практике в радиальной области скорость газа является высокой. При таких высоких скоростях вкладом вязкостного слагаемого можно пренебречь по сравнению с инерционным слагаемым, то есть αv(r)<<βv²(r). Следовательно, сила, которую газ оказывает на твердые частицы, определяется как

или

Аналогично сила, которую газ оказывает в декартовской области, определяется как

и (W+D_T)/π=(2r₀) представляет собой диаметр наибольшей круга в области, где изменяется скорость, через которую газ проходит радиально и поступает в декартовскую область, как показано на фигуре 4. Величина z является переменной высотой уплотненного слоя частиц от уровня фурмы. После интегрирования уравнения (9) получаем

Следовательно, суммарная сила, которую оказывает газ (или при увеличении, или при уменьшении скорости) на частицы выше полости, можно определить как

F_pr-f=F₁+F₂

Определение фрикционной силы в декартовской области (приуменьшении скорости)

При уменьшении скорости фрикционная сила между частицами и стенкой действует в восходящем направлении, как объяснено ранее и показано на фигуре 3, наряду с другими силами, где ось z направлена вдоль восходящего направления от уровня фурмы или от центра полости. Предполагается, что нормальное напряжение (σ_z), действующее в восходящем направлении, является постоянным на любом расстоянии z от поверхности слоя, dz является толщиной слоя, в котором выполняется элементарный баланс. Пусть σ_z+dσ_z означает реактивное напряжение на расстоянии z+dz, действующее в нисходящем направлении, и τ_w - это фрикционное напряжение между частицей и стенкой. Масса слоя в единице объема равна М. Приравнивая силы, действующие на элемент, получим:

Множитель 2 при втором слагаемом в правой части обусловлен действием напряжения τ_w на обе стороны стенки. Сила воздействия газа на единицу поверхности всего элемента dP=(-∂p/∂z)dz. Используя подход Janssen (H.A.Janssen, Versuche uber getreidedruck in solozellen. Ver. Deutsch. Ing. Zeit. 39 (1895) 1045), принимаем, что основными видами напряжения являются вертикальное (σ_z) и горизонтальное напряжение (σ_х). Следовательно, фрикционное напряжение между частицами и стенкой можно записать в виде τ_w=µ_wKσ_z, где К=((1-sinϕ)/(1+sinϕ)) является коэффициентом бокового давления, ϕ - это угол внутреннего трения и µ_w представляет собой коэффициент трения между стенкой в слое и частицами. Подставляя значение τ_w в уравнение (11), после некоторого упрощения получим

Решением уравнения (12) с использованием граничного условия при z=Н, σ_z=0, будет:

где С=2µ_wK/W, представляет собой фактор поддержки слоя. Первое слагаемое в правой части уравнения (13) представляет собой эффективную массу слоя, в то время как второе слагаемое означает гидродинамическое сопротивление восходящего потока газа. Для равномерного потока газа в слое, то есть при постоянном градиенте -∂p/∂z, уравнение (13), после подстановки значения v_H из уравнения (3), сводится к

В случае отсутствия потока газа, то есть в неподвижном слое, уравнение (14) упрощается до

Это представляет собой классическое уравнение Jansen, при условии что напряжение σ_z является постоянным в любом горизонтальном сечении. Для глубоких слоев, когда (H-z)→∞, приведенное выше уравнение принимает вид σ_z=М/С.

Коэффициент С зависит от W, µ_w и К и поэтому является мерой фрикционной поддержки частиц стенкой. Предполагается, что чем больше значение С, тем больше фрикционная поддержка частиц стенкой, и поэтому уменьшается эффективная масса слоя. Кроме того, коэффициент С обратно пропорционален ширине модели: чем больше ширина модели, тем меньше коэффициент С. Из уравнения (15), когда предел lim_C→0 σ_z=M·(H-z), предполагая, что С=0, масса слоя может быть передана как эквивалентная гидростатическая высота столба.

Необходимо определить фрикционную силу между частицами и стенкой, действующую во всей этой области в декартовской системе. Фрикционная сила F_wd2 между частицами и стенкой, действующая в восходящем направлении в области, лежащей на расстоянии 2r₀, в области постоянной скорости определяется путем интегрирования в диапазоне от z=r₀ до z=H произведения фрикционного напряжения между частицами и стенкой, τ_w, на площадь.

Фрикционные силы в радиальной области. Аналогично декартовской области радиальная система для элементарного баланса показана на фигуре 4. Разрешая все силы вдоль радиального направления и соблюдая баланс сил для всей верхней части дугового элемента, получим

где dr представляет собой толщину дугового сегмента, в котором выполняется элементарный баланс, σ_r означает радиальное напряжение на радиусе r и σ_r+dσ_r - это реактивное напряжение на радиусе r+dr. Величина τ_w представляет собой фрикционное напряжение между частицами и стенкой, действующее в восходящем направлении, n - это фактор, учитывающий вклад верхней части полости в общую площадь полости, и h - это множитель, возникающий в результате разрешения вертикальной силы вдоль радиального направления. Таким образом,

и

Тогда, предполагая, что основными напряжениями являются σ_r и σ_θ, получим

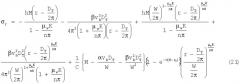
Подставляя значения τ_w и dP в уравнение (17), получим после интегрирования

Вблизи области полости, где скорость является весьма высокой, второе слагаемое в приведенном выше уравнении становится существенно большим, что приводит к снижению напряжения. Постоянная интегрирования А может быть рассчитана с использованием граничного условия на поверхности, разделяющей радиальную и декартовскую системы, то есть при r=r₀, σ_r=σ_z. Окончательно уравнение (20) можно записать в виде:

При добавлении слагаемых, содержащих массу слоя (М), в приведенное выше уравнение получают эффективную массу слоя, а при добавлении слагаемых, содержащих скорость продувки (v_b), получают эффективное гидродинамическое сопротивление восходящего потока газа. Фрикционную силу при стенке можно получить путем интегрирования от r=R до r=r₀ произведения величины τ_w, разрешенной по вертикальному направлению, на площадь, как показано ниже.

где р=h - коэффициент, полученный путем разрешения радиальной силы вдоль вертикально восходящего направления. После интегрирования уравнение (22) может быть записано в виде

Элементарный баланс сил при увеличении скорости

Этот баланс может быть выполнен таким же образом, как и в случае снижения скорости, см. диссертацию S.Rajneesh, M.E. (Int.) Thesis, Indian Institute of Science, Bangalore, Сентябрь. 2000 и отчет CSIR Report No. 22(285)/99/EMR-II.

Баланс сил вверху полости (для убывающей скорости)

Из уравнения (8) сила, оказываемая газом выше верхней части полости в области изменения скорости в вертикально восходящем направлении, (после разрешения) определяется как

Следовательно, общая сила, оказываемая газом на твердые частицы в восходящем направлении, равна

Аналогично, общая фрикционная сила между частицами и стенкой, действующая в восходящем направлении, равна

где силы F_wtd1 и F_wd2 определяются из уравнений (23) и (16) соответственно.

Предполагается, что масса слоя передается гидростатически над сводом полости. Для простоты предполагается, что вклад массы слоя с боков в образование полости является незначительным. Следовательно, масса слоя сверху свода полости равна:

где "n" - фактор вклада верхней части полости в площадь полости.

После подстановки всех сил (уравнения 25, 26 и 27) в уравнение (1) и некоторого упрощения можно записать уравнение в функции радиуса полости R.

При численном решении уравнения (28) относительно R получают радиус полости для случая уменьшения скорости и, таким образом, диаметр полости D_r=2R.

Аналогично можно рассмотреть баланс сил поверх полости в случае возрастающей скорости и можно определить диаметр полости, как показано выше.

Корреляции размера подводящего канала/полости

Случай увеличения скорости (с использованием π-теоремы BUCKINGHAM)

Подводящий канал образуется благодаря балансу между силой, оказываемой давлением газа, весом слоя и фрикционными силами, как описано в уравнении баланса сил (1). Сила, оказываемая давлением газа, включает в себя инерционную и вязкостную составляющую. Инерционная сила, оказываемая газом, зависит от скорости продувки (v_b, м/с), плотности газа (ρ_g, кг/м³) и отверстия фурмы (D_T, м). Сила, оказываемая вязкостным течением газа, зависит от вязкости (µ, Па·с) газа и диаметра частиц (d_p, м³). Вес уплотненного слоя зависит от плотности твердого вещества (ρ_s, кг/м), ускорения силы тяжести (g, м/с²), высоты слоя (Н, м) и порозности слоя. Фрикционные силы (или напряжения) зависят от внутреннего угла трения и угла стенки, что приводит к появлению коэффициента трения стенки с частицами, µ_w и коэффициента трения между частицами, ν. Окончательно учитывается ширина слоя W, поскольку она изменяется в ходе эксперимента, так как она влияет на проницаемость подводящего канала.

Другими словами, диаметр подводящего канала (D_r, м) в уплотненном слое частиц является функцией свойств материала, используемого в уплотненном слое, свойств газа, вводимого через фурму, геометрических параметров и фрикционных параметров, т.е.

Эффективный диаметр частиц определяется как d_eff=dp sh, где d_p - это диаметр частиц и sh означает фактор формы частиц. Эффективная плотность слоя определяется

как ρ_eff=sρ_g+(1-ε)ρ_s. Коэффициент трения стенки с частицами определяется как µ_w=tanϕ_w, и коэффициент трения между частицами определяется как ν=tanϕ, где ϕ и ϕ_w означают внутренний угол трения между частицами и угол трения между стенкой и частицами соответственно.

Поскольку общее число переменных равно 12 и число независимых переменных, исходя из которых могут быть выражены переменные, равно трем, число безразмерных групп, которые могут быть получены из π-теоремы Buckingham, равно 9. С использованием π-теоремы была получена корреляция для диаметра подводящего канала в виде:

Группа, включающая d_p и D_r, опущена, так как эти параметры уже представлены в некоторых других группах. Аналогично пренебрегают величиной ν, поскольку в двумерной холодной модели основной вклад дает трение между стенкой и частицами, а не трение между частицами. Кроме того, величина ϕ изменяется со скоростью газового потока (R. Jackson и M.R. Judd, Further consideration on the effect of aeration on the flowability of powders, Trans. Ichem. E, 59 (1981) 119), что затрудняет определение единственного значения ϕ.

Первая безразмерная группа в правой части относится к перепаду давления. Вторая группа представляет собой критерий Фруда, который дает отношение инерционных сил к гравитационным. Он используется для описания систем газ/твердое вещество/жидкость. Многие авторы предшествующих работ коррелировали размер подводящего канала с этим критерием. Третья группа является хорошо известным критерием Рейнольдса. Остальные сомножители в правой части уравнения (30) известны как фактор проницаемости подводящего канала.

Из экспериментальных данных, полученных в случае увеличения скорости, оценивают величины безразмерных групп. Затем полученные данные подвергают регрессионному анализу, чтобы определить постоянные а, b, с, d, e, f и k. Получены следующие значения этих постоянных: а=0,79, b=0,81, с=0,0035, d=0,88, е=0,89, f=-0,24 и k=243,5. Из этих значений ясно, что критерий Рейнольдса дает наименьший вклад. Все другие параметры являются значимыми. Поэтому после пренебрежения членом с критерием Рейнольдса и проведения повторного регрессионного анализа получены следующие значения коэффициентов: а=0,79, b=0,81, d=0,85, е=0,88, f=-0,23 и k=247. Можно