Способ автоматизированной оценки в полете суммарной тяги двигателей летательного аппарата

Способ автоматизированной оценки в полете суммарной тяги двигателей летательного аппарата

Иллюстрации

Показать все

Реферат

Область техники

Изобретение относится к технической физике, а именно к способам и устройствам для измерения суммарной тяги двигателей летательных аппаратов на основе измерений параметров в полете, сбора информации, ее обработки с помощью электронно-вычислительных машин (ЭВМ) без введения специальных систем или доработок штатных систем.

Уровень техники

Известен способ измерения тяги в полете гиперзвукового прямоточного воздушно-реактивного двигателя (ГПВРД) непилотируемой гиперзвуковой летающей лаборатории (ГЛЛ), патент US №2242736 от 20 декабря 2004 г.

В данном способе тяга двигателя определяется по приращению продольного ускорения (вдоль оси оX), создаваемого за счет действия силы тяги в полете. Для определения тяги двигателя производится разделение сил аэродинамического сопротивления вдоль продольной оси ГЛЛ, земного тяготения и тяги двигателя. С этой целью производится выключение и включение подачи топлива в камеру сгорания в короткие рядом стоящие промежутки времени t₁ и t₂, которые не превышают 1 сек. Силу тяги двигателя определяют по формуле:

R_ДВ=m_лл·ω_R,

где m_лл - масса ГЛЛ,

ω_R - ускорение ГЛЛ при действии силы тяги.

Ускорение ГЛЛ вычисляют по формуле:

ω_R=(n_xt1-n_xt2)·g,

где n_xt1 и n_xt2 - значения продольных перегрузок в моменты времени t₁ и t₂.

Недостатком этого способа является то, что при выключении и включении двигателя нарушается стационарный режим работы двигателя и полета ГЛЛ, в показаниях акселерометра присутствует составляющая перегрузки от силы лобового сопротивления, которая может быть достаточно велика при больших скоростных напорах. Это приводит к необходимости выбирать акселерометр с большим диапазоном измерений, что приведет к дополнительной динамической погрешности, в особенности при определении малой силы тяги. Кроме того, в случае летных испытаний ГЛЛ с большим аэродинамическим качеством выключение и включение двигателя приведет к дополнительным колебаниям ГЛЛ в продольной плоскости (по углу атаки). По показаниям одного такого акселерометра нельзя судить, по какой причине произошло изменение перегрузки: или колебаний угла атаки, или изменений силы тяги двигателя. При повторном выключении-включении двигателя задний фронт предыдущего импульса, т.е. импульса последействия, может быть достаточно продолжительным, что внесет дополнительную погрешность в величину определяемой силы тяги, т.к. импульс тяги и, соответственно, импульс перегрузки при повторном включении будет отсчитываться от остаточного уровня предыдущего импульса, что снижает точность измерений силы тяги в полете гиперзвукового прямоточного воздушно-реактивного двигателя гиперзвуковой летающей лаборатории, в особенности ГЛЛ с большим аэродинамическим качеством.

Известен способ определения тяги сопла газотурбинного двигателя в полете и устройство для его осуществления (патент РФ 223 0302, G011 5/13 от 2004.06.10), включающий измерение усилий сопротивления двумя прямолинейными зондами с различными коэффициентами аэродинамического сопротивления, размещенными в газовом потоке сопла, определение параметра, характеризующего отношение измеренных двумя зондами усилий, и определение скоростного напора газового потока с использованием предварительно полученных зависимостей параметра от числа М или разницы коэффициентов аэродинамического сопротивления зондов с последующим определением тяги. Измерение усилия сопротивления производят в полете на зондах, отклоненных от перпендикуляра к направлению потока на заданный угол α, определяют параметры, коэффициенты сопротивления зондов и скоростной напор по зависимостям, полученным на земле с зондами, размещенными перпендикулярно направлению газового потока, а тягу определяют по полученному значению скоростного напора, увеличенному в 1/cos²α раз. Кроме того, в устройстве содержатся размещенные в области среза сопла измерительные прямолинейные стержни из жаростойких сплавов, жестко закрепленных одним концом на конструкции сопла с помощью кронштейна и несущие силоизмерительные устройства, связанные выходами с блоком определения тяги. Стержни выполнены переставляемыми в узлах крепления к кронштейнам для обеспечения их поворота в вертикальной плоскости на заданный угол, а блок определения тяги снабжен задатчиком углов установки зондов. Кроме того, устройство снабжено датчиком измерения избыточного статического давления газового потока сопла, приемник статического давления установлен в области измерительных зондов. Устройство содержит блок питания и индикации. Управление устройствами осуществляют с помощью ЭВМ.

Однако недостатком данного способа является необходимость размещения на летательном аппарате (ЛА) дополнительного оборудования, сложной тарировки. Математическое и алгоритмическое обеспечение обработки результатов испытаний отличается большой трудоемкостью выполнения.

Наиболее близким техническим решением, принятым за прототип, является "Метод измерения тяги реактивного двигателя в реальном масштабе времени", патент EP №0342970. А2 от 19 мая 1988 г. В данном методе полная тяга двигателя определяется как разность общей силы, включающей подъемную силу самолета и силу аэродинамического сопротивления с учетом углов атаки и скольжения. Для определения этих составляющих в алгоритме расчетов используется большое количество измеряемых параметров, в том числе и перегрузок, измеряемых с помощью акселерометров.

Существенным недостатком данного метода является большая погрешность, которая обусловлена измерением в полете большого количества параметров, в том числе термодинамических параметров смеси газа: температур, показателей изоэнтропы (адиабаты) (k), газовой постоянной (R), с учетом реального состава газа.

Технической задачей предлагаемого способа является повышение достоверности оценки измерений суммарной тяги двигателей летательного аппарата во время полета.

Технический результат достигается за счет измерения в полете вектора состояния ЛА, использования уравнения движения ЛА в продольной плоскости, инвариантных линейных преобразований измерений для обеспечения условий несмещенности, минимальной дисперсии ошибки, условного экстремума путем введения функции Лагранжа при определении суммарной тяги двигателей по осям X, Y на выделенном небольшом скользящем базовом интервале, содержащем (2l+1) измерений каждого из рассматриваемых параметров, в равноотстоящие моменты времени Δt, на неустановившихся режимах полета для каждого скользящего интервала.

Как известно, в полете на ЛА действуют одновременно силы аэродинамического сопротивления, земного тяготения и тяга двигателей. Для определения тяги двигателей необходимо разделение этих сил.

Для достижения указанного технического результата в способе автоматизированной оценки в полете суммарной тяги двигателей ЛА, проводят комплексные измерения параметров самолетными датчиками продольной и нормальной перегрузки в центре масс, скоростного напора q_изм(t)=pV² _изм/2, скорости полета ЛА V_изм и плотность воздуха ρ в дискретные равноотстоящие моменты времени Δt. При этом проводят измерения на неустановившихся режимах полета, например, разгон, торможение, в которых скоростной напор воздушного потока изменяется быстро по отношению к исходному в балансировочном режиме. В качестве исходного балансировочного полета принимают горизонтальный полет на заданной высоте, определяют оценку суммарной тяги, используя аэродинамические соотношения вектора состояния летательного аппарата, уравнение движения ЛА в продольной плоскости, по осям координат X, Y с помощью БЦВМ, для этого обеспечивают автоматизированный цифровой анализ путем последовательного считывания каждой кривой измерений с небольшого скользящего базового интервала (СБИ), включающего (2l+1) измерений, каждого из рассматриваемых параметров, определяют значения проекций вектора тяги по осям координат X, Y в виде:

причем для определения указанных значений Р_x(t) и Р_y(t) вводят при обработке измерений скользящий базовый интервал (СБИ), содержащий (2·l+1) (обычно l≤5), измерений каждого из рассматриваемых параметров такого, что

где , - коэффициенты сил лобового сопротивления и подъемной силы в скоростной системе координат, α - угол атаки,

m - масса ЛА, g - ускорение силы тяжести, S - площадь крыла,

С_x, C_y - коэффициенты аэродинамических сил лобового сопротивления и подъемной силы в связанных осях координат, ε_x, ε_y - случайные ошибки;

полученные изменения тяги двигателя на интервале [t_-j,t_j] представляют в виде:

где R_x(t), R_y(t) - остаточный член разложения тяги в ряд по степеням t, результаты измерений на СБИ для упрощения вычислений представляют в матричном виде:

где Т - операция транспонирования

в расчеты вводят вектор неизвестных коэффициентов в соответствии со способом инвариантной фильтрации, умножают данные выражения на вектор неизвестных коэффициентов накладывают на выбор элементов вектора β следующие условия:

- инвариантности Q^Tβ=0,

-несмещенности: где и - значения сил тяги двигателей в средней точке СБИ,

- минимума дисперсии ошибки

а оценку β определяют путем решения задачи на условный экстремум введением функции Лагранжа:

где λ₀…λ_k - множители Лагранжа,

определяют коэффициенты из условия минимума функции Лагранжа:

для снижения дисперсии принимают:

затем вычисляют оценку значений составляющих вектора тяги по осям X, Y в каждой точке СБИ:

определяют величину суммарной тяги двигателя:

и угол между вектором Р_∑ и продольной осью самолета:

где

λ₀…λ_k+1 - множители Лагранжа.

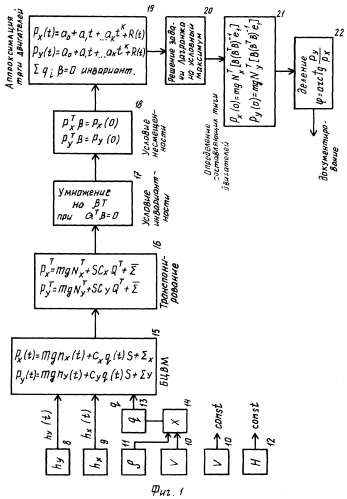
Предлагаемый способ поясняется фиг.1 и 2.

На фиг.1 представлена структурная схема алгоритма расчета суммарной тяги двигателя.

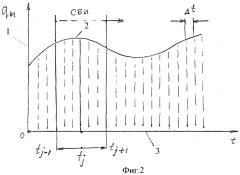
На фиг.2 представлен график изменения параметров аэродинамического напора и других измеряемых параметров 1 в скользящем базовом интервале 2, содержащем (2·l+1) измерений времени (t_-l…t₀…t_l) 3.

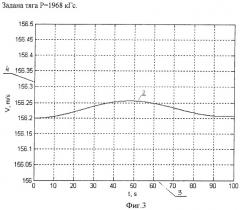
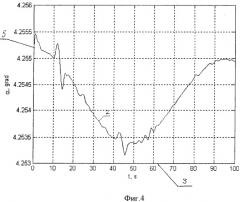
На фиг.3, 4, 5, 6 представлены графики измеренных параметров скорости полета v_m/s, угла атаки α_grad, величин перегрузок по осям X, Y n_y, n_x (1, 4, 5, 6) в течение 100 с интервала времени при заданной тяге Р=1968 кГс.

На фиг.7 показаны результаты расчета суммарной тяги двигателя P_∑ в течение 100 с полета.

Способ осуществляется следующим образом:

Способ определения тяги двигателя по результатам измерения в полете вектора состояния ЛА использует уравнения движения ЛА в продольной плоскости, инвариантные линейные преобразования измерений (см. фиг.1)

где Р_x и Р_y - проекции вектора тяги на связанные оси координат X, Y, которые определяются в виде:

Проекции вектора тяги на оси X, Y в зависимости от времен t выражаются в виде:

где q_изм - измеренные значения, содержащие случайные ошибки ε_x, ε_y.

Измерения выполняются в дискретные равноотстоящие моменты времени t_i(i=l…N) с шагом h=Δt (см. фиг.2). В результатах измерений выделяется скользящий базовый интервал (СБИ), содержащий (2·l+1) (обычно l≤5) измерение, отсчет времени выполняется от его середины Тогда уравнение для каждой точки СБИ в матричных обозначениях будет:

где

На небольшом скользящем базовом интервале C=const для каждого скользящего интервала. При матричном транспонировании указанных выражений получим:

Вводя в рассмотрение вектор неизвестных коэффициентов и умножая справа каждые члены уравнений на вектор β, получим:

На выбор элементов вектора β наложим условия инвариантности Q^Tβ=0 и несмещенности:

где и - значения сил тяги двигателей в средней точке СБИ.

Изменения тяги двигателя на интервале [t_-j,t_j] может быть приближенно представлено в виде разложения в ряд Тейлора:

где R_x(t), R_y(t) - остаточные члены разложения.

Для скользящего базового интервала условие несмещенности представляется в виде:

Приравнивая выражения при коэффициентах α в левой и правой частях данного выражения, найдем:

К этим условиям добавим условие инвариантности:

На выбор β накладывается условие минимума дисперсии

Определение оценки является решением задачи Лагранжа с введением в рассмотрение функции Лагранжа

Получаем значения сил тяги двигателей в средней точке СБИ:

где

λ₀…λ_k+1 - множители Лагранжа.

Величина суммарной тяги двигателей вычисляется как:

Угол между вектором Р_x и продольной осью самолета (направление вектора тяги) определяют в виде:

Пример

Для измерения суммарной тяги двигателей летательных аппаратов осуществляют измерение параметров в полете. На фиг.2-6 представлены графики измеренных параметров q_m, v_m/s, α_grad, n_y, n_x (1, 4, 5, 6) в течение 100 с интервала времени при заданной тяге Р=1968 кГс. С помощью БЦВМ обеспечивают автоматизированный цифровой анализ путем последовательного считывания каждой кривой измерений с небольшого скользящего базового интервала, включающего (2l+1) измерения. Рассчитывают суммарную тягу двигателей по алгоритму, приведенному на фиг.1. Результаты расчета суммарной тяги показаны на графике (см. фиг.7). Сравнение значений заданной и расчетной тяги Р_∑ показывает на удовлетворительную оценку сходимости результатов.

Способ автоматизированной оценки в полете суммарной тяги двигателей летательного аппарата (ЛА), включающий измерения самолетными датчиками - акселерометрами продольной и нормальной перегрузок в центре масс летательного аппарата, скоростного напора q, скорости полета V ЛА в дискретные равноотстоящие моменты времени Δt, отличающийся тем, что проводят комплекс измерений продольной и нормальной перегрузок, скоростного напора на неустановившихся режимах полета, в которых скоростной напор воздушного потока изменяется быстро по отношению к исходному в балансировочном режиме, в качестве которого принимают горизонтальный полет на постоянной высоте и средней скорости для этих высот, затем, используя аэродинамические соотношения с учетом случайной погрешности ε, обеспечивают автоматизированный цифровой анализ с помощью бортовой цифровой вычислительной машины путем последовательного считывания каждой кривой измерений с небольшого скользящего базового интервала (СБИ), включающего 2l+1 измерений, каждого из рассматриваемых параметров, определяют значения проекций вектора тяги по осям координат X, Y из следующих соотношений: причем для определения указанных значений P_x(t) и P_y(t) вводят при обработке измерений скользящий базовый интервал (СБИ), содержащий 2·l+1 (обычно l≤5), измерений каждого из рассматриваемых параметров такого, что где - коэффициенты сил лобового сопротивления и подъемной силы приведены в скоростной системе координат; α - угол атаки; m - масса ЛА; g - ускорение силы тяжести; S - площадь крыла; C_x, C_y - коэффициенты аэродинамических сил лобового сопротивления и подъемной силы в связанных осях координат ε_x, ε_y - случайные ошибки,полученные изменения тяги двигателя на интервале [t_-j,t_j] представляют в виде: где R_x(t), R_y(t) - остаточный член разложения тяги в ряд по степеням k, результаты измерений на СБИ для упрощения вычислений представляют в матричном виде: где T - операция транспонирования в расчеты вводят вектор неизвестных коэффициентов в соответствии со способом инвариантной фильтрации, умножают данные выражения на вектор неизвестных коэффициентов накладывают на выбор элементов вектора β следующие условия: инвариантности Q^Tβ=0, несмещенности: где и - значения сил тяги двигателей в средней точке СБИ, минимума дисперсии ошибки а оценку β определяют путем решения задачи на условный экстремум введением функции Лагранжа где λ₀…λ_k - множители Лагранжа,определяют коэффициенты из условия минимума функции Лагранжа: для снижения дисперсии принимают: затем вычисляют оценку значений составляющих вектора тяги по осям X, Y в каждой точке СБИ: определяют величину суммарной тяги двигателя и угол между вектором P_Σ и продольной осью самолета где λ₀…λ_k+1 - множители Лагранжа.