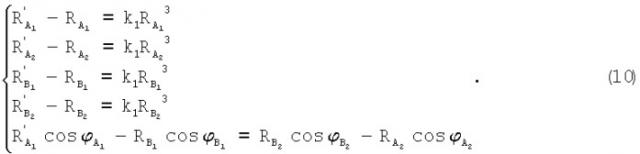Способ формирования панорамных изображений

Способ формирования панорамных изображений

Иллюстрации

Показать все

Реферат

Изобретение относится к вычислительной технике и может быть использовано для формирования панорамных изображений, лишенных искажений, вызванных радиальной дисторсией.

Известен способ получения панорамных изображений и устройство, его реализующее (патент США №5563650, H04N 7/18, от 08.10.1996). В основе способа лежит получение изображений с использованием камеры с объективом типа «fish eye» (объектив со сверхшироким углом обзора), последующее преобразование изображений в цифровой вид и трансформация в панорамные изображения, лишенные искажений, видимых человеческим глазом, с использованием компьютера и специального программного обеспечения.

Недостатками этого способа являются возможность применения данного способа только к заявленному устройству - камере с объективом типа «fish eye», соответственно узкая область применения, а также необходимость получения большого количества изображений для обеспечения высокой точности получения панорамных изображений.

Наиболее близким к предлагаемому является способ создания панорамных изображений в системах цифровых камер (патент США №6714249, H04N 7/00; G03B 17/00, от 30.03.2004), в котором заранее подготавливают и устанавливают в определенное положение камеру, поворачивая ее в предопределенные позиции, получают несколько серий перекрывающихся изображений (изображений с одинаковыми областями), сохраняют в памяти эти изображения и автоматически объединяют несколько изображений в панорамное изображение.

Недостатками этого способа являются получение панорамных изображений с низкой точностью из-за отсутствия коррекции аберраций оптических систем, а именно радиальной дисторсии, а также сложность практической реализации способа в связи с установкой камеры в строго определенное положение и поворота в предопределенные позиции.

Технической задачей изобретения является расширение области применения за счет использования минимального количества перекрывающихся изображений, без предварительной установки камеры в определенные позиции, повышение точности путем коррекции радиальной дисторсии.

Задача решается тем, что в известный способ получения панорамных изображений, включающий получение изображений с одинаковыми областями, преобразование изображений в цифровую форму, автоматическое соединение нескольких изображений в панорамное изображение, добавляют автоматическое выделение контуров на перекрывающихся изображениях, формирование множеств контуров для каждого изображения, определение множества контуров, идентичных на разных изображениях, и выбор двух калибровочных контуров из этого множества на основе математического аппарата нечеткой логики, вычисление центров тяжести калибровочных контуров на разных изображениях, расчет коэффициента радиальной дисторсии, автоматическую коррекцию искажений, вызванных радиальной дисторсией, поворот и смещение одного изображения относительно другого для формирования панорамного изображения.

Изобретение может быть использовано для формирования панорамных изображений из нескольких изображений, полученных цифровыми фото-, видеокамерами, с высокой точностью за счет автоматической корректировки искажений, вызванных радиальной дисторсией, и соответствует критерию «промышленная применимость».

Сущность изобретения поясняется чертежами, где на фиг.1 изображен алгоритм формирования панорамных изображений, на фиг.2 показан рисунок, поясняющий процесс коррекции радиальной дисторсии на изображениях, на фиг.3 представлен рисунок, поясняющий процесс идентификации контуров на двух изображениях.

Искажения, вызванные радиальной дисторсией, определяются [R.Y.Tsai «A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses», IEEE Trans, Rob. Autom, RA-3(4), pp.323-344, 1987] по формуле:

где (Δx_r, Δy_r) - отклонение точки изображения от ее истинного положения - положения, которое занимала бы точка при отсутствии радиальной дисторсии, k₁, k₂,…k_n - коэффициенты радиальной дисторсии, r=(x²+y²)^1/2 - расстояние от центра кадра до точки с координатами (х, y).

Согласно [Vark Reeves, Andrew J. Moore, Duncan P. Hand, Julian D.C. Jones «Dynamic shape measurement system for laser materials processing», Opt. Eng. 42(10), pp.2923-2929, 2003] для практического применения достаточно определять только коэффициент k₁.

Искажения, вызванные радиальной дисторсией в декартовой системе координат, исходя из (1), определяют по формулам:

Δх=х'-х,

Δy=y'-y,

y'-y=yk₁(x²+y²),

х'-x=xk₁(x²+y²),

в полярной системе координат:

R'-R=k₁R³,

где (х', y') - координаты точки, измеряемые по изображению.

Алгоритм формирования панорамных изображений представлен на фиг.1.

В блоке 1 (фиг.1) вводят два цифровых изображения с наличием одинаковых областей. Изображения получают с помощью цифровых фотокамер. Это происходит путем аналого-цифрового преобразования сигнала, характеризующего изображение, и сохранения изображений в цифровой форме в запоминающем устройстве фотокамеры.

Под изображением понимают матрицу значений яркостей пикселей цифрового изображения:

где x, y - координаты пикселя изображения по горизонтали и вертикали, соответственно, , , X, Y - размерность изображения по горизонтали и вертикали соответственно.

Следующие действия выполняет контроллер. После ввода изображений производят автоматическое выделение контуров объектов (блок 2, фиг.1) стандартным оператором, например, оператором Лапласа [Методы компьютерной обработки изображений. / Под. ред. В.А.Сойфера. - М.: Физматлит, 2001], и бинаризируют их. Для первого изображения формируют множество Z₁ контуров, а для второго - Z₂.

В блоке 3 (фиг.1) осуществляют определение множества идентичных контуров Q (контуров, соответствующих идентичным областям на обоих изображениях), причем:

Множество контуров Q состоит из элементов (контуров) Q_l:

,

где N_k - количество идентичных контуров.

Под контуром Q_l понимают совокупность отличных от фона изображения точек, таких, что для каждой точки (x_i, y_i) найдется не менее одной соседней точки (x_j, y_j), расположенной на расстоянии 1 пиксель:

.

Каждый контур описывается множеством из N_kl пар координат точек (x_i, y_i):

,

где N_kl - количество пар координат точек, составляющих контур.

Множество Q определяют с использованием нечеткой логики [Алтунин А.Е., Семухин М.В. Модели и алгоритмы принятия решений в нечетких условиях: Монография. Тюмень: Издательство Тюменского государственного университета, 2000]. Каждый контур множества Z₁ сравнивают с каждым контуром из множества Z₂. Контур описывается совокупностью внутренних и внешних, по отношению к контуру, параметров.

Для описания контура Q_l определяется множество векторов ν_ij с i-й точки T_i(x_i, y_i) контура на j-ю точку T_j(x_j, y_j) этого же контура:

ν_ij={d_ij,α_ij},

i=1…N_kl,

j=1…N_kl,

i≠j,

где d_ij - расстояние между точками T_i и T_j, α_ij - направление с i-й точки контура на j-ю точку.

Расстояние d_ij с учетом пропорционального увеличения контура равно:

Углом с i-й точки контура на j-ю точку считают угол между вертикальной осью изображения и направлением на j-ю точку (фиг.3). По теореме косинусов из треугольника ΔT_fT_iT_j:

Внешние параметры, аналогично внутренним, представляют множество векторов V_l, определяемых расстоянием d_l и направлением α_l на N_nr соседних контуров:

V_l={d_l,α_l},

,

где d_l, α_l определяются по формулам (5), (6) из треугольника ΔT_fT_iT_j (фиг.3), точки T_i, T_j являются центрами координат контура Q_l и соседнего для него контура.

Экспериментально установлен оптимальный диапазон значений N_nr∈[3;8]. При N_nr<3 могут быть неправильно сопоставлены контуры на разных изображениях, при

N_nr>8 существенно увеличиваются вычислительные затраты, тогда как вероятность правильного сопоставления контуров остается практически такой же, как и при N_nr=8.

Поиск идентичного контура на втором изображении осуществляют на основе функции принадлежности (ФП) µ_f2 терму «идентичный контур»:

µ_f2=µ_ид∧µ_идвн∧µ_sp,

где

µ_ид - ФП терму «внутренняя идентичность», по которой производят сравнения контуров по расположению составляющих каждый контур точек,

µ_идвн - ФП терму «внешняя идентичность», характеризующая схожесть контуров по взаимному расположению с соседними контурами,

µ_sp - ФП терму «яркостная идентичность», характеризующая идентичность контура по гистограмме распределения частот яркостей пикселей в прямоугольных областях, ограничивающих контур на изображениях.

ФП µ_ид равна:

,

при a=0.5. b=1, c=2.5,

при a=0.5. b=0.1, c=2.5,

где - разность расстояний между точками контура на разных изображениях, - разность величин углов между точками контура на разных изображениях, параметры а, b, с подобраны экспериментально.

ФП µ_идвн, характеризующая идентичность контура по множеству векторов внешних параметров, определяется как:

, при а=0.5, b=1, c=2.5,

, при а=0.5, b=0.1, с=2.5,

где - разность расстояний между контурами на разных изображениях, - разность величин углов на разных изображениях, параметры а, b, с подобраны экспериментально.

ФП µ_sp, характеризующая идентичность контура по гистограмме K(I_w) распределения частот яркостей пикселей в прямоугольных областях, ограничивающих контур на обоих изображениях, равна:

µ_sp=(1+(а(b-r))^c)^-1, при а=1.5, b=1, с=5,

,

где W(I₁), W(I₂) - количество точек с яркостями I₁ и I₂ на первом и втором изображениях соответственно, параметры a, b, с подобраны экспериментально.

Если рассматриваемому контуру Q_l не найден идентичный на втором изображении, его не включают во множество Q.

После определения множества идентичных контуров в блоке 4 (фиг.1) производят выбор двух калибровочных контуров из множества Q на основе математического аппарата нечеткой логики.

Вводят лингвистическую переменную (ЛП) «калибровочный контур» для выбора двух калибровочных контуров из множества Q. Калибровочные контуры должны удовлетворять следующим условиям:

- иметь оптимальную площадь и размер, определяемый размером описанного вокруг объекта прямоугольника;

- находиться на оптимальном расстоянии от края изображения.

Функция принадлежности ЛП «калибровочный контур» µ_кк равна:

где

µ_s - функция принадлежности терму «оптимальная площадь»,

µ_w - функция принадлежности терму «оптимальное окно»,

µ_kp - функция принадлежности терму «оптимальное положение в кадре».

Функция принадлежности µ_s терма «оптимальная площадь», зависящая от площади контура S, равна:

µ_s=(1+e^-(S-5))^-1,

Функция принадлежности µ_w терма «оптимальное окно» определяется размерами по горизонтали и вертикали описанного вокруг объекта прямоугольника:

µ_w=µ_wx∧µ_wy,

, при а=6.8, b=1.5,

,

где W_x, W_y - размеры описанного вокруг контура прямоугольника по горизонтали и вертикали соответственно, параметры a, b подобраны экспериментально.

ФП µ_kp терму «оптимальное положение в кадре» позволяет выбрать контуры, расположенные близко к краю кадра, и равна:

µ_kp=µ_kx∧µ_ky,

,

,

при

а₁=0.2,

b₁=0.05,

a₂=0.8,

b₂=0.07,

где (х, y) - координаты центра описанного вокруг контура прямоугольника, параметры а, b подобраны экспериментально.

После выбора двух калибровочных контуров Q₁ и Q₂, удовлетворяющих указанным выше условиям, в блоке 5 (фиг.1) производят определение центральной точки (ЦТ) каждого калибровочного контура на первом и на втором изображениях. В качестве ЦТ выбирается точка изображения, являющаяся центром тяжести [Дегтярев С.В., Садыков С.С., Тевс С.С., Ширабакина Т.А. Методы цифровой обработки изображений: Учебное пособие. Ч.1 / Курск. Гос. Техн. Ун-т. Курск, 2001] калибровочного контура и определяемая средними координатами всех его точек по горизонтали и вертикали. Обозначают ЦТ контура Q₁ на первом изображении точкой , на втором - , ЦТ контура Q₂ на первом изображении - точкой , на втором - .

Т.к. в пространстве расстояние между объектами, которые описаны калибровочными контурами Q₁ и Q₂, не менялось во время получения первого и второго изображений, то и на изображениях без учета искажений радиальной дисторсии проекция этих расстояний на ось абсцисс будет постоянной (фиг.2):

,

,

,

,

,

,

,

,

где , , , - точки на искаженном радиальной дисторсией изображении, соответствующие точкам A₁, B₁, A₂, В₂, чьи координаты рассчитывают в блоке 5 (фиг.1).

В блоке 6 (фиг.1) производят расчет коэффициента радиальной дисторсии.

На основе формул (2), (9) составляют систему уравнений:

Первые четыре уравнения из системы (10) являются кубическими уравнениями (если их решать относительно R) и имеют корни [И.Н.Бронштейн, К.А.Семендяев. Справочник по математике. Издание седьмое, стереотипное. М.: гос. изд-во технико-теоретической лит-ры, 1957, с.138], которые вычисляют:

Подставив корни (11-14) первых четырех уравнений системы (10) в последнее уравнение, получают:

Уравнение (15) с одной неизвестной k₁ решают численными методами [Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Наука. Гл. ред. физ.-мат. лит., 1966].

После нахождения коэффициента радиальной дисторсии производят автоматическую коррекцию (блок 7, фиг.1) изображений путем расчета истинных координат всех точек для каждого изображения, используя формулу (1), и восстановления истинных положений этих точек.

После того, как получают изображения со скорректированной радиальной дисторсией, в блоке 8 (фиг.1) рассчитывают угол поворота одного изображения относительно другого для последующего корректного соединения изображений с целью создания панорамного. Для этого вычисляют угол наклона ξ₁ прямой, проходящей через точки А₁, В₁, к оси абсцисс на первом изображении и угол наклона ξ₂ прямой, проходящей через точки А₂, В₂, к оси абсцисс на втором изображении по формулам:

Вычисляют разность углов Δξ:

По формулам (16) и (17) рассчитывают угол, на который поворачивают второе изображение, используя формулы аффинного преобразования на плоскости, а именно поворота относительно начала координат на угол γ:

Если Δξ=0, то поворот не выполняется.

Затем в блоке 9 (фиг.1) рассчитывают расстояние h, на которое затем смещают второе изображение, по формуле:

В случае соединения по горизонтали двух изображений для получения панорамных u и ν вычисляют по формулам:

где X₁, X₂ - размерность первого и второго изображений по горизонтали соответственно.

В случае соединения по вертикали двух изображений для получения панорамных u и ν рассчитывают по формулам:

где Y₁, Y₂ - размерность первого и второго изображений по вертикали соответственно.

Используя формулы аффинного преобразования переноса вдоль оси абсцисс на плоскости, осуществляют перенос второго изображения по направлению к левому краю или к нижнему краю, в зависимости от направления соединения, изображения на расстояние h, определяемое по формуле (19).

В блоке 10 (фиг.1) выполняют соединение первого и второго изображения с целью формирования панорамного изображения.

При получении панорамного изображения, имея n исходных изображений, последовательность действий, рассмотренных в способе, выполняется n-1 раз.

Рассмотрим варианты реализации предложенного способа:

1. Получают изображения цифровой фотокамерой, изображения сохраняют в памяти фотокамеры, определение коэффициента и коррекцию радиальной дисторсии производят с использованием контроллера фотокамеры, осуществляют ввод изображений в ЭВМ через USB-порт, формирование панорамных изображений производит ЭВМ;

2. Получают изображения цифровой фотокамерой, изображения сохраняют в памяти фотокамеры, осуществляют ввод изображений в ЭВМ через USB-порт, определение коэффициента и коррекцию радиальной дисторсии, а также формирование панорамных изображений производит ЭВМ;

3. Получают изображения цифровой фотокамерой, изображения сохраняют в памяти фотокамеры, последовательность действий, предложенную в рамках данного способа, выполняет контроллер фотокамеры, панорамные изображения сохраняются в памяти фотокамеры.

Таким образом, изобретение позволяет повысить точность формирования панорамных изображений, которая достигается коррекцией радиальной дисторсии, а также расширить область применения за счет использования минимального количества перекрывающихся изображений, без предварительной установки камеры в определенные позиции.

Способ формирования панорамных изображений, включающий получение одинаковых изображений нескольких областей панорамных изображений посредством фото или видеокамер, аналого-цифровое преобразование сигналов, характеризующее полученные изображения, и сохранение их в запоминающем устройстве, соединение цифровых изображений в панорамное изображение в виде матрицы пикселей, отличающийся тем, что для каждого панорамного изображения выделяют на матрице пикселей контура из совокупности точек изображения, отличных от фона изображения на перекрывающихся изображениях, формируют множества контуров для каждого панорамного изображения, определяют множество контуров, идентичных на разных панорамных изображениях, и выбирают два калибровочных контура из этого множества на основе математического аппарата нечеткой логики, вычисляют центры тяжести калибровочных контуров на разных изображениях, рассчитывают коэффициент радиальной дисторсии, корректируют искажения, вызванные радиальной дисторсией, поворачивают и смещают одно изображение относительно другого для получения панорамного изображения, характеризующегося высокой точностью.