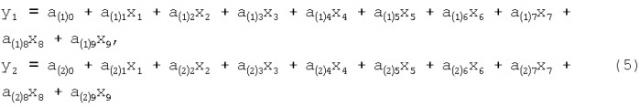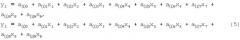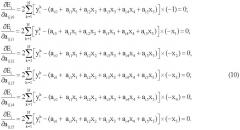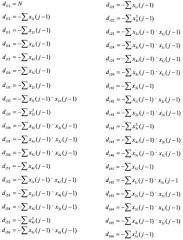Способ автоматического управления процессом разложения тетракарбонила никеля (ткн) в аппарате с электрическим нагревом стенок

Способ автоматического управления процессом разложения тетракарбонила никеля (ткн) в аппарате с электрическим нагревом стенок

Иллюстрации

Показать все

Реферат

Изобретение относится к способам автоматического управления технологическими процессами, в частности к системе управления процессом разложения тетракарбонила никеля в полом цилиндрическом аппарате.

В России на данный момент не было работающей системы автоматического управления процессом разложения тетракарбонила никеля. Используется ручное управление согласно технологическому регламенту (инструкции). В технологической инструкции указаны жесткие пределы температуры внутри корпуса, а также границы управляющих воздействий (температуры нагревателей), за которые выходить нельзя.

Данный процесс представляет сложность для управления, а тем более для создания системы автоматического управления, поскольку процесс стохастический, т.е. непрерывно изменяется, и при одних и тех же условиях протекания процесса на выходе возможно получение никелевого порошка с различными показателями качества. Кроме того, пока не придуман способ получения непрерывных достоверных показателей качества порошка. Таким образом, соблюдение технологической инструкции не дает гарантии получения порошка необходимого качества.

Кроме того, существует способ автоматического управления разложением тетракарбонила никеля, основанный на модели, рассчитанной по экспериментальным данным. Коэффициенты данной модели рассчитаны заранее и автоматически не корректируются. Кроме того, следует отметить, что, создавая модель на достаточно большой диапазон возможных значений параметров процесса, ухудшается ее точность. Данная модель контролирует температуру процесса (температуру внутри корпуса разложителя) и пытается стабилизировать ее. Происходящие возмущения системой не отслеживаются напрямую, а фиксируется при изменении температуры процесса, которая стабилизируется за счет изменения расхода топлива. Кроме того, показателем качества данной системы является только насыпной вес никелевого порошка, в ней не учитывается средний диаметр частиц, что не позволяет получить полностью кондиционный никелевый порошок. Данное решение является наиболее близким к предлагаемому техническому решению, поэтому принимаем его за прототип. (Автоматическое управление процессом разложения карбонила никеля; В.А.Иванов, Д.И.Лисовский, В.В.Стопкевич; Бюллетень ЦИИНЦветМет «Цветные Металлы» №21, 1966 г.)

Целью предлагаемого изобретения является устранение недостатков прототипа, т.е. повышение качества получаемого никелевого порошка в процессе разложения тетракарбонила никеля, используя целевую функцию:

где Ves^*, Fisher^* - заданные значения показателей качества;

Ves, Fisher - прогнозируемые показатели качества;

ω₁, ω₂ - весовые коэффициенты (ω₁+ω₂=1), задаваемые мастером-технологом.

Под качеством никелевого порошка понимают товарные показатели качества: насыпной вес (Ves) и средний диаметр частиц (Fisher).

Для решения этой задачи используется способ автоматического управления процессом разложения тетракарбонила никеля (ТКН) в аппарате с электрическим нагревом стенок, включающий регулирование температуры участков внешней стенки аппарата, отличающийся тем, что

- одновременно измеряют и стабилизируют температуры стенки аппарата по зонам нагрева,

- формируют статистическую модель следующего вида:

где Ves - насыпной вес никелевого порошка;

Fisher - средний диаметр частиц никелевого порошка;

Т_к1…6 - температура корпуса в зонах 1-6 (предварительные задания локальным контурам стабилизации);

Р_ТКН - давление Ni(CO)₄ в разложителе;

Q_CO - расход СО в разложителе;

Р_O2 - давление кислорода в разложителе;

а₁₀…а₂₉ - коэффициенты модели,

- измеряют температуру воздуха в цехе, температуру и расход оборотного СО,

- затем непрерывно корректируют рассчитанные по статистической модели и отвечающие целевой функции задания локальным контурам стабилизации по температуре воздуха в цехе, по температуре и расходу оборотного СО, используя выражения:

где i=1,2,3…n;

- температура нагрева в i-той зоне (скорректированное задание локальным контурам стабилизации);

- величина коррекции первоначального задания в i-той зоне;

T_Ki - первоначальное задание нагревателю в i-той зоне, удовлетворяющее целевой функции, рассчитанное по модели (2);

T_mi(j) - температура материала в j-той зоне;

T_ki(j) - температура корпуса в j-той зоне;

T_mi(j-1) - температура материала в (j-1)-той зоне;

T_mi-i(j-1) - температура материала в (j-1)-той зоне в предыдущий момент времени;

T_CO(j-1) - температура оборотного СО в (j-1) зоне;

Q_CO(j-1) - расход оборотного СО в (j-1) зоне;

T_OC(j-1) - температура окружающей среды в (j-1) зоне;

а₁₀…а₆₅ - коэффициенты модели,

- прогнозируют текущие показатели качества процесса по следующим формулам:

где:

- прогнозное значение насыпного веса;

- прогнозное значение среднего диаметра частиц;

x₁…x₆=Т_к1…6 - температура корпуса в зонах 1-6;

х₇=Р_ТКН - давление Ni(CO)₄ в разложителе;

x₈=Q_CO - расход СО в разложителе;

x₉=Р_O2 - давление кислорода в разложителе,

- а полученные значения , подают в качестве задания на регулирование температуры участков внешней стенки аппарата.

В предлагаемом способе используется как аналоговая информация, принимаемая с датчиков, расположенных на аппарате, так и дискретная информация, вводимая вручную по результатам анализа конечного продукта. Алгоритм управления позволяет решать поставленную задачу при минимуме воздействий, так как оценка необходимости принятия решений производится через достаточно большой промежуток времени. Кроме того, чтобы избежать резких изменений заданий исполнительным механизмам, рассчитанные с помощью оптимизационной задачи температуры корпуса в разных зонах печи корректируются в зависимости от величины их разности с предыдущими значениями и от того, один или оба показателя качества процесса отличаются от своих заданных значений более чем на допустимую величину.

Работа предлагаемого изобретения производится следующим образом: собирается база данных нормальной эксплуатации за 48 часов с дискретностью 5 минут, далее производится расчет коэффициентов математической модели по формулам (2), (3) и (4).

Используем следующие обозначения в формуле (2):

у₁=Ves;

у₂=Fisher;

x₁…х₆=T_k1…T_k6;

х₇=Р_ТКН;

х₈=Q_CO;

х₉=P_O2.

Тогда система уравнений примет вид:

Поиск значений коэффициентов этих уравнений осуществляется методом наименьших квадратов. Для этого нужно минимизировать сумму квадратов отклонений

Приравняв к нулю частные производные по коэффициентам a_(i)j, получим следующую систему уравнений:

Перепишем эти уравнения, введя следующие обозначения:

Тогда система уравнений запишется как:

где

a_i=(a_0i, a_1i, a_2i, a_3i, a_4i, a_5i, a_6i, a_7i, a_8i, a_9i,)^T

B=(b_0i, b_1i, b_2i, b_3i, b_4i, b_5i, b_6i, b_7i, b_8i, b_9i,)

Уравнение (7) решается методом Гаусса, заключающимся в приведении матрицы D_i к треугольному виду.

Используем следующие обозначения для формулы (3):

Тогда уравнения (4) перепишутся следующим образом:

Поиск значений коэффициентов этих уравнений осуществляется методом наименьших квадратов. Для этого нужно минимизировать сумму квадратов отклонений:

где N - число измерений, i=1…6.

Приравняв к нулю частные производные по коэффициентам a_(i)j, получим следующую систему уравнений:

Перепишем эти уравнения, введя следующие обозначения:

Тогда система уравнений запишется как:

где

a_i=(a_0i, a_1i, a_2i, a_3i, a_4i, a_5i)^T

B=(b_0i, b_1i, b_2i, b_3i, b_4i, b_5i)

Уравнение (11) решается методом Гаусса.

Поиск значений коэффициентов для уравнений (4) осуществляется методом наименьших квадратов. Для этого нужно минимизировать сумму квадратов отклонений

Приравняв к нулю частные производные по коэффициентам a_(i)j, получим следующую систему уравнений:

Введем следующие обозначения:

Тогда система уравнений запишется как:

где

a_i=(a_0i, a_1i, a_2i, a_3i, a_4i, a_5i, a_6i, a_7i, a_8i, a_9i,…a_55i)^T

B=(b_0i, b_1i, b_2i, b_3i, b_4i, b_5i, b_6i, b_7i, b_8i, b_9i,b_54i)

Уравнение (14) решается методом Гаусса.

После этого производится расчет текущих показателей качества по формуле (4), используя полученные коэффициенты модели и текущие параметры процесса. Если эти значения отличаются от заданных на величину большую, чем допуск, производится расчет управляющих воздействий по формуле (1), подставляя в нее рассчитанные коэффициенты модели и необходимые показатели качества и используя целевую функцию (2). Далее производится коррекция рассчитанных значений по формуле (3). Рассчитанные значения температур корпуса в различных зонах проверяются на соответствие допустимым пределам:

где Т_ki - рассчитанное значение температуры корпуса в i-зоне;

- минимальное значение температуры корпуса в i-зоне;

- максимальное значение температуры корпуса в i-зоне.

Если значения рассчитанных температур выходят за допустимые пределы, то они принимаются равными предельным значениям и вновь производится решение оптимизационной задачи по формулам (1), (2) и (3) с пятью варьируемыми температурами, затем, при необходимости, с четырьмя и т.д.

После этого, чтобы избежать резких изменений заданий исполнительным устройствам, рассчитывается величина коррекция текущих температур по зонам в зависимости от разности вновь вычисленной и предыдущей температуры и от того, один или оба показателя качества отличаются от заданных более чем на допустимую величину. Если оба показателя качества находятся вне допустимой зоны относительно заданного значения, величина коррекции определяется как

T'=ΔT/k,

где ΔТ - разность текущей и вновь вычисленной температуры данной зоны,

k - настроечный параметр.

При недопустимом отклонении от заданного значения только насыпного веса коррекция температур рассчитывается как

T'=ΔT/k+1,

где ΔT - разность текущей и вновь вычисленной температуры данной зоны,

k, 1 - настроечные параметры.

И в последнем случае, когда вне допустимой зоны находится только значение показателя Fisher, величина коррекции равна

T'=ΔT/k+m,

где ΔT - разность текущей и вновь вычисленной температуры данной зоны,

k, m - настроечные параметры.

(k,l,m - нормативные величины, являющиеся настроечными параметрами, 1<m).

Численный пример

Возьмем базу данных с 25.04.2006 6:39 по 25.04.2006 7:14

Время	6:39	6:44	6:49	6:54	6:59	7:04	7:09	7:14
Вес	0,034	0,19	0,19	0,19	0,19	0,19	0,19	0,19
Фишер	2,51	2,51	2,51	2,51	2,51	2,51	2,51	2,51
Ткор1	536,7	536,7	536,3	533,7	533,5	531,9	530,8	530,5
Ткор2	521,1	520,7	518,5	517,9	517,6	516	514,9	514,5
Ткор3	420,6	420	418,4	417,7	417,3	416,9	415	414,6
Ткор4	406	405,4	405	404,8	404,6	402,3	402,1	401,3
Ткор5	305	304,6	304,7	302,8	301,9	301,9	301,6	301,3
Ткор6	300,9	300,2	300,2	299,8	299,5	297,7	297	296,6
Тмат1	267,5	266,3	265,5	264,6	263,7	262,8	261,7	260,7
Тмат2	274,7	273,8	272,6	272,1	270,9	269,8	269,3	268
Тмат3	267,7	266,3	266	264,9	264,2	263,3	262,5	261,6
Тмат4	257,7	256,8	256,4	255,4	254,7	253,8	253,1	252,2
Тмат5	237	236,3	235,4	234,9	234,2	233,3	232,4	231,8
Тмат6	209,5	208,1	207,8	207,2	206,4	206	204,8	204,1
РасхСО	6,1	5,9	6,7	6,9	6,9	7,5	7,1	7,3
ДавлO2	0,2	0,199	0,198	0,198	0,197	0,196	0,195	0,195
ДавлТКН	0,034	0,033	0,034	0,035	0,034	0,035	0,034	0,035
Расх об СО	121,5	120,4	118,5	119,9	118,8	120,3	121,6	121,5
Т об СО	26,3	26	25,4	25,3	25	25	24,3	24,2
Тос	10,06	10,06	10,2	10,25	10,25	10,45	10,16	10,25

Для модели (2) по формуле (7) рассчитаем коэффициенты

	Вес	Фишер
своб	-0,159614551	2,966396298
Ткор1	0,000339887	6.81055Е-07
Ткор2	0,000228099	-0,003440634
Ткор3	0,002550118	0,00319666
Ткор4	-0,002334715	0,003433622
Ткор5	-0,001831462	-0,01445
Ткор6	0,001514299	0,010088988
РасхСО	-0,000756139	-0,002119386
ДавлO2	0,220661353	0,377208688
ДавлТКН	0,965923275	3,392790128

По формуле (2) получаем прогноз Вес - 0,227, Фишер - 2,715.

Более точный прогноз по формулам (4) дает следующие результаты: Вес - 0,217,

Фишер - 2,696, что при заданных значениях (и допусках) для Веса 0,18 (0,02) и Фишера 2,5 (0,15) требует расчета новых значений температур корпусов.

По формуле (2) рассчитаем новые значения температур корпусов, используя целевую функцию (I):

Ткор1=526,84;

Ткор2=498,32;

Ткор3=418,31;

Ткор4=406,02;

Ткор5=301,31;

Ткор6=280,86.

Производим проверку вхождения рассчитанных температур корпусов в установленные пределы:

Температура Ткор2 ниже нижней границы (500), таким образом, Ткор2=500.

Произведем перерасчет температур:

Ткор1=526,84;

Ткор2=500;

Ткор3=416,75;

Ткор4=406,53;

Ткор5=300,60;

Ткор6=280,18.

Коррекция рассчитанных новых значений температур корпусов по формулам (3) составит:

ΔТкор1=0,86;

ΔТкор2=-0,13;

ΔТкор3=0,06;

ΔТкор4=0,45;

ΔТкор5=0,31;

ΔТкор6=-0,03.

Таким образом, скорректированные значения температур корпусов составят (коррекция по Ткор2 опять выведет Ткор2 за допустимые пределы, поэтому Ткор2 остается равной нижней границе):

Ткор1=527,7;

Ткор2=500;

Ткор3=416,81;

Ткор4=406,98;

Ткор5=300,91;

Ткор6=280,15.

Далее производится пошаговая передача рассчитанных управляющих воздействий на исполнительные механизмы:

	Шаг 1	Шаг 2	Шаг 3
Ткор1	529,5667	528,6333	527,7
Ткор2	509,6667	504,8333	500
Ткор3	415,3367	416,0733	416,81
Ткор4	400,5267	399,7533	398,98
Ткор5	296,5033	291,7067	286,91
Ткор6	291,1167	285,6333	280,15

Прогнозные значения показателей качества для рассчитанных (конечных) значений составят:

Вес=0,194;

Фишер=2,641.

Таким образом, обеспечивается выполнение целевой функции.

Краткое описание чертежей

На чертеже изображена схема системы автоматического управления процессом разложения ТКН. Информация о текущих параметрах процесса: насыпной вес и средний диаметр частиц никелевого порошка (10), текущая температура корпуса разложителя по зонам (14.1-14.6), давление Ni(CO)₄ в разложителе (11), давление О₂ (12) в разложителе, расход СО (13) в разложителе, поступают в математическую модель (3) процесса, которая в зависимости от значений этих параметров вырабатывает предварительные задания локальным регуляторам (15). Далее эти задания сравниваются с текущей температурой корпуса разложителя по зонам (14.1-14.6) и корректируются с учетом значений, полученных в блоке коррекции управления (4).

Расчет коррекции задания регулятору осуществляется в блоке коррекции управления (4), в который поступают текущие значения следующих параметров процесса: температура внутри корпуса разложителя по зонам от термопар (8), расход и температура оборотного СО (9), температура воздуха в цехе, вблизи нижней нефутерованной зоны от датчика температуры (7).

После этого скорректированные задания поступают на регулятор (5), который через задания нагревателям (16.1-16.6) устанавливает необходимые значения температуры корпуса разложителя по зонам, обеспечивающие минимальные отклонения показателей качества от заданных значений.

Способ автоматического управления процессом разложения тетракарбонила никеля (ТКН) в аппарате с электрическим нагревом стенок, включающий регулирование температуры участков внешней стенки аппарата, отличающийся тем, чтоодновременно измеряют и стабилизируют температуры стенки аппарата по зонам нагрева,формируют статистическую модель следующего вида где - насыпной вес никелевого порошка; - средний диаметр частиц никелевого порошка;Т_к1…6 - температура корпуса в зонах 1-6 (предварительные задания локальным контурам стабилизации);Р_ткн - давление Ni(CO)₄ в разложителе;Q_СО - расход СО в разложителе;Р₀₂ - давление кислорода в разложителе;а₁₀…а₂₉ - коэффициенты модели,измеряют температуру воздуха в цехе, температуру и расход оборотного СО,затем непрерывно корректируют рассчитанные по статистической модели и отвечающие целевой функции задания локальным контурам стабилизации по температуре воздуха в цехе, по температуре и расходу оборотного СО, используя выражения где i=1,2,3...n; - температура нагрева в i-й зоне (скорректированное задание локальным контурам стабилизации); - величина коррекции первоначального задания в i-й зоне;T_Ki - первоначальное задание нагревателю в i-й зоне, удовлетворяющее целевой функции, рассчитанное по модели (2);T_mi(j) - температура материала в j-й зоне;T_ki(j) - температура корпуса в j-й зоне;T_mi(j-1) - температура материала в (j-1)-й зоне;T_mi-i(j-1) - температура материала в (j-1)-й зоне в предыдущий момент времени;T_CO(j-1) - температура оборотного СО в (j-1) зоне;Q_CO(j-1) - расход оборотного СО в (j-1) зоне;T_OC(j-1) - температура окружающей среды в (j-1) зоне;а₁₀…а₆₅ - коэффициенты модели,прогнозируют текущие показатели качества процесса по следующим формулам: где - прогнозное значение насыпного веса; - прогнозное значение среднего диаметра частиц;x₁…x₆=Т_к1…6 - температура корпуса в зонах 1-6;х₇=Р_ткн - давление Ni(CO)₄ в разложителе;x₈=Q_CO - расход СО в разложителе;x₉=Р₀₂ - давление кислорода в разложителе,а полученные значения подают в качестве задания на регулирование температуры участков внешней стенки аппарата.