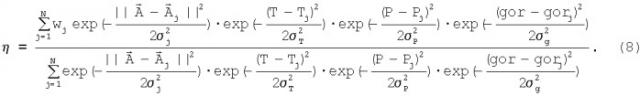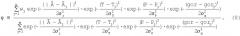Способ определения свойств пластовых флюидов

Способ определения свойств пластовых флюидов

Иллюстрации

Показать все

Реферат

Область техники

Настоящее изобретение относится к способам определения свойств пластов, окружающих подземную скважину, а точнее к способу определения свойств подземных пластовых флюидов. Изобретение может быть использовано для определения вязкости и/или молекулярного состава сырой нефти путем измерения ядерно-магнитного резонанса, выполненного на пробах подвижной нефти, собранных в пласте посредством скважинного пробоотборника.

Предшествующий уровень техники

Скважинные пробоотборники пластового флюида, часто называемые приборами для испытания пласта, предназначены для извлечения, а иногда и исследования проб флюидов из пластов. На этих пробах флюидов могут быть проведены необходимые измерения, когда прибор находится в скважине, и/или на пробах, которые после отбора поднимаются наверх.

Когда пробу флюида отбирают в зоне, содержащей углеводороды, она может быть использована для определения свойств углеводорода, например, вязкости и/или молекулярного состава. Однако возможности существующих способов для определения этих свойств ограничены. Например, вязкость может быть предсказана по демпфированию колебаний вибрирующего механического измерительного элемента прибора, но при таких измерениях в скважине необходимо, чтобы прибор работал в тяжелых окружающих условиях, которые не являются благоприятными для надежной и точной работы прибора. В приборе для испытания пласта может быть использован ядерно-магнитный резонанс (см., например, патент США №6111408), а измерения ядерно-магнитного резонанса пластовых флюидов могут дать информацию, по которой можно прогнозировать свойства флюидов. Поскольку нефтяные флюиды представляют собой сложные смеси, содержащие углеводородные молекулы различных видов, трудно сделать точное предсказание вязкости и состава для случая произвольных значений температуры (Т) и давления (Р). Один подход заключается в применении физических моделей или корреляций, которые связывают физическое свойство, подлежащее предсказанию, с результатами измерений ядерно-магнитного резонанса путем использования уравнения, содержащего параметры, определенные эмпирически.

Пример способа для предсказания вязкости пластовых флюидов по результатам ядерно-магнитного резонанса распределений времен (Т₁ и Т₂) релаксации и коэффициентов (D) диффузии основан на эмпирических корреляциях (см. Morriss et al., SPWLA Annual Transactions, стр.1-24, June 19-22, 1994; Freedman et al., SPE Journal (75325), December 2001; Lo et al., SPE Journal (77264), March 2002). Корреляции через эмпирически определенные постоянные связывают логарифмические средние распределений с вязкостью. Точность значений вязкости, предсказываемых по этим корреляциям, ограничена тремя факторами: 1) не учитывается детальная форма распределений; 2) эмпирические постоянные, используемые в корреляциях, не являются универсальными и могут изменяться для различных видов нефти более чем в два раза; 3) принятая форма для корреляционных уравнений точно не определена.

В скважинных приборах для отбора проб флюидов молекулярный состав может быть весьма грубо оценен путем использования результатов измерений оптической плотности в зависимости от длины волны при излучении в ближней инфракрасной области (см. Fujisawa et al., SPE 84092, представлено на конференцию SPE ATCE, 2003). Для предсказания молекулярной группировки, то есть С₁, С₂-С₅ и С₆+, в способе использован регрессионный анализ главных компонентов. Были предложены основанные на физических процессах параметрические модели, предназначенные для предсказания молекулярного состава сырой нефти по результатам ядерно-магнитных резонансных измерений распределений времен релаксации и коэффициентов диффузии (см. Heaton and Freedman, публикация патента США, 2003-0128032-А1). Однако, используя физические модели, трудно учесть различные формы молекул, например, молекул ароматических и алифатических углеводородов, влияние давления и температуры и растворенных газов.

Краткое изложение сущности изобретения

Задачей настоящего изобретения является создание способа определения характеристик пластового флюида, в котором исключены недостатки известных способов.

Настоящее изобретение относится к способу определения свойств флюидов в пластах, окружающих подземную скважину. Один вариант осуществления способа изобретения включает в себя следующие этапы: создание на основании измерений на большом количестве проб флюида базы данных из запомненных обучающих значений свойств флюида, связанных с запомненными обучающими значениями измерений флюида; получение из указанной базы данных параметров радиальной базисной функции, таких как вес и ширина; получение значений измерений пластового флюида; и определение путем использования интерполяции с помощью радиальной базисной функции указанного свойства пластовых флюидов из значений в указанной базе данных, указанных параметров и указанных полученных значений измерений пластового флюида.

В предпочтительном варианте осуществления изобретения этап получения из указанной базы данных параметров ширины и веса радиальной базисной функции содержит образование отображающей функции радиальной базисной функции; образование функции стоимости путем использования значений из базы данных и отображающей функции; и минимизацию указанной функции стоимости, чтобы определить указанные параметры веса и ширины.

В варианте осуществления изобретения указанный этап создания по измерениям на большом количестве проб флюида базы данных из запомненных обучающих значений свойств флюида, связанных с запомненными обучающими значениями измерений флюида, содержит создание базы данных из запомненных обучающих значений вязкости флюида, связанных с запомненными обучающими значениями ядерно-магнитного резонанса флюида, при этом указанный этап получения значений измерений пластового флюида содержит получение значений измерений ядерно-магнитного резонанса по флюиду, отобранному из указанных пластов, при этом этап определения свойства пластовых флюидов содержит определение вязкости пластовых флюидов.

В других вариантах осуществления изобретения определяемое свойство пластовых флюидов представляет собой соотношение газ/нефть для пластовых флюидов, молекулярный состав пластовых флюидов, плотность в жидком состоянии пластовых флюидов или давление насыщения пластовых флюидов.

Изобретение может быть использовано в так называемых спускаемых на кабеле скважинных каротажных устройствах для испытания пластов, в которых флюиды извлекаются из подземных пластов, но также может быть использовано в других ситуациях, например, при измерениях в процессе бурения или при измерениях в процессе cпуско-подъемных операций.

Краткое описание чертежей

Дополнительные признаки и преимущества настоящего изобретения поясняются нижеследующим подробным описанием со ссылками на сопровождающие чертежи, на которых:

фиг.1 изображает схему каротажного устройства для испытания пласта, размещенного в скважине, согласно изобретению;

фиг.2 - осевое сечение части ядерно-магнитного устройства для размещения в потоке, которое может быть использовано при осуществлении изобретения;

фиг.3 - диаграмму обучающего и тестового распределений упрощенного примера с интерполяцией, согласно изобретению;

фиг.4 - диаграмму, иллюстрирующую интерполяцию с помощью радиальной базисной функции для трех различных параметров ширины, согласно изобретению;

фиг.5А и 5В - схему последовательности этапов реализации способа, согласно изобретению;

фиг.6А и 6В - схему последовательности операций для реализации этапа 510 на фиг.5А, относящегося к получению базы данных из результатов измерений «входная величина - выходная величина», согласно изобретению;

фиг.7 - диаграмму зависимости амплитуды от Т₂ для обучающих и тестовых распределений, согласно изобретению;

фиг.8 - графическое представление для данных из примера на фиг.7 вязкости, предсказанной для каждого тестового распределения путем использования уравнения (8), в сопоставлении с истинной вязкостью, вычисленной на основании уравнения (6), согласно изобретению;

фиг.9А-Р - диаграммы распределений Т₂ для шестнадцати проб из таблицы 1, использованных в примере, согласно изобретению;

фиг.10 - диаграмму вязкости, предсказанной путем использования способа, согласно изобретению, в сопоставлении с измеренной вязкостью для примера с использованием шестнадцати проб из таблицы 1, согласно изобретению;

фиг.11 - диаграмму вязкости, предсказанной путем использования способа из предшествующего уровня техники, в сопоставлении с измеренной вязкостью для примера с использованием шестнадцати проб из таблицы 1, согласно изобретению;

фиг.12А - диаграммы зависимостей мольных концентраций от молекулярной массы для истинного и предсказанного составов согласно примеру с использованием модельных данных, согласно изобретению;

фиг.12B1-16 - диаграммы для каждой из шестнадцати проб из примера зависимостей мольных концентраций от углеродного числа для предсказанных составов и для жидких составов, быстро испаренных в результате газовой хроматографии (ГХ), согласно изобретению;

фиг.13А-Р - диаграммы нормированных оконных сумм для шестнадцати проб примера, и

фиг.14А-Р - диаграммы зависимостей мольной концентрации от углеродного числа как для предсказанных составов, так и для жидких составов, быстро испаренных в результате газовой хроматографии (ГХ), в этом случае предсказанные составы основаны на нормированных оконных суммах, согласно изобретению.

Подробное описание предпочтительных вариантов воплощения изобретения

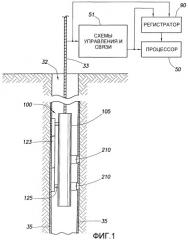
На фиг.1 показана скважина 32, которая пробурена известным способом посредством бурового оборудования и при использовании промывочной жидкости или бурового раствора, в результате чего образовалась глинистая корка 35. Устройство 100 для испытания пласта может быть использовано при практическом осуществлении изобретения. Устройство 100 подвешено в скважине 32 на армированном многожильном кабеле 33, длина которого по существу определяет глубину погружения устройства 100. Для измерения перемещения кабеля по колесу (не показано) предусмотрено устройство (не показано) для измерения глубины, и следовательно, глубины погружения каротажного устройства 100 в скважине 32. Схемы 51 показаны на поверхности, хотя часть их обычно находится в скважине, и представляют собой схемы управления и связи, относящиеся к испытательной технике. На поверхности также расположены процессор 50 и блок 90 записи.

Устройство 100 имеет удлиненный корпус 105, в котором находятся скважинная часть установки, элементы управления, камеры, измерительные средства и т.д. Один или несколько рычагов 123 могут быть закреплены на поршнях 125, которые выдвигаются, например, при управлении с поверхности, для фиксации прибора. Устройство содержит один или несколько зондирующих модулей, каждый из которых содержит зондовый узел 210, который может быть перемещен посредством привода зонда (не показан отдельно) и который включает в себя зонд (не показан), который перемещается наружу в контакт со стенкой скважины, при этом он прокалывает глинистую корку и сообщается с пластом. Оборудование и способы для выполнения измерений давления и отбора проб пластового флюида известны в области техники, к которой относится изобретение, и каротажное устройство 100 снабжено этими известными средствами. Например, можно сослаться на патенты США №№3934468, 4860581 и 6346813.

Современные коммерческие службы, использующие, например, модульный динамический испытатель пластов MDT (“MDT” - товарный знак заявителя - Schlumberger), могут предоставлять разнообразные услуги по измерениям и отборам проб, поскольку прибор имеет модульную конструкцию и может быть конфигурирован рядом способов. В качестве примеров некоторых модулей, используемых в приборе такого типа, можно указать следующие. Обычно предусмотрен модуль электропитания. Он не имеет сборной линии или гидравлической шины и является первым (верхним) модулем в цепочке. Модуль гидравлической энергии обеспечивает гидравлической энергией все модули, которым она может потребоваться, такая энергия может передаваться по гидравлической шине. Зондирующие модули, которые могут иметь один или несколько зондов, включают в себя поршни для зацепления зонда (зондов) с сообщением по флюиду с пластами. Модули отбора проб содержат отборные камеры для сбора проб пластовых флюидов и могут быть соединены с местами отбора непосредственно или посредством сборной линии. Откачивающий модуль может быть использован для удаления нежелательных флюидов. В модуле анализатора использован оптический анализ для идентификации определенных характеристик флюидов. Методики анализа флюидов описаны, например, в патенте США №6178815 (Felling et al.) и/или в документе U4994671 (Safinya et al.). Кроме того, предусмотрена возможность измерения температуры и давления. Пакерный модуль включает в себя надувные пакерные элементы, которыми можно уплотнять периметр скважины по всей длине пакерных элементов. Используя вышеупомянутые модули и модули других типов, можно сконфигурировать прибор для выполнения разнообразных функций.

Скважинное устройство представляет собой спускаемое на кабеле устройство. Однако могут быть использованы разнообразные скважинные приборы. Например, могут быть использованы скважинный буровой инструмент, гибкая колонна, испытатель пласта, спускаемый на бурильной колонне, или другие приборы, пригодные для извлечения флюида.

В настоящем изобретении используются ядерно-магнитные резонансные измерения в сборной линии, и они могут быть выполнены посредством оборудования такого типа, как раскрыто в патенте США №6346813. Флюид, извлекаемый из пласта, протекает по каналу 221 (фиг.2). Канал сформирован толстостенной металлической трубой 224, способной противостоять пластовому давлению. На участке линии, снабженном устройством для ядерно-магнитных резонансных измерений, канал ограничен внутренним диаметром держателя 222 антенны. Держатель антенны изготовлен из непроводящего немагнитного материала, например из керамики или из твердого полимерного материала. Хотя на фиг.1 представлено устройство для измерений ядерно-магнитного резонанса, но могут быть выполнены разнообразные измерения, например оптические, в ближней инфракрасной области, инфракрасные, акустические, ультразвуковые, рентгеновские, измерения удельного сопротивления, микроволновые и другие физические измерения или измерения других параметров.

Антенна 223 для измерений ядерно-магнитного резонанса заключена в держатель антенны и излучает магнитное поле на частоте Лармора. Обычно это излучаемое магнитное поле называют В₁. Антенна для измерений ядерно-магнитного резонанса выполнена в виде соленоидной катушки, которая создает осциллирующее магнитное поле, параллельное оси отводного канала. Держатель антенны охвачен расширенной частью толстостенной металлической трубы 224, так что канал 221 не блокируется. Труба 224 и держатель 222 антенны могут выдерживать высокое давление пластовых флюидов в отводном канале. Высокочастотные магнитные поля не могут проникать через металлы, поэтому антенна для ядерно-магнитных резонансных измерений помещена внутрь металлической трубы. С наружной стороны толстостенной металлической трубы размещена группа постоянных магнитов 225. Они создают постоянное магнитное поле, обычно называемое В₀, по существу перпендикулярное к полю В₁, создаваемому антенной. Вся ядерно-магнитная установка заключена в корпус 226 зонда, который может быть прикреплен к другим аналогичным корпусам в инструментальной колонне. Кроме того, для выполнения измерений градиента импульсного поля с целью определения коэффициента диффузии и других величин могут быть предусмотрены градиентные катушки (не показаны).

Измерения, выполненные посредством ядерно-магнитного оборудования, могут быть обработаны обычным образом для определения параметров, в том числе спиновой плотности (пропорциональной амплитуде ядерно-магнитного резонансного сигнала), времен Т₁ продольной релаксации и времен Т₂ поперечной релаксации и их распределений, а также коэффициентов диффузии и их распределений.

Ниже описаны некоторые из теоретических положений, использованные в изобретении. Рассмотрим задачу предсказания свойств флюида на основании базы данных обучающих примеров. Задача может быть представлена как нелинейная многомерная задача регрессии. При заданном множестве входных данных (где представляют собой m-мерные вещественные векторы) и множестве соответствующих выходных данных при i=1, 2,…,N, где N - число выборок из базы данных, функция определяется так, что

для каждой пары «входные данные - выходные данные», где - случайные ошибки измерений. Используя теорию интерполяции с помощью радиальной базисной функции (S.Haykin, Neural networks: A Comprehensive Foundation, Second Edition, Chapter 5), функцию F можно записать в следующем виде

,

где - множество нелинейных функций, называемых радиальными базисными функциями. Обозначение удвоенными вертикальными чертами означает норму, которой обычно является норма L₂. Входные данные в базе данных являются центрами радиальных базисных функций, а представляет собой множество весовых векторов, выбранных так, что уравнения регрессии в (1) удовлетворяются. Micchelli (“Interpolation of Scattered Data: Distance Matrices And Conditionally Positive Definite Functions”, Constructive Approximation, v. 2, pp.11-22, 1986) показал, что матрица (интерполяции размера N на N с элементами является положительно определенной для функции Гаусса и для обратной мультиквадратичной функции, так что уравнения регрессии имеют вполне определенное решение в виде, задаваемом уравнением (2). В приведенном ниже преобразовании нормированные многомерные радиальные базисные функции Гаусса использованы для иллюстрации способа и перезаписи уравнения (2) в виде

.

В уравнении (3) гауссовская ширина (σ_j) является параметром, который аналогично весовым векторам может быть определен путем минимизации функции стоимости. При практических применениях хорошие результаты часто получают, используя единственную ширину (σ) для радиальных базисных функций Гаусса. Точно так же иногда полезно выбирать подмножество из входных данных в базе данных так, чтобы данные были центрами радиальных базисных функций. Можно упомянуть S. Haykin, см. выше, который рассмотрел несколько способов разумного выбора центров и параметров ширины.

Интуитивное понимание того, каким образом уравнение (3) может быть использовано для предсказания точных выходных данных по входным данным, которых нет в обучающей базе данных, может быть достигнуто при рассмотрении регрессионной оценочной функции Nadaraya-Watson (см., например, S.Haykin, выше). Уравнение для регрессионной оценочной функции Nadaraya-Watson или отображающей функции имеет ту же самую форму, что и уравнение (3), но весовой вектор заменен выходными данными базы данных и используется единственный параметр ширины, то есть

Видно, что уравнение (4) удовлетворяет условиям регрессии в уравнении (1) при условии, что перекрытия функций Гаусса очень малы. В пределе, при очень большом значении σ, приближается к значению выборочного среднего из всех выходных данных. В пределе, при очень малом значении σ, приближается к выходному значению , соответствующему входному значению , которое близко к . Отметим, что оценочная функция представляет собой взвешенное среднее из наблюдений и оценок и поэтому ограничена наблюдаемыми выборочными значениями. Кроме того, регрессионную оценочную функцию Nadaraya-Watson можно получить, используя негауссовские функции (см., например, D.F. Sprecht, IEEE Trans. on Neural Networks, vol. 2, no. 6, Nov. 1991). Простой пример, который привел Sprecht, демонстрирует возможности интерполяции с помощью радиальной базисной функции даже в случае разреженной базы данных «входные данные - выходные данные». На фиг.3 показана интерполяция с помощью линейной пилообразной функции (сплошная линия), определенной на основании набора из пяти пар «входное значение - выходное значение» (обозначены треугольниками). Кружками обозначены предсказанные выходные значения (F(x)) при заданных входных значениях (x). На фиг.4 показана чувствительность к различным параметрам ширины.

Лучшее приближение, чем регрессионная оценочная функция Nadaraya-Watson, получается в случае, когда n-мерным весовым вектором , определяемым в результате минимизации функции стоимости, заменяют выходные векторы в уравнении (4). Функция стоимости имеет вид

Функция стоимости может быть минимизирована относительно как весов, так и параметра ширины. В качестве альтернативы минимизацию можно выполнить, используя различные фиксированные значения параметра ширины, при этом оптимальным значением является то, при котором получается минимальное значение функции стоимости. Очевидно, что для определения оптимальных значений центров, ширин и весов может быть использована более общая функция стоимости (см., например, Haykin, глава 5).

В соответствии с ее свойством интерполяция с помощью радиальной базисной функции может быть использована для предсказания более точных оценок вязкости по сравнению с существующими корреляциями. Но сначала будут проанализированы эмпирические корреляции, используемые в существующих способах (см., например, Freedman et al., выше). Существующие способы основаны на следующих эмпирических уравнениях для оценки вязкости (η):

и

.

Уравнениями (6) и (7) даются оценки вязкости по результатам магнитно-ядерных резонансных измерений распределений времен (Т₂) релаксации поперечной намагниченности и коэффициентов (D) диффузии соответственно. В уравнении (6) вместо Т₂ может быть использовано распределение времен (Т₁) релаксации продольной намагниченности. Т - температура в градусах Кельвина, а f(gor) в уравнении (6) представляет собой определенную эмпирически функцию соотношения газ/нефть. В обоих уравнениях оценка вязкости обратно пропорциональна логарифмическому среднему распределения. Поэтому в корреляциях не учитывается то, что формы распределений могут влиять на вязкость. Кроме того, эмпирические постоянные a и b находят из условия «наилучшего соответствия» по отношению к предполагаемой форме регрессии для уравнений. Эмпирические постоянные в этих уравнениях не являются универсально подходящими для всякой сырой нефти, и дисперсия этих постоянных может привести к значительным погрешностям оцениваемых вязкостей. Дополнительный недостаток этих корреляций заключается в том, что в них не учтен эффект давления.

Следует отметить, что исходя из теоретических соображений распределения коэффициента диффузии должны быть лучшими прогнозирующими параметрами по сравнению с распределениями времени релаксации. То есть отчасти это обусловлено тем, что коэффициент диффузии является мерой поступательного движения молекул, тогда как время релаксации является мерой вращательного движения. Кроме того, в сырой нефти из-за присутствия парамагнитных ионов, таких как никель и ванадий, измеряемое время релаксации может уменьшаться, и поэтому обуславливает переоценку вязкости в уравнении (6).

Предсказание вязкости по результатам измерений ядерно-магнитного резонанса путем использования интерполяции с помощью радиальной базисной функции может рассматриваться как конструирование нелинейного отображения из векторной входной величины (например, из амплитуд в распределении Т₁ и Т₂ или D) в скалярную выходную величину (вязкость), определяемую набором примеров «входная величина - выходная величина». В нижеследующем примере распределения Т₂ использованы для иллюстрации методики, хотя понятно, что аналогичная методика может быть использована для распределений D и Т₁. Рассмотрим базу данных, состоящую из пар «входная величина - выходная величина», где входные величины для каждой пробы нефти включает в себя амплитуды распределения Т₂, температуры (T_i), давления (P_i) и соотношения (gor_i) газ/нефть, и из соответствующих выходных величин вязкости (η_i). Вязкость для пробы сырой нефти, отсутствующую в базе данных, можно предсказать, используя уравнение

Вязкость подвижной сырой нефти можно предсказать, используя уравнение (8) и измеренные амплитуды распределения Т₂, температуру (Т), давление (Р), соотношение (gor) нефть/газ. Соотношение нефть/газ можно также предсказать при условии, что имеется база данных результатов измерений, в которой gor присутствует в качестве выходной величины. Скважинный прибор для отбора проб флюида, снабженный датчиками давления и температуры и датчиком ядерно-магнитного резонанса (фиг.1), обеспечивает возможность выполнения измерений, необходимых для предсказания вязкости путем использования уравнения (8). В этом примере может быть получено соотношение газ/нефть, поскольку пробоотборник также снабжен оптическим анализатором флюидов, предназначенным для измерения оптической плотности сырой нефти в зависимости от длины волны в ближней инфракрасной области. Точность предсказаний, выполняемых с помощью уравнения (8), основана на наличии базы данных с хорошо подготовленным входным пространством данных измерений подвижной нефти. Величины веса и ширины в уравнении (8) можно определить на основании минимизации функции стоимости. Отметим, что в уравнении (8) представлены только амплитуды распределения Т₂, но не времена релаксации. Уравнение не зависит от амплитуд при условии, что все амплитуды в уравнении перекрывают один и тот же диапазон значений Т₂ (например, от 0,1 до 10000 мс).

Уравнение (8) легко обобщить, если в базу данных также включить результаты других измерений. Например, если в дополнение к амплитудам распределения Т₂ база данных включает в себя распределения D и Т₁, то в уравнении (8) амплитудные векторы для этих измерений будут присутствовать в виде дополнительных гауссовских множителей.

На фиг.5 показана схема последовательности операций, выполняемых процессором или процессорами, находящимися наверху и/или в скважине при управлении процессом, согласно варианту осуществления изобретения. Некоторые этапы должны быть выполнены заранее дистанционно от места расположения скважины.

На шаге 510 получают базу данных из результатов измерений «входных величин - выходных величин» ; пример процедуры для получения этой базы данных описан более подробно для последовательности операций на фиг.6А и 6В. На фиг.6А и 6В отражено, что измерения выполняют предпочтительно на пробах сырой нефти, а значения измерений сохраняют в базе данных в сочетании с условиями измерений. Обычно, хотя и не обязательно, измерения должны выполняться в так называемой «лаборатории измерения давления, объема и температуры». База данных может укомплектовываться и дополняться в течение значительного периода времени, чтобы объем данных, содержащихся в ней, возрастал.

В настоящем примере каждую пробу нефти измеряют в лаборатории при нескольких сочетаниях различных температур и давлений, и измерения включают в себя, например, ядерно-магнитные резонансные и оптические, а вязкость является «выходным» свойством флюида. Однако могут быть выполнены различные другие измерения (например, ультразвуковые, рентгеновские, измерения удельного сопротивления, оптические, в ближней инфракрасной области, инфракрасные, акустические, ультразвуковые, микроволновые и т.д.) в сочетании с дополнительными собранными «выходными» свойствами флюида (например, в сочетании с составом, определенным с помощью газовой хроматографии, давлением насыщения, коэффициентом пластового объема нефти, композицией из предельных углеводородов, ароматических соединений, смолистых веществ и асфальтенов и т.д.). На шаге 605 (фиг.6) осуществляют испытания первой пробы, а на шагах 610 и 615 задают соответственно первую температуру и первое давление при испытании. Затем на шагах 620, 625, 630 и 635 выполняют измерение текущей пробы при текущем давлении и температуре и сохраняют данные. На шаге 620 выполняют оптическое измерение, например, измерение оптической плотности, а на шаге 625 выполняют измерения ядерно-магнитного резонанса, которые могут быть обработаны для получения распределений Т₁, Т₂ и/или D. На шаге 630 выполняют измерения вязкости. На шаге 635 сохраняют значения вязкости в базе данных (в качестве «выходного» значения) в сочетании с результатами измерений ядерно-магнитного резонанса, значениями оптической плотности и текущими значениями давления и температуры. Ставится вопрос на шаге 640 принятия решения о том, будет ли учитываться последняя температура. Если нет, то задается на шаге 648 следующая температура и выполняются измерения, результаты сохраняются, а цикл 647 повторяется до тех пор, пока все температуры в заданном диапазоне не будут учтены. Затем ставится вопрос на шаге 650 принятия решения о том, будет ли учитываться последнее давление. Если нет, то задается на шаге 655 следующее давление, повторно устанавливается на шаге 657 температура, и цикл 659 (вместе с дополнительным циклом 647) повторяется до тех пор, пока не будут задействованы все сочетания давлений и температур в заданных диапазонах. Затем ставится вопрос на шаге 660 принятия решения о том, будет ли испытываться последняя проба. Если нет, то для испытания выбирается (шаг 670) следующая проба, при этом происходит повторное обращение к шагу 610, и цикл 665 продолжается до тех пор, пока все пробы не будут испытаны, а фаза формирования базы данных не завершится.

Используя базу данных (фиг.5), конструируют (шаг 520) отображающую функцию радиальной базисной функции в соответствии с уравнением (3). Затем, используя и , в соответствии с уравнением (5) конструируют (шаг 525) функцию стоимости. Функцию стоимости минимизируют (шаг 530), чтобы определить оптимальные параметры, такие как веса и ширины.

На шаге 540 размещают устройство 100 для испытания пласта в скважине на отметке глубины, представляющей интерес (например, в зоне вероятного содержания углеводородов), а на шаге 545 устанавливают устройство на заданном месте и извлекают пластовый флюид в сборную линию. Как известно в области техники, до извлечения испытуемого флюида может быть осуществлено предварительное испытание.

На шагах 551, 552 и 553 выполняют измерения на флюидах, извлекаемых в устройство для испытания пласта. В частности, на шаге 551 измеряют температуру и давление, на шаге 552 измеряют ядерно-магнитный резонанс, например, путем использования установки для измерений ядерно-магнитного резонанса со сборной линией (фиг.2), а на шаге 552 выполняют оптические измерения, например, посредством описанного выше оптического анализатора флюидов. На шаге 560 осуществляют обработку известным способом результатов ядерно-магнитных резонансных измерений для получения распределений Т₂, Т₂ и/или D (коэффициентов диффузии). На шаге 570 осуществляют обработку известным способом оптических данных для получения соотношения (gor) газ/нефть. Затем на шаге 580 на основании определяют свойство флюида (в этом примере вязкость). В этом примере уравнение (8) применяют для определения вязкости в зависимости от амплитуд распределения Т₂, температуры, давления и соотношения газ/нефть, используя базу данных и найденные оптимальные параметры весов и ширин. При желании процесс можно повторить (шаг 590), например, для других отметок глубины, чтобы получить каротажную диаграмму определяемого свойства.

Чтобы проиллюстрировать предсказание вязкости на простом примере, в котором используются искусственные данные, рассмотрим обучающую базу данных «входная величина - выходная величина», состоящую из входных величин, которые представляют собой распределения Т₂ с гауссовской формой. Они соответствуют в уравнении (8). Выходными величинами обучающей базы данных являются вязкости (η_i), вычисленные по логарифмическому среднему путем использования уравнения (6). В этом примере нефть представляет собой дегазированную нефть, для которой gor=0, а функция f(gor) в уравнении (3) равна единице. Для проверки предсказания вязкости был использован контрольный (то есть тестовый) набор искусственных распределений Т₂ с гауссовской формой. Обучающие и тестовые распределения показаны на фиг.7, причем обучающие и тестовые данные имеют различные формы (различные положения и ширину). Предполагается, что обучающие и тестовые данные получены для одних и тех же значений температуры и давления.

На фиг.8 показана вязкость, предсказанная для каждого тестового распределения путем использования уравнения (8), в сопоставлении с истинной вязкостью, вычисленной на основании уравнения (6).

Кроме того, способ предсказания вязкости путем использования амплитуд распределения Т₂ может быть непосредственно применен к распределениям D или Т₁. База данных из распределений D или Т₁ и соответствующие измеренные вязкости должны быть использованы для конструирования уравнений, аналогичных уравнению (8).

Предсказанные значения вязкости были также проверены путем использования базы данных из распределений Т₂ и соответствующих измеренных вязкостей, полученных для набора 16 проб дегазированной пластовой нефти при температуре 30°С и атмосферном давлении. Измеренные значения вязкости приведены в таблице 1. Соответствующие измеренные распределения Т₂ показаны на фиг.9А-Р.

Таблица 1Измеренные значения вязкости для 16 проб дегазированной пластовой нефти
Проба	Измеренная вязкость (сП)
1	6,30
2	13,9
3	16,4
4	746,0
5	5,09
6	6,36
7	6,52
8	656,0
9	5,42
10	8,47
11	980,0
12	15,5
13	8,46
14	116,0
15	132,0
16	91,2

Отметим, что пробы 10 и 13 имеют почти идентичные измеренные вязкости, но их распределения Т₂ имеют совершенно различные логарифмические средние. Например, для пробы 10 среднее значение составляет 174 мс, тогда как для пробы 13 среднее значение составляет 279 мс. Посредством этих двух проб выявляется очевидный недостаток способа из уровня техники (уравнение (6)) относительно предсказания вязкости нефти на основании измерений распределений Т₂ при ядерно-магнитном резонансе. На фиг.10 показано предсказание вязкости по радиальной базисной функции. Вязкость каждой пробы была предсказана путем использования базы данных, сод