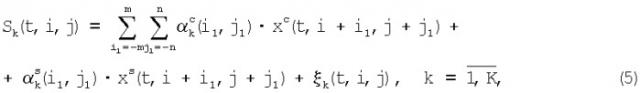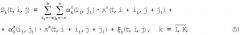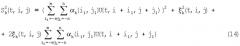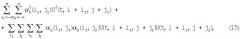Способ формирования изображений в многоканальных ртлс и рлс

Способ формирования изображений в многоканальных ртлс и рлс

Иллюстрации

Показать все

Реферат

Изобретение относится к пассивной и активной радиолокации, а именно к радиотеплолокационным и радиолокационным станциям (РТЛС, РЛС) наблюдения за наземными и воздушными объектами на базе подвижных или неподвижных носителей станций с антенными решетками (многолучевыми, многосенсорными антенными системами) [1], [2, с.9-11].

При наблюдении РТЛС или РЛС за наземной или воздушной обстановкой осуществляется построчное сканирование антенной зоны обзора с непрерывным смещением линии визирования антенны по азимуту и углу места [1, с.71-73], [2-5]. При этом формируется двумерное радиоизображение наземных или воздушных объектов на фоне окружающей обстановки. Четкость изображения и точность определения угловых координат объектов при таком способе формирования изображения ограничена шириной диаграммы направленности антенны (ДНА). Возникает проблема повышения разрешающей способности РТЛС или РЛС по углам за счет алгоритмической обработки полученного изображения. Известны способы повышения разрешающей способности по угловым координатам сканирующих РЛС в режиме "реального луча" [4, 5], которые могут быть использованы также для повышения разрешающей способности сканирующих РТЛС. Однако эти способы обладают недостатками - потерей информации об изображении по периметру зоны обзора и ограниченной точностью восстановления изображений из-за малого числа измерительных каналов.

Наиболее близким по технической сущности является способ повышения разрешающей способности по угловым координатам [5], который заключается в восстановлении матрицы изображения в заданном диапазоне дальности и сводится к следующим операциям.

1. Линию визирования антенны РЛС последовательно смещают по азимуту и углу места соответственно на величину (2n+1)-й и (2m+1)-й части ширины ДНА построчно в зоне обзора. Ширина ДНА на уровне 0,5 мощности в осевом сечении составляет 2n+1 элементов дискретизации по азимуту и 2m+1 элементов дискретизации по углу места.

2. Полученные при каждом i,j-м положении луча амплитуды отраженных сигналов на выходе первого канала y₁(i,j) помещают в матрицу измерений Y₁ с элементами y₁(i,j), , , а амплитуды на выходе второго канала y₂(i,j) помещают в матрицу измерений Y₂ с элементами y₂(ij), , .

3. Относительно каждого i,j-го элемента x(i,j), , искомой матрицы изображения Х строится плавающее окно ограниченного размера (2m₁+1)×(2n₁+1), m₁>m, n₁>n. Амплитуды y_k(i+i₁,j+j₁), k=1, 2, взятые в этом окне при , , суммируют по i₁ и j₁ с весовыми коэффициентами h_k(i₁,j₁), k=1, 2, расчет которых осуществляют заранее по методу наименьших квадратов (МНК). В результате получают оценку

искомого изображения в центральном элементе окна для числа каналов К=2.

4. Полученные по совокупности i,j-x положений луча оценки , , располагают в составе (I-2m₁)×(J-2n₁) - матрицы , которая представляет восстановленное изображение в i,j-x синтезированных элементах разрешения по азимуту и углу места.

Однако такой способ обладает следующими недостатками.

1. В полученной (I-2m₁)×(J-2n₁) - матрице оценок с элементами , , теряется информация об изображении по периметру зоны обзора, и искомая I×J - матрица с элементами , , оказывается полностью незаполненной. Это вызвано тем, что в плавающем окне вычисляется только одна оценка, соответствующая центру окна.

2. Расширение множества оценок до зоны обзора требует дополнительного сканирования, что снижает быстродействие системы наблюдения.

3. Расчет весовых коэффициентов h_k(i₁,j₁) для формулы (1) дан для антенной системы, приемные элементы которой принимают один и тот же сигнал в одной фазе, и не предусматривает общего случая, когда приемные элементы многоканальной антенны, размещенные в виде антенной решетки, принимают сигнал в разных фазах.

Устранение указанных недостатков требует изменения способа обработки результатов измерения.

Технический результат направлен на расширение области четкого видения до области обзора РТЛС и РЛС, а также повышение точности восстановления изображения.

Технический результат предлагаемого технического решения достигается тем, что способ формирования изображений в многоканальных радиотеплолокационных и радиолокационных станциях заключается в том, что при наблюдении за поверхностью или воздушной обстановкой с помощью сканирующей К-канальной антенны в виде решетки приемных элементов последовательно смещают линию визирования антенны по азимуту и углу места соответственно на величину (2n+1)-й и (2m+1)-й части ширины диаграммы направленности антенны на уровне 0,5 мощности построчно в зоне обзора, где n и m - элементы дискретизации соответственно по азимуту и углу места, измеряют при каждом i,j-м положении антенны в k-x измерительных каналах значения приемных сигналов и формируют из них I×J - матрицы измерений Y_k с элементами y_k(i,j), , , , которые далее обрабатывают, отличающийся тем, что при обработке данных используют полное окно, соответствующее размеру области сканирования I×J, увеличивают число каналов измерения К, сворачивают полученные матрицы измерений Y₁, Y₂, …, Y_K в один IJK-вектор измерений , который умножают справа на (I+2m)(J+2n)×IJK - матрицу весовых коэффициентов Н, вычисляемую заранее, тем самым получают (I+2m)(J+2n) - вектор оценок , затем разворачивают вектор построчно в (I+2m)×(J+2n) - матрицу X, представляющую восстановленное изображение в расширенной зоне обзора с разрешением по угловым координатам.

Способ осуществляется следующим образом.

1. Антенная система, представляющая собой антенную решетку, построчно сканирует в зоне обзора, смещаясь по азимуту и углу места непрерывно, а измерения осуществляются с малым шагом дискретизации.

2. Цифровая система обработки принимаемых сигналов измеряет в каждом k-м канале (k=1, 2, …, К) независимо сигналы в дискретные моменты времени, совпадающие с j,1-ми шагами дискретизации по углам, составляющими (2n+1)-ю и (2m+1)-ю часть ширины ДНА на уровне 0,5 мощности по азимуту и углу места, и формирует из них I×J - матрицы измерений каналов Y₁, Y₂, …, Y_K.

3. Полученные матрицы измерений Y₁, Y₂, …, Y_K последовательно сворачиваются в один IJK-вектор измерений .

4. Вектор умножается справа на (I+2m)(J+2n)×IJK - матрицу весовых коэффициентов Н, вычисляемую заранее по методике, представленной в расчетной части заявки, тем самым получается (I+2m)(J+2n) - вектор оценок .

5. Вектор оценок разворачивается построчно в (I+2m)×(I+2n) - матрицу X, представляющую восстановленное изображение в расширенной зоне обзора с повышенным в несколько раз разрешением по угловым координатам.

Расчет матриц весовых коэффициентов для многоканальной РТЛС без амплитудного детектирования сводится к следующему.

Дискретная модель измерений при i,j-м фиксированном положении антенны по углу места (по i) и азимуту (по j) на входе цифровой системы обработки приемного сигнала описывается следующей суммарной зависимостью:

где S_k(t,i,j) - принимаемый сигнал в k-м канале (); α_k(i,j) - нормированные коэффициенты ДНА k-го канала, характеризующие интенсивность прихода сигнала с i,j-го углового направления в k-м приемном элементе антенны; U(t,i,j) - полезная i,j-я составляющая сигнала, несущая информацию о поле излучения в i,j-м направлении, причем амплитуда A(t,i,j) и начальная фаза φ(t,i,j) - случайные функции времени t и пространственных координат i,j; круговая частота ω₀=2πf₀ соответствует центру полосы частот, в которой принимается сигнал [1]. Закон распределения A(t,i,j) во времени t при фиксированных i,j близок к нормальному: . Начальная фаза φ(t,i,j) по t, i, j распределена равномерно на [0,2π]; γ_k{i,j) - известное запаздывание сигнала по фазе при приеме сигнала с i,j-го направления в k-м элементе антенны, где значение γ_k(i,j)=0 принимается для центра антенной системы; ξ_q(t) - гауссовский белый шум: . Размер ДНА на уровне 0,5 мощности в осевом сечении составляет 2n+1 элементов дискретизации по азимуту и 2m+1 элементов дискретизации по углу места.

Представим (3), опустив символы t, i, j и обозначив ψ(t,i,j)=ω₀t-φ(t,i,j):

С учетом (4) модель измерений (2) принимает вид

где

- косинусная и синусная составляющие коэффициентов ДНА, зависящие от известной фазы γ_k(i,j) запаздывания сигнала по приемным элементам;

- косинусная и синусная составляющие полезного сигнала, зависящие от случайной функции ψ(t,i,j), причем

Задача с позиции модели (5) заключается в поиске наилучших в определенном смысле оценок полезных составляющих (7): x^s, x^c с оцениванием амплитуды А по формуле (8) для фиксированного момента времени t.

Для решения этой задачи в каждый дискретный момент времени t_µ, соответствующий i,j-му положению антенны, выполняются следующие построения.

1. Измерения S_k всех k-x каналов () последовательно размещаются в К-векторе .

2. Искомые параметры (7) парами x^s, x^c последовательно (в соответствии с нумерацией i,j) располагаются в 2(2m+1)(2n+1) - векторе .

3. Коэффициенты ДНА (6) располагаются построчно парами , в составе К×2(2m+1)(2n+1)-матрицы А: вначале для 1-го канала, затем 2-го и т.д. К-го.

4. Помехи ξ_k находятся в К-векторе .

5. Построения п.п. 2-4 отражают структуру вектора , матрицы А, вектора и не входят в операции обработки данных. Возможна иная организация размещения элементов в векторах , , и матрице А.

При таких построениях модель измерений (2) принимает вид матрично-векторного уравнения относительно неизвестного вектора :

Оптимальные оценки вектора при отсутствии статистической информации относительно и находятся по критерию минимума квадрата нормы (или МНК):

где Т - символ транспонирования.

Решение (10) дает стандартные МНК-оценки:

где δ - параметр регуляризации, необходимый для обращения матрицы A^Т А в случае ее плохой обусловленности (например, [6, с.55]); Е - единичная матрица; Н₁ - матрица весовых коэффициентов.

Точность оценок (11) при δ→0 и некоррелированных помехах характеризуется корреляционной матрицей R_ΔX ошибок оценивания .

и определяется дисперсией помех и структурой матрицы А, зависящей от формы ДНА.

При числе измерений большем, чем число неизвестных параметров: К>2(2m+1)(2n+1), дисперсии оценок параметров (диагональные элементы матрицы R_ΔX) меньше дисперсии помех , чем достигается необходимая разрешающая способность, зависящая от точности оценивания.

Элементы вектора оценок , взятые последовательно парами x^s, x^c, возводятся в квадрат, суммируются и из полученного значения извлекается корень согласно (8), что приводит к оценкам амплитуд

которые построчно располагаются в составе (2m+1)×(2n+1)-матрицы X(i,j) с элементами x(i₁,j₁), , . Матрица X(i,j) представляет восстановленное в пределах ширины ДНА при i,j-м положении антенны амплитудное изображение наземной или воздушной обстановки с повышенной в несколько раз разрешающей способностью по углам.

Предложенная процедура оценивания позволяет значительно уменьшить время обработки по сравнению с традиционными методами [1], основанными на детектировании результатов измерения РТЛС и последующем осреднении с помощью фильтра низких частот.

В случае традиционного метода измерения в РТЛС, основанного на детектировании и осреднении, модель измерений и соответствующий алгоритм обработки сводятся к следующему. В соответствии со схемой простейшего радиометра [1] сигнал (2), (3) подается на вход квадратичного детектора, на выходе которого - квадратичная функция входного сигнала:

где квадрат суммы раскладывается на составляющие:

и вторая сумма берется по всем несовпадающим i₁, i₂, j₁, j₂ (i₁≠i₂, j₁≠j₂).

Так как в (3) начальная фаза φ(t,i,j) случайным образом принимает значения на [0,2π], то U(t,i,j) - центрированная случайная функция t (с нулевым математическим ожиданием).

После детектора сигнал (14) подается на вход фильтра низких частот (ФНЧ), который усредняет во времени t. При усреднении произведения некоррелированных центрированных случайных величин дают близкие к нулевым средние значения. В результате на выходе ФНЧ действует следующая модель:

где P_k(i,j) - ошибка усреднения, которую можно принять гауссовской: , причем σ_P>σ_ξ (или даже σ_P>>σ_ξ в зависимости от свойств полей излучения). Для стационарного центрированного процесса ξ_k(t) его средний квадрат равен дисперсии: .

При усреднении U(t,i,j), определенного моделью (3), учтем, что среднее значение квадрата случайной амплитуды A(t,i,j) равно сумме квадрата ее среднего значения и дисперсии, а среднее значение квадрата косинуса на промежутке [0,2π] равно 1/2. Получим

Далее обозначим - измерения; - параметры поля излучения, подлежащие оцениванию. Понимая под α_k(i,j) квадрат коэффициента ДНА , получим окончательно дискретную модель измерения y_q(i,j) для сигнала на выходе ФНЧ радиометра, необходимую для дальнейшей алгоритмической обработки:

Точность восстановления зависит от величины отношения сигнал-шум по мощности в (18), которая меньше, чем в модели (5), так как σ_P>σ_ξ.

Задача с позиции модели (18) заключается в восстановлении (оценивании) параметров x(i,j) поля излучения U(i,j) и формировании I×J-матрицы изображения x(i,j), , на основе измерений (18), полученных на множестве i,j-x положений антенны.

Для решения этой задачи выполняются следующие построения.

1. Измерения y_k(i,j), , , всех k-x каналов () последовательно размещаются в IJK-векторе : построчно считываются измерения 1-го канала, затем 2-го и т.д. К-го.

2. Искомые параметры x(i,j) построчно располагаются в (I+2m)(J+2n) - векторе .

3. Коэффициенты ДНА α_k(i,j) располагаются построчно в составе IJK×(I+2m)(J+2n) - матрицы А: вначале для 1-го канала, затем второго и т.д. К-го.

4. Помехи p_k(i,j) находятся в IJK-векторе .

5. Построения п.п.п. 2-4 отражают структуру данных. Возможна иная организация размещения элементов в векторах , , и матрице А.

Модель измерений (18) принимает вид векторно-матричного уравнения относительно неизвестного вектора X:

Оптимальные оценки вектора находятся по критерию (10):

Точность оценок (20) при δ→0 и некоррелированных помехах характеризуется корреляционной матрицей:

При числе измерений, большем, чем число неизвестных параметров: IJK>(I+2m)(J+2n), дисперсии оценок (диагональные элементы матрицы R_ΔX) меньше дисперсии помех .

Вектор построчно разворачивается в матрицу X, которая представляет восстановленное амплитудное изображение наземной или воздушной обстановки в зоне обзора РТЛС с повышенной в несколько раз разрешающей способностью по углам.

Расчет матриц весовых коэффициентов для РЛС сводится к следующему.

При i,j-м положении антенны модель комплексной огибающей отраженного сигнала, отселектированного на промежутке времени [t,t+Δt], соответствующем заданному диапазону дальности (в частном случае - элементу разрешения дальности), и прошедшего тракт первичной обработки, на выходе фильтров низких частот квадратурных каналов фазового детектирования k-го приемного канала имеет вид (например, [7, с.13-14]):

Здесь: - сигнал в квадратурных каналах фазового детектирования с измеряемой амплитудой S_k(t,i,j) и измеряемой фазой φ_k(t,i,j), где множитель i обозначает мнимую единицу; - нормированные комплексные коэффициенты ДНА k-го канала; - полезная составляющая сигнала со случайной амплитудой A(t,i,j), несущей информацию о поле отражения, и случайной равномерно на [0,2π] фазой ψ_k(t,i,j); γ_k(i,j) - известный фазовый сдвиг при приеме отраженного сигнала с i,j-го углового направления k-м приемным элементом по сравнению с центром антенной системы; - комплексный гауссовский белый шум, действительная и мнимая составляющие которого распределены по нормальному закону с нулевым математическим ожиданием и дисперсией .

Представим (22) в виде

где

- комплексный сигнал, подлежащий оцениванию, модулем которого является амплитуда сигнала отражения A(t,i,j).

Модель измерения (23) аналогично (9) или (19) представляется в векторно-матричной форме:

где - IJK-вектор комплексных измерений (23), взятых по совокупности i,j,k; - IJK×(1+2m)(J+2n) - матрица комплексных коэффициентов ДНА; - (I+2m)(J+2n) - вектор комплексных оцениваемых параметров; - IJK-вектор комплексных ошибок измерения.

Оптимальные МНК-оценки вектора находятся по критерию, аналогичному (10):

где *Т - символ комплексного сопряжения и транспонирования, и принимают вид

где - матрица комплексных весовых коэффициентов; - комплексный параметр регуляризации.

Точность оценивания (24) при и некоррелированных помехах характеризуется комплексной корреляционной матрицей ошибок оценивания :

В качестве оценок амплитуд поля отражения берутся модули элементов вектора , которые построчно размещаются в матрице восстановленного изображения X.

Если после когерентного накопления комплексный сигнал (23) детектируется по амплитуде (берется его модуль или квадрат модуля), а продетектированные сигналы некогерентно накапливаются (усредняются) для повышения отношения сигнал-шум и борьбы со спекл-искажениями, то получается действительная модель вида (16), (18), (19) и оценки (20). Однако за счет нелинейных преобразований уровень помех в (16), (18) может быть значительно выше, чем в линейных моделях (2), (22): σ_P>σ_ξ.

Предлагаемый способ позволяет в несколько раз повысить разрешающую способность РТЛС и РЛС по азимуту и углу места с сохранением области обзора при наблюдении за наземными и воздушными объектами.

Литература

1. Николаев А.Г., Перцов С.В. Радиотеплолокация. М.: Воен. изд-во., 1970. 132 с.

2. Пирогов Ю.А. Пассивное радиовидение в миллиметровом диапазоне // Радиотехника. 2003. №2. С.4-11.

3. Пирогов Ю.А., Тимановский А.Л. Сверхразрешение в системах пассивного радиовидения миллиметрового диапазона // Радиотехника. 2006 № 3. С.14-19.

4. Патент RU 2284548 C1. Способ наблюдения за поверхностью и воздушной обстановкой на базе бортовой РЛС / В.К.Клочко. МПК: G01S 13/02. Приоритет 23.06.2005. Опубл.: 27.09.2006. Бюл. № 27.

5. Патент RU 2292060 C1. Способ наблюдения за воздушными объектами и поверхностью на базе бортовой РЛС / В.К.Клочко. МПК: G01S 13/02. Приоритет 28.06.2005. Опубл.: 20.01.2007. Бюл. № 2.

6. Василенко Г.И., Тараторин A.M. Восстановление изображений. М.: Радио и связь, 1986. 304 с.

7. Радиолокационные станции с цифровым синтезированием апертуры антенны / В.Н.Антипов, В.Т.Горяинов, А.Н.Кулин, Толстов Е.Ф. и др. Под ред. В.Т.Горяинова. М.: Радио и связь, 1988. 304 с.

Способ формирования изображений в многоканальных радиотеплолокационных и радиолокационных станциях, заключающийся в том, что при наблюдении за поверхностью или воздушной обстановкой с помощью сканирующей К-канальной антенны в виде решетки приемных элементов последовательно смещают линию визирования антенны по азимуту и углу места соответственно на величину (2n+1)-й и (2m+1)-й части ширины диаграммы направленности антенны на уровне 0,5 мощности построчно в зоне обзора, где n и m - элементы дискретизации соответственно по азимуту и углу места, измеряют при каждом i,j-м положении антенны в k-x измерительных каналах значения амплитуд приемных сигналов и формируют из них I×J-матрицы измерений Y_k с элементами y_k(ij), , , , которые далее обрабатывают, отличающийся тем, что при обработке данных используют полное окно, соответствующее размеру области сканирования I×J, увеличивают число каналов измерения К, сворачивают полученные матрицы измерений Y₁, Y₂, …, Y_K в один IJK-вектор измерений , который умножают справа на (I+2m)(J+2n)·IJK-матрицу весовых коэффициентов Н, вычисляемую заранее, тем самым получают (I+2m)(J+2n) - вектор оценок , затем разворачивают вектор построчно в (I+2m)·(J+2n)-матрицу X, представляющую восстановленное изображение в расширенной зоне обзора с повышенным в несколько раз разрешением по угловым координатам.