Устройство и способ кодирования-декодирования блочного кода проверки на четность с низкой плотностью с переменной длиной блока

Устройство и способ кодирования-декодирования блочного кода проверки на четность с низкой плотностью с переменной длиной блока

Иллюстрации

Показать все

Реферат

Область техники, к которой относится изобретение

Настоящее изобретение, в общем, относится к системе мобильной связи, и в частности к устройству и способу кодирования/декодирования блочных кодов проверки на четность с низкой плотностью (LDPC, ПЧНП).

Уровень техники

В результате быстрого развития систем мобильной связи возникла необходимость разработки технологии, позволяющей передавать большие массивы данных, приближаясь к пропускной способности кабельной сети в беспроводной среде связи. Для удовлетворения все увеличивающейся потребности в высокоскоростной системе связи, работающей с высокой пропускной способностью, которая позволяет обрабатывать и передавать различные данные, такие как данные изображения и радиоданные, помимо услуги, ориентированной на голосовую передачу, требуется повысить эффективность передачи системы, используя соответствующую схему кодирования канала, чтобы, таким образом, улучшить общие рабочие характеристики системы. Однако мобильная система связи, с учетом ее характеристик, неизбежно генерирует ошибки во время передачи данных из-за шумов, помех и затухания, в соответствии с условиями канала. Генерирование ошибок приводит к потере большого количества информационных данных.

Для предотвращения потери информационных данных в результате генерирования ошибок в настоящее время используют различные схемы управления ошибками, которые частично основаны на характеристиках канала, чтобы, таким образом, повысить надежность системы мобильной связи. В наиболее типичной схеме управления ошибками используют коды коррекции ошибок.

Ниже, со ссылкой на фиг. 1, приведено описание структуры передатчика/приемника в общей системе мобильной связи.

На фиг. 1 показана схема, иллюстрирующая структуру передатчика/приемника в общей системе мобильной связи. Как показано на фиг. 1, передатчик 100 включает в себя кодер 111, модулятор 113 и радиочастотный (RF, РЧ) процессор 115, и приемник 150 включает в себя РЧ процессор 151, демодулятор 153 и декодер 155.

В передатчике 100, если генерируют информационные данные "u", предназначенные для передачи, их передают в кодер 111. Кодер 111 генерирует кодированный символ "c" путем кодирования информационных данных "u", используя заданную схему кодирования, и выводит кодированный символ "c" в модулятор 113. Модулятор 113 генерирует символ "s" модуляции в результате модуляции кодированного символа "c" использованием заданной схемы модуляции и выводит символ "s" модуляции в РЧ процессор 115. РЧ процессор 115 выполняет РЧ обработку символа модуляции "s", поступающего с выхода модулятора 113, и передает сигнал после РЧ обработки по беспроводному каналу связи через антенну ANT (АНТ).

Сигнал, переданный по беспроводному каналу связи передатчиком 100, таким образом, принимают в приемнике 150 через его антенну АНТ, и сигнал, принятый через антенну, подают в РЧ процессор 151. РЧ процессор 151 выполняет РЧ обработку принятого сигнала и выводит сигнал "r" после РЧ обработки в демодулятор 153. Демодулятор 153 демодулирует сигнал "r" после РЧ обработки, поступающий с выхода РЧ процессора 151, используя схему демодуляции, соответствующую схеме модуляции, использованной в модуляторе 113, и выводит демодулированный сигнал "x" в декодер 155. Декодер 155 декодирует демодулированный сигнал "x", поступающий с выхода демодулятора 153, используя схему декодирования, соответствующую схеме кодирования, использованной в кодере 111, и выводит декодированный сигнал "u" в качестве окончательно декодированных информационных данных.

Для обеспечения возможности декодирования без ошибок в приемнике 150 информационных данных "u", переданных передатчиком 100, необходимо использовать высокоэффективный кодер и декодер. В частности, поскольку требуется учитывать среду радиоканала и характеристики мобильной системы связи, следует более серьезно учитывать ошибки, которые могут быть сгенерированы под влиянием среды радиоканала.

Наиболее типичные коды коррекции ошибки включают в себя турбокоды и коды проверки на четность с низкой плотностью (LDPC).

Известно, что турбокод обеспечивает лучшее повышение рабочих характеристик по сравнению со сверточным кодом, который обычно используют для коррекции ошибок во время передачи данных с высокой скоростью. Преимущество турбокода состоит в том, что он позволяет эффективно корректировать ошибку, вызванную шумами, генерируемыми в канале передачи данных, повышая, таким образом, надежность передачи данных. Код LDPC можно декодировать, используя итеративный алгоритм декодирования, основанный на алгоритме суммирования-умножения в фактор-графе. Поскольку в декодере для кода LDPC используют итеративный алгоритм декодирования на основе алгоритма суммирования-умножения, он является менее сложным, чем декодер для турбокода. Кроме того, декодер для кода LDPC легко воплотить на практике, используя декодер параллельной обработки, по сравнению с декодером для турбокода.

Теорема Шеннона кодирования канала показывает, что надежная связь возможна только при скорости передачи данных, не превышающей пропускную способность канала. Однако теорема Шеннона кодирования канала не предлагает подробный способ кодирования/декодирования канала для поддержания скорости передачи данных вплоть до максимальной предельной пропускной способности канала. Обычно, хотя случайный код, имеющий очень большой размер блока, проявляет рабочие характеристики, приближающиеся к предельному значению пропускной способности канала в соответствии с теоремой Шеннона кодирования канала, на практике, при использовании способа декодирования MAP (maximum a posteriori, МАВ (максимум апостериорной вероятности)) или ML (МП, максимального правдоподобия), невозможно выполнить этот способ декодирования из-за чрезвычайно большой вычислительной нагрузки.

Турбокод был предложен авторами Berrou, Glavieux и Thitimajshima в 1993 г., и он проявляет исключительные рабочие характеристики, которые приближаются к предельному значению пропускной способности канала в соответствии с теоремой Шеннона кодирования канала. Появление турбокода инициировало активное исследование в области итерационного декодирования и графического выражения кодов, в результате коды LDPC, предложенные автором Gallager в 1962 г., вышли на первый план в этих исследованиях. В фактор-графе турбокода и кода LDPC существуют циклы, и известно, что итерационное декодирование в фактор-графе кода LDPC, в котором существуют циклы, является субоптимальным. Кроме того, экспериментально было подтверждено, что код LDPC обладает исключительными характеристиками при использовании итеративного декодирования. Код LDPC, как известно, проявляет наилучшие характеристики, отличающиеся только приблизительно на 0,04 [дБ] от предельного значения пропускной способности канала, в соответствии с теоремой Шеннона кодирования канала, с частотой передачи ошибочных битов (BER, ЧБО) 10^-5, при использовании размера блока 10⁷. Кроме того, хотя сложность процесса декодирования кода LDPC, определенного в поле Галуа (GF, ПГ) при q > 2, то есть GF(q), увеличивается, его характеристики намного превышают двоичный код. При этом, однако, отсутствует удовлетворительное теоретическое описание успешного декодирования с использованием итеративного алгоритма декодирования для кода LDPC, определенного в GF(q).

Код LDPC, предложенный автором Gallager, определен по матрице проверки на четность, в которой большая часть элементов имеет значение 0 и меньшая часть элементов, за исключением элементов, имеющих значение 0, имеет ненулевое значение, например значение, равное 1. В следующем описании предполагается, что не равное нулю значение представляет собой значение, равное 1.

Например, код LDPC (N, j, k) представляет собой линейный блочный код, имеющий длину блока N, и определен как разреженная матрица проверки на четность, в которой каждый столбец имеет j элементов, имеющих значение 1, каждая строка имеет k элементов, имеющих значение 1, и все элементы, за исключением элементов, имеющих значение 1, имеют значение 0.

Код LDPC, в котором вес каждого столбца в матрице проверки на четность фиксирован значением "j" и вес каждой строки в матрице проверки на четность фиксирован значением "k", как описано выше, называется "регулярным кодом LDPC". Здесь "вес" относится к количеству элементов, имеющих ненулевое значение, среди элементов, составляющих матрицу проверки на четность. В отличие от регулярного кода LDPC, код LDPC, в котором не фиксированы вес каждого столбца и вес каждой строки в матрице проверки на четность, называется "нерегулярным кодом LDPC". Общеизвестно, что нерегулярный код LDPC обладает лучшими характеристиками по сравнению с регулярным кодом LDPC. Однако в случае нерегулярного кода LDPC, поскольку вес каждого столбца и вес каждой строки в матрице проверки на четность не фиксирован, то есть является нерегулярным, вес каждого столбца в матрице проверки на четность и вес каждой строки в матрице проверки на четность необходимо соответствующим образом регулировать для гарантирования лучших рабочих характеристик.

Ниже, со ссылкой на фиг. 2, приведено описание матрицы проверки на четность кода LDPC (8, 2, 4) в качестве примера кода LDPC (N, j, k).

На фиг. 2 показана схема, иллюстрирующая матрицу проверки на четность для общего кода LDPC (8, 2, 4). Как показано на фиг. 2, матрица H проверки на четность кода LDPC (8, 2, 4) состоит из 8 столбцов и 4 строк, в которой вес каждого столбца фиксирован и равен 2 и вес каждой строки фиксирован и равен 4. Поскольку вес каждого столбца и вес каждой строки в матрице проверки на четность является регулярным, как указано выше, код LDPC (8, 2, 4), представленный на фиг. 2, становится регулярным кодом LDPC.

Матрица проверки на четность кода LDPC (8, 2, 4) была описана выше со ссылкой на фиг. 2. Далее, со ссылкой на фиг. 3, будет описан фактор-граф кода LDPC (8, 2, 4), описанного со ссылкой на фиг. 2.

На фиг. 3 показана схема, иллюстрирующая фактор-граф кода LDPC (8, 2, 4) по фиг. 2. Как показано на фиг. 3, фактор-граф кода LDPC (8, 2, 4) состоит из 8 переменных узлов x₁ 300, x₂ 302, x₃ 304, x₄ 306, x₅ 308, x₆ 310, x₇ 312 и x₈ 314 и 4 узлов 316, 318, 320 и 322 проверки. Когда элемент, имеющий значение 1, то есть имеющий значение, не равное нулю, существует в точке, в которой i-ая строка и j-ый столбец матрицы проверки на четность кода LDPC (8, 2, 4) пересекаются друг с другом, между переменным узлом x_i и j-ым узлом проверки, формируется ответвление.

Поскольку матрица проверки на четность кода LDPC имеет очень небольшой вес, как описано выше, становится возможным выполнить декодирование, используя итеративное декодирование даже в блочном коде, имеющем относительно большую длину, который проявляет рабочую характеристику, приближающуюся к предельному значению пропускной способности канала для теоремы Шеннона кодирования канала, таком как турбокод, при постоянном увеличении длины блока блочного кода. Авторы MacKay и Neal доказали, что процесс итеративного декодирования кода LDPC с использованием схемы передачи потока приближается по своим рабочим характеристикам к процессу итеративного декодирования турбокода.

Для генерирования кода LDPC с высокими рабочими характеристиками следует удовлетворить следующие условия.

(1) Следует учитывать циклы фактор-графа кода LDPC.

Термин "цикл" относится к петле, формируемой ребрами, соединяющими переменные узлы с узлами проверки в фактор-графе кода LDPC, и длина цикла определена количеством ребер, составляющих петлю. Длинный цикл означает, что количество ребер, соединяющих переменные узлы с узлами проверки, составляющими петлю в фактор-графе кода LDPC, велико. В отличие от этого, короткий цикл означает, что количество ребер, соединяющих переменные узлы с узлами проверки, составляющими петлю в фактор-графе кода LDPC, невелико.

По мере того, как циклы в фактор-графе кода LDPC становятся более длинными, эффективность рабочих характеристик кода LDPC повышается по следующим причинам. Когда длинные циклы генерируют в фактор-графе кода LDPC, становится возможным предотвратить снижение такой характеристики, как минимальный уровень ошибок, возникающий, когда в фактор-графе кода LDPC существуют слишком много циклов с короткой длиной.

(2) Следует учитывать эффективное кодирование кода LDPC.

Для кода LDPC трудно выполнить кодирование в режиме реального времени по сравнению со сверточным кодом или турбокодом из-за высокой сложности кодирования. Для снижения сложности кодирования кода LDPC был предложен код повторного накопления (RA, ПН). Однако код RA также имеет ограничения в отношении снижения сложности кода LDPC. Поэтому следует учитывать эффективное кодирование кода LDPC.

(3) Следует учитывать степень распределения фактор-графа кода LDPC.

Обычно нерегулярный код LDPC обладает лучшими характеристиками по сравнению с регулярным кодом LDPC, поскольку фактор-граф нерегулярного кода LDPC имеет различные степени. Термин "степень" относится к количеству ребер, соединенных с переменными узлами, и узлами проверки в фактор-графе кода LDPC. Кроме того, фраза "распределение степени" фактор-графа кода LDPC относится к отношению количества узлов, имеющих определенную степень, к общему количеству узлов. Автор Richardson доказал, что код LDPC, имеющий определенную степень распределения, обладает лучшими характеристиками.

Далее, со ссылкой на фиг. 4, будет приведено описание матрицы проверки на четность блочного кода LDPC.

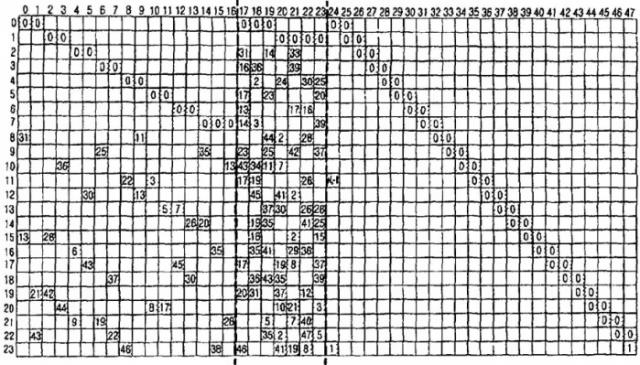
На фиг. 4 показана схема, иллюстрирующая матрицу проверки на четность общего блочного кода LDPC. Перед описанием фиг. 4, следует отметить, что блочный код LDPC представляет собой новый код LDPC, для которого не учитывается не только эффективное кодирование, но также и эффективное хранение и улучшение рабочих характеристик матрицы проверки на четность, и блочный код LDPC представляет собой код LDPC, продолженный путем обобщения структуры регулярного кода LDPC. Как показано на фиг. 4, матрица проверки на четность блочного кода LDPC разделена на множество частичных блоков, и матрицу перестановок отображают на каждом из частичных блоков. На фиг. 4 "P" представляет собой матрицу перестановок, имеющую размер N_s×N_s, и верхний индекс (или экспоненту) a_pq матрицы перестановок P равен либо 0 < a_pq < N_s-1 или a_pq = ∞.

Кроме того, "p" обозначает, что соответствующая матрица перестановок расположена в p-ой строке частичных блоков матрицы проверки на четность, и "q" обозначает, что соответствующая матрица перестановок расположена в q-ом столбце частичных блоков матрицы проверки на четность. Таким образом, представляет матрицу перестановок, расположенную в частичном блоке, где р-ая строка и q-ый столбец матрицы проверки на четность, состоящей из множества частичных блоков, пересекаются друг с другом. Таким образом, "p" и "q" представляют количество строк и количество столбцов частичных блоков, соответствующих информационной части матрицы проверки на четность соответственно.

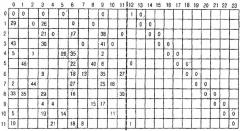
Матрица перестановок будет описана ниже со ссылкой на фиг. 5.

На Фиг. 5 показана схема, иллюстрирующая матрицу P перестановок по фиг. 4. Как показано на фиг. 5, матрица P перестановок представляет собой квадратную матрицу, имеющую размер N_s×N_s, и каждый из N_s столбцов, составляющих матрицу P перестановок, имеет вес 1, и каждая из N_s строк, составляющих матрицу P перестановок, также имеет вес 1. Здесь, хотя размер матрицы P перестановок выражен, как N_s×N_s, он также может быть выражен как N_s, поскольку матрица P перестановок представляет собой квадратную матрицу.

На фиг. 4 матрица P перестановок с верхним индексом a_pq=0, то есть матрица P° перестановок представляет собой единичную , и матрица P перестановок с верхним индексом a_pq=∞, то есть матрица P∞ перестановок представляет собой нулевую матрицу. Здесь представляет собой единичную матрицу с размером N_s×N_s.

Во всей матрице проверки на четность блочного кода LDPC, представленного на фиг. 4, поскольку общее количество строк равно N_s×p и общее количество столбцов равно N_s×q (для p ≤ q), когда вся матрица проверки на четность кода LDPC имеет полный ранг, скорость кодирования может быть выражена как уравнение (1) независимо от размера частичных блоков.

(1)

Если a_pq≠∞ для всех p и q, матрицы перестановок, соответствующие частичным блокам, представляют собой не нулевые матрицы, и частичные блоки составляют регулярный код LDPC, в котором весовое значение каждого столбца и весовое значение каждой строки в каждой из матриц перестановок, соответствующих частичным блокам, равны p и q соответственно. Здесь каждая из матриц перестановок, соответствующая частичным блокам, будет называться "частичной матрицей".

Поскольку (p-1) зависимых строк существуют во всей матрице проверки на четность, получают более высокую скорость кодирования, чем скорость кодирования, рассчитанная по уравнению (1). В случае блочного кода LDPC, если будет определено положение веса первой строки каждой из частичных матриц, составляющих всю матрицу проверки на четность, также можно будет определить положение весов для остальных строк (N_s- 1). Поэтому требуемый размер памяти уменьшается до 1/N_s по сравнению со случаем, когда веса выбирают нерегулярно для сохранения информации по всей матрице проверки на четность.

Как описано выше, термин "цикл" относится к петле, формируемой ребрами, соединяющими различные узлы с узлами проверки в фактор-графе кода LDPC, и длина цикла определяется как количество ребер, составляющих петлю. Длинный цикл означает, что количество ребер, соединяющих переменные узлы с узлами проверки, составляющими петлю в фактор-графе кода LDPC, велико. По мере того, как циклы в фактор-графе кода LDPC становятся более длинными, эффективность рабочих характеристик кода LDPC повышается.

В отличие от этого, по мере того, как циклы в фактор-графе кода LDPC становятся более короткими, возможности коррекции ошибки кода LDPC снижаются из-за деградации рабочих характеристик в результате возникновения минимального уровня ошибок. То есть в случае, когда в фактор-графе кода LDPC существует множество циклов с короткой длиной, информация о конкретном узле, принадлежащем циклу с более короткой длиной, начинающемуся от него, возвращается после небольшого количества итераций. По мере увеличения количества итераций информация возвращается к соответствующему узлу более часто, в результате чего информация не может быть правильно обновлена, что приводит к ухудшению способности коррекции ошибок кода LDPC.

Ниже, со ссылкой на фиг. 6, приведено описание структуры цикла блочного кода LDPC.

На фиг. 6 показана схема, иллюстрирующая структуру цикла блочного кода LDPC, в котором матрица проверки на четность состоит из 4 частичных матриц. Перед описанием фиг. 6, следует отметить, что блочный код LDPC представляет собой новый код LDPC, для которого учитывается не только эффективное кодирование, но также и эффективное сохранение, и улучшение рабочих характеристик матрицы проверки на четность. Блочный код LDPC также представляет собой код LDPC, расширенный путем обобщения структуры регулярного кода LDPC. Матрица проверки на четность блочного кода LDPC, представленного на фиг. 6, состоит из 4 частичных блоков, диагональная линия представляет положение, где расположены элементы, имеющие значение 1, и другие части, кроме участков, расположенных на диагональной линии, представляют собой положения, где расположены элементы, имеющие значение, равное 0. Кроме того, "P" представляет ту же матрицу перестановок, что и матрица перестановок, описанная со ссылкой на фиг. 5.

Для анализа структуры цикла блочного кода LDPC, представленного на фиг. 6, элемент, имеющий значение 1, расположенный в i-ой строке частичной матрицы P^a, определен как эталонный элемент, и элемент, имеющий значение 1, расположенный в i-ой строке, будет называться " точкой 0 ". Здесь "частичная матрица" относится к матрице, соответствующей частичному блоку. Точка 0 расположена в (i+a)-ом столбце частичной матрицы P^a.

Элемент, имеющий значение 1 в частичной матрице P^b, расположенный в той же строке, что и точка 0, называется "точкой 1". По той же причине, что и точка 0, точка 1 расположена в (i+b)-ом столбце частичной матрицы P^b.

Далее элемент, имеющий значение 1 в частичной матрице P^c, расположенный в том же столбце, что и точка 1, будет называться "точкой 2". Поскольку частичная матрица P^c представляет собой матрицу, полученную путем сдвига соответствующих столбцов единичной матрицы I вправо относительно модуля N_s на c, точка 2 расположена в (i+b-c)-ой строке частичной матрицы P^c.

Кроме того, элемент, имеющий значение 1 в частичной матрице P^d, расположенный в той же строке, что и точка 2, будет называться "точкой 3". Точка 3 расположена в (i+b-c+d)-ом столбце частичной матрицы P^d.

Наконец, элемент, имеющий значение 1, в частичной матрицу P^a, расположенный в том же столбце, что и точка 3, будет называться "точкой 4". Точка 4 расположена в (i+b-c+d-a)-ой строке частичной матрицы P^a.

В структуре цикла кода LDPC, представленного на фиг. 6, если существует цикл с длиной 4, точка 0 и точка 4 расположены в одном и том же положении. То есть взаимосвязь между точкой 0 и точкой 4 определена уравнением (2)

i i + b-c + d-a (modNs)
или	(2)
i + а i + b-c + d (modNs)

Уравнение (2) может быть переписано как уравнение (3)

a+c b + d (modNs)

(3)

В результате, когда удовлетворяется взаимозависимость по уравнению (3), генерируется цикл с длиной 4. Обычно, когда точка 0 и точка 4p представляют собой первые идентичные друг другу точки, задается соотношение i i + p(b - c + d - e)

(modN_s), и удовлетворяется следующее соотношение, показанное в уравнении (4)

p (a - b + c - d ) 0 (modNs)

(4)

Другими словами, если положительное целое число, имеющее минимальное значение среди положительных целых чисел, удовлетворяющих уравнение (4) для заданных a, b, c и d определено как "p", цикл с длиной 4p становится циклом, имеющим минимальную длину в структуре цикла блочного кода LDPC, представленного на фиг. 6.

В заключение, как описано выше, для (a-b+c-d) ≠ 0, если удовлетворяется условие gcd (N_s, a-b+c-d) = 1, тогда p = N_s. Здесь, gcd (N_s, a-b+c-d) представляет собой функцию для расчета "наибольшего общего делителя" для целых чисел N_s и a-b+c-d. Поэтому цикл с длиной 4N_S становится циклом с минимальной длиной.

Методика Richardson-Urbanke будет использоваться как методика кодирования для кода блока LDPC. Поскольку методика Richardson-Urbanke используется как методика кодирования, степень кодирования можно минимизировать, по мере того, как форма матрицы проверки на четность становится аналогичной форме полной нижней треугольной матрицы.

Ниже, со ссылкой на фиг. 7, приведено описание матрицы проверки на четность, имеющей форму, аналогичную форме полной нижней треугольной матрицы.

На фиг. 7 показана схема, иллюстрирующая матрицу проверки на четность, имеющую форму, аналогичную форме полной нижней треугольной матрицы. Матрица проверки на четность, представленная на фиг. 7, отличается от матрицы проверки на четность, имеющей форму полной нижней треугольной матрицы, формой части проверки на четность. На фиг. 7 верхний индекс (или экспонента) a_pq матрицы P перестановок информационной части составляет либо 0 ≤ a_pq ≤ N_s - 1 или a_pq = ∞, как описано выше. Матрица P перестановок с верхним индексом a_pq=0, то есть матрица P⁰ перестановок в информационной части представляет собой единичную матрицу N_s×N_s, и матрица P перестановок с верхним индексом a_pq = ∞, то есть, матрица P^∞ перестановок представляет собой нулевую матрицу. На фиг. 7 "p" представляет собой количество строк частичных блоков, отображенных на информационную часть, и "q" представляет собой количество столбцов частичных блоков, отображенных на часть проверки на четность. Кроме того, верхние индексы a_p, x и y матриц P перестановок, отображенных на часть проверки на четность, представляют собой экспоненты матрицы P перестановок. Однако, для удобства пояснения, различные верхние индексы a_p, x и y используются для различения части проверки на четность от информационной части. То есть на фиг. 7, и также представляют собой матрицы перестановок, а верхние индексы ai - a_p последовательно индексированы для частичных матриц, расположенных в диагональной части, для части проверки на четность. Кроме того, P^x и P^y также представляют собой матрицы перестановок, и для удобства пояснения они индексированы по-другому для различения части проверки на четность от информационной части. Если длина блочного кода LDPC, имеющего матрицу проверки на четность, представленную на фиг. 7, как предполагается, равна N, степень кодирования блочного кода LDPC линейно увеличивается относительно длины N (0(N)) блока.

Самая большая проблема кода LDPC, имеющего матрицу проверки на четность по фиг. 7, состоит в том, что, если длина частичного блока будет определена как N_s, будет сгенерировано N_s узлов проверки, степени которых всегда равны 1 в фактор-графе блочного кода LDPC. Узлы проверки со степенью 1 не могут повлиять на улучшение рабочих характеристик на основе итеративного декодировании. Поэтому стандартный нерегулярный код LDPC, основанный на методике авторов Richardson-Urbanke, не включает в себя узел проверки со степенью 1. Поэтому предполагается, что матрица проверки на четность по фиг. 7 представляет собой основную матрицу проверки на четность для разработки матрицы проверки на четность так, что она обеспечивает возможность эффективного кодирования, когда она не включает в себя узел проверки со степенью 1. Если матрица проверки на четность по фиг. 7 содержит частичные матрицы, выбор частичной матрицы является очень важным фактором для улучшения рабочих характеристик блочного кода LDPC, так что поиск соответствующего критерия выбора для частичной матрицы также становится очень важным фактором.

Далее будет приведено описание способа разработки матрицы проверки на четность блочного кода LDPC, на основе приведенного выше блочного кода LDPC.

Для упрощения способа разработки матрицы проверки на четность блочного кода LDPC и способа кодирования блочного кода LDPC, предполагается, что матрица проверки на четность, показанная на фиг. 7, будет сформирована с 6 частичными матрицами, как показано на фиг. 8.

На фиг. 8 показана схема, иллюстрирующая матрицу проверки на четность по фиг. 7, которая разделена на 6 частичных блоков. Как показано на фиг. 8, матрица проверки на четность блочного кода LDPC, представленная на фиг. 7, разделена на информационную часть "s", первую часть p₁ проверки на четность и вторую часть p₂ проверки на четность. Информационная часть "s" представляет собой часть матрицы проверки на четность, отображенную на действительное информационное слово в процессе кодирования блочного кода LDPC, так же, как информационная часть, описанная со ссылкой на фиг. 7, но для удобства пояснения информационная часть "s" представлена другими буквами, обозначающими ссылочные позиции. Первая часть p₁ проверки на четность и вторая часть p₂ проверки на четность представляют собой часть матрицы проверки на четность, отображаемую на действительную четность во время процесса кодирования блочного кода LDPC, так же, как и часть проверки на четность, описанная со ссылкой на фиг. 7, и часть проверки на четность разделена на две части.

Частичные матрицы A и C соответствуют частичным блокам А (802) и C (804) информационной части "s", частичные матрицы B и D соответствуют частичным блокам B (806) и D (808) первой части p₁ проверки на четность, и частичные матрицы T и E соответствуют частичным блокам T (810) и E (812) второй части p₂ проверки на четность. Хотя матрица проверки на четность на фиг. 8 разделена на 7 частичных блоков, следует отметить, что "0" не является отдельным частичным блоком, и, поскольку частичная матрица T, соответствующая частичному блоку T (810), имеет полную нижнюю треугольную форму, область, где нулевые матрицы расположены в основании диагонали, представлена "0". Процесс упрощения способа кодирования с использованием частичных матриц информационной части "s" первой части p₁ проверки на четность и второй части p₂ проверки на четность будет описан ниже со ссылкой на фиг. 10.

Частичные матрицы по фиг. 8 будут описаны ниже со ссылкой на фиг. 9.

На фиг. 9 показана схема, иллюстрирующая транспонированную матрицу частичной матрицы B, показанной на фиг. 8, частичной матрицы E, частичной матрицы T и обратной матрицы частичной матрицы T, в матрице проверки на четность по фиг. 7.

Как показано на фиг. 9, частичная матрица B^T представляет собой транспонированную матрицу частичной матрицы B, и частичная матрица T^-1 представляет собой обратную матрицу частичной матрицы T. представляет . Матрицы перестановок, представленные на фиг. 9, например , могут представлять собой единичную матрицу. Как описано выше, если верхний индекс матрицы перестановок, то есть a₁ равен 0, будет представлять собой единичную матрицу. Кроме того, если верхний индекс матрицы перестановок, то есть a₁ увеличивается на заданное значение, для матрицы перестановок будет выполнен циклический сдвиг на заданное значение, в результате чего матрица перестановок станет единичной матрицей.

Ниже, со ссылкой на фиг. 10, приведено описание процесса разработки матрицы проверки на четность блочного кода LDPC.

На фиг. 10 показана блок-схема последовательности выполнения, иллюстрирующая процедуру генерирования матрицы проверки на четность общего блочного кода LDPC. Перед описанием фиг. 10 следует отметить, что для генерирования блочного кода LDPC необходимо определить размер ключевого слова и значения скорости кодирования блочного кода LDPC, который должен быть сгенерирован, а также размер матрицы проверки на четность должен быть определен в соответствии с определенным размером ключевого слова и значением скорости кодирования. Если размер ключевого слова блочного кода LDPC представлен как N и скорость кодирования представлена как R, размер матрицы проверки на четность становится равным N(1-R)×N. В действительности, процедура для генерирования матрицы проверки на четность блочного кода LDPC, представленная на фиг. 10, выполняется только один раз, поскольку матрица проверки на четность генерируется первоначально так, чтобы она соответствовала ситуации в системе передачи данных, и после этого используют сгенерированную матрицу проверки на четность.

На фиг. 10, на этапе 1011, контроллер разделяет матрицу проверки на четность с размером N(1-R) x N в общей сложности на pxq блоков, включающих p блоков по горизонтальной оси и q блоков по вертикальной оси, и затем переходит на этап 1013. Поскольку каждый из блоков имеет размер N_s×N_s, матрица проверки на четность состоит из N_s×p столбцов и N_s×q строк. На этапе 1013 контроллер классифицирует p×q блоков, выделенных из матрицы проверки на четность, на информационную часть "s", первую часть p₁ проверки на четность и вторую часть p₂ проверки на четность, и затем переходит на этапы 1015 и 1021.

На этапе 1015 контроллер разделяет информационную часть "s" на ненулевые блоки, или ненулевые матрицы, и нулевые блоки, или нулевые матрицы в соответствии со степенью распределения, с тем, чтобы гарантировать хорошие рабочие характеристики блочного кода LDPC, и затем переходит на этап 1017. Поскольку степень распределения для гарантированно хороших рабочих характеристик блочного кода LDPC была описана выше, подробное ее описание здесь не приведено. На этапе 1017 контроллер определяет матрицы перестановок так, чтобы минимальная длина цикла для цикла блока была максимальной, как описано выше на участках ненулевых матриц в блоках, имеющих низкую степень, среди блоков, определенных в соответствии со степенью распределения, для гарантирования хороших рабочих характеристик блочного кода LDPC, и затем переходит на этап 1019. Матрицы перестановок должны быть определены с учетом циклов блоков не только по информационной части "s", но также и по первой части p₁ проверки на четность и второй части p₂ проверки на четность.

На этапе 1019 контроллер случайным образом определяет матрицы перестановок на участках ненулевой матрицы в блоках, имеющих высокую степень по сравнению с другими блоками, определенную в соответствии с распределением степени для гарантирования хороших рабочих характеристик блочного кода LDPC, и затем заканчивает процедуру. Даже когда определены матрицы Pa^pq перестановок, которые должны быть применены к участкам ненулевой матрицы в блоках, имеющих высокую степень, матрицы перестановок должны быть определены таким образом, чтобы минимальная длина цикла для цикла блока была максимизирована, и матрицу определяют с учетом циклов блоков, не только информационной части "s", но также и первой части p₁ проверки на четность и второй части p₂ проверки на четность. Пример матриц перестановок, расположенных в информационной части "s" матрицы проверки на четность, представлен на фиг. 7.

На этапе 1021 контроллер разделяет первую часть p₁ и вторую часть p₂ проверки на четность на 4 частичных матрицы B, T, D и E и затем переходит на этап 1023. На этапе 1023 контроллер вводит ненулевые матрицы и перестановок в 2 частичных блоках среди частичных блоков, составляющих частичную матрицу B, и затем переходит на этап 1025. Структура для ввода ненулевых матриц и перестановок в 2 частичных блоках среди частичных блоков, составляющих частичную матрицу B, была описана со ссылкой на фиг. 9.

На этапе 1025 контроллер вводит единичные матрицы I в диагональные частичные блоки частичной матрицы T, вводит конкретные матрицы перестановок , , …, в (i, i+1)-ые частичные блоки под диагональными компонентами частичной матрицы T, и затем переходит на этап 1027. Структура для ввода единичных матриц I в диагональные частичные блоки частичной матрицы T и ввода частичных матриц перестановок , , …, в (i, i+1)-ые частичные блоки под диагональными компонентами частичной матрицы T была описана со ссылкой на фиг. 9.

На этапе 1027 контроллер вводит частичную матрицу P^x в частичную матрицу D и затем переходит на этап 1029. На этапе 1029 контроллер вводит матрицы перестановок только в последний частичный блок в частичной матрице E и затем заканчивает процедуру. Структура для ввода 2 матриц перестановок только в последний частичный