Способ получения двумерного радиолокационного изображения объекта в большом диапазоне изменения величин эффективных площадей рассеивания локальных центров при многочастотном импульсном зондировании

Способ получения двумерного радиолокационного изображения объекта в большом диапазоне изменения величин эффективных площадей рассеивания локальных центров при многочастотном импульсном зондировании

Иллюстрации

Показать все

Реферат

Изобретение относится к области исследования радиолокационных характеристик объекта при использовании многочастотного импульсного зондирования и метода инверсного синтезирования апертуры антенны.

Методы получения радиолокационного изображения (РЛИ) основаны на цифровой обработке комплексных огибающих отраженных сигналов, измеренных в широкой полосе частот зондирующих импульсов РЛС при различных ракурсах визирования объекта.

Комплексная огибающая отраженного от объекта сигнала есть

где а - амплитуда отраженного сигнала,

R - расстояние от РЛС до объекта,

λ - длина волны зондирующего сигнала,

φ_отр - скачок фазы, возникающий при отражении от объекта.

Модель исследуемого объекта - совокупность локальных рассеивающих центров (РЦ), у которых эффективная площадь рассеивания (ЭПР) при величине λ, изменяющейся в относительно небольшой полосе |Δλ|≤0,15 λ_ср, где λ_ср - средняя в полосе перестройки длина волны, а также координаты в связанной с объектом системе отсчета являются постоянными.

Известен триангуляционный способ построения двумерного РЛИ цели в РЛС сопровождения с инверсным импульсным синтезированием апертуры [1], в котором при узкополосном импульсном зондировании цели измеряют и запоминают комплексные огибающие отраженных сигналов, их подвергают одномерному преобразованию Фурье и формируют одномерный доплеровский портрет цели путем измерения доплеровской частоты i-го РЦ и пересчета ее в линейное удаление РЦ от линии визирования цели r_ψ в направлении перпендикуляра к плоскости, проходящей через линию визирования и ось относительного вращения цели при ее сопровождении, величины r_ψ определяют для двух ракурсов сопровождения цели, разнесенных по углу визирования на интервал Δ_ψ=0,5°, по данным r_ψ1, r_ψ2, зафиксированным при углах ψ₁, ψ₂, определяют координату r_d в направлении линии визирования и по координатам

r_ψ, r_d, полученным для каждого i-го РЦ, строят РЛИ цели.

Указанному способу присущи существенные недостатки:

координата r_d при малых секторах (ψ₂-ψ₁) может быть определена только с большой погрешностью; при узкополосном зондировании разрешение РЦ является плохим; имеют место значительные трудности при идентификации образов РЦ, полученных в портретах при различных углах визирования цели. Что же касается важного для практики параметра - величины ЭПР отдельных РЦ, то в рассмотренном способе оценка его при малых секторах углов (ψ₂-ψ₁) является грубой.

Известен [2] способ построения двумерного РЛИ прямолинейно летящей цели при многочастотном узкополосном зондировании, основанный на излучении импульсных сигналов, приеме отраженных сигналов и накоплении их в течение рассматриваемого интервала синтезирования T_c, отличающийся тем, что несущую частоту зондирующих импульсов изменяют от импульса к импульсу по линейному закону в диапазоне частот от f₀ до f₀+ΔF с шагом ΔF/2^N, частоту повторения импульсов Т_и выбирают такой, что величина Т_и 2^N на порядок меньше времени корреляции траекторных нестабильностей полета цели (составляющих 25-100 мс), накопление отраженных импульсов в объеме 2^N2^N производят в 2^N этапов с интервалами между этапами Т_с/2^N, составляют матрицу с 2^N строками и 2^N столбцами, элементами которой являются амплитуды и фазы отраженных сигналов, матрицу подвергают двумерному быстрому преобразованию Фурье, полученную двумерную спектральную матрицу синтезированных откликов преобразуют в графическое матричное изображение цели, для чего определяют уровень первых боковых лепестков отклика наиболее интенсивного рассеивателя цели, принимают данный уровень за пороговую величину, сравнивают с ней величины откликов спектральной матрицы и в случае превышения порога выделяют соответствующий элемент в матричном поле 2^N2^N, а совокупность всех выделенных элементов принимают за радиолокационное изображение цели.

Описанный способ взят в качестве прототипа.

Указанный способ обеспечивает получение двумерного РЛИ, характеризуемого координатами в радиальном r_d и азимутальном r_ψ направлениях. При этом координаты r_d являются результатом преобразования во временную область спектра отраженного сигнала, размещенного в столбцах матрицы.

Величина r_d по существу является проекцией на линию визирования расстояния от РЦ до центра синтезирования. Другая координата r_ψ, получающиеся в результате преобразования Фурье строк матрицы, образованной после преобразования Фурье столбцов, является расстоянием от РЦ до плоскости, проходящей через линию визирования и ось вращения цели [3].

Недостатком указанного способа является ухудшение разрешающей способности и падение точности оценки координат и ЭПР РЦ при расширении сектора синтезирования Δ_ψ (углов поворота объекта относительно линии визирования) сверх некоторой величины, ограниченной единицами угловых градусов.

Расширение этого сектора теоретически должно приводить к повышению разрешающей способности и точности оценок [4]. Однако в рассматриваемом способе этого не происходит из-за того, что координаты r_ψ, r_d изменяются при вращении объекта, а процесс синтезирования дает их усредненную оценку. Изображение РЦ расфокусируется, падает разрешающая способность - вследствие этого способ не может обеспечить высокой точности определения координат и ЭПР РЦ, особенно в большом диапазоне изменения ЭПР РЦ.

Сущность предлагаемого изобретения заключается в следующем.

Способ решает задачу получения двумерного РЛИ объекта, обеспечивающего повышение разрешающей способности и точности определения координат и ЭПР РЦ в широком диапазоне изменения их ЭПР.

Требования к диапазону разрешаемых ЭПР РЦ в настоящее время составляет 20 дБ и более.

Технический результат, состоящий в повышении разрешающей способности в широком диапазоне изменения ЭПР РЦ и повышении точности оценки координат и ЭПР РЦ, достигается благодаря измерению с повышенной точностью частоты f сигнала и угла курса ψ объекта, являющихся параметрами процесса синтезирования РЛИ, в значительной мере определяющими качество РЛИ; реализации процесса синтезирования в виде свертки функции комплексных огибающих отраженных сигналов со специальной опорной функцией для повышения фокусировки РЛИ; использовании криволинейных координат f_x, f_z для устранения нелинейного влияния угла ψ на процесс синтезирования; оценивании в процессе синтезирования координат РЦ в связной системе отсчета (где они постоянны) для повышения точности оценивания; уточнении полученных из РЛИ оценок координат РЦ за счет использования информации об энергии комплексных огибающих; использовании уточненных координат РЦ и полученных из РЛИ оценок ЭПР РЦ для коррекции матрицы комплексных огибающих с целью изъятия из нее информации о группе РЦ с большими ЭПР, что позволяет перенести диапазон разрешаемых при синтезировании РЦ в сторону РЦ с малыми ЭПР; повторной реализации процесса синтезирования со скорректированной матрицей комплексных огибающих для получения РЛИ с малыми значениями ЭПР РЦ.

Для достижения указанного технического результата в способе получения двумерного РЛИ объекта в большом диапазоне изменения величин ЭПР локальных РЦ при многочастотном импульсном зондировании, включающем излучение импульсов с изменением несущей частоты от импульса к импульсу с шагом Δf в полосе частот ΔF, прием отраженных сигналов, измерение комплексных огибающих Ф отраженных сигналов и запоминание их в течение времени синтезирования в угловом секторе Δψ, образование матрицы комплексных огибающих и преобразование ее с помощью быстрого двумерного преобразования Фурье в матрицу синтезированных откликов, определение величины порога по уровню первых боковых лепестков наиболее интенсивного отклика, сравнение величин откликов с порогом для выделения превышающих порог элементов матрицы, совокупность которых принимают за РЛИ объекта, в котором по положению выделенных откликов в матрице синтезированных откликов определяют значения координат, а по величинам квадратов модулей откликов определяют значения ЭПР рассеивающих центров,

измеряют частоту f(t_nm) зондирующих импульсов, момент времени t_nm запоминают, где n - номер шага перестройки частоты, m - номер цикла перестройки (номер повторной перестройки), измеряют в земной системе отсчета координаты фазового центра антенны РЛС x₀, у₀, z₀ и координаты x_м(t_nm), y_м(t_nm), z_м(t_nm) точки М на объекте, выбранной в качестве центра синтезирования, измеряют относительно земной системы отсчета угол курса ψ(t_nm) связанной с объектом системы отсчета с началом в точке М, вычисляют пространственные частоты

f_x(t_nm)=-2f(t_nm)/c·sin(ψ(t_nm)-ψ₀),

где с - скорость света,

ψ₀ - угол между линией, соединяющей фазовый центр антенны РЛС с центром синтезирования, и осью z земной системы отсчета,

фазы измеренных значений комплексных огибающих Ф(t_nm) отраженных сигналов корректируют на величину 4πf(t_nm)/c·R₀(t_nm),

где R₀(t_nm) - расстояние от фазового центра антенны РЛС до точки синтезирования М,

полученные после коррекции значения комплексных огибающих Ф^*(t_nm) размещают в элементы матрицы T(k,l), двумерные номера (k,l), которых определяют по формулам

где int [•] - функция определения целой части числа,

d - шаг элементов матрицы Т по координатам f_x, f_z,

матрицу T(k,l) подвергают двумерному дискретному преобразованию Фурье

и по полученной двумерной матрице синтезированных откликов g(x,z) определяют двумерное радиолокационное изображение объекта, задают величину ρ порога разрешения по величине ЭПР рассеивающих центров и для элементов матрицы g(x,z), у которых квадрат модуля |g(x,z)|² превышает порог ρ, определяют оценки координат x_i ^*, z_i ^*, и оценки ЭПР σ_i ^* выделенных РЦ, координаты x_i ^*, z_i ^* уточняют путем поиска в окрестности каждого выделенного РЦ координат x_i ^**, z_i ^**, дающих минимум по переменным х, z функции энергии

где

R(x,z) - расстояние от фазового центра антенны РЛС до точки объекта с координатами x, z из окрестности выделенного i-го РЦ,

и по полученным оценкам ЭПР σi^* и уточненным значениям координат x_i ^**, z_i ^** выделенных РЦ определяют корректирующие поправки для комплексных огибающих

скорректированную матрицу комплексных огибающих со значениями ее элементов

подвергают двумерному дискретному преобразованию Фурье

и по полученной двумерной матрице g^*(x,z) синтезированных откликов определяют двумерное радиолокационное изображение объекта для рассеивающих центров с величинами эффективных площадей рассеивания, меньшими, чем заданный порог ρ.

Из приведенной совокупности существенных признаков предлагаемого способа следует, что общим с прототипом являются признаки излучения зондирующих импульсов с изменением несущей частоты от импульса к импульсу с шагом Δf в полосе частот ΔF, приема отраженных сигналов, измерения комплексных огибающих отраженных сигналов, запоминания их в течение времени синтезирования в угловом секторе Δψ, образования матрицы комплексных огибающих и преобразования ее с помощью двумерного быстрого преобразования Фурье в матрицу синтезированного отклика, определения уровня первых боковых лепестков отклика наиболее интенсивного рассеивателя, определения пороговой величины, равной данному уровню, сравнения с ней значений элементов матрицы, выделения элементов матрицы по условию превышения порога, определения радиолокационного изображения в виде совокупности выделенных элементов матрицы, и определения для них оценок координат и ЭПР РЦ.

Признаки образования матрицы комплексных огибающих и преобразования с помощью двумерного быстрого преобразования Фурье являются общими с прототипом только формально.

По существу же в прототипе элементы матрицы комплексных огибающих размещаются в поле переменных f, ψ; причем дискрет изменения переменных должен быть постоянным (об этом в прототипе умалчивается) для того, чтобы можно было определять r_d, r_ψ с помощью двух одномерных преобразований Фурье - сначала столбцов, затем строк матрицы. И здесь автор ошибочно употребляет понятие двумерного преобразования Фурье - в двумерном преобразовании операции со строками и столбцами матрицы переставимы, в прототипе же требуется вначале преобразование столбцов, а затем строк.

В предлагаемом способе речь идет именно о двумерном преобразовании Фурье. Причем элементы Ф(t_nm) матрицы комплексных огибающих, будучи равномерно распределенными в поле переменных f, ψ, получают неравномерное распределение в поле f_x, f_z. Этот факт является важным для практики: в предлагаемом способе не требуется равномерного вращения объекта по углу ψ, а также не требуется использования постоянного шага Δf при перестройке частот зондирующих импульсов.

Остальные вышеуказанные признаки предлагаемого способа являются отличительными.

Описание предлагаемого способа заключается в следующем.

Оператор синтезирования РЛИ, являющийся инструментом оценки неизвестных параметров (координат и ЭПР РЦ), при использовании метода максимального правдоподобия должен представлять собой интеграл свертки комплексных огибающих Ф(q), зарегистрированных в координатах вектора q, изменяющегося в интервале Δq, с опорной функцией F(q, x):

где вектор x является совокупностью неизвестных координат и ЭПР РЦ.

Опорная функция в соответствии с [5] является комплексной огибающей отраженного сигнала фиктивного РЦ, координаты x, y, z которого в связной системе отсчета произвольны:

где R₀, R - расстояния от фазового центра РЛС (точка О) до центра синтезирования (точка М) и до указанного фиктивного РЦ.

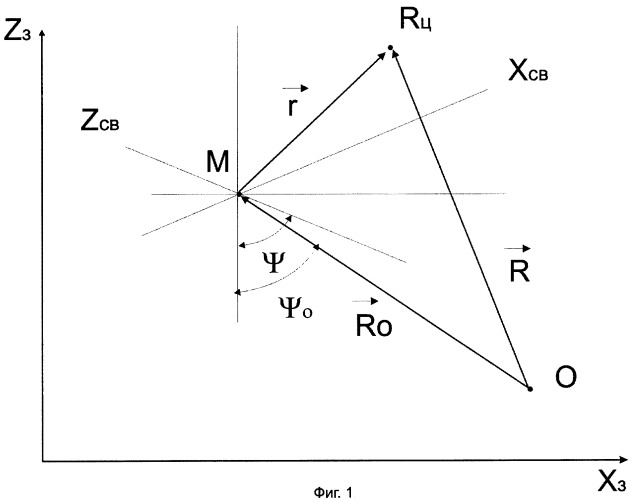
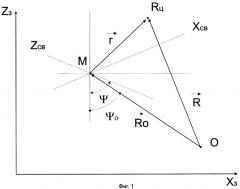
Взаимное положение точек О, М, РЦ показано на фиг.1,

где Х_з, Z_з и Х_св, Z_св - оси координат земной и связанной систем отсчета.

В связанной системе отсчета вектор есть

где

где ψ₀ - угол ориентации линии визирования (линии, соединяющей фазовый центр антенны РЛС с центром синтезирования на объекте) относительно оси z земной системы отсчета.

При R₀/R≈l соотношение (10) преобразуется к виду:

где f_x=-2/λsin(ψ-ψ₀), f_z=2/λcos(ψ-ψ₀) - пространственные частоты.

Тогда оператор синтезирования (9) для приведенных к центру синтезирования комплексных огибающих

выражается в виде:

где Ф^*(f_x, f_z) - значения Ф(t_nm), размещенные в области переменных f_x, f_z.

В выражении (16) третий сомножитель в процессе синтезирования (при изменении ψ, λ) изменяется мало.

Действительно, при R₀=900 м, λ=3 см в диапазоне изменения λ, равном ±0,15λ, для РЦ, удаленных от центра синтезирования на 1 м (т.е. при (х²+у²+z²)^0,5=1 м), величина

φ₃=4π/λ·(х²+у²+z²)/(2R₀) изменяется не более чем на ±2° от ее среднего значения (при Δλ=0).

А для РЦ с удалением от центра синтезирования на 3 м изменение φ₃ составляет ±18°.

Поскольку ошибки измерения фаз комплексных огибающих Ф^* на практике укладываются в интервале ±30°, то влиянием на процесс синтезирования третьего сомножителя в (16) можно пренебречь при указанных выше значениях дальности РЛС - объект R₀ и размера объекта (х²+у²+z²)^0,5.

И тогда оператор синтезирования РЛИ (16) становится двумерным преобразованием Фурье

Измерения Ф^* производят при дискретных значениях f, ψ, вследствие этого преобразование (17) должно быть представлено в дискретной форме. Для этого переменные интегрирования f_x, f_z заменяют номерами элементов двумерной матрицы Т

где int [•] - функция определения целой части числа,

d - шаг построения элементов матрицы.

Поскольку диапазон изменения координат f_x, f_z одинаков и равен ±2f_max/c, где f_max - максимальное значение частоты в полосе ΔF ее перестройки, то величина d может быть выбрана одинаковой для f_x и f_z.

На практике выбор величины d можно производить исходя из условия недопущения повторного размещения значений Ф^*(t_nm) в элементы матрицы Т. При этом задают размерность К матрицы Т, размещают величины Ф^*(t_nm) в элементы матрицы и фиксируют события повторного размещения. Если таковые есть, то размер матрицы увеличивают вдвое и т.д.

Опыт моделирования показывает, что размерность К матрицы Т в области переменных f_x, f_z является в 2÷4 раза большим, чем в области переменных f, ψ.

При дискретизации переменных f_x, f_z преобразование (17) в дискретной форме выражается в виде суммы

являющейся двумерным дискретным преобразованием Фурье.

Если размерность матрицы Т удовлетворяет условию К=2^P, где p - целое число, то реализация (19) выполняется с помощью быстрого двумерного дискретного преобразования Фурье.

После реализации алгоритма синтезирования (19) в полученном РЛИ выделенные по превышению порога элементы матрицы синтезированного отклика содержат информацию о координатах x, z и об ЭПР рассеивающих центров σ.

Координаты выделенных РЦ определяются по двумерному номеру отклика в матрице синтезированных откликов, а величины ЭПР РЦ - по квадрату модуля отклика, который применительно к способу-прототипу пропорционален величине σ, полосе перестройки зондирующих сигналов ΔF и интервалу времени синтезирования [6].

Моделирование показывает, что при достижимом в настоящее время уровне значений ошибок измерения амплитуды (δΔ/A≤0,5÷1 дБ) и фазы (δφ≤30°) комплексных огибающих отраженных от объекта сигналов в диапазоне перестройки частоты зондирующих импульсов от 8500 до 11500 МГц, ошибок измерения координат центра синтезирования δ_х, δ_z≤2 мм и угла курса δψ<3' синтезирование в секторе Δψ=16° обеспечивает получение оценок координат x, z и ЭПР σ РЦ с ошибками

δ_х, δ_z≤5 см, δA/А=1 дБ.

Однако это выполняется только для тех РЦ, чьи величины ЭПР находятся в диапазоне 0÷-12 дБ от уровня максимального значения ЭПР этих РЦ.

Вероятность правильного выделения (идентификации) РЦ с малыми значениями ЭПР (σ≤-12÷-20 дБ) падает от 1 при σ=-12 дБ до 0 при σ=-20 дБ.

Для расширения диапазона ЭПР правильно идентифицируемых РЦ и нахождения оценок их координат и ЭПР в предлагаемом способе информация об идентифицированных в процессе синтезирования РЦ с большими ЭПР (в диапазоне 0÷-12 дБ) изымается из исходной матрицы Т комплексных огибающих и производится повторное синтезирование с использованием скорректированной матрицы комплексных огибающих.

Однако эффективность такой коррекции существенно зависит от точности определения оценок координат РЦ.

Моделирование показывает, что используемое здесь преобразование Фурье комплексных огибающих Ф^* не реализует потенциальную точность, определяемую информацией матрицы Т. По крайней мере, точность оценок координат x, z идентифицированных (выделенных) РЦ может быть увеличена более, чем на порядок.

Достигается это применением дополнительной обработки данных, полученных в результате синтезирования РЛИ с матрицей Т. Суть ее состоит в следующем.

Задается порог ρ разрешения по ЭПР для РЦ с большими значениями ЭПР. Выделяется РЦ, чьи ЭПР превысили порог, определяются координаты выделенных РЦ x_i ^∗, z_i ^∗ и их ЭПР σ_i ^∗. Пусть количество выделенных РЦ составило I, для каждого выделенного i-го РЦ () производится уточнение координат. В окрестности точки x_i ^∗, z_i ^∗ создается область G_i(x, z) с центром в точке x_i ^∗, z_i ^∗ и радиусом δ=5÷10 см. В области G_i задается множество точек x, z с удалением друг от друга на расстоянии, меньшем δ·10^-2.

Каждая из точек x, z области G проверяется на возможность нахождения в ней выделенного РЦ.

Для этого определяются комплексные огибающие Ф_i(t_nm), создаваемые фиктивным РЦ с координатами x, z и ЭПР σ_i ^∗ для имеющегося множества измеренных значений f(t_nm), ψ(t_nm):

где R(x, z) - дальность от фазового центра антенны РЛС до точки (x, z) области G.

Комплексные огибающие отраженных сигналов от объекта, в котором удален РЦ с параметрами x, z, σ_i ^∗, находятся как

Энергия процесса, представленного всей совокупностью комплексных огибающих Ф_i ^∗(t_nm) при n= и m=, есть:

Величина Э_i(σ^∗, x, z) находится для всех точек x, z области G_i(x, z). Точка x^∗, z^∗, в которой достигается min Э_i(σ^∗, x, z) по переменным x, z, берется в качестве уточненной оценки местоположения выделенного i-го РЦ:

Реализация описанной процедуры позволяет уменьшить ошибки определения координат выделенных РЦ до 1-2 мм.

Установленные координаты i-ых выделенных РЦ xi^∗∗, z_i ^∗∗ и оценки их ЭПР σ_i ^∗ используется для удаления информации о выделенных РЦ из матрицы комплексных огибающих.

Действительно, вклад i-го РЦ с координатами x_i, z_i и ЭПР σ_i в комплексную огибающую отраженного сигнала на частоте зондирования f_n в момент времени t_nm есть:

где R(x_i, z_i) - расстояние от фазового центра антенны РЛС до точки объекта с координатами x_i, z_i в момент времени t_nm.

Это выражение в соответствии с (14) преобразуется к виду

Если известны оценки x_i ^∗∗, z_i ^∗∗, σ_i ^∗ для , то при изъятии из матрицы Т информации об i-х РЦ элементы матрицы Т корректируется на величину

Скорректированные значения комплексных огибающих есть:

Выражения (26), (27) в области переменных k, 1 запишутся как

Реализация процесса синтезирования РЛИ по данным скорректированных значений комплексных огибающих (29) производится с помощью преобразования (19).

Полученную в результате этого (повторного) преобразования матрицу синтезированных откликов преобразуют в графическое матричное изображение, в котором диапазон изменения ЭПР РЦ перенесен в область малых значений ЭПР. При этом становится возможно выделить РЦ с малыми значениями ЭПР, оценить величины координат и ЭПР этих РЦ, чего нельзя было сделать при синтезировании РЛИ по данным исходной (некорректированной) матрицы комплексных огибающих.

Построение РЛИ, основанное на использовании предлагаемого способа, проведено методом моделирования.

Задавалась модель объекта в виде совокупности неподвижных относительно связанной системы отсчета РЦ.

Зондирующие сигналы РЛС - импульсы с периодом повторения 20 мкс. Несущая частота сигнала изменялась от импульса к импульсу с шагом Δf=3000/511 МГц в полосе частот от 8500 до 11500 МГц.

Объект вращался по курсу со скоростью 12°/с.

Сектор синтезирования Δψ=16°.

РЦ в количестве 30 располагались тремя изолированными группами с удалением соседних РЦ на 40 см.

Величины σ ЭПР РЦ (или амплитуды отраженных от РЦ сигналов, равные ) задавались равными 0,1 м²; 0,01 м (-10 дБ относительно 0,1 м²) и 0,001 м ² (-20 дБ).

В каждой группе имелись РЦ с большими, средними и малыми значениями ЭПР.

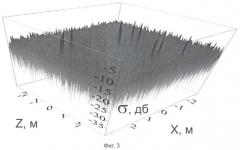
На фиг.2 приведено двумерное РЛИ, полученное при использовании исходной (некомпенсированной) матрицы комплексных огибающих отраженных сигналов, а на фиг.3 - двумерное РЛИ, полученное после компенсации информации о РЦ с ЭПР, имеющими 0 и - 10 дБ. Максимальные значения ошибок оценок координат и ЭПР компенсируемых РЦ составляли σх, σz≤2 мм, δA/А=1 дБ.

В РЛИ на фиг.2 РЦ с малыми значениями ЭПР (σ=-20 дБ) теряются на фоне изображения.

В РЛИ на фиг.3 указанные РЦ становятся доступными для идентификации.

Технический результат достигнут - устранены недостатки прототипа, а именно: повышена точность определения координат и ЭПР РЦ, а также расширен диапазон изменения ЭПР рассеивающих центров, выделяемых при получении РЛИ.

Использованные источники информации

1. Триангуляционный способ построения двумерного РЛИ цели в РЛС сопровождения с инверсным синтезированием апертуры. Патент RU 2099742 C1, кл. G01S 13/89.

2. Способ построения двумерного РЛИ прямолинейно летящей цели при многочастотном узкополосном зондировании. Патент RU 2099743 С1, кл. G01S 13/89.

3. Зиновьев Ю.С., Пасмуров А.Я. Методы обращенного синтезирования апертуры в радиолокации с помощью узкополосных сигналов. Зарубежная радиоэлектроника. №3, 1985.

4. Кондратенков Г.С., Фролов А.Ю. Радиовидение. М.: Радиотехника, 2005.

5. I. Fortuny. An Efficient 3-D Near - Field ISAR Algorithm. IEEE Transactions on Aerospace and Electronic Systems. Vol.34, №4, October 1998.

6. Митрофанов Д.Г. Формирование двумерного радиолокационного изображения цели с траекторными нестабильностями полета. Радиотехника и электроника. Том 47, №7, 2002.

Способ получения двумерного радиолокационного изображения объекта в большом диапазоне изменения величин эффективных площадей рассеивания локальных рассеивающих центров при многочастотном импульсном зондировании, включающий излучение импульсов с изменением несущей частоты от импульса к импульсу с шагом Δf полосе частот ΔF, прием отраженных сигналов, измерение комплексных огибающих Ф отраженных сигналов и запоминание их в течение времени синтезирования в угловом секторе Δψ, образование матрицы комплексных огибающих и преобразование ее с помощью быстрого двухмерного преобразования Фурье в матрицу синтезированных откликов, определение величины порога по уровню первых боковых лепестков наиболее интенсивного отклика, сравнение величин откликов с порогом для выделения превышающих порог элементов матрицы, совокупность которых принимают за радиолокационное изображение объекта, в котором по положению выделенных откликов в матрице синтезированных откликов определяют значения координат, а по величинам квадратов модулей откликов определяют значения эффективных площадей рассеивания рассеивающих центров, отличающийся тем, что измеряют частоту f(t_nm) зондирующих импульсов, момент времени измерения t_nm запоминают, где n - номер шага перестройки частоты в полосе частот ΔF, m - номер повторного цикла перестройки, измеряют в земной системе отсчета координаты фазового центра антенны радиолокационной станции (РЛС) x₀, y₀, z₀ и координаты x_м(t_nm), y_м(t_nm), z_м(t_nm) точки М на объекте, выбранной в качестве центра синтезирования, измеряют относительно земной системы отсчета угол курсаψ(t_nm) связанной с объектом системы отсчета с началом в точке М, вычисляют пространственные частотыf_x(t_nm)=-2f(t_nm)/c·sin(ψ(t_nm)-ψ₀),f_z(t_nm)=2f(t_nm)/c·cos(ψ(t_nm)-ψ₀),где с - скорость света,ψ₀ - угол между линией, соединяющей фазовый центр антенны РЛС с центром синтезирования, и осью z земной системы отсчета, фазы измеренных значений комплексных огибающих Ф(t_nm) отраженных сигналов корректируют на величину (4πf(t_nm))/c·R₀(t_nm), где R₀(t_nm) - расстояние от фазового центра антенны РЛС до точки синтезирования М, полученные после коррекции значения комплексных огибающих Ф*(t_nm) размещают в элементы матрицы T(k, l), двумерные номера которых (k, l) определяют по формуламk=int[f_x(t_nm)/d],l=int[f_z(t_nm)/d],где int [•] - функция определения целой части числа,d - шаг элементов матрицы Т по координатам f_x, f_z, матрицу T(k, l) подвергают двумерному дискретному преобразованию Фурьеg(x,z)=∑∑Ф*(k, l)exp[j2π(kx+lz)]и по полученной двумерной матрице синтезированных откликов g(x, z) определяют двумерное радиолокационное изображение объекта, задают величину ρ порога разрешения по величине эффективной площади рассеяния рассеивающих центров и для элементов матрицы g(x, z), у которых квадрат модуля |g(x,z)|² превышает порог ρ, определяют оценки координат x_i ^*, z_i ^*, и оценки эффективных площадей рассеивания σ_i* выделенных рассеивающих центров, координаты x_i*, z_i* уточняют путем поиска в окрестности каждого выделенного рассеивающего центра координат x_i**, z_i**, дающих минимум по переменным x, z функции энергии где R(x, z) - расстояние от фазового центра антенны РЛС до точки объекта с координатами x, z из окрестности выделенного i-го рассеивающего центра, и по полученным оценкам эффективных площадей рассеивания σ_i* и уточненным значениям координат х_i ^**, z_i ^** выделенных рассеивающих центров определяют корректирующие поправки для комплексных огибающих скорректированную матрицу комплексных огибающих со значениями ее элементовФ^**(k,l)=Ф^*(k,l)-Ф_кор(k,l)подвергают двумерному дискретному преобразованию Фурьеg^*(x,z)=∑∑Ф^**(k,l)ехр[j2π(kx+lz)]и по полученной двумерной матрице g^*(x,z) синтезированных откликов определяют двумерное радиолокационное изображение объекта для рассеивающих центров с величинами эффективных площадей рассеивания, меньшими, чем заданный порог ρ.