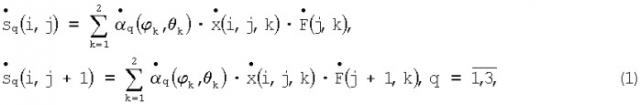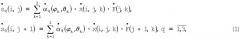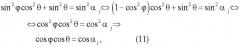Способ измерения угловых координат нескольких объектов в многоканальных доплеровских рлс

Способ измерения угловых координат нескольких объектов в многоканальных доплеровских рлс

Иллюстрации

Показать все

Реферат

Изобретение относится к радиолокации, а именно к радиолокационным системам наблюдения за объектами на базе многоканальных бортовых импульсно-доплеровских радиолокационных станций (РЛС).

Измерение угловых координат воздушных, наземных и морских объектов с помощью бортовой РЛС необходимо для посадки самолетов и вертолетов на аэродром, в интересах навигации, а также при решении разнообразных тактических задач, связанных с обнаружением объектов и обеспечением безопасности полетов.

Известен способ измерения угловых координат одиночных воздушных объектов, не разрешенных по дальности, основанный на пеленгации объектов с помощью моноимпульсной РЛС с суммарным и двумя разностными каналами, называемый моноимпульсным методом [1, с.95-105]. При этом формируется пеленгационная характеристика (пеленг), линейно зависящая от отклонения объекта по азимуту и углу места относительно равносигнального направления. Однако данный способ не работает для двух и большего числа воздушных объектов, находящихся в зоне видимости РЛС, а также не предназначен для измерения координат наземных и морских объектов. Известен способ измерения координат воздушных объектов в моноимпульсных РЛС, не разрешенных по дальности, но позволяющих разрешить их в узких диапазонах доплеровской частоты [2]. Однако этот способ не работает при неизвестном числе объектов, а также для объектов, не разрешимых по доплеровской частоте (например, неподвижных объектов). Известен также способ оценивания угловых координат известного числа N точечных источников излучения с помощью многоканальной М-элементной антенной решетки [3]. Способ основан на формировании пространственно-временной выборки отраженных сигналов, принятых в зоне видимости РЛС одновременно в М каналах, и оценивании угловых координат источников на основе критерия максимума функции правдоподобия. Однако, как и предыдущие способы, данный способ применим только для случая известного числа источников излучения (объектов), а возможная модификация способа, основанная на переборе гипотез о числе объектов, может не удовлетворять вычислительным ресурсам бортовой ЭВМ в реальном масштабе времени.

Наиболее близким по технической сущности является способ измерения угловых координат двух объектов, не разрешенных по дальности и радиальной скорости (доплеровской частоте) по данным суммарно-разностной моноимпульсной РЛС [2], который заключается в следующем.

1. При данном положении диаграммы направленности антенны (ДНА) комплексный сигнал принятый одновременно в Q измерительных каналах , , селектируется в i-x элементах разрешения по дальности: , где I - число элементов разрешения дальности.

2. В каждом i-м элементе дальности сигнал селектируется по доплеровской частоте f_j в j-x узкополосных фильтрах доплеровских частот: , где J - число таких фильтров.

3. Измеряется амплитуда U_q(i,j) сигнала , выделенного в i-м элементе дальности и j-м фильтре доплеровских частот во всех q-x каналах: q=1 - суммарный, q=2 - разностный азимутальный, q=3 - разностный угломестный канал .

4. Если в j-м фильтре доплеровских частот первого (q=1) суммарного канала (соответственно во всех Q одинаково работающих каналах) амплитуда U_q(i,j) превышает порог обнаружения (соответствуют отражению от одного или большего числа элементарных отражателей), то принимается решение о принадлежности сигналов одному или большему числу объектов, частоты отражения от которых находятся в полосе пропускания j-го фильтра доплеровских частот каждого q-го канала .

5. В суммарном канале (q=1) любым известным способом по спектральной характеристике сигнала , принятого в j-й полосе частот, находятся частоты

f_k, , k-x источников сигнала и запоминаются значения частотных характеристик для каждого k-го источника . При этом предполагается, что k-e источники (объекты) разрешены по частоте в полосе частот j-го фильтра и имеют одинаковые характеристики во всех Q=3 каналах. Также предполагается, что в силу флуктуации отраженного сигнала по частоте подобные операции можно осуществить в соседней (j+i)-й полосе частот и определить частотные характеристики этих же самых k-x источников .

6. Если число источников два (K_j=2), то измеряются значения сигналов , в j-м и (j+1)-м фильтрах q-x каналов . Эти значения связаны с комплексными амплитудами сигналов отражения от k-х объектов (k=1, 2) следующими зависимостями:

где - комплексная характеристика ДНА q-го канала в координатах азимута φ_k и угла места θ_k k-го объекта; - известное значение частотной характеристики j-го фильтра для k-го объекта (одинаковое для всех q-х каналов).

7. Из решения шести уравнений (1) находятся шесть неизвестных

и из отношения полученных величин (2) определяются пеленги:

пропорциональные отклонению k-x объектов по азимуту φ_k и углу места θ_k относительно равносигнального направления. Из равенства (2) также могут быть найдены амплитуды сигналов от объектов в i-x элементах разрешения дальности нa j-x доплеровских частотах.

Однако такой способ обладает следующими недостатками.

1. Способ опирается на метод обнаружения k-x объектов и измерения их частот f_k, по спектральной характеристике сигнала обработанного в j-й полосе частот доплеровского фильтра. Однако разрешить объекты по частоте не всегда удается, например, при пеленгации неподвижных объектов. Кроме того, подобные операции требуют определенных вычислительных затрат, а число объектов заранее не известно.

2. Если число объектов K_j в j-й полосе частот окажется больше двух, например, K_j=3, то придется увеличить число уравнений системы (1) за счет дополнительных измерений во втором соседнем (j-1)-м фильтре доплеровских частот. Использование измерений соседних фильтров доплеровских частот основано на предположении о флуктуации сигналов по частоте. Однако флуктуации носят вероятностный характер, что не гарантирует получения стабильных измерений частотных характеристик , , в трех фильтрах для всех

K_j объектов.

3. Способ не учитывает наличия помех измерений.

Технический результат направлен на измерение угловых координат произвольного числа наземных, морских и воздушных объектов, не разрешимых по дальности и доплеровской частоте, в условиях помех измерения.

Технический результат предлагаемого технического решения достигается тем, что способ измерения угловых координат нескольких объектов в многоканальных доплеровских радиолокационных станциях (РЛС) заключается в измерении отраженного сигнала в i-x элементах разрешения дальности и j-x фильтрах доплеровских частот одновременно в Q измерительных каналах , определении тех j-x фильтров доплеровских частот, где амплитуда U_q(i, j) сигнала превышает порог обнаружения, и последующей обработке совокупности полученных измерений в j-х фильтрах, отличающийся тем, что совокупность измерений располагают в составе Q-вектора измерений , который умножают справа на K×Q-матрицу весовых коэффициентов Н, вычисляемую заранее, в результате получают K-вектор оценок элементы которого , взятые по модулю, дают распределение амплитуд поля отражения нa j-й линии, являющейся линией окружности, пространственно-протяженного доплеровского элемента разрешения (ДЭР) в k-x элементах дискретизации азимута φ с повышенным в K раз разрешением по углу (при Q>K), далее в найденной последовательности амплитуд определяют угловые координаты точек максимума φ_m, , в которых амплитуда превышает порог обнаружения, а значения угла места θ_m, , берут из уравнения линии ДЭР, представленного в виде табулированной зависимости в системе координат носителя РЛС: cosφ_m cosθ_m=cosα_j, где α_j - угол отклонения луча отраженного сигнала от вектора путевой скорости движения носителя РЛС, при этом cosα_j=λ·f_i/2ν, λ - длина волны, f_j - частота j-го фильтра доплеровских частот, ν - путевая скорость носителя, и таким образом находят искомые угловые координаты φ_m(i, j), θ_m(i, j), , объектов в i-м элементе дальности и j-м ДЭР, затем указанные операции повторяют для всех значений i, j и тем самым определяют угловые координаты всех объектов в зоне видимости РЛС.

Способ осуществляется следующим образом.

1. При данном положении ДНА комплексный сигнал , принятый одновременно в Q измерительных каналах: селектируется в i-x элементах разрешения по дальности: ,

2. В каждом i-м элементе дальности сигнал селектируется по доплеровской частоте f_j в j-x узкополосных фильтрах: , .

3. Последовательность j-x элементов разрешения по частоте ставится в соответствие последовательности j-x элементов разрешения по углу α_j и вычисляется косинус этого угла по формуле

где λ - длина волны, f_j - частота j-го фильтра, ν - путевая скорость носителя.

4. Измеряется амплитуда U_q(i, j) сигнала , выделенного в i-м элементе дальности и j-м фильтре доплеровских частот во всех q-x каналах и j-x фильтрах доплеровских частот.

5. Для тех j-x фильтров доплеровских частот и q-x каналов (число таких каналов Q₁<Q), где амплитуда U_q(i, j) превышает порог обнаружения (соответствует отражению от одного или большего числа объектов), по совокупности q-x сигналов , изложенным в п.8 способом, измеряется одна угловая координата (азимут φ или угол места θ в самолетной системе координат) каждого точечного отражателя, находящегося в i, j-м ДЭР.

6. Вторая угловая координата для известного косинуса угла α_j вычисляется на основе уравнения линии ДЭР

по формуле

причем первая формула в (5) выбирается в том случае, если взятый по модулю угловой коэффициент касательной , проведенной к линии ДЭР, меньше . Иначе выбирается вторая формула. Измерение азимута при наблюдении поверхности предпочтительней, чем измерение угла места, так как в этом случае влияние боковых лепестков ДНА слева и справа (по горизонтали) оказывается равномерным.

7. Угловой коэффициент вычисляется заранее взятием производной от θ по φ:

причем его можно рассчитать только для угловых координат α, φ центра ДНА, так как в пределах узкой ДНА (например, 1°×1,5°) линии ДЭР наклонены примерно под одним и тем же углом, и слабо зависит от α и φ.

8. Измерение первой угловой координаты в п.5 осуществляется следующим образом.

8.1. Совокупность измеренных значений , располагается в составе Q-вектора измерений , который умножается справа на K×Q-матрицу весовых коэффициентов Н, вычисляемую заранее по указанной далее методике, в результате получают K-вектор оценок

8.2. Элементы , вектора оценок взятые по модулю, дают распределение амплитуд поля отражения на j-й линии пространственно-протяженного доплеровского элемента разрешения ДЭР в k-x элементах дискретизации одной угловой координаты φ (например, азимута) с повышенным в K раз разрешением по углу (при Q>K).

8.3. В найденной последовательности амплитуд определяются угловые координаты точек максимума φ_m, (например, азимута), в которых амплитуда превышает порог обнаружения, а значения второй угловой координаты (угла места) θ_m, , как уже было указано в п.6, берутся из уравнения линии ДЭР (5), представленного для ускорения вычислений в виде табулированной зависимости.

9. Таким образом находятся искомые угловые координаты φ_m (i, j), θ_m(i, j), , объектов в i-м элементе дальности и j-м ДЭР.

10. Операции пп.1-9 повторяют для всех значений i, j и тем самым определяют угловые координаты всех объектов в зоне видимости РЛС.

Расчетная часть

1. Вывод уравнения линии ДЭР сводится к следующему. Доплеровской частоте f_j ставится в соответствие угол α_j отклонения луча отраженного сигнала от вектора путевой скорости движения носителя РЛС, причем частота f_j связана с углом α_j зависимостью (например, [4], с.273):

где ν - путевая скорость; λ - длина волны РЛС.

С учетом ускорения движения носителя зависимость (8) усложняется [4]:

где r - радиальная дальность; t - время приема отраженного сигнала.

В элементах разрешения дальности коническая поверхность постоянного угла α_j (частоты f_j), имеющая общую вершину с конической поверхностью ДНА, пересекает сферическую поверхность уровня дальности в пределах ДНА по линии окружности, какой и является линия ДЭР. Центр данной окружности лежит на оси ОХ прямого кругового конуса постоянного значения угла α_j. По этой же оси направлен вектор путевой скорости. В самолетной системе координат положительная полуось ОХ совмещается с вектором скорости . Тогда линия ДЭР (линия окружности) без искажения проецируется по плоскость YOZ. Уравнение окружности с центром в начале координат и радиусом R в плоскости YOZ:

Связь прямоугольных y, z и сферических r, φ, θ (дальность, азимут, угол места) координат произвольной точки, лежащей на окружности, устанавливается обычным образом:

После подстановки (3) в (2) получается уравнение линии ДЭР:

где θ∈[0,90°], α_j∈[0°,90°], φ∈(-90°,90°). Угол места θ при наблюдении за поверхностью отсчитывается в положительном направлении по часовой стрелке от горизонтальной плоскости XOY, азимут φ - против часовой стрелки от оси ОХ (направления движения носителя РЛС).

Уравнение (11) линии ДЭР связывает угловые координаты азимута φ и угла места θ точки в пространстве, принадлежащей линии ДЭР в пределах ДНА, с косинусом угла α_j, зависящим от доплеровской частоты f_j в соответствии с (8), в самолетной системе координат.

2. Методика измерения (оценивания) первой угловой координаты (например, азимута) сводится к следующему. Пусть в i-м элементе дальности, в j-м фильтре доплеровских частот нескольких q-x приемных каналов (общим числом Q₁≤Q) зафиксированы (измерены) значения отраженных сигналов от неизвестного числа точечных объектов, расположенных нa j-й линии ДЭР, амплитуды которых превысили порог обнаружения. Модель измерений имеет вид следующей суммарной линейной зависимости:

где суммирование ведется в области пересечения q-x ДНА по k-м элементам дискретизации азимута φ_k или угла места θ_k, связанным между собой уравнением (11) линии ДЭР в системе координат носителя РЛС:

причем с вычислительной точки зрения зависимость (13) целесообразно табулировать; - комплексная амплитуда (огибающая [5]) сигнала, отселектированного в i-м элементе дальности, j-м фильтре доплеровских частот q-го канала; - комплексные коэффициенты ДНА q-го канала, взятые в координатах φ_k, θ_k k-го элемента дискретизации относительно центра q-й ДНА в системе координат носителя; - искомые комплексные амплитуды поля отражения в k-x элементах дискретизации на линии ДЭР; - комплексная помеха типа белого шума.

Совокупность q-x измерений (12) при фиксированных i, j описывается векторно-матричной моделью [6]:

где - вектор измерений ;

A - Q₁×K-матрица коэффициентов ДНА и ленточного типа; К-вектор искомых комплексных амплитуд ; - вектор помех .

В описании (14) решается задача нахождения вектора оптимальных оценок по методу наименьших квадратов (МНК), при этом МНК-оценки имеют стандартный вид (например, [6]):

где δ - параметр регуляризации, необходимый для обращения матрицы А^*T А; *Т - символ комплексного сопряжения и транспонирования; Е - единичная матрица; Н - матрица комплексных весовых коэффициентов, вычисляемая заранее. Точность оценивания по формуле (15) при δ→0 характеризуется корреляционной матрицей ошибок оценивания . Для некоррелированных помех

p_q(i, j) с дисперсией дисперсия ошибки оценивания отдельного элемента вектора составляет , где tr - след матрицы, и уменьшается с увеличением числа каналов Q₁.

Предложенный способ позволяет измерять угловые координаты неизвестного числа точечных отражателей (объектов) в составе доплеровских элементов разрешения, что отличает его от ранее известных прототипов. Помимо измерения координат воздушных объектов, способ позволяет измерять угловые координаты наземных и надводных объектов. На основе измеренных координат всех точечных отражателей может быть построено трехмерное изображение поверхности.

Литература

1. Леонов А.И., Фомичев К.И. Моноимпульсная радиолокация. М.: Радио и связь, 1984. 312 с.

2. Жибуртович Н.Ю., Абраменков В.В., Савинов Ю.И., Климов С.А., Чижов А.А. Определение радиолокационной системой с моноимпульсным пеленгатором угловых координат отдельных целей из состава группы // Радиотехника. 2005, №6. С.38-41.

3. Сычев М.И. Оценивание угловых координат близко расположенных источников излучения по пространственно-временной выборке // Радиоэлектроника. 1991, №5. С.33-39.

4. Кондратенков Г.С., Фролов А.Ю. Радиовидение. Радиолокационные системы дистанционного зондирования Земли. Учебное пособие для вузов / Под ред. Г.С.Кондратенкова. М.: Радиотехника, 2005. 368 с.

5. Радиолокационные станции с цифровым синтезированием апертуры антенны / В.Н.Антипов, В.Т.Горяинов, А.Н.Кулин, Толстов Е.Ф. и др. Под ред. В.Т.Горяинова. М.: Радио и связь, 1988. 304 с.

6. Клочко В.К. Методы оптимального восстановления радиолокационных изображений поверхности // Автометрия. 2005. Т.41. №6. С.62-73.

Способ измерения угловых координат нескольких объектов в многоканальных доплеровских радиолокационных станциях (РЛС), заключающийся в измерении отраженного сигнала в i-x элементах разрешения дальности и j-x фильтрах доплеровских частот одновременно в Q измерительных каналах определении тех j-x фильтров доплеровских частот, где амплитуда Uq(i,j) сигнала превышает порог обнаружения, и последующей обработке совокупности полученных измерений в j-x фильтрах, отличающийся тем, что совокупность измерений располагают в составе Q-вектора измерений Y, который умножают справа на K×Q-матрицу весовых коэффициентов Н, вычисляемую заранее, в результате получают К-вектор оценок элементы которого взятые по модулю, дают распределение амплитуд поля отражения на j-й линии, являющейся линией окружности, пространственно-протяженного доплеровского элемента разрешения (ДЭР) в k-x элементах дискретизации азимута φ с повышенным в К раз разрешением по углу (при Q>K), далее в найденной последовательности амплитуд определяют угловые координаты точек максимума φ_m, в которых амплитуда превышает порог обнаружения, а значения угла места θ_m, берут из уравнения линии ДЭР, представленного в виде табулированной зависимости в системе координат носителя РЛС: cos φ_m cosθ_m=cos α_j, где α_j - угол отклонения луча отраженного сигнала от вектора путевой скорости движения носителя РЛС, при этом cos α_j=λ·f_j/2ν, λ - длина волны, f_j частота j-го фильтра доплеровских частот, ν - путевая скорость носителя, и таким образом находят искомые угловые координаты φ_m(i,j), θ_m(i,j), объектов в i-м элементе дальности и j-м ДЭР, затем указанные операции повторяют для всех значений i,j и тем самым определяют угловые координаты всех объектов в зоне видимости РЛС.