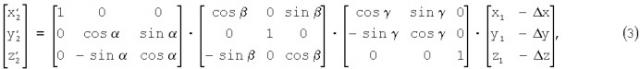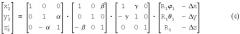Способ формирования радиолокационного изображения в бортовых системах радиовидения

Способ формирования радиолокационного изображения в бортовых системах радиовидения

Иллюстрации

Показать все

Реферат

Изобретение относится к системам активной и пассивной радиолокации наблюдения за наземной и воздушной обстановкой на базе бортовых многоканальных (с антенными решетками), а также сканирующих радиолокационных и теплолокационных станций (РЛС, РТЛС) миллиметрового диапазона и может быть отнесено также к системам оптической локации.

При наблюдении за наземной и воздушной обстановкой во времени t на базе бортовых радиолокационных и радиотеплолокационных станций (РЛС, РТЛС) миллиметрового диапазона формируется матрица амплитудного радиолокационного или радиотеплолокационного изображения (РЛИ, РТЛИ) в элементах дискретизации угловых координат (угла места и азимута) с привязкой к текущему дискретному моменту времени обзора t_µ, , например, [1]. Для трехмерных РЛИ формируется совокупность таких матриц в элементах разрешения дальности или две матрицы: матрица амплитуд и матрица третьей координаты (дальности) в элементах дискретизации угловых координат. Данные матрицы с помощью алгоритмов отображения выводятся на экран индикатора, и пилот носителя РЛС или РТЛС имеет возможность наблюдать последовательность кадров. Однако качество таких изображений снижено наличием шумовых (зернистых) пятен на изображениях из-за недостаточно высокого отношения сигнал-шум, а также смазыванием изображения из-за вибрации летательного аппарата. Возникает проблема повышения качества изображения за счет совместной обработки кадров РЛИ (РТЛИ) во времени t и устранения смазываний.

Известны способы устранения смазываний отдельных кадров изображения, основанные на методах восстановления (реконструкции) изображений (например, [2]), искаженных измерительным прибором или диаграммой направленности антенны ДНА) с известной аппаратной функцией искажения (смазывания), например, функция равномерного смазывания. Однако вибрации носителя с привязкой к одному дискретному моменту времени t_µ приводят к смазыванию изображения в случайном направлении, которое не поддается описанию. Следовательно, проблема устранения смазывания может быть решена в последовательности моментов времени t_µ одновременно с решением задачи совмещения кадров.

Наиболее близким по технической сущности является способ формирования двумерного и трехмерного РЛИ поверхности с повышенной разрешающей способностью по угловым координатам [1] с привязкой к одному моменту времени обзора, который заключается в восстановлении матрицы изображения в элементе разрешения дальности и сводится к следующим операциям.

1. В q-x приемных элементах антенной решетки РЛС или q-x каналах сканирующей по углу места (по i) и азимуту (по j) антенны РЛС с привязкой к текущему моменту времени обзора t_µ измеряются амплитуды отраженных сигналов S_q(t_µ,i,j), , , в k-x элементах дальности , где I×J - размер зоны обзора, K - число элементов разрешения дальности.

2. Эти амплитуды обрабатывают, умножая их на весовые коэффициенты, расчет которых осуществляют заранее по определенной методике.

3. В результате получают оценки , , , , представляющие восстановленное амплитудное изображение наземной или воздушной обстановки с повышенным в несколько раз разрешением по угловым координатам в момент времени t_µ.

4. Найденные оценки помещают в две матрицы: матрицу A(t_µ,i,j) амплитудного изображения зоны обзора в i,j-x элементах дискретизации угла места и азимута и матрицу дальностей R(t_µ,i,j) до i,j-го элемента наблюдаемой поверхности или объекта, которые с помощью алгоритмов отображения выводят на экран индикатора. Предусмотрен пересчет матриц в прямоугольную систему координат.

5. Способ применим также для РТЛС. Применительно к РТЛС под элементом дальности понимается диапазон дальности в зоне обзора (K=1). Поэтому РТЛИ, в отличие от РЛИ, для фиксированного положения РТЛС в пространстве получается двумерным: A(t_µ,i,j).

Однако данный способ обладает следующими недостатками.

1. Способ не предусматривает совместной (пространственно-временной) обработки кадров РЛИ (РТЛИ), полученных в разные периоды обзора в дискретные моменты времени t_µ, , повышающей отношение сигнал-шум.

2. Способ не учитывает и соответственно не устраняет смазываний изображений из-за вибрации носителя РТЛ (РТЛС).

Указанные недостатки приводят к снижению качества изображений, что выражается в появлении шумовых (зернистых) пятен на изображении из-за недостаточного отношения сигнал-шум, а также размывании контуров объектов на изображении из-за смазываний.

Технический результат направлен на устранение указанных недостатков, то есть на повышение качества изображения в РЛС и РТЛС.

Технический результат предлагаемого технического решения достигается тем, что способ формирования радиолокационного изображения в бортовых системах радиовидения заключается в формировании в каждый дискретный µ-й момент времени t_µ обзора участка поверхности или воздушного пространства матрицы амплитудного изображения зоны обзора A(t_µ,i,j) и матрицы дальностей R(t_µ,i,j) в i,j-x элементах дискретизации угла места и азимута, , I×J - размер зоны обзора, отсчитываемых в прямоугольной антенной системе координат, отличающийся тем, что операции формирования матриц A(t_µ,i,j) и R(t_µ,i,j) повторяют в каждый дискретный момент времени обзора t_µ, µ=1,2,…,L, при этом матрицы A(t_µ-1,i,j) и R(t_µ-1,i,j), полученные в предыдущий (µ-1)-й момент времени, экстраполируют на момент времени t_µ с помощью преобразования координат: поворота осей и параллельного переноса по данным навигационной системы, и экстраполированные матрицы А^Э(t_µ,i,j), R^Э(t_µ,i,j) ставят в соответствие текущим матрицам A(t_µ,i,j), R(t_µ,i,j) и затем сравнивают амплитуды и дальности элементов в центральной области изображений, между которыми установлено соответствие, затем это соответствие уточняют корреляционно-экстремальным методом совмещения кадров и тем самым уменьшают ошибки навигационных измерений, далее указанные операции повторяют в последовательности моментов времени t_µ, µ=1,2,…,L, а найденные значения A(t_µ,i,j) и R_µ(t_µ,i,j) усредняют во времени t, что компенсирует ошибки измерения и округления до элементов дискретизации, в результате к моменту t_L формируют две усредненные матрицы: и , относительно каждого i,j-го элемента которых строится плавающее окно малого размера M₁×N₁=(2m₁+1)×(2n₁+1), которое меняет свое положение, смещаясь построчно на один элемент дискретизации, и значения и элементов, взятые в этом окне, суммируют по i₁ и j₁ с весовыми коэффициентами h(i₁,j₁), расчет которых осуществляют заранее, в результате получают оценки амплитуд

и аналогично (1) получают оценки дальностей восстановленного изображения в центральном элементе окна, затем полученные по совокупности i,j-x элементов оценки , , , располагают в составе (I-2m₁)×(J-2n₁)-матриц А и R, которые представляют трехмерное изображение наземной или воздушной обстановки.

Способ осуществляется следующим образом.

1. В каждый дискретный момент времени t_µ, µ=1,2,…,L, формируются двумерные A(t_µ,i,j) или трехмерные: A(t_µ,i,j) и изображения в соответствии с известными способами восстановления изображений.

2. Координаты х₁, y₁ центра каждого i,j-го элемента матриц A(t_µ-1,i,j) и R(t_µ-1,i,j), взятые в антенной системе координат o, x, y, z, на основе навигационных данных об углах поворота осей ox, oy, oz и параллельном смещении носителя РЛС или РТЛС Δx, Δy, Δz экстраполируются на момент времени t_µ в координаты , и округляются до ближайших элементов дискретизации i', j'.

3. Если i', j' попадают в поле матриц A(t_µ,i,j), R(t_µ,i,j), то значения i,j-x элементов матриц A(t_µ-1,i,j), R(t_µ-1,i,j) переписываются в соответствующие i',j'-e элементы экстраполированных матриц A^Э(t_µ,i,j), R^Э(t_µ,i,j). Установленное соответствие между i, j и i', j' запоминается. В противном случае фиксируется непопадание i', j'.

4. Для компенсации ошибок измерения навигационной системы положение матриц A^Э(t_µ,i,j), R^Э(t_µ,i,j) относительно A(t_µ,i,j), R(t_µ,i,j) корректируется корреляционно-экстремальным методом, и устанавливается соответствие между элементами матриц. Изменения запоминаются.

5. Операции п.п.1-4 повторяются в последовательности моментов времени t_µ, а найденные значения А(t_µ,i,j) и R_µ(t_µ,i,j) усредняются во времени t. В результате к моменту t_L формируются две матрицы: и .

6. Относительно каждого i,j-го элемента матриц и строится плавающее окно размера M₁×N₁=(2m₁+1)×(2n₁+1), меньшего, чем ширина диаграммы направленности антенны (ДНА на уровне 0,5 мощности) M×N=(2m+1)×(2n+1) в числе элементов дискретизации угла места по i и азимута по j: m₁<m, n₁<n.

7. Окно меняет свое положение, смещаясь построчно на один элемент дискретизации, и значения и элементов, взятые в этом окне, суммируются по i₁ и j₁ с весовыми коэффициентами h_k(i₁,j₁), расчет которых осуществляется по методике восстановления изображений, указанной ниже, в результате получаются оценки

восстановленного изображения в центральном элементе окна.

8. Полученные по совокупности i,j-x элементов оценки , R(i,j), , располагают в составе (I-2m₁)×(J-2n₁)-матриц А и R, которые представляют улучшенное трехмерное изображение. В частном случае двумерного изображения формируется только одна матрица А.

Математические расчеты, положенные в основу способа, сводятся к следующему.

Носитель РЛС или РТЛС находится в самолетной прямоугольной системе координат, центр которой совмещен с центром носителя, ось OY совпадает с вектором скорости движения носителя, а ось ОХ расположена в плоскости правого крыла. Антенна в момент времени t_µ-1 находится в прямоугольной системе координат O₁X₁Y₁Z₁, а в момент t_µ - в системе O₂X₂Y₂Z₂, которые расположены определенным образом относительно самолетной системы. Оси O₁Z₁ и O₂Z₂ представляют линию визирования антенны. Так как между самолетной и антенной системами существует известная связь, то ограничимся рассмотрением одной антенной системы во времени t. При движении объекта носителя РТЛС на промежутке [t_µ-1, t_µ] осуществляется поворот осей О₁Х₁, O₁Y₁ и O₁Z₁ на углы α, β, γ (тангаж, крен, курс), а точка O₁ получает приращения параллельного переноса Δх, Δy, Δz.

Координаты центральной точки M(x₁,y₁,z₁), z₁=0, i,j-го элемента матрицы двумерного изображения, взятой в системе O₁X₁Y₁Z₁, пересчитываются в координаты системы O₂X₂Y₂Z₂ в соответствии с формулами поворота осей и параллельного переноса:

причем для двумерных матриц A(t_µ,i,j) и R(t_µ,i,j) не используется.

В вычислительном плане при малых углах поворота α, β, γ формула (3) упрощается:

Полученные по формулам (3) или (4) координаты , округляются до ближайшего элемента дискретизации i', j'. Для снижения влияния ошибок измерения навигационной системы и округления корректируется соответствие между элементами матриц изображения, полученных в моменты времени t_µ-1 и t_µ. Для этого используется пространственно-временная обработка на основе корреляционно-экстремального метода совмещения и осреднения кадров изображения [3], который покажем на примере одной матрицы амплитудного изображения.

1. Пусть в момент t_µ-1 получена матрица А_µ-1=(A(t_µ-1,i,j)), которая ставится в соответствие матрице A_µ=(A(t_µ,i,j)). На основе данных навигационной системы о движении объекта носителя РЛС или РТЛС (измерений углов поворота α, β, γ и смещений Δx, Δy, Δz) координаты центра х₁, y₁ каждого i,j-го элемента матрицы А_µ в соответствии с формулами (3) или (4) пересчитываются на момент t_µ, то есть находятся экстраполированные значения координат , и соответствующие им номера i', j', при этом z₁ в (3), (4) полагается равным нулю (плоское изображение), а координата не используется. Значения элементов матрицы А_µ-1=(A(t_µ-1,i,j)) переписываются в матрицу экстраполированного изображения по всем элементам i', j', координаты которых попадают в поле 2-го кадра А_µ, в противном случае для i', j' фиксируются пропуски.

2. Рассматривается центральная часть матрицы - область D, в которой пропуски заведомо отсутствуют. Даются приращения координатам i, j по всем элементам матрицы в области D на малое число элементов дискретизации Δi, Δj, а также дополнительное приращение смещению Δz в формулах (3) или (4). Оптимальные значения Δi, Δj, Δz определяются критерием близости двух изображений: и

А_µ, например:

3. На основе найденных значений Δi, Δj, Δz корректируются экстраполированные номера i', j'. Тем самым устанавливается более точное соответствие между элементами соседних матриц РЛИ (РТЛИ) в смысле принадлежности каждой пары этих элементов одному и тому же элементу поверхности или наблюдаемого наземного (воздушного) объекта и, как следствие, уменьшается влияние ошибок измерения и округления на пересчет координат, вследствие чего повышается точность формирования РЛИ (РТЛИ).

4. Амплитуды соответствующих элементов соседних кадров усредняются во времени t с помощью известных рекуррентных фильтров [3]. При усреднении сглаживаются ошибки измерения и повышается отношение сигнал-шум, что приводит к повышению разрешающей способности РТИ по угловым координатам. Одновременно сглаживаются шумовые (зернистые) пятна на изображении. Как следствие, повышается качество изображения.

5. В случае формирования трехмерного изображения выполняются аналогичные операции со второй матрицей R(t_µ,i,j), а критерий (5) принимает комплексный вид (члены суммы (5) для матриц амплитуд и дальностей берутся с весовыми коэффициентами).

Для снижения влияния вибраций на качество изображения предлагается следующее. К вибрациям можно отнести как физическое "дрожание" носителя РЛС (РТЛС), так и накапливающиеся случайные ошибки измерения и округления до элементов дискретизации. При длительном осреднении кадров указанные ошибки, а также помехи суммируются, и к моменту времени t_L получается равномерно смазанное изображение с повышенным отношением сигнал-шум. Для частичного устранения влияния вибраций рассматривается модель равномерного смазывания матриц в малой окрестности каждого i,j-го элемента, которую рассмотрим на примере амплитудного изображения:

где - амплитудное изображение, смазанное за счет вибраций; A(j,j) - искомое изображение как функция двух переменных i, j; P(i,j) - центрированные гауссовские помехи; m₁<m, n₁<n (например, m₁=n₁=1).

Модель (6) отличается от более общих моделей тем, что коэффициенты смазывания (аппаратная функция g) тождественно равны единице: g(i,j)=1,∀i,j. В модели (6) число измерений меньше числа оцениваемых параметров. Решение такой некорректной задачи заключается в нахождении псевдо-оптимальных МНК-оценок A(i,j) с введением процедур регуляризации [2]. Алгоритм восстановления сводится к следующему.

1. Относительно каждого i,j-го элемента, , , искомой матрицы изображения А строится плавающее окно ограниченного размера M₁×N₁=(2m₁+1)×(2n₁+1), которое меняет свое положение, смещаясь построчно на один элемент дискретизации.

2. Амплитуды А(i+i₁,j+j₁), взятые в этом окне, суммируются по i₁ и j₁ с весовыми коэффициентами h_k(i₁,j₁), расчет которых осуществляется заранее по методу наименьших квадратов (МНК) [2]. В результате получается оценка

восстановленного изображения в центральном элементе окна.

3. Полученные по совокупности i,j-x элементов оценки , , , располагаются в составе (I-2m₁)×(J-2n₁)-матрицы А, которая представляет улучшенное изображение.

Для расчета весовых коэффициентов в (7) модель (6) представляется в векторно-матричной форме:

где

- M₁N₁ - вектор-столбец смазанных оценок (7), взятых в окрестности i,j-го элемента; G - M₁N₁×(M₁+2m₁)(N₁+2n₁) - матрица ленточного типа с единичными элементами; - вектор-столбец искомых оценок; - вектор-столбец помех.

Оценивание вектора (8) осуществляется в соответствии со стандартной процедурой МНК (например, [2]):

где Н - матрица весовых коэффициентов; Е - единичная матрица; δ - параметр регуляризации, необходимый для обращения матрицы G^T G в тех случаях, когда число измерений меньше числа оцениваемых параметров; Е - символ транспонирования.

В качестве оценки (7) берется центральный элемент вектора (9) с наименьшей дисперсией ошибки оценивания. Весовые коэффициенты h(i,j) в (7) - это элементы центральной строки матрицы весовых коэффициентов Н, найденной в (9).

Предложенный способ позволяет повысить качество двумерных или трехмерных изображений поверхности, наземной или воздушной обстановки за счет пространственно-временной обработки последовательности кадров изображения и устранения влияния вибраций носителя РЛС или РТЛС. Способ может найти применение в бортовых системах активной и пассивной радиолокации, а также в оптических системах.

Литература

1. Патент RU 2292060 С1. Способ наблюдения за воздушными объектами и поверхностью на базе бортовой РЛС / В.К.Клочко. МПК: G01S 13/02. Приоритет 28.06.2005. Опубл.: 20.01.2007. Бюл. №2.

2. Клочко В.К. Методы оптимального восстановления радиолокационных изображений поверхности // Автометрия. 2005. Т.41. №6. С.62-73.

3. Баклицкий В.К., Юрьев А.Н. Корреляционно-экстремальные методы навигации. М.: Радио и связь, 1982, 256 с.

Способ формирования радиолокационного изображения в бортовых системах радиовидения, заключающийся в формировании в каждый дискретный µ-й момент времени t_µ обзора участка поверхности или воздушного пространства матрицы амплитудного изображения зоны обзора A(t_µ,i,j) и матрицы дальностей R(t_µ,i,j) в i, j-x элементах дискретизации угла места и азимута, I×J - размер зоны обзора, отсчитываемых в прямоугольной антенной системе координат, отличающийся тем, что операции формирования матриц A(t_µ,i,j) и R(t_µ,i,j) повторяют в каждый дискретный момент времени обзора t_µ, µ=1,2,…,L, при этом матрицы A(t_µ-1,i,j) и R(t_µ-1,i,j), полученные в предыдущий (µ-1)-й момент времени, экстраполируют на момент времени t_µ с помощью преобразования координат: поворота осей и параллельного переноса по данным навигационной системы, и экстраполированные матрицы A^Э(t_µ,i,j), R^Э(t_µ,i,j) ставят в соответствие текущим матрицам A(t_µ,i,j), R(t_µ,i,j) и затем сравнивают амплитуды и дальности элементов в центральной области изображений, между которыми установлено соответствие, затем это соответствие уточняют корреляционно-экстремальным методом совмещения кадров и тем самым уменьшают ошибки навигационных измерений, далее указанные операции повторяют в последовательности моментов времени t_µ, µ=1,2,…,L, а найденные значения A(t_µ,i,j) и R(t_µ,i,j) усредняют во времени t, что компенсирует ошибки измерения и округления до элементов дискретизации, в результате к моменту t_L формируют две усредненные матрицы: относительно каждого i,j-го элемента которых строится плавающее окно малого размера M₁×N₁=(2m₁+1)×(2n₁+1), которое меняет свое положение, смещаясь построчно на один элемент дискретизации, и значения и элементов, взятые в этом окне, суммируют по i₁ и j₁ с весовыми коэффициентами h(i₁,j₁), расчет которых осуществляют заранее, в результате получают оценки амплитуд и аналогично получают оценки дальностей восстановленного изображения в центральном элементе окна, затем полученные по совокупности i,j-x элементов оценки располагают в составе (I-2m₁)×(J-2n₁)-матриц А и R, которые представляют трехмерное изображение наземной и воздушной обстановки.