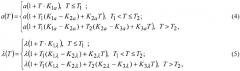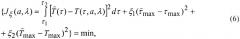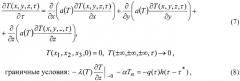Способ определения комплекса теплофизических свойств твердых материалов

Способ определения комплекса теплофизических свойств твердых материалов

Иллюстрации

Показать все

Реферат

Изобретение относится к теплофизическим измерениям. Область применения - определение теплофизических свойств (ТФС) материалов и изделий неразрушающим методом.

Известен способ идентификации комплекса теплофизических свойств твердых материалов, включающий воздействие тепловыми импульсами от линейного источника на плоскую поверхность исследуемого и эталонного образцов, измерение избыточных температур в момент подачи тепловых импульсов в точках, расположенных на фиксированных расстояниях от линии нагрева на поверхности образцов, по идентифицированным параметрам теплофизических свойств образцов и действительным значениям теплофизических свойств эталона находят искомый комплекс теплофизических свойств (патент РФ №2125258, 1999 г., МПК: G01N 25/18 (2006.01)). Под избыточной температурой понимается температура, отсчитываемая от начальной температуры, при которой находился образец в момент подачи первого теплового импульса. Под эталонным образцом понимается образец материала с известными теплофизическими свойствами.

Известен также способ идентификации комплекса теплофизических свойств твердых материалов, включающий тепловое импульсное воздействие от линейного источника нагрева на плоскую поверхность исследуемого и эталонного образцов, измерение избыточной температуры на плоской поверхности образцов на фиксированном расстоянии от линии нагрева с момента подачи теплового импульса, причем тепловое импульсное воздействие и измерение избыточной температуры осуществляют в плоскости контакта исследуемого и эталонного образцов, а измерение избыточной температуры производят в одной точке в заданном интервале времени, используя математическую модель прямой задачи теплопроводности на основе метода конечных разностей (решение о выдаче патента на изобретение по заявке 2005117325/28 от 06.06.2005, МПК: G01N 25/00 (2006.01)). Этот способ принят за ближайший аналог.

Недостатками способов являются низкая точность измерений и длительное время проведения измерений.

Техническим результатом изобретения является повышение точности определения комплекса теплофизических свойств твердых материалов и упрощение теплофизических измерений.

Технический результат достигается тем, что в способе определения комплекса теплофизических свойств твердых материалов, заключающемся в тепловом импульсном воздействии на плоскую поверхность исследуемого образца, измерении избыточной температуры на плоской поверхности образца с момента подачи теплового импульса в одной точке в заданном интервале времени, причем тепловое импульсное воздействие на плоскую поверхность образца осуществляют лучистым тепловым потоком известной плотности и длительности, а измерение избыточной температуры с момента подачи теплового импульса проводят в центральной части нагреваемой поверхности образца, при этом регистрируют значение максимальной избыточной температуры и время ее достижения, используя математическую модель прямой задачи теплопроводности на основе метода конечных разностей, применяют промежуточную сеточную функцию источника нагрева излучением и конвективного теплообмена:

для учета нелинейной зависимости теплофизических свойств материала от температуры используются кусочно-линейные функции (принято условное разбиение шкалы избыточной температуры на три участка [0;Т₁],(Т₁;Т₂],(Т₂,∞)):

решают обратную коэффициентную задачу теплопроводности вариационным методом на интервале наблюдения избыточной температуры [τ₁,τ₂], при выборе параметра регуляризации по невязке:

искомые теплофизические свойства а, λ находят из минимума функции J_ξ(а,λ),

где Т^k _m,n,p - сеточная функция;

Т - избыточная температура, регистрируемая в эксперименте;

- избыточная температура, рассчитанная математической моделью;

T_max - максимальное значение избыточной температуры, регистрируемое в эксперименте;

- максимальное значение избыточной температуры, рассчитанное математической моделью;

Т₁ - избыточная температура, регистрируемая в момент времени τ₁,

Т₂ - избыточная температура, регистрируемая в момент времени τ₂;

τ_max - момент времени регистрации избыточной температуры Т_max;

- момент времени, рассчитанный математической моделью и соответствующий температуре ;

а - температуропроводность;

λ - теплопроводность;

m - номер отсчета по координате х,

n - номер отсчета по координате у,

р - номер отсчета по координате z,

x, y, z - оси правой декартовой прямоугольной системы координат;

k - номер отсчета по времени;

h - шаг сетки по расстоянию;

Δτ - шаг сетки по времени;

q - плотность теплового потока;

α - коэффициент теплоотдачи;

К_1а,К_2а,К_3а - линейные коэффициенты зависимости температуропроводности от температуры;

K_1λ,K_2λ,K_3λ - линейные коэффициенты зависимости теплопроводности от температуры;

τ - текущее время, отсчитываемое от момента подачи импульса;

τ* - длительность теплового импульса;

ξ₁,ξ₂ - параметры регуляризации;

J - функционал невязки.

Сущность изобретения поясняется чертежами.

На фиг.1 представлена пространственная сетка (M,N,P) математической модели в плоскости (x,y,z).

На фиг.2 представлены относительные графики, аппроксимирующие зависимость: 1 - для температуропроводности в виде а(T)/а(0) при К_1а=-0,001·10^-3, K_2а=-0,01·10^-3;

K_3а=-0,05·10^-3; 2 - для теплопроводности в виде λ(T)/λ(0) при К_1λ=0,1·10^-3, K_2λ=4·10^-3, K_3λ=8·10^-3.

На фиг.3 приведен вариант определения теплофизических свойств исследуемого материала с минимально возможным значением невязки, где кривая 1 - график температуры, построенный математической моделью, кривая 2 - график температуры реального испытания, где τ₁ - время начала измерения температуры, отсчитываемое от момента подачи теплового импульса; τ₂ - время окончания измерения температуры, отсчитываемое от момента подачи теплового импульса; Δτ - шаг сетки по времени.

На фиг.4 показана схема устройства, реализующая предлагаемый способ определения комплекса ТФС твердых материалов.

Устройство (Фиг.4) содержит инфракрасный излучатель 1, инфракрасный измеритель температуры 2 и исследуемый материал 3.

Инфракрасный излучатель 1 в течение заданного времени τ* равномерно воздействует по всей площади поверхности исследуемого материала радиусом R, а с помощью инфракрасного измерителя температуры в интервале времени [τ₁,τ₂] ^B центре материала измеряют избыточные значения температур. Для соблюдения условия полуограниченности исследуемого материала толщиной Н необходимо, чтобы H/R≥20 (Карслоу Г., Егер Д. Теплопроводность твердых тел. - М.: Наука, 1964. - 114 с.).

Сущность изобретения заключается в следующем.

По всей площади плоской поверхности исследуемого образца 3 осуществляют тепловое импульсное воздействие источником тепла 1 (инфракрасным излучателем), формирующим лучистый тепловой поток известной плотности и длительности, при этом измеряют инфракрасным измерителем температуры 2 избыточную температуру в центре образца в заданном интервале времени [τ₁,τ₂] (фиг.3, фиг.4). Охлаждение поверхности осуществляется путем естественного конвективного теплообмена с окружающей средой. Для определения теплофизических свойств исследуемого материала используют математическую модель прямой задачи теплопроводности на основе метода конечных разностей (фиг.1), полученную решением нелинейной задачи теплопроводности с учетом теплоотдачи с окружающей средой:

где T_n - температура поверхности исследуемого образца; h (τ)- ступенчатая функция.

Нелинейную задачу теплопроводности (7) при граничных условиях (8) решают методом конечных разностей. Разностная схема для трехмерного уравнения теплопроводности имеет вид (3). Граничные условия аппроксимируют на основании выражения:

полученного с помощью метода теплового баланса. При этом q и α отнесены к единице площади поперечного сечения пространственной сетки и выражены в Вт/м² и Дж/(м²·К).

Выражение (9) приводят к виду (1), (2) и рассчитывают изменение значения избыточной температуры во времени в заданном интервале наблюдения избыточной температуры [τ₁,τ₂] с учетом зависимости температуропроводности и теплопроводности от температуры согласно кусочно-линейным функциям (4), (5).

Для расчета искомой сеточной функции «прогонками вдоль осей x,y,z», соответствующей температуре на k+1 временном слое, сначала применяют выражения (1), (2) при далее (3) при

Для получения при численном решении физически оправданных результатов следует соблюдать условие сходимости вычислений:

При минимальном значении функционала невязки значения избыточных температур, рассчитанные математической моделью и полученные при реальном испытании, совпадают с минимальной погрешностью, следовательно, значениям теплофизических свойств исследуемого материала ставятся в соответствие значения λ, и а математической модели (фиг.2, фиг.3). Расчет невязки с использованием дополнительных слагаемых и в формуле (6) позволяет достичь наилучшего приближения дискретной модели к экспериментальной термограмме, так как оно учитывает условие существования слабого экстремума. Решение задачи определения ТФС производится каким-либо из вариационных методов исчисления.

Результаты предварительных экспериментов показали, что при мощности теплового потока 150 Вт/м² и времени τ*=60 сек максимальное значение избыточной температуры для класса теплоизоляционных материалов составляет 50…120°C, что требует необходимость учета нелинейной зависимости изменения ТФС материла от температуры. Так с ростом температуры теплопроводность увеличивается, а температуропроводности уменьшается, а доля изменения ТФС может составлять до 10-30% на 100°С избыточной температуры, при этом наилучшая аппроксимация зависимости ТФС от температуры достигается параболической, экспоненциальной или кусочно-линейной функциями (Платунов Е.С. и др. Теплофизические измерения и приборы - Л.: Машиностроение, 1986).

Для обеспечения высокой воспроизводимости при каждом измерении на основании закона Ламберта угол наблюдения для металлов должен быть 0…40°, а для диэлектриков в интервале 0…60° (Инфракрасная термография. Основы, техника, применение: Пер. с франц. - М.: Мир, 1988. - С.47). Инфракрасный излучатель должен быть расположен параллельно исследуемым материалам строго на определенной высоте для обеспечения заданного значения мощности теплового потока.

Для учета возникновения вынужденной конвекции при проведении измерений в полевых условиях коэффициент теплоотдачи может быть записан как функция от скорости ветра (Справочник физических величин / Под ред. проф. Г.А.Рябинина. - СПб., Лениздат; Издательство «Союз», 2001. - С.99).

Применение предлагаемого способа позволяет повысить точность определения комплекса ТФС материалов по сравнению с прототипом за счет исключения составляющих частных погрешностей измерения расстояния от источника тепла до датчика температуры, теплофизических свойств материала эталона, а также за счет учета зависимости теплофизических свойств исследуемого материла от температуры в виде кусочно-линейных функций, более точно аппроксимирующих реальный физический процесс.

В связи с тем, что предлагаемый способ позволяет определять комплекс ТФС без использования материала эталона, на котором размещают линейный источник на фиксированном расстоянии от датчика температуры, а измерение температуры производят в любой точке в центре исследуемого материала, проведение теплофизических измерений упрощается.

Способ определения комплекса теплофизических свойств твердых материалов, включающий тепловое импульсное воздействие на плоскую поверхность исследуемого образца, измерение избыточной температуры на плоской поверхности образца с момента подачи теплового импульса в одной точке в заданном интервале времени, отличающийся тем, что тепловое импульсное воздействие на плоскую поверхность образца осуществляют лучистым тепловым потоком известной плотности и длительности, а измерение избыточной температуры с момента подачи теплового импульса проводят в центральной части нагреваемой поверхности образца, при этом регистрируют значение максимальной избыточной температуры и время ее достижения, используя математическую модель прямой задачи теплопроводности на основе метода конечных разностей, применяют промежуточную сеточную функцию источника нагрева излучением и конвективного теплообмена: , при τ≤τ*; , при τ>τ*,при , ;сеточную функцию, учитывающую теплоперенос по всему объему образца: ,при , , ;для учета нелинейной зависимости теплофизических свойств материала от температуры используют кусочно-линейные функции: решают обратную коэффициентную задачу теплопроводности вариационным методом на интервале наблюдения избыточной температуры [τ₁,τ₂], при выборе параметра регуляризации по невязке: ,искомые теплофизические свойства а, 1 находят из минимума функции Jξ(a,λ), где - сеточная функция;Т - избыточная температура, регистрируемая в эксперименте; - избыточная температура, рассчитанная математической моделью;T_max - максимальное значение избыточной температуры, регистрируемое в эксперименте; - максимальное значение избыточной температуры, рассчитанное математической моделью;Т₁ - избыточная температура, регистрируемая в момент времени τ₁,Т₂ - избыточная температура, регистрируемая в момент времени τ₂;τ_max - момент времени регистрации избыточной температуры Т_max; - момент времени, рассчитанный математической моделью и соответствующий температуре ;a - температуропроводность;λ - теплопроводность;m - номер отсчета по координате x, ;n - номер отсчета по координате y, ;p - номер отсчета по координате z, ,x, y, z - оси правой декартовой прямоугольной системы координат;k - номер отсчета по времени;h - шаг сетки по расстоянию;Δτ - шаг сетки по времени;q - плотность теплового потока;α - коэффициент теплоотдачи;K_1α, K_2α, K_3α - линейные коэффициенты зависимости температуропроводности от температуры;K_1λ, K_2λ, K_3λ - линейные коэффициенты зависимости теплопроводности от температуры;τ - текущее время, отсчитываемое от момента подачи импульса;τ* - длительность теплового импульса;ξ₁,ξ₂ - параметры регуляризации;J - функционал невязки.