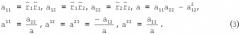Экспериментальный способ параметризации минимальных поверхностей со сложным контуром

Экспериментальный способ параметризации минимальных поверхностей со сложным контуром

Иллюстрации

Показать все

Реферат

Изобретение относится к отраслям, связанным с формированием поверхностей сложной геометрии и определением их метрики, в частности строительных конструкций, корпусов транспортных средств, космической техники, элементов приборов, дорожного покрытия и т.д.

Известны способы измерения горизонтальных неровностей (рихтовки) и кривизны в плане рельсовых нитей, заключающиеся в том, что измеряют текущий курс кузова путеизмерительного вагона и текущий угол виляния измерительной тележки относительно кузова. Далее измеряют расстояния от реборд соответствующих колес тележки до головок рельсов. По измерительной информации рассчитывают текущие курсы рельсовых нитей как текущий курс кузова минус текущий угол виляния измерительной тележки относительно кузова минус текущий угол непараллельности реборд колесных пар измерительной тележки и головок рельсовых нитей. Затем получают текущие значения горизонтальных неровностей рельсовых нитей как произведения базы тележки на отклонения текущих курсов рельсовых нитей от текущих усредненных на базе тележки курсов рельсовых нитей, рассчитанных от курсов рельсовых нитей (патент РФ №2276216, М.кл. Е01В 35/00, опубл. 10.05.2006).

Однако известные способы не позволяют формировать линии сложной геометрии и определять неровности двумерных объектов.

Известны способы определения кривизны и уклонов профиля поверхности дорожного покрытия в двух различных направлениях, включающие измерение параметров движения автомобиля, определение и корректировку базиса отсчета относительно плоскости, анализ упомянутых данных с помощью ЭВМ, нахождение уклонов дорожного покрытия в двух различных направлениях и выдачу на экран монитора измерительно-вычислительного комплекса расчетных параметров в процессе движения автомобиля (патент РФ №2114391, М.кл. G01C 7/04, опубл. 27.06.1998).

Однако известные способы не позволяют формировать поверхности сложной геометрии, в том числе минимальные поверхности заданной формы.

Известен также экспериментальный способ параметризации минимальных поверхностей, основанный на решении двухмерного уравнения Лапласа (на примере постановки внутренней задачи Дирихле, когда известны краевые значения координат и необходимо найти внутренние), в котором выставляют вертикальные стержни на необходимую высоту относительно опорной плоскости согласно требованиям задачи, с помощью измерительного прибора выверяют точность установки стержней, посредством фиксатора закрепляют стержни на необходимой высоте, натягивают на вертикальные стержни заранее изготовленную сеть из гибкого эластичного материала, с помощью высокоточного измерительного прибора замеряют высотные координаты во внутренних точках (точках пересечения) эластичной гибкой сети (патент РФ №2121166, М.кл. G09B 23/04, опубл. 27.10.1998).

Указанный способ обладает следующими недостатками:

а) способ не позволяет получать непрерывные и гладкие контуры произвольной конфигурации, свободно ориентированные в пространстве (все контуры имеют прерывистый дискретный характер);

б) способ предназначен только для измерения геометрических параметров объекта и не позволяет формировать минимальные поверхности со сложным контуром;

в) в способе не предусмотрено вычисление метрики поверхности (определение компонент первого и второго метрических тензоров);

г) координаты в горизонтальной плоскости имеют фиксированные значения (координаты установки вертикальных стержней не изменяемые).

Задачей (целью) изобретения является формирование поверхности с непрерывными и гладкими криволинейными координатными линиями, описание поверхности сложной геометрии, произвольно ориентированной в пространстве, и вычисление компонент первого и второго метрических тензоров (метрики поверхности).

Указанные задачи достигаются тем, что в экспериментальном способе параметризации минимальных поверхностей со сложным контуром, включающем операции фиксации гибкого элемента относительно основания, натягивания на него заранее изготовленной сети из эластичного материала, замера координат узловых точек сети относительно основания, изготавливают пространственный каркас из криволинейных формообразующих элементов (например, кусков гнущейся проволоки), образующих заданный четырехугольный контур, натягивают на каркас первоначально прямоугольную в плане сеть из эластичного материала, причем каждую узловую контурную точку сети закрепляют на соответствующих точках каркаса, распределенных по длине формообразующего элемента или равномерно, или по определенной заданной закономерности. Каркас с сетью фиксируют относительно опорной плоскости основания. При этом поверхность формируют и параметризируют по узловым точкам сети. Для этого замеряют координаты узловых точек сети относительно выбранной системы координат, связанной с опорной плоскостью. Выполняют обработку полученных результатов с определением компонент метрики поверхности.

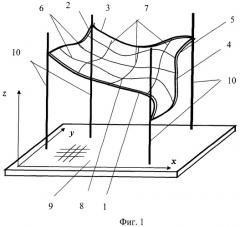
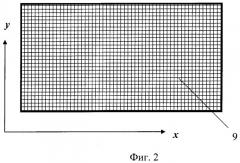
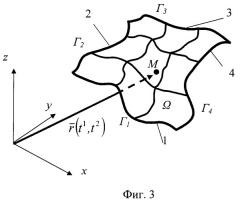
На фиг.1 схематически представлен общий вид установки для экспериментальной параметризации поверхности; на фиг.2 показаны вспомогательные координатные линии, нанесенные на поверхность основания; на фиг.3 представлен фрагмент формируемой поверхности при разбиении контура на заданное число точек; на фиг.4 изображена схема сети из эластичного материала в виде единичного квадрата, которая предназначена для совмещения с контуром изготовленного каркаса; на фиг.5 - трехмерное изображение исходной поверхности, формируемой сетью единичного квадрата при наложении на каркас со сложным контуром; на фиг.6 - трехмерное изображение полученной после построения поверхности со сложным контуром; на фиг.7 - трехмерное изображение полученной после построения поверхности первых производных по первому параметру; на фиг.8 - трехмерное изображение полученной после построения поверхности первых производных по второму параметру.

На фигурах обозначены:

х, у, z - координаты в декартовой системе;

Г₁, Г₂, Г₃, Г₄ - контурные линии формируемой поверхности (контуры каркаса);

Ω - область, которую занимает формируемая поверхность;

t¹, t² - координаты (параметры) единичного квадрата (верхние индексы 1 и 2 - индексы, показывающие направление координат);

Ω_ф - область, которую занимает единичный квадрат в координатах t¹, t² (параметры t¹ и t² изменяются в частном случае от 0 до 7);

М - произвольная точка на формируемой поверхности;

М_ф - точка на области Ω_ф, соответствующая произвольной точке М формируемой поверхности;

- радиус-вектор произвольной точки М на формируемой поверхности.

Способ осуществляют следующим образом.

Изготавливают пространственный каркас контура формируемой поверхности. При этом каркас составляют из четырех пространственных криволинейных формообразующих элементов 1, 2, 3 и 4 (например, кусков гнущейся проволоки) с нанесенными на них метками согласно заданным условиям. Концы формообразующих элементов 1, 2, 3 и 4 жестко стыкуют с образованием замкнутого четырехугольника заданной формы, являющегося контуром формируемой поверхности.

На полученный каркас натягивают эластичную сеть 5. Сеть 5 состоит из продольных 6 и поперечных 7 эластичных, например, резиновых нитей, которые первоначально в исходном состоянии (при недеформированном состоянии эластичной сети) образуют прямоугольные ячейки. Продольные 6 и поперечные 7 резиновые нити в местах пересечения скреплены друг с другом с образованием узловых точек 8. При теоретической обработке эластичную сеть 5 условно принимают за единичный квадрат с параметрами t¹ и t², изменяющимися от 0 до 7.

Прикрепляют наружные нити сети 5 к соответствующим частям 1, 2, 3 и 4 каркаса по отмеченным меткам (точкам), распределенным по длине формообразующего элемента или равномерно, или по определенной заданной закономерности. При этом узловые точки 8 сети 5 при деформации сети 5 определяют формируемую поверхность, то есть по узловым точкам 8 формируют поверхность.

Далее приступают к процедуре параметризации поверхности. Для этого каркас фиксируют на установке, содержащей опорную плоскость основания 9 с нанесенными на ней координатными линиями и опоры 10 для фиксации каркаса.

Затем с применением соответствующих инструментов (приборов) замеряют координаты узловых точек 8 деформированной сети 5 по осям х, у и z при соответствующих параметрах t¹, t² единичного квадрата с областью Ω_ф, то есть получают координаты x(t¹, t²), y(t¹, t²), z(t¹, t²) и определяют радиус-вектор в узлах сетки по формуле:

где , , - единичные орты в декартовой системе координат.

Данные могут быть представлены в виде таблиц.

Алгоритм построения поверхности и вычисления ее параметров осуществляется в следующей последовательности:

1. Строят одномерные эрмитовы сплайны вдоль координаты t¹ при фиксированном значении координаты t² для всех функций координат x(t¹, t²), y(t¹, t²), z(t¹, t²), последовательно пробегая по всем значениям, соответствующим продольным нитям (линиям) 6 сети 5.

2. Строят одномерные эрмитовы сплайны вдоль координаты t² при фиксированном значении координаты t¹ для функций x(t¹, t²), y(t¹, t²), z(t¹, t²), последовательно пробегая по всем значениям, соответствующим поперечным нитям (линиям) 7 сети 5.

Тем самым получают значения координат формируемой поверхности σ для любого значения параметров t¹ и t².

3. По значениям первых производных определяют вторые смешанные производные для функций координат x(t¹, t²), y(t¹, t²), z(t¹, t²).

4. Строят эрмитовы кубические сплайны для функций координат x(t¹, t²), y(t¹, t²), z(t¹, t²).

5. Дифференцируя выражение (1) по t¹ и t², определяют координатные векторы и :

6. Определяют ковариантные и контравариантные a¹¹, a¹², a²² компоненты первого основного метрического тензора и фундаментальный определитель a:

7. Определяют символы Кристоффеля второго рода , , , , , :

,

,

,

,

.

8. Определяют вектор единичной нормали :

который вместе с координатными векторами и образует основной базис в каждой конкретной точке области Ω, принадлежащей формируемой поверхности σ.

9. Определяют ковариантные компоненты b₁₁, b₁₂, b₂₂ и смешанные компоненты , , , второго основного метрического тензора:

, где ;

, где ;

, где ;

Таким образом, для формируемой поверхности получают значения координат и компоненты первых и вторых производных для любых значений параметров t¹ и t² единичного квадрата.

Далее полученные величины могут быть использованы при подборе необходимых поверхностей при поиске архитектором нужной формы, для расчета напряженно-деформированного состояния оболочек со срединной поверхностью σ и т.д.

Пример построения поверхности сложной геометрии.

Была построена экспериментальная модель по изложенному способу, представляющая собой квадратный в плане (с размерами 40 см на 40 см) каркас с криволинейными контурами. На каркас натянули сеть из эластичного материала с восьмью узловыми точками в обоих направлениях единичного квадрата. Таким образом, сеть имела разбиение по 7 ячеек по продольным и поперечным координатам. Каркас с сетью зафиксировали относительно опорной плоскости основания на четырех опорах, выполненных в виде вертикальных стержней.

На экспериментальной модели замерили координаты узловых точек. Значения замеренных координат z_ij для исследуемой формируемой поверхности сложной формы приведены в таблице.

Значения замеренных вертикальных координат z узловых точек для рассматриваемой сети по параметрам t1 и t2, см
Номера узловых точек по t2	Номера узловых точек по t1
1	2	3	4	5	6	7	8
1	16,8	16,8	14,8	10,3	4,0	0,004	0,0	0,0
2	14,6	13,5	12,0	9,5	6,5	4,7	4,3	4,1
3	12,2	11,3	10,1	8,8	7,5	7,2	7,1	6,5
4	9,6	9,6	9,0	8,2	8,2	8,2	8,7	8,4
5	7,7	7,8	8,0	8,2	8,4	8,8	9,6	10,2
6	5,6	5,8	6,5	8,1	9,6	11,2	12,0	12,6
7	3,0	3,5	4,7	7,6	9,9	12,6	13,5	14,7
8	0,0	0,0	0,0	4,8	11,6	15,4	16,8	16,8

После замеров координат x(t¹, t²), y(t¹, t²), z(t¹, t²) в узловых точках построили поверхность с использованием аппарат сплайн-функций по описанному способу и вычислили геометрические параметры сформированной поверхности. В частности, по вычисленным значениям были построены графические изображения некоторой поверхности. Например, на фиг.5 представлено изображение поверхности исходной геометрии, построенное на основе замеренных координат х, у и z. На фиг.6 показана геометрия фрагмента построенной поверхности, полученной с использованием изложенного алгоритма. На фиг.7 и 8 показаны поверхности первых производных по направлениям t¹ и t² соответственно.

Предложенный способ позволяет формировать поверхности сложной геометрии с непрерывными и гладкими криволинейными координатными линиями, произвести описание поверхностей сложной геометрии, произвольно ориентированной в пространстве, и вычислять компоненты первого и второго метрических тензоров (метрика поверхности). Способ позволяет получать непрерывные и гладкие контуры произвольной конфигурации, свободно ориентированные в пространстве, формировать минимальные поверхности со сложным контуром. Способ является эффективным средством решения самых разнообразных прикладных задач и может найти широкое применение в проектных организациях и учебных заведениях при проектировании и изучении различных поверхностей сложной геометрии, а также при расчетах напряженно-деформированного состояния тонкостенных конструкций сложной геометрии, когда на первом этапе необходимо решить задачу параметризации (задания) срединной поверхности сложной геометрии и вычислить соответствующие компоненты первого и второго метрических тензоров, символы Кристоффеля и т.д.

1. Экспериментальный способ параметризации минимальных поверхностей со сложным контуром, включающий операции фиксации гибкого элемента относительно основания, натягивания на него заранее изготовленной сети из эластичного материала, замера координат узловых точек сети относительно основания, отличающийся тем, что изготавливают пространственный каркас с четырехугольным контуром из криволинейных формообразующих элементов, натягивают на каркас первоначально прямоугольную в плане сеть из эластичного материала, причем каждую узловую контурную точку сети закрепляют на соответствующих точках каркаса, распределенных по длине формообразующего элемента по определенной закономерности, при этом поверхность формируют и параметризируют по узловым точкам сети с учетом координат узловых точек сети относительно выбранной системы координат, выполняют обработку полученных результатов с определением компонент метрики поверхности.

2. Экспериментальный способ параметризации минимальных поверхностей со сложным контуром по п.1, отличающийся тем, что пространственные криволинейные формообразующие элементы изготавливают из кусков гнущейся проволоки.

3. Экспериментальный способ параметризации минимальных поверхностей со сложным контуром по п.1 или 2, отличающийся тем, что точки крепления узловых контурных точек сети распределяют по длине формообразующего элемента равномерно.