Способ стеганографического сокрытия информации

Способ стеганографического сокрытия информации

Иллюстрации

Показать все

Реферат

Изобретение относится к области телекоммуникаций и предназначено для скрытой передачи секретной информации.

Известен способ стеганографического сокрытия информации [1, 2, 4, 8], заключающийся в том, что в графическом изображении заменяют младшие биты цветовых составляющих. При этом для сокрытия одного байта информации требуется 8 байт пространства в контейнере. Вложения, сделанные с помощью этого способа, легко обнаруживаются и могут быть подвергнуты криптоанализу.

Известен способ внедрения дополнительной информации в цифровые изображения [6]. Основная идея данного технического решения заключается в том, что фотореалистическое изображение разделяют на три цветовые составляющие (R, G, B). Далее выделяют биты одной составляющей, например R. Анализируют пары рядом стоящих битов. Если имеются пары 11 или 00, то их не используют для сокрытия информации. Если пары соседних битов образуют комбинации 10 или 01, то с их помощью скрывают информацию. В зависимости от передаваемой (скрываемой) информации кодер формирует комбинацию 10 или 01. При этом считается, что комбинация битов 10 соответствует скрываемой единице, а комбинация битов 01 - скрываемому нулю.

У данного изобретения есть существенный недостаток.

Вся информация помещается в единственный контейнер (в один файл), и так как алгоритм сокрытия известен, то выделить сообщение не представляет труда. По сути, этот способ сокрытия не является способом сокрытия (если смотреть на него с позиций закона Керкхоффа). При известном неизменном алгоритме шифрования сокрытия нет. В способе нет секретного ключа, который может затруднить стегоанализ.

Известен способ сокрытия информации [7], заключающийся в том, что в графическом изображении ищут области (так называемые «сигнатурные точки») с наибольшими и наименьшими значениями пикселей (относительные экстремумы) и используют найденные точки для сокрытия информации. Для выбора сигнатурных точек предлагается использовать метод разности средних.

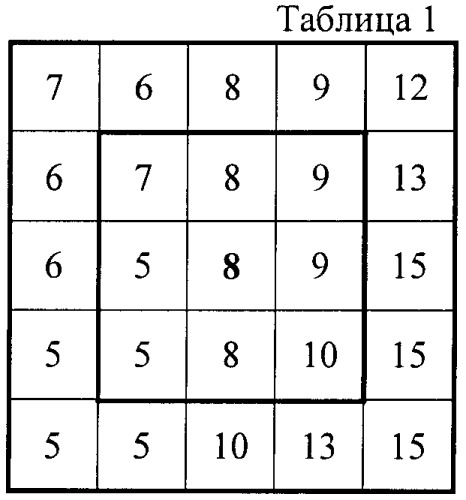
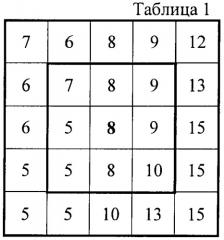
Расчет производится следующим образом. Сначала определяется среднее значение пикселей ближней окрестности (квадрат 3×3 с исследуемой точкой в центре). Затем вычисляется среднее значение пикселей большой окрестности (все точки квадрата 5×5 с исследуемой точкой в центре). Если проверяемая точка является относительным экстремумом, то в нее записывается секретная информация. Для внедрения информации значение найденного пикселя изменяется на незаметную для человеческого глаза величину. Пример одного из расчетов приведен в таблице 1.

Недостатком данного способа является то, что весь текст скрываемого сообщения находится в одном контейнере, и в случае удачи криптоаналитики могут взломать шифр.

Наиболее близким из аналогов (прототипом) является техническое решение, описанное в [5]. На стр.95 [5] написано, что стеганографические методы могут обеспечить высокий уровень защиты информации только в том случае, когда они будут дополнены предварительным криптографическим преобразованием сообщений (шифрованием). Причем последние будут определять реальную стойкость такой комбинированной секретной системы.

Открытый текст превращают в криптограмму, для чего его шифруют методами многоалфавитной замены (на ключе K1) и методом перестановок (на ключе К2), полученную криптограмму скрывают в графическом контейнере.

Таким образом, прототип предполагает наличие операций криптографического шифрования сообщения и стеганографического сокрытия полученной криптограммы.

У прототипа есть недостатки.

Зашифрованный текст скрывается в единственном контейнере. При удаче криптоаналитик может восстановить открытый текст, так как в его распоряжении находится целое (недробленое) сообщение.

Существующие методы криптоанализа (линейный криптоанализ, дифференциальный криптоанализ, силовой взлом…) в ряде случаев позволяют осуществить компрометацию криптограммы, которая зашифрована известными методами шифрования.

Техническим результатом данного изобретения является повышение криптостойкости и стеганостойкости. Изобретение позволяет создать практически равновероятную смесь двоичных чисел, распыленных по неизвестным для противника контейнерам, например цифровым фотографиям. Положительным свойством заявляемого способа является возможность передачи практически любого символа (включая математические символы, иероглифы, химические формулы). Изобретение позволяет регулировать криптостойкость и быстродействие шифрования за счет изменения размера графической матрицы, числа контейнеров, используемых способов перемешивания в графической матрице и их числа.

Сущность предлагаемого способа стеганографического сокрытия информации заключается в том, что открытый текст превращают в криптограмму, для чего его шифруют методами многоалфавитной замены (на ключе K1) и методом перестановок (на ключе К2), полученную криптограмму скрывают в графическом контейнере, при этом изображение каждого символа полученной криптограммы формируют с помощью графической матрицы размером n×m в цифровой форме из w информативных точек, по периметру графической матрицы формируют штрихпунктирную рамку, состоящую из r пограничных точек, и по всему полю изображения наносят q маскирующих точек, числа u=w+r+q для всех графических матриц выбирают одинаковыми, размер графической матрицы, порядок расположения информативных точек, пограничных точек в рамке и маскирующих точек определяют с помощью ключа К3, затем производят перемешивание точек в каждой графической матрице в соответствии с ключом K4, после этого берут t=s+d+f графических или иных контейнеров и информацию из перемешанных графических матриц в соответствии с ключом K5 побитно распыляют по s контейнерам, в d контейнеров помещают ложную информацию, а f контейнеров оставляют пустыми.

Описанный способ может иметь несколько модификаций.

В зависимости от ключа К3 используют разную конфигурацию шрифта (разные гарнитуры для изображения одной и той же буквы, разные стили: курсив, полужирный; формируют негативный шрифт, транспонируют матрицу, символы в графической матрице пишут с поворотом на угол 0≤j≤360 градусов, одинаковые буквы рисуют разной величины).

В зависимости от ключа К3 во время передачи одного закрытого сообщения форму графической матрицы регулярно изменяют, например после передачи каждых ста символов изменяют размер графической матрицы.

В зависимости от ключа К3 символы в графической матрице формируют из точек, псевдослучайным образом распыленных по матрице, каждому символу ставят в соответствие определенную псевдослучайную матрицу точек, число черных точек выбирают равным половине всех точек графической матрицы u=(n×m)/2.

В зависимости от ключа К4 перемешивание точек в графической матрице осуществляют псевдослучайной перестановкой строк и столбцов.

В зависимости от ключа К4 перемешивание точек в графической матрице осуществляют циклическим сдвигом содержимого столбцов и строк.

В зависимости от ключа К4 перемешивание точек в графической матрице осуществляют псевдослучайной перестановкой ячеек матрицы.

В зависимости от ключа К4 перемешивание точек в графической матрице осуществляют путем формирования групп пикселей в строке и перестановкой соседних групп.

В зависимости от ключа К4 перемешивание точек в графической матрице осуществляют путем формирования групп пикселей в столбце и перестановкой соседних групп.

В зависимости от ключа К4 преобразование графической матрицы осуществляют с помощью схемы Фейстеля.

В зависимости от ключа К4 преобразование графической матрицы осуществляют методом гаммирования, причем ключ К4 определяет состав гаммы.

В зависимости от ключа К4 перемешивание пикселей в графической матрице осуществляют путем комбинации различных операций (циклические сдвиги по строкам и столбцам, перестановка строк и столбцов, перестановка пикселей по случайному закону, с помощью схемы Фейстеля, перестановками групп, вращением строк и столбцов, методом гаммирования).

В зависимости от ключа К6 объединяют несколько графических матриц и выполняют перемешивание точек всего многопиксельного экрана.

Основная идея заявляемого технического решения заключается в следующем.

Для шифрования передаваемой информации текст представляют в виде множества графических матриц, состоящих из белых и черных точек. Точки в графических матрицах переставляются или заменяются другими в соответствии с выбранным ключом. Зашифрованная информация дробится на биты, которые распыляются по множеству графических или иных контейнеров (файлов).

Одним из применений изобретения является скрытная передача информации с помощью сайта, содержащего большое число фотографий (или Web-страниц). При этом противник не знает, какие фотографии являются контейнерами и в какой последовательности передаваемая информация распылена по контейнерам.

Для формирования практически равновероятной смеси битовых последовательностей изображения символов формируются из одинакового числа белых и черных пикселей. Это позволяет формировать на выходе шифратора последовательность двоичных сигналов с равномерным распределением.

Значительно усложняет стегоанализ распыление имеющейся битовой последовательности по нескольким контейнерам. Причем распыление происходит не детерминировано, а по псевдослучайному закону в соответствии с секретным ключом.

Необходимо отметить следующий момент, касающийся криптоанализа.

Многие методы криптоанализа основаны на создании модели открытого текста (учет повторения отдельных символов, создание таблиц частот встречающихся отдельных символов, биграмм, триграмм…). Автоматический криптоанализ предполагает использование цепей Маркова. В результате автомат, а не человек определяет: получен открытый текст или он ещё нечитаемый.

Однако модель К.Шеннона трудно применить для взлома сообщения, зашифрованного с помощью заявляемого способа. Символы здесь представлены с помощью графических матриц, и для силового взлома криптограммы следует использовать автомат распознавания образов. Задача становится принципиально неразрешимой, когда вместо традиционных символов используются графические матрицы с равновероятным распылением белых и черных точек.

Наибольшая степень защиты достигается в том случае, когда вместо символов, даже слегка напоминающих символы открытого текста, используется пёстрая, псевдослучайная мозаика. Автомат не будет знать, что искать. Лишь при утечке сведений о таблице (компрометации), которая связывает символы открытого текста и секретные псевдослучайные графические матрицы, появляется возможность произвести автоматический криптоанализ.

Но для полного криптоанализа потребуется преодолеть еще несколько уровней защиты.

Первый уровень - это традиционная криптографическая защита (сообщение должно быть предварительно зашифровано одним из распространенных, классических способов). Второй уровень - нужно определить размер графической матрицы, порядок расположения информативных, маскирующих, пограничных пикселей. Затем нужно определить, какой вид преобразования матрицы осуществлен в данном случае (сдвиг влево - вправо, вверх - вниз, перестановка столбцов, строк…) и каковы количественные характеристики этого преобразования. Третий уровень защиты состоит в решении комбинационной задачи по собиранию битов из пространственно распределенных контейнеров. При этом неизвестно, какие контейнеры содержат информацию и в какой последовательности распылены биты.

Осуществление изобретения.

Рассмотрим примеры формирования изображения различных символов с помощью графических матриц (см. фиг.1).

В данном случае выбрана матрица 8×8.

Следующая матрица имеет большее число пикселей: 10×10 (см. фиг.2).

Анализ приведенных изображений показывает, что для формирования разных символов требуется разное число информативных пикселей. Буква «Щ» содержит 29 черных точек, буква «Б» - 23, буква «Г» - 12, буква «Ж» - 24. Понятно, что такое заметное количественное различие графических матриц дает некоторую зацепку для криптоаналатиков. Например, они могут попытаться восстановить передаваемые символы путем подсчета числа пикселей в каждой графической матрице.

Улучшить ситуацию можно за счет формирования рамки вокруг изображения символов (фиг.3). При этом общее число черных точек во всех графических матрицах должно быть одинаковым. В случае необходимости, кроме рамки, вводят маскирующие точки. Благодаря такому дополнению число черных и белых пикселей (или единиц и нулей) во всех матрицах делают одинаковыми. Равенство белых и черных пикселей приводит к возникновению наибольшего хаоса (наибольшей энтропии).

Понятно, что полученные выше изображения символов все еще легко узнаваемы (распознаваемы). По этой причине сформированные графические матрицы с изображением символов необходимо трансформировать путем перемешивания пикселей. Перемешивание пикселей можно реализовать большим числом различных способов. Например, можно менять местами группы пикселей, расположенных в одной строке. Для этого все пиксели разбивают на группы по одному (два, три, четыре…) пикселя и соседние группы меняют местами. Такой же обмен можно произвести по столбцам. Естественно, что менять местами можно не только соседние группы, но и выбрать более сложный алгоритм.

Перемешивание можно осуществить перестановкой строк и столбцов. Эффективным средством перемешивания пикселей являются циклические сдвиги (например, влево для строк и вниз для столбцов).

Мощным инструментом изменения вида графической матрицы является генерация псевдослучайных целых чисел в диапазоне от 1 до n×m. Здесь n - число строк в матрице, a m - число столбцов. Случайные числа используются для определения порядка перемещения пикселей из исходной матрицы в перемешанную матрицу.

Изменить вид матрицы (трансформировать, преобразовать её) можно не только методами перестановки пикселей, но и методами замены. Для этого достаточно выполнить операцию ИКЛЮЧАЮЩЕЕ ИЛИ, взяв некоторую псевдослучайную последовательность чисел (гамму). Метод замены пикселей в графической матрице можно реализовать с помощью схемы Фейстеля.

На следующем чертеже (фиг.4) показан пример перестановки столбцов в графической матрице. Для упрощения картинки показаны заполненными только четыре столбца. Перестановка столбцов в исходной матрице (изображена сверху) происходит по ключу: 3-4-1-2… В результате получается «перемешанная» матрица (показана снизу).

Следующий чертеж (фиг.5) иллюстрирует процедуру перестановок строк по ключу: 3-1-4-2… Исходная графическая матрица показана слева, а "перемешанная" графическая матрица - справа.

Еще один чертеж (фиг.6) иллюстрирует процесс перемешивание точек (пикселей) с помощью операции циклического сдвига влево. Можно использовать и сдвиг вправо, но принципиальных отличий этих двух видов сдвига нет. Слово «циклический» означает, что столбцы 1 и 12 являются как бы соседними (смежными).

Операцию сдвига удобно технически реализовать с помощью сдвиговых регистров. При этом каждая ячейка матрицы соответствует отдельному триггеру. Повысить быстродействие устройств для реализации операций сдвига можно с помощью переключаемых сетей [5].

Результат циклического сдвига можно наглядно увидеть в строке 3. Исходная графическая матрица изображена слева. Результат перемешивание показан в матрице справа. Содержимое строки 3 сдвинуто циклически влево на 4 позиции.

Более простой вид циклического сдвига показан в строке 10. Здесь содержимое сдвинуто на две позиции влево. В этом случае не было перехода от первого столбца к двенадцатому, поэтому можно сказать: осуществлен сдвиг влево (слово «циклический» в этом случае можно опустить).

Рассмотрим, как осуществляется циклический сдвиг содержимого столбцов вниз. Так же, как и при сдвиге строк, можно осуществлять сдвиг содержимого столбцов вверх. Принципиального отличия нет. Для всех видов сдвига (влево - вправо и вверх вниз) криптоскойкость будет зависеть только от величины сдвига. Другими словами: изменяя значение ключа, можно перейти от сдвига влево к сдвигу вправо и от сдвига вниз к сдвигу вверх.

Конечно, правильнее говорить: «циклический сдвиг содержимого столбцов». Однако иногда будем говорить неправильно, но короче: «циклический сдвиг столбцов».

Исходная графическая матрица показана слева, а перемешанная матрица - справа (фиг.7).

Содержимое столбцов 2 и 9 сдвинуто циклически вниз на 2 позиции.

Рассмотрим еще один способ перемешивания (перестановок) пикселей в графической матрице (фиг.8).

Пронумеруем последовательно все ячейки графической матрицы слева направо и сверху вниз (традиционная траектория письма для европейской письменности). Для упрощения изложения идеи заполним числами только четыре строки. Ячейки второй графической матрицы пронумеруем с помощью псевдослучайных чисел (для еще большего упрощения изложения идеи пронумеруем только две строки правой матрицы).

Будем переносить содержимое левой матрицы в правую матрицу в следующем порядке. В ячейку 1-1 (первым указывается номер строки, а вторым - номер столбца) правой матрицы занесем содержимое ячейки 3-8 левой матрицы (эта ячейка отмечена числом 32). В ячейку 1-2 правой матрицы поместим содержимое ячейки 2-12 левой матрицы и т.д.

Возьмем конкретную матрицу и выполним указанные перестановки (32-24-7-15-35…). Результат показан на следующем чертеже (фиг.9).

Итак, перестановки в графической матрице осуществлены в соответствии со следующим фрагментом ключа:

32-24-7-15-35-47-5-13-29-8-40-33-1-45-2-16-27-31-42-11-23-37-41-3.

Необходимо ещё раз обратить внимание на то, что здесь рассмотрен лишь упрощенный вариант перестановок. Фактически ключ должен содержать в данном случае 144 натуральных числа, расположенных в псевдослучайном порядке (сгенерированных генератором случайных чисел).

Рассмотрим порядок перемешивания пикселей путем перестановки соседних групп пикселей. Для примера возьмем две графические матрицы 8×8 (фиг.10).

Образуем группы пикселей, объединив попарно соседние столбцы (фиг.11).

Выполним перестановки соседних групп. Перемещения будем вести построчно. Пиксель 1-1 перейдет в ячейку 1-3, пиксель 1-2 - в ячейку 1-4. Содержимое ячеек 1-3 и 1-4 перейдет соответственно в ячейки 1-1 и 1-2. В результате перестановок всех групп матрица будет иметь следующий вид (фиг.12).

Затем, объединив попарно строки, выполним перестановку групп пикселей в столбцах (фиг.13).

Рассмотрим пример перемешивания пикселей для графической матрицы с изображением русской буквы «Э». Перемешивание осуществим с помощью операций циклического сдвига и перестановок строк и столбцов (фиг.14).

Вокруг изображения выбранного символа, состоящего из w=16 пикселей, разместим рамку, состоящую из r=46 (двойная штрихпунктирная рамка). Кроме того, нанесем q=10 маскирующих точек. Общее число черных точек (пикселей) равно 72, то есть равно половине всех пикселей графической матрицы. Пиксели на приведенных чертежах имеют разный цвет. Естественно, это сделано лишь для наглядности. В конечном итоге каждый пиксель кодируется единицей или нулем, у которых, очевидно, не может быть цветовых оттенков. В дальнейшем сохраним лишь цвет для информативных пикселей, а маскирующие и пограничные (рамочные) пиксели будем обозначать одним цветом.

На следующем этапе шифрования информации необходимо перемешать пиксели в графической матрице.

В матрице, изображенной слева (фиг.15), произведена перестановка пикселей с помощью циклического сдвига строк влево в соответствии со следующим ключом:

3-4-7-5-5-3-6-11-2-5-4-6.

Ключ состоит из двенадцати чисел, которые определяют величину сдвига в каждой строке. Числа могут изменяться в диапазоне от 0 до 11.

Приведенные числа в ключе нужно понимать так: содержимое первой строки циклически сдвигается влево на 3 позиции, содержимое второй строки циклически сдвигается влево на 4 позиции, содержимое третьей строки циклически сдвигается влево на 7 позиций и т.д.

Затем матрица претерпевает дальнейшее преобразование (фиг.15). Пиксели переставляются путем циклического сдвига столбцов вниз в соответствии с ключом

2-5-1-4-4-6-10-3-4-5-5.

Эти числа следует понимать так: содержимое первого столбца циклически смещается на 2 позиции вниз, содержимое второго столбца циклически смещается на 5 позиций вниз и т.д.

Дальнейшее перемешивание пикселей происходит путем перестановки столбцов в соответствии с ключом (фиг.16)

5-8-2-10-3-1-12-9-4-6-7-11.

Этот ключ обязательно содержит все числа от 1 до 12 включительно и определяет порядок перестановки столбцов.

Так, содержимое столбца 5 исходной матрицы переписывается в новую матрицу в ячейки первого столбца. Столбец 8 переносится на место столбца 2, столбец 2 исходной матрицы записывается в третий столбец новой матрицы и т.д. Программно реализация перестановок осуществляется с помощью математических матриц.

Последняя операция перемешивания пикселей в рассматриваемом примере - это перестановка строк в соответствии с ключом (фиг.16)

9-3-5-7-2-1-11-12-10-4-6-8.

Приведенные числа нужно понимать так: в новой матрице в первый столбец записывается содержимое столбца 9 исходной матрицы, во второй столбец переносится содержимое столбца 3 и т.д.

Рассмотрим, как можно трансформировать исходную графическую матрицу методом замены (методом гаммирования). Преобразование матриц осуществим путем суммирования по правилу ИСКЛЮЧАЮЩЕЕ ИЛИ содержимого строк и двоичной гаммы.

Выберем следующий алгоритм преобразований: нечетные строки будем поразрядно (побитно) суммировать с числом 10100110, а четные строки суммировать с двоичным числом 00011011. Другими словами: гамма состоит из шестнадцати двоичных чисел, которые периодически (четырежды) повторяются.

Результат преобразования матриц показан под изображением символов (фиг.17). Справа показаны две матрицы, которые являются разностями между изображениями исходных матриц и изображениями преобразованных матриц. Как видно из чертежей, разностные матрицы одинаковы. Это может дать зацепку для криптоаналитиков.

Легко заметить, что в первой и восьмой строках преобразованных матриц присутствует в чистом виде секретная гамма.

Приведенный пример показывает, что преобразование графической матрицы можно осуществлять методом гаммирования. Однако следует строго выполнять рекомендации теории: период гаммы должен быть достаточно большой, и распределение единиц и нулей должно быть равномерным.

Наглядным примером влияния качества гаммы на криптостойкость являются следующие факты. Если гамма состоит из одних нулей, то исходная матрица не изменяется. Если гамма состоит только из единиц, то получается негатив (на фиг.18 показан негатив буквы «Ч».) Поэтому всякое отклонение от равномерного распределения битов гаммы увеличивает шансы криптоаналитиков по взлому шифра.

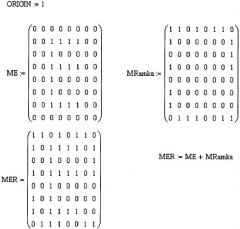
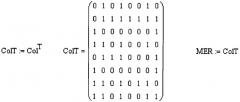
Описанные преобразования удобно комментировать, используя математические понятия: матрица, вектор-строка, вектор-столбец. С помощью матрицы ME представим букву «Е». С помощью матрицы MRamka сформируем изображение рамки, которое обрамляет изображение символа. Следующий пример реализован с помощью математической системы Mathcad.

Графическое представление матриц с изображением буквы «Е» и рамки дано на следующих чертежах (фиг.19).

Просуммируем матрицы ME и MRamka. Изображение символа с рамкой по периметру показано на следующих двух чертежах (фиг.20).

Чертеж слева (фиг.20) показывает трехмерное изображение символа с нанесенной рамкой. На чертеже справа верхний слой отображает единичные элементы матрицы, а нижний слой - нулевые элементы.

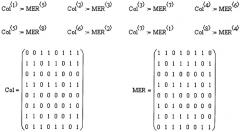
Осуществим перестановку вектор-столбцов матрицы MER в соответствии с ключом

5-3-7-6-8-2-1-4.

В матрице Col осуществлена перестановка столбцов в соответствии с указанным ключом.

На чертежах (фиг.21) показаны исходная матрица MER и перемешанная матрица Col.

Для перестановки строк сначала выполним транспонирование матрицы Col (таковы особенности математической системы Mathcad).

Теперь произведем перестановку строк в соответствии с ключом

2-4-1-8-5-7-6-3.

Выполним обратное транспонирование матрицы.

В матрице Row по отношению к исходной матрице MER выполнены перестановки столбцов и строк в соответствии с указанными ключами (фиг.22). На чертеже справа совместно изображены исходная и перемешанная матрицы.

Рассмотрим, как выполнить преобразование графической матрицы с помощью схемы Фейстеля [5]. Схема показана на фиг.23.

Принцип работы этой схемы рассмотрим на примере преобразования одной строки. Схема состоит из двух шифраторов F1 и F2, двух сумматоров по модулю два M1 и М2 (выполняют логическую операцию ИСКЛЮЧАЮЩЕЕ ИЛИ). Результаты шифрования (С1 и С3) зависят от алгоритма работы шифраторов F1 и F2 и ключей К1 и К2 соответственно. Для определенности будем считать, что и в шифраторах также реализуется логическая операция ИСКЛЮЧАЮЩЕЕ ИЛИ.

Исходная строка АВ делится на два равных блока А и В (по четыре бита). Результаты преобразований приведены в таблице 2.

Аналогичные преобразования делают с содержимым всех строк исходной графической матрицы.

В заявляемом изобретении криптостойкость обеспечивается несколькими уровнями защиты.

На первом уровне открытый текст шифруется одним и несколькими известными способами. На втором уровне защиты символы криптограммы заменяются графическими матрицами, в которых осуществляется перестановка или замена всех пикселей. На третьем уровне пиксели из перемешанных матриц побитно псевдослучайно распыляются по нескольким контейнерам. На четвертом уровне защиты рассредоточение заносимых битов происходит не линейно (не последовательно), а, например, равномерно по всей графической картинке контейнера. Другими словами: адреса цветовых составляющих в графическом файле выбирают по сложному закону. Закон распределения пикселей по графическому контейнеру удобно выразить с помощью математической зависимости. Коэффициенты в этой зависимости должны храниться в виде ключа.

Предположим, что криптоаналитику каким-то способом удалось преодолеть все уровни защиты, кроме восстановления графической матрицы.

При криптоанализе методом перебора всех возможных ключей восстанавливаемые матрицы придется анализировать с помощью автоматических устройств. Устройство распознавания образов должно во множестве точек графической матрицы мгновенно увидеть (выделить) замаскированный символ. Однако появление даже нескольких маскирующих точек приводят к снижению надежности автоматического распознавания символов.

Эту мысль иллюстрирует чертеж (фиг.24), полученный при работе программы FineReader 6.0 Professional. Три группы символов «ЧПРС» были в разной степени зашумлены маскирующими точками. По мере увеличения числа маскирующих точек результаты распознавания ухудшались. Чертеж показывает, что добавление всего девяти новых точек исказило все четыре буквы исходного текста. Размещение вокруг символов штрихпунктирных рамок делает текст полностью нечитаемым для автоматических устройств. Криптографическое перемешивание пикселей в графических матрицах ставит автомат в тупик.

Участие человека при криптоанализе в качестве распознавателя образов практически невозможно из-за необходимости перебора и анализа огромного числа вариантов в короткий промежуток времени.

Естественно, что рассмотренная программа распознавания символов не самая совершенная среди существующих программ этого класса. Однако во всех случаях криптоанализа возникает достаточно сложная проблема автоматического распознавания сложных образов.

Рассмотрим ещё один способ перемешивания пикселей. Для реализации предлагаемой идеи нужно рядом разместить четное число графических матриц (2, 4, 6, 8 и т.д.). Рядом размещенные графические матрицы должны образовать прямоугольную таблицу (многопиксельный экран) с общими столбцами и строками. Затем производят операции перемешивания с экраном так, будто бы это единая графическая матрица.

Рассмотрим пример. Предположим, что даны четыре графические матрицы с изображениями букв Щ, Б, Г и Ж. Информативные пиксели для повышения наглядности выделим отличающимся цветом (фиг.25).

Сдвинем циклически все строки, начиная со второй, на 1, 2, 3, 4, 5 и т.д. позиций влево. Естественно, что в реальных системах данный ключ должен выбираться по псевдослучайному закону (в данном случае регулярный ключ выбран для лучшей наглядности). В результате будет получен новый (перемешанный) экран (фиг.26).

После этого аналогично делаются циклические сдвиги столбцов всего экрана.

Теперь рассмотрим, каким образом зашифрованная (например, перемешанная) с помощью матриц информация распыляется по пространственно распределенным контейнерам.

Сообщение, последовательно внедренное в изображение с помощью существующих методов стеганографии, может быть обнаружено как визуально (после предварительной обработки изображения-контейнера) [4], так и с помощью статистических методов.

Рассмотрим принцип действия программы showlt, предназначенной для проведения визуальной атаки на графический стеганографический контейнер формата BMP. Для обнаружения скрытого вложения на базе имеющегося графического контейнера создается новое изображение в соответствии со следующим алгоритмом.

Если младший бит байта цветовой компоненты пикселя исследуемого контейнера содержит единицу, то во все биты этого байта записываются единицы. Аналогично, если младший бит байта цветовой компоненты пикселя исследуемого контейнера содержит нуль, то во все биты байта соответствующей цветовой компоненты пикселя записываются нули (фиг.27). На предыдущем чертеже (а) представлен пример однотонного (черного) контейнера.

Без специальных мер визуально обнаружить наличие вложения практически невозможно. Однако после описанной выше обработки контейнера (проявления) следы внедрения текста в графическое изображение отчетливо видны (фиг.27б).

Чертеж (фиг.27б) показывает, что тайное вложение заполняет контейнер наполовину. Локализация (определение местоположения) секретного вложения дает возможность злоумышленнику извлечь вложение и попытаться восстановить текст. Атака также может быть направлена на удаление (или искажение) сообщения, что в данном случае является тривиальной задачей. Визуальная атака с целью обнаружения скрытого вложения особенно эффективна при использовании в качестве контейнеров однородных компьютерных изображений, таких как схемы, графики, планы и т.п. На таких рисунках существенная часть изображения заполнена одинаковыми цветовыми составляющими (имеет одинаковый цвет).

Одним из методов повышения стеганографической стойкости является распыление (распределение) элементов сообщения по всей площади графического изображения. Однако в случае перехвата сообщения нарушитель получает возможность произвести анализ содержимого единого контейнера и при удаче получить открытый текст.

Другой подход к повышению секретности - распыление сообщения по нескольким контейнерам. Этот подход рассматривается в данной заявке.

Перед внедрением сообщение разбивается на k блоков (частей). Затем выбирается ключ, состоящий из k натуральных чисел. Ключ определяет порядок внедрения блоков секретного сообщения в распределенные контейнеры. После сокрытия текста контейнеры передаются по одному или нескольким открытым каналам связи. При этом некоторые контейнеры могут быть пустыми, а некоторые контейнеры могут содержать дезинформацию (шум). На приемной стороне производится извлечение блоков секретного послания в порядке, который определен секретным ключом. Если противнику удастся перехватить (скачать, получить) отдельный контейнер, то это не позволит ему восстановить сообщение в полном объеме.

Рассмотрим пример.

Разобьём секретный текст на блоки, состоящие из одной буквы (символа). Скроем блоки текста в графических контейнерах. Для упрощения изложения используем запись данных в наименее значащий бит цветовых компонент изображения в формате BMP. Предположим, что для внедрения выбрано 4 отдельных контейнера (например, изображения в формате BMP). Пусть требуется передать секретный текст - «УДАР», выбранный ключ является последовательностью чисел: 4, 2, 1, 3.

Вначале нужно разбить секретное сообщение на блоки. Разделим текст на четыре блока (символа): «У», «Д», «А», «Р». В соответствии с ключом блок «У» будет записан в контейнер с номером 4, блок «Д» - в контейнер с номером 2, блок «А» - в контейнер с номером 1 и, наконец, блок «Р» будет скрыт в контейнере с номером 3. На следующем чертеже (фиг.28) представлена часть дампа файла BMP до внедрения блока сообщения.

Нетрудно заметить, что данные изображения, начинающиеся со смещения 36Н, содержат нулевые байты. Это означает, что исходное изображение является прямоугольником черного цвета. На следующем чертеже (фиг.29) показана часть дампа того же файла после внедрения блока секретной информации.

Из чертежа видно, что байты, начиная со смещения 36Н, подверглись изменению и хранят теперь двоичный код буквы «У» (11010011). Аналогичным образом скрываются и другие части секретного послания.

Процесс распределения информации в пространстве можно представить в виде простой схемы (см. фиг.30).

На приемной стороне с помощью ключа восстанавливается необходимая последовательность извлечения блоков секретной информации из распределенных контейнеров: 4, 2, 1, 3. Первый блок извлекается из контейнера под номером 4. После этого обрабатывается контейнер под номером 2 и т.д. Наконец, извлеченные блоки соединяются, образуя читаемый текст: «У»+«Д»+«А»+«Р»=«УДАР».

Если злоумышленник перехватит один или несколько контейнеров, то он будет обладать не всей информацией, а только лишь ее частью. Если же перехвачены будут все отдельные контейнеры, то нарушителю предстоит решить задачу восстановления верной последовательности блоков (символов) секретной информации. Ещё больше осложнить криптоанализ можно за счет введения ложных контейнеров, которые будут содержать дезинформацию (шум). На приемной стороне ложные контейнеры будут отброшены, так как известен ключ распыления информации.

Заметим, что исходная информация, естественно, должна быть предварительно зашифрована одним из криптографических способов. Другими словами: в распределенные контейнеры помещается не открытый текст, а криптограмма. Распределение информации в пространстве создает еще один уровень защиты.

Дальнейшее совершенствование метода пространственного распыления информации сводится к побитному распределению информации по контейнерам. В этом случае каждый отдельный контейнер не будет содержать ни одного полного (цельного, единого) байта скрываемого текста.

Рассмотрим побитное распределение информации на примере. В качестве исходных данных возьмем условия предыдущего примера.

Сначала представим секретный текст в двоичной форме, используя таблицу CP1251 (таблица 3).

Таблица 3
Символ	Десятичный ANSI-код	Двоичный ANSI-код
У	211	11010011
Д	196	11000100
А	192	11000000
Р	208	11010000

Следующий шаг - генерация последовательности выбора контейнеров на основе ключа. Для ключа «СЕКРЕТ» получаем: 1, 3, 2, 2, 4, 1, 1, 3; 3, 3, 1, 1, 4, 3, 2, 4; 1, 3, 3, 3, 1, 3, 1, 3; 1, 4, 4, 1, 2, 2, 2, 1. Биты текста внедряются последовательно от старших разрядов к младшим. Порядок внедрения бит первого символа секретного текста показан на фиг.31.

При использовании такого способа сокрытия информации биты сообщения претерпевают дополнительную псевдослучайную перестановку, что увеличивает криптографическую стойкость сообщения. Вместе с тем ни один из отдельных контейнеров не содержит инфор