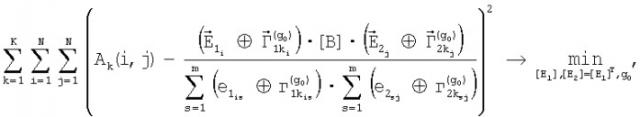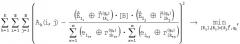Способ сжатия и восстановления сообщений

Способ сжатия и восстановления сообщений

Иллюстрации

Показать все

Реферат

Изобретение относится к области электросвязи, а именно к методам обработки данных с сокращением избыточности передаваемой информации. Предлагаемый способ может быть использован для передачи неподвижных изображений по цифровым каналам связи и относится к классу способов кодирования-восстановления на основе преобразования.

Известны способы кодирования изображений на основе импульсно-кодовой модуляции, дифференциальной импульсно-кодовой модуляции, статистического кодирования и кодирования с предсказанием, см., например, книгу: У.Претт. Цифровая обработка изображений. Часть 2. - М.: Мир, 1982, с.641-688. Данные способы подразумевают кодирование изображений с поэлементной обработкой, когда непрерывный видеосигнал преобразуется в последовательность квантованных отсчетов и затем представляется кодовыми словами в виде нулей и единиц.

Известны также способы кодирования на основе преобразования, см., например, книгу: Н.Ахмед, К.Р.Рао. Ортогональные преобразования при обработке цифровых сигналов. - М.: Радио и связь, 1980, с.192-201. Данные способы включают выполнение трех операций: сначала изображение подвергается двумерному ортогональному преобразованию, полученные в результате коэффициенты преобразования квантуются и в дальнейшем кодируются для передачи по каналу связи.

Недостатком перечисленных выше способов-аналогов является относительно высокая требуемая скорость передачи информации по цифровому каналу связи при заданном качестве восстановления сообщений.

Наиболее близким по своей технической сущности к заявленному способу сжатия и восстановления сообщений является способ, описанный в патенте России RU №2246798 С1, МПК H04N 7/30 от 20.02.2005 г.

Известный способ-прототип заключается в том, что предварительно идентично до начала сеанса связи на передающей и приемной сторонах генерируют случайную квадратную матрицу размером m×m элементов, каждый элемент которой принадлежит диапазону от -500 до 500, и по К>1 случайных ключевых матриц размерами N×m и m×N единичных и нулевых элементов формируют нормировочную матрицу размером N×N элементов, элементы которой C(i,j) вычисляют по формуле C(i,j)=(i+j)/(2×M), где i=1,2,…, N, j=1,2,…, N. Далее при ведении сеанса связи на передающей стороне К матриц квантованных отсчетов неподвижного полутонового изображения размером М×М элементов представляют в виде К матриц нормированных значений размером N×N элементов. Для этого формируют К матриц коэффициентов двумерного дискретно-косинусного преобразования размером М×М элементов путем последовательного перемножения матрицы дискретно-косинусного преобразования размером М×М элементов на каждую матрицу квантованных отсчетов неподвижного полутонового изображения размером М×М элементов и на транспонированную матрицу дискретно-косинусного преобразования размером М×М элементов, формируют К матриц коэффициентов двумерного дискретно-косинусного преобразования размером N×N элементов по формуле Z_k(i,j)=H_k(i,j), где i=1,2,…, N, j=1,2,…, N, k=1,2,…, K, H_k(ij) - ij-й. элемент k-й матрицы коэффициентов двумерного дискретного косинусного преобразования размером М×М элементов, Z_k(i,j) - ij-й элемент k-й матрицы коэффициентов двумерного дискретно-косинусного преобразования размером М×М элементов, причем выбирают N<M, и формируют К матриц нормированных значений размером N×N элементов путем умножения каждого коэффициента Z_k(i,j) матрицы коэффициентов двумерного дискретно-косинусного преобразования размером NхN элементов на соответствующий ему элемент нормировочной матрицы размером N×N элементов. Затем генерируют случайную прямоугольную матрицу размером N×m единичных и нулевых элементов, из ее элементов формируют случайную прямоугольную матрицу размером m×N путем транспонирования случайной прямоугольной матрицы размером N×m элементов и выполняют цикл. При выполнении цикла каждую из случайных ключевых матриц размерами N×m и m×N суммируют по модулю 2 соответственно со случайными прямоугольными матрицами размерами N×m и m×N элементов. Полученные в результате такого суммирования К результирующих прямоугольных матриц размером N×m и К результирующих прямоугольных матриц размером m×N единичных и нулевых элементов преобразуют путем деления элементов каждой строки каждой результирующей прямоугольной матрицы размером N×m на сумму единиц соответствующей строки и деления элементов каждого столбца каждой результирующей прямоугольной матрицы размером m×N на сумму единиц соответствующего столбца. Далее в цикле вычисляют К результирующих матриц размером N×N элементов путем последовательного умножения соответствующих преобразованной результирующей прямоугольной матрицы размером N×m на случайную квадратную матрицу размером m×m и на преобразованную результирующую прямоугольную матрицу размером m×N элементов, первоначально вычисляют среднеквадратическую ошибку между элементами каждой результирующей матрицы размером N×N и соответствующими элементами соответствующей матрицы нормированных значений размером N×N элементов, вычисляют их итоговую сумму и выполняют подцикл. При выполнении подцикла последовательно инвертируют каждый элемент случайной прямоугольной матрицы размером N×m, соответствующий ему по правилу транспонирования элемент случайной прямоугольной матрицы размером m×N и соответствующие этим элементам элементы результирующих прямоугольных матриц размерами N×m и m×N элементов, а после инверсии этих элементов преобразуют результирующие прямоугольные матрицы путем деления элементов каждой строки каждой результирующей прямоугольной матрицы с инвертированным элементом размером N×m элементов на сумму единиц соответствующей строки и деления элементов каждого столбца каждой результирующей прямоугольной матрицы с инвертированным элементом размером m×N элементов на сумму единиц соответствующего столбца. Далее в подцикле повторно вычисляют К результирующих матриц размером N×N элементов путем последовательного умножения соответствующей преобразованной результирующей прямоугольной матрицы с инвертированным элементом размером N×m на случайную квадратную матрицу размером m×m и на соответствующую преобразованную результирующую прямоугольную матрицу с инвертированным элементом размером m×N элементов, вычисляют среднеквадратическую ошибку между элементами каждой из К повторно вычисленных результирующих матриц размером N×N и соответствующими элементами соответствующей матрицы нормированных значений размером N×N элементов, вычисляют их итоговую сумму и сравнивают ее с предыдущей итоговой суммой. Далее по каналу связи передают, а на приемной стороне принимают из канала связи случайную прямоугольную матрицу размером N×m единичных и нулевых элементов и из ее элементов на приемной стороне формируют случайную прямоугольную матрицу размером m×N путем транспонирования случайной прямоугольной матрицы размером N×m элементов. Далее на приемной стороне каждую из случайных ключевых матриц размерами N×m и m×N единичных и нулевых элементов суммируют по модулю 2 соответственно со случайными прямоугольными матрицами размерами N×m и m×N элементов, а полученные в результате такого суммирования К результирующих прямоугольных матриц размером N×m и К результирующих прямоугольных матриц размером m×N единичных и нулевых элементов преобразуют путем деления элементов каждой строки каждой результирующей прямоугольной матрицы размером N×m элементов на сумму единиц соответствующей строки и деления элементов каждого столбца каждой результирующей прямоугольной матрицы размером m×N элементов на сумму единиц соответствующего столбца. Затем на приемной стороне вычисляют К результирующих матриц размером N×N элементов путем последовательного умножения соответствующей преобразованной результирующей прямоугольной матрицы размером N×m на случайную квадратную матрицу размером m×m и на соответствующую преобразованную результирующую прямоугольную матрицу размером m×N элементов, преобразуют результирующие матрицы размером N×N путем поэлементного деления их элементов на соответствующие элементы нормировочной матрицы размером N×N элементов, а полученные в результате такого деления К матриц восстановленных коэффициентов двумерного дискретно-косинусного преобразования размером N×N элементов дополняют нулями до размера М×М элементов. После этого восстанавливают каждую из К матриц неподвижных полутоновых изображений путем последовательного перемножения транспонированной матрицы дискретно-косинусного преобразования размером М×М элементов на соответствующую матрицу восстановленных коэффициентов двумерного дискретно-косинусного преобразования размером М×М элементов и на матрицу дискретно-косинусного преобразования размером М×М элементов и формируют К восстановленных неподвижных полутоновых изображений.

Для формирования К матриц квантованных отсчетов неподвижного полутонового изображения размерами М×М элементов каждому ее элементу S_k(q,w), где q=1,2,…, M, w=1,2,…, M, k=1,2,…, K, присваивают квантованное значение соответствующего пиксела К неподвижных полутоновых изображений размером М×М, которые и являются сообщениями.

Для представления К матриц квантованных отсчетов неподвижного полутонового изображения размером М×М элементов в виде К неподвижных полутоновых изображений каждому пикселу К неподвижных полутоновых изображений присваивают значение соответствующего элемента К матриц восстановленных квантованных отсчетов неподвижных полутоновых изображений размером М×М элементов.

Способ-прототип позволяет снизить требуемую скорость передачи информации по цифровым каналам связи при заданном качестве восстановления неподвижных полутоновых изображений на приемной стороне.

Недостатком способа-прототипа все же является относительно низкое качество восстановления сообщений при заданной скорости передаче информации по цифровому каналу связи. Это объясняется тем, что для снижения объема передаваемых данных и соответственно для снижения требуемой скорости передачи информации по каналу связи в способе-прототипе для кодирования одновременно К неподвижных полутоновых изображений только одной случайной прямоугольной матрицей размером N×m единичных и нулевых элементов, которую и передают по каналу связи, выполняют следующее.

Случайную прямоугольную матрицу размером N×m и сформированную из ее элементов путем транспонирования случайную прямоугольную матрицу размером m×N суммируют по модулю 2 соответственно со случайными ключевыми матрицами размерами N×m и m×N элементов, которые в общем случае различны для каждого из К изображений. Тем самым из одной передаваемой случайной прямоугольной матрицы размером N×m получают по К результирующих прямоугольных матриц размерами N×m и m×N элементов, которые непосредственно кодируют передаваемые изображения. При этом для кодирования и восстановления каждого K-го передаваемого изображения существует только по одной случайной ключевой матрице размерами N×m и m×N элементов. В результате введения перечисленных ограничений резко сокращается число возможных вариантов непосредственного цифрового представления каждого передаваемого изображения соответствующими результирующими матрицами и качество восстановленных изображений, которые и являются сообщениями, оказывается значительно хуже, чем без введения ограничений.

Технической задачей является повышение качества восстановления сообщений на приемной стороне при сохранении заданной скорости передачи информации по каналу связи.

Решение технической задачи достигается тем, что в известном способе сжатия и восстановления сообщений, в котором предварительно до начала сеанса связи на передающей и приемной сторонах идентично генерируют случайную квадратную матрицу размером m×m элементов, каждый элемент которой принадлежит диапазону от -500 до 500, и по К>1 случайных ключевых матриц размерами N×m и m×N единичных и нулевых элементов формируют нормировочную матрицу размером N×N элементов, элементы которой C(i,j) вычисляют по формуле С(i,j)=(i+j)/(2×М), где i=1,2,…, N, 7=1,2,…, N, далее при ведении сеанса связи на передающей стороне К матриц квантованных отсчетов неподвижного полутонового изображения размером М×М элементов представляют в виде К матриц нормированных значений размером N×N элементов, для чего формируют К матриц коэффициентов двумерного дискретно-косинусного преобразования размером М×М элементов путем последовательного перемножения матрицы дискретно-косинусного преобразования размером М×М элементов на каждую матрицу квантованных отсчетов неподвижного полутонового изображения размером М×М элементов и на транспонированную матрицу дискретно-косинусного преобразования размером М×М элементов, формируют К матриц коэффициентов двумерного дискретно-косинусного преобразования размером N×N элементов, по формуле Z_k(i,j)=H_k(i,j), где i=1,2,…, N, j=1,2,…, N, k=1,2,…, K, H_k(i,j) - ij-й элемент k-й матрицы коэффициентов двумерного дискретного косинусного преобразования размером М×М элементов, Z_k(i,j) - ij-й элемент k-й матрицы коэффициентов двумерного дискретно-косинусного преобразования размером N×N элементов, причем выбирают N<M, и формируют К матриц нормированных значений размером N×N элементов путем умножения каждого коэффициента Z_k(i,j) матрицы коэффициентов двумерного дискретно-косинусного преобразования размером N×N элементов на соответствующий ему элемент нормировочной матрицы размером N×N элементов, затем генерируют случайную прямоугольную матрицу размером N×m единичных и нулевых элементов, из ее элементов формируют случайную прямоугольную матрицу размером m×N путем транспонирования случайной прямоугольной матрицы размером N×m элементов и выполняют цикл, в котором каждую из случайных ключевых матриц размерами N×m и m×N суммируют по модулю 2 соответственно со случайными прямоугольными матрицами размерами N×m и m×N элементов, полученные в результате такого суммирования К результирующих прямоугольных матриц размером N×m и К результирующих прямоугольных матриц размером m×N единичных и нулевых элементов преобразуют путем деления элементов каждой строки каждой результирующей прямоугольной матрицы размером N×m на сумму единиц соответствующей строки и деления элементов каждого столбца каждой результирующей прямоугольной матрицы размером m×N на сумму единиц соответствующего столбца, вычисляют К результирующих матриц размером N×N элементов путем последовательного умножения соответствующих преобразованной результирующей прямоугольной матрицы размером N×m на случайную квадратную матрицу размером m×m и на преобразованную результирующую прямоугольную матрицу размером m×N элементов, первоначально вычисляют среднеквадратическую ошибку между элементами каждой результирующей матрицы размером N×N и соответствующими элементами соответствующей матрицы нормированных значений размером N×N элементов, вычисляют их итоговую сумму и выполняют подцикл, в котором последовательно инвертируют каждый элемент случайной прямоугольной матрицы размером N×m, соответствующий ему по правилу транспонирования элемент случайной прямоугольной матрицы размером m×N и соответствующие этим элементам элементы результирующих прямоугольных матриц размерами N×m и m×N элементов, а после инверсии этих элементов преобразуют результирующие прямоугольные матрицы путем деления элементов каждой строки каждой результирующей прямоугольной матрицы с инвертированным элементом размером N×m элементов на сумму единиц соответствующей строки и деления элементов каждого столбца каждой результирующей прямоугольной матрицы с инвертированным элементом размером m×N элементов на сумму единиц соответствующего столбца, повторно вычисляют К результирующих матриц размером N×N элементов путем последовательного умножения соответствующей преобразованной результирующей прямоугольной матрицы с инвертированным элементом размером N×m на случайную квадратную матрицу размером m×m и на соответствующую преобразованную результирующую прямоугольную матрицу с инвертированным элементом размером m×N элементов, вычисляют среднеквадратическую ошибку между элементами каждой из К повторно вычисленных результирующих матриц размером N×N и соответствующими элементами соответствующей матрицы нормированных значений размером N×N элементов, вычисляют их итоговую сумму и сравнивают ее с предыдущей итоговой суммой, далее по каналу связи передают, а на приемной стороне принимают из канала связи случайную прямоугольную матрицу размером N×m единичных и нулевых элементов и из ее элементов формируют случайную прямоугольную матрицу размером m×N путем транспонирования случайной прямоугольной матрицы размером N×m элементов, далее каждую из случайных ключевых матриц размерами N×m и m×N единичных и нулевых элементов суммируют по модулю 2 соответственно со случайными прямоугольными матрицами размерами N×m и m×N элементов, полученные в результате такого суммирования К результирующих прямоугольных матриц размером N×m и К результирующих прямоугольных матриц размером m×N единичных и нулевых элементов преобразуют путем деления элементов каждой строки каждой результирующей прямоугольной матрицы размером N×m элементов на сумму единиц соответствующей строки и деления элементов каждого столбца каждой результирующей прямоугольной матрицы размером m×N элементов на сумму единиц соответствующего столбца, вычисляют К результирующих матриц размером N×N элементов путем последовательного умножения соответствующей преобразованной результирующей прямоугольной матрицы размером N×m на случайную квадратную матрицу размером M×M и на соответствующую преобразованную результирующую прямоугольную матрицу размером m×N элементов, преобразуют результирующие матрицы размером N×N путем поэлементного деления их элементов на соответствующие элементы нормировочной матрицы размером N×N элементов, полученные в результате такого деления К матриц восстановленных коэффициентов двумерного дискретно-косинусного преобразования размером N×N элементов дополняют нулями до размера м×м элементов, после чего восстанавливают каждую из К матриц неподвижных полутоновых изображений путем последовательного перемножения транспонированной матрицы дискретно-косинусного преобразования размером М×М элементов на соответствующую матрицу восстановленных коэффициентов двумерного дискретно-косинусного преобразования размером М×М элементов и на матрицу дискретно-косинусного преобразования размером М×М элементов и формируют К восстановленных неподвижных полутоновых изображений, предварительно до начала сеанса связи на передающей и приемной сторонах дополнительно идентично генерируют по (G-1)×K, где G>1, случайных ключевых матриц размерами N×m и m×N и формируют матрицу разрешенных кодовых групп размером G×m₁, где m₁≤m, единичных и нулевых элементов. Далее при ведении сеанса связи на передающей стороне до начала выполнения цикла общую среднеквадратическую ошибку принимают равной бесконечно большому числу, затем цикл выполняют G раз. При этом при каждом g-м, где g=1,2,…, G, выполнении цикла после первоначальной генерации случайной прямоугольной матрицы размером N×m единичных и нулевых элементов первые m₁ элементов N-й строки этой матрицы назначают равными соответствующим элементам g-й строки матрицы разрешенных кодовых групп размером g×w] элементов и инверсии не подвергают, а суммирование по модулю 2 случайных прямоугольных матриц размерами N×m и m×N элементов выполняют с соответствующими k-му изображению g-ми случайными ключевыми матрицами размерами N×m и m×N элементов. Кроме того, при каждом G×m₁ выполнении цикла после сравнения итоговой суммы среднеквадратических ошибок между соответствующими элементами результирующих матриц и матриц нормированных значений размером N×N элементов, полученной в подцикле после инверсии элемента случайной прямоугольной матрицы размером N×m, с предыдущей итоговой суммой, если итоговая не меньше предыдущей итоговой, то итоговую сумму назначают равной предыдущей итоговой сумме, а инвертированные элементы случайных и результирующих прямоугольных матриц размерами N×m и m×N элементов инвертируют повторно. После же текущего выполнения подцикла последовательной инверсии всех элементов, для которых инверсия предусмотрена, итоговую сумму сравнивают с первоначально рассчитанной до начала текущего выполнения подцикла в текущем g-м выполнении цикла итоговой суммой среднеквадратических ошибок между соответствующими элементами результирующих матриц и матриц нормированных значений размером N×N элементов. Если при этом итоговая сумма меньше первоначально рассчитанной до текущего выполнения подцикла итоговой суммы, то первоначально рассчитанную итоговую сумму назначают равной итоговой сумме и выполняют подцикл повторно. В противном случае итоговую сумму сравнивают с общей среднеквадратической ошибкой. Если при этом итоговая сумма меньше общей среднеквадратической ошибки, то эту ошибку назначают равной итоговой сумме, и после этого сравнения, если текущее значение g<G, то значения элементов случайных ключевых матриц размерами N×m и m×N назначают равными значениям соответствующих элементов этих матриц, сгенерированных до начала выполнений цикла, и переходят к (g+1)-му выполнению цикла, если же g=G, то значения элементов случайных ключевых матриц размерами N×m и m×N назначают равными значениям соответствующих элементов этих матриц, полученных после такого g₀-го, где g₀=1,2,…, G, выполнения цикла, в конце которого общая среднеквадратическая ошибка приняла текущее значение. На приемной стороне после получения из канала связи случайной прямоугольной матрицы размером N×m единичных и нулевых элементов сначала исправляют ошибки в первых m₁ элементах N-й строки этой матрицы и определяют значение g₀, в дальнейшем суммирование по модулю 2 случайных прямоугольных матриц размерами N×m и m×N выполняют с соответствующими k-му изображению g₀-ми случайными ключевыми матрицами размерами N×m и m×N элементов.

Для формирования матрицы разрешенных кодовых групп размером G×m₁ единичных и нулевых элементов сначала каждую i-ю строку, где i=1,2,…, m₁ и m₁=G/2, этой матрицы формируют в виде i-й дискретной функции Уолша из упорядоченного множества m₁ дискретных функций Уолша длины m₁, где m₁=2^u и u=3,4,…, затем в каждой сформированной строке всем элементам, равным -1, присваивают значение 0 и затем каждую (i+m₁)-ю строку формируют путем инверсии всех элементов i-й строки. Для исправления же ошибок в первых m₁ элементах N-й строки, принятой из канала связи прямоугольной матрицы размером N×m единичных и нулевых элементов, и определения значения g₀ на приемной стороне первые m₁ элементов N-й строки, принятой из канала связи прямоугольной матрицы размером N×m, сравнивают с соответствующими элементами последовательно каждой строки матрицы разрешенных кодовых групп и определяют расстояние Хэмминга между этой строкой и первыми m₁ элементами N-й строки прямоугольной матрицы размером N×m. После этого значение g₀ назначают равным номеру, а первые m₁ элементов N-й строки прямоугольной матрицы размером N×m назначают равными соответствующим элементам той строки матрицы разрешенных кодовых групп, для которой расстояние Хэмминга минимально.

Благодаря новой совокупности существенных признаков за счет использования большего числа случайных ключевых матриц значительно увеличивается число возможных вариантов непосредственного цифрового представления кодируемых сообщений результирующими прямоугольными матрицами без увеличения объема передаваемых данных. Таким образом, предлагаемый способ для заданной скорости передачи информации по каналу связи позволяет осуществлять выбор оптимального варианта непосредственного цифрового представления передаваемых сообщений из большего числа возможных вариантов и тем самым существенно повысить качество восстановления сообщений.

Проведенный анализ показал, что аналоги, обладающие совокупностью признаков, тождественных всем признакам заявленного технического решения, отсутствуют. Следовательно, заявленный способ соответствует условию патентоспособности «новизна». Поиск известных решений в данной и смежных областях техники с целью выявления признаков, совпадающих с отличительными от прототипа признаками заявленного способа, показал, что они не следуют явным образом из уровня техники. Из уровня техники также не выявлена известность влияния предусматриваемых существенными признаками заявленного изобретения преобразований на достижение указанного технического результата. Следовательно, заявленный способ соответствует условию патентоспособности «изобретательский уровень».

Заявленный способ поясняется чертежами:

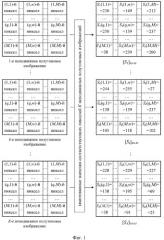
Фиг.1. Формирование К матриц квантованных отсчетов неподвижного полутонового изображения [S_k]_M×M.

Фиг.2. Формирование k-х матриц коэффициентов двумерного дискретно-косинусного преобразования [H_k]_M×M, [Z_k]_N×N и нормированных значений [A_k]_N×N.

Фиг.3. Последовательность преобразований К матриц нормированных значений [A_k]_N×N к цифровому виду на передающей стороне и обратных преобразований принятого из канала связи цифрового потока в К восстановленных матриц нормированных значений на приемной стороне.

Фиг.4. Формирование матрицы разрешенных кодовых групп и случайных прямоугольных матриц [Е₁]_N×m и [E₂]_m×N.

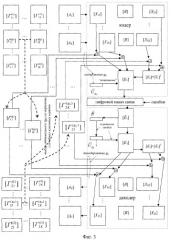
Фиг.5. Формирование результирующих прямоугольных матриц [X_1k]_N×m, [X_2k]_m×N и преобразованных результирующих прямоугольных матриц [X'_1k]_N×m, [X'_2k]_m×N.

Фиг.6. Пример инверсии элемента случайной прямоугольной матрицы [E₁]_N×m и соответствующих элементов случайной прямоугольной матрицы [E₂]_m×N и результирующих прямоугольных матриц [X_1k]_N×m, [X_2k]_m×N.

Фиг.7. Исправление ошибок в первых m₁ элементах N-й строки принятой из канала связи случайной прямоугольной матрицы [E₁]_N×m и определение на приемной стороне значения g₀.

Фиг.8. Восстановление k-x матриц коэффициентов двумерного дискретно-косинусного преобразования [Z_k]_N×N и [Н_k]_M×M и квантованных отсчетов неподвижного полутонового изображения [S_k]_M×M.

Фиг.9. Восстановление К неподвижных полутоновых изображений. Возможность реализации заявленного способа сжатия и восстановления сообщений, позволяющего повысить качество восстановления без увеличения объема передаваемых данных, объясняется следующим.

При необходимости передачи по каналу связи сообщения, объем которого превышает возможности канала связи или для передачи которого требуется недопустимо большой временной интервал, используют различные приемы сокращения объема передаваемых данных. Например (см. книгу: У.Претт. Цифровая обработка изображений. Часть 1. - М.: Мир, 1982, с.96-118), кодируемое сообщение представляют в виде произведения матрицы опорных векторов на матрицу коэффициентов разложения. Для этой цели используют один из известных приемов: дискретное косинусное преобразование, быстрое преобразование Фурье, преобразование Карунена-Лоэва, вейвлет-преобразование и другие. На приемной стороне из принятых данных сообщение восстанавливают. В способе-прототипе для еще большего снижения объема передаваемых данных, необходимых для восстановления одного сообщений, одинаковым объемом цифровых данных кодируется не одно, а одновременно несколько сообщений. Таким образом, при некотором ухудшении качества восстановленной информации не ниже требуемого обеспечивают снижение объема передаваемых данных до уровня, соответствующего скорости передачи в цифровом канале связи.

В то же время в случае повышения требований к качеству восстановления при сохранении скорости передачи по каналу связи обеспечить это повышение без увеличения объема передаваемых данных в способе-прототипе возможно только путем снижения числа К одновременно кодируемых сообщений. Однако это приведет к повышению объема передаваемой информации в расчете на одно сообщение, что в свою очередь может привести к увеличению времени передачи К сообщений до недопустимого уровня.

Для повышения качества восстановления без увеличения объема передаваемых данных в предлагаемом способе непосредственное кодирование и восстановление каждого k-го из К сообщений, в качестве которых далее рассматриваются неподвижные полутоновые изображения, осуществляют с помощью двух результирующих прямоугольных матриц [X_1k]_N×m, [X_2k]_m×N, полученных суммированием по модулю 2 (обозначается знаком ) случайных прямоугольных матриц [E₁]_N×m и и оптимальных g₀-x из G случайных ключевых матриц той же размерности и соответствующих k-му кодируемому изображению (фиг.3, 5,а). Таким образом, общее число разрешенных вариантов непосредственного цифрового представления каждого изображения, которыми располагает передатчик при выборе оптимального варианта, в G>1 раз больше, чем в способе-прототипе, где G=1, что обеспечивает большую точность кодирования, а соответственно и восстановления изображений.

Для того чтобы на приемной стороне правильно восстановить переданные изображения, приемник должен знать номер g₀ оптимальных из G случайных ключевых матриц. Поэтому на передающей стороне определяют и передают по каналу связи g₀-ю разрешенную кодовую группу (фиг.3, 4), которая является цифровым представлением номера g₀ оптимальных для кодирования К изображений случайных ключевых матриц. представляет собой g₀-ю строку матрицы разрешенных кодовых групп . Однако если эту группу передавать по каналу связи вместе с матрицей

[Е₁]_N×m, то это приведет к увеличению объема передаваемых данных и снижению коэффициента сжатия. Во избежание этого "встраивают" в матрицу [Е₁]_N×m на место первых m₁ элементов ее N-й строки (фиг.3, 4). Таким образом, этими элементами одновременно и кодируют номер оптимального варианта случайных ключевых матриц, и в совокупности с остальными элементами матрицы [E₁]_N×m кодируют К передаваемых изображений.

Предлагаемый способ предполагает выполнение следующих действий.

Предварительно до начала сеанса связи на передающей и приемной сторонах идентично генерируют случайную квадратную матрицу [B]_m×m и по G>1 случайных ключевых матриц и для каждого из К>1 передаваемых изображений, а так же формируют нормировочную матрицу [C]_N×N и матрицу разрешенных кодовых групп .

Генерация случайной квадратной матрицы [B]_m×m, каждый элемент которой принадлежит диапазону от -500 до 500, может быть выполнена с помощью датчика случайных чисел, например, на основе шумового диода. Для обеспечения идентичности матрицы [В]_m×m приемника аналогичной матрице передатчика ее элементы могут быть сгенерированы на передающей стороне и переданы по цифровому каналу связи на приемную сторону в составе синхропосылки.

Генерация случайных ключевых матриц и может быть выполнена на основе использования на передающей и приемной сторонах генераторов с регистром сдвига одинаковой структуры, которые описаны, например, в книге: У.Питерсон, Э.Уэлдон. Коды, исправляющие ошибки. - М.: Мир, 1976, с.206-212. При этом начальное заполнение генераторов может быть случайным образом выбрано на передающей стороне и передано на приемную сторону в составе синхропосылки.

Формирование нормировочной матрицы [С]_N×N (фиг.2, 8) выполняют путем вычисления значения каждого ее элемента С(i,j), где i=1,2,…, N, j=1,2,…, N по формуле C(i,j)=(i+j)/(2×M).

Формирование матрицы разрешенных кодовых групп , где m₁≤m и m₁=G/2, проиллюстрировано фиг.4. При этом на фиг.4,а показан случай, когда у строк матрицы длина m₁=8, а на фиг.4,б формирование представлено в общем виде. Каждая i-я строка, где i=1,2,…,m₁, матрицы является i-й дискретной функцией Уолша из упорядоченного множества дискретных функций Уолша длины m₁, в которой элементы, равные - 1, заменены на нулевые. Каждую (i+m₁)-ю строку матрицы получают инверсией элементов i-й строки этой же матрицы.

Используемые при формировании матриц разрешенных кодовых групп функции Уолша, их дискретизация и упорядочение описаны, например, в книге: Н.Ахмед, К.Р.Рао. Ортогональные преобразования при обработке цифровых сигналов. - М.: Радио и связь, 1980, с.86-89. Выбор одного из возможных упорядочений (например, по Уолшу, по Пэли, по Адамару) не является принципиальным, поскольку сами функции при любом упорядочении остаются неизменными.

При ведении сеанса связи К передаваемых неподвижных полутоновых изображений, которые далее рассматриваются в качестве передаваемых сообщений, размерами М×М пикселей каждое, как и в способе-прототипе представляют в виде соответствующих матриц нормированных значений [A_k]_N×N (фиг.1, 2). Для этого сначала формируют К матриц квантованных отсчетов неподвижного полутонового изображения [S_k]_M×M путем присвоения каждому элементу S_k(q,w), где q=1,2,…, M, w=1,2,…, M, k=1,2,…, K, квантованное значение соответствующего пиксела соответствующего k-го изображения. На фиг.1 приведен вариант значений S_k(q,w). Далее (фиг.2) с помощью двумерного дискретно-косинусного преобразования (далее ДКП) матриц [S_k]_M×M получают матрицы коэффициентов двумерного ДКП [Н_k]_M×M. ДКП, используемое с целью уменьшения объема данных, передаваемых по каналу связи, описано, например, в кн.: Н.Ахмед, К.Р.Рао. Ортогональные преобразования при обработке цифровых сигналов. - М.: Связь, 1980, с.156-159. Поскольку наиболее информативными для восстановления передаваемых изображений являются коэффициенты ДКП с максимальной энергией, располагающиеся в левом верхнем квадранте матриц [H_k]_M×M, то их выделяют, формируя матрицу коэффициентов двумерного ДКП [Z_k]_N×N, где N<M. После этого формируют матрицы нормированных значений [A_k]_N×N путем вычисления значения каждого элемента Ak(i,j), где i=1,2,…, N, j=1,2,…, N, по формуле A_k(i,j)=Z_k(i,j)·C(i,j). Необходимость такого нормирования связана с тем, что при отсутствии нормировки коэффициенты двумерного ДКП имеют очень широкий диапазон значений и существенно зависят от i и j.

Далее матрицы [A_k]_N×N, как и в способе-прототипе, одновременно кодируют с помощью передаваемой по каналу связи случайной прямоугольной матрицы [E₁]_N×m (фиг.3). Отличие процедуры кодирования в предлагаемом способе от процедуры в способе-прототипе в том, что в процессе поиска оптимального варианта матрицы

[E₁]_N×m (а соответственно оптимальных [Е₂]_m×N и [X_1k]_N×m, [X_2k]_m×N) одновременно осуществляют поиск оптимальных для кодирования случайных ключевых матриц и (a соответственно оптимального значения g=g₀). Кроме того, информацию о значении g₀ "встраивают" в передаваемую матрицу [Е₁]_N×m, как описано выше и проиллюстрировано фиг.4. Решаемая в к