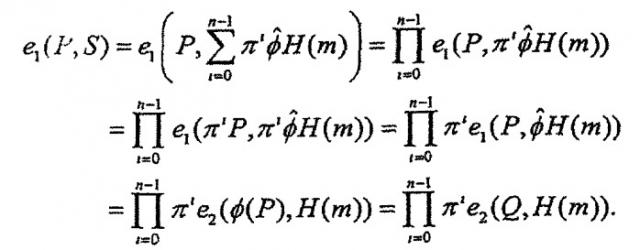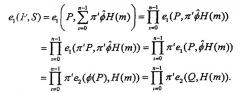Использование изогений для разработки криптосистем

Использование изогений для разработки криптосистем

Иллюстрации

Показать все

Реферат

РОДСТВЕННЫЕ ПАТЕНТНЫЕ ЗАЯВКИ

Данная заявка испрашивает приоритет предварительной патентной заявки США № 60/517,142 от 3 ноября 2003 г. на "Использование изогений для разработки криптосистем", раскрытие которой включено в данный документ посредством ссылки.

ОБЛАСТЬ ТЕХНИКИ

Данное изобретение относится к криптологии, в частности к использованию изогений для разработки криптосистем.

ПРЕДШЕСТВУЮЩИЙ УРОВЕНЬ ТЕХНИКИ

Поскольку цифровая связь становится все более распространенной, потребность в обеспечении защищенности каналов связи становится все более и более важной. Например, современные технологии позволяют пользователю дистанционно обращаться к счетам в банке, медицинским данным и другой частной и конфиденциальной информации.

Криптология широко используется для обеспечения защищенной цифровой связи. Криптология в принципе относится к зашифровыванию (или шифрованию) и расшифровыванию (дешифрованию) сообщений. Шифрование и дешифрование используют некоторую секретную информацию (такую как ключ). В различных методах шифрования единственный ключ или множество ключей могут быть использованы для шифрования и дешифрования.

Одной широко используемой криптосистемой с множественным ключом является система шифрования с открытым ключом. В криптосистеме с открытым ключом отправитель, желающий послать зашифрованное сообщение получателю, получает аутентифицированный (заверенный) открытый ключ для получателя, который генерируется с использованием секретного ключа. Как следует из названия, открытый ключ может быть доступен из общедоступных источников. Кроме того, чтобы избежать попыток взлома криптосистемы с использованием злоумышленником открытого ключа другого человека, часто проводится проверка подлинности открытого ключа. Проверка подлинности открытого ключа может быть реализована при помощи обмена ключами по защищенному каналу, использования защищенного открытого файла, использования защищенного сетевого сервера или использования несетевого сервера и сертификатов.

После получения аутентифицированного (т.е. подлинного) открытого ключа отправитель шифрует исходное сообщение с использованием открытого ключа и генерирует шифротекст. Санкционированный получатель затем использует секретный ключ, чтобы дешифровать шифротекст и извлечь исходное сообщение. Предполагается, что задача расшифровки шифротекста, без доступа к секретному ключу, является нерешаемой. Соответственно, только сторона, имеющая доступ к секретному ключу, может успешно расшифровать шифротекст.

Одним существенным преимуществом систем с открытым ключом над симметричными криптосистемами (например, системами поточного шифрования или блочного шифрования) является то, что при двустороннем обмене информацией только секретный ключ должен храниться в секрете (тогда как в симметричных криптосистемах ключ хранится в секрете обеими сторонами).

Существующие в настоящее время криптосистемы с открытым ключом используют эллиптические кривые определенного рода, построенные на конечных полях. Пара опубликованных значений, выведенных на основании уравнения эллиптической кривой, используется в качестве открытого ключа (включая точки на кривой и соответствующие им открытые ключи, сгенерированные при помощи простого (то есть целочисленного умножения на кривой). Верификация производится с использованием билинейных пар для кривой.

В общем случае считается, что эллиптические кривые обеспечивают криптосистемы с относительно более низкими требованиями к процессу передачи информации по сравнению с традиционными криптосистемами типа РША (шифр Ривеста-Шамира-Адлемана с открытым ключом), поддерживая такой же уровень безопасности.

Проблема современных криптосистем с открытым ключом заключается в том, что не может быть доказана защищенность ни одной из них. В результате защищенность данной криптосистемы с открытым ключом предполагается на основании сложности некоего набора теоретико-числовых проблем.

Соответственно, требуются криптосистемы с открытым ключом, обеспечивающие дополнительную защищенность.

КРАТКОЕ ОПИСАНИЕ

Заявлены способы, позволяющие создать криптосистему с открытым ключом. Более подробно, изогении абелевых множеств (например, эллиптические кривые в одномерном случае) используются для создания криптосистемы с открытым ключом. Например, изогении допускают использование множества кривых вместо единственной кривой для обеспечения большей защищенности. Способы могут быть использованы для цифровой подписи и/или для способов идентификационного шифрования (IBE). Кроме того, изогении могут быть использованы для других приложений, например "слепой" подписи, иерархических систем, и тому подобных. Кроме того, раскрыты решения для формирования изогений.

В одной из описанных реализаций способ включает в себя опубликование открытого ключа, соответствующего изогении. Далее способ включает дешифрование зашифрованного сообщения с использованием ключа дешифрования, соответствующего изогении (например, ее дуальной изогении).

КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ

Детальное описание приводится со ссылками на прилагаемые чертежи. На чертежах самая левая цифра(цифры) ссылочной позиции указывает на чертеж, на котором данная ссылочная позиция встречается впервые. Использование одинаковых ссылочных позиций на разных чертежах указывает на аналогичные или идентичные объекты.

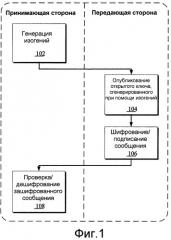
Фиг.1 иллюстрирует примерный способ использования изогений в криптосистеме.

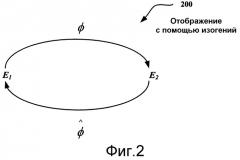
Фиг.2 иллюстрирует примерное отображение изогений между двумя кривыми.

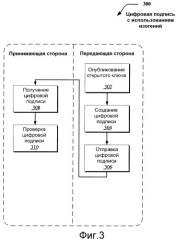
Фиг.3 иллюстрирует примерный способ подписи сообщения с использованием изогений.

Фиг.4 иллюстрирует примерное отображение изогений между множеством кривых.

Фиг.5 иллюстрирует примерный способ идентификационного шифрования (IBE) с использованием изогений.

Фиг.6 иллюстрирует вычислительную среду 600 общего назначения, которая может быть использована для реализации описанных здесь методик.

ПОДРОБНОЕ ОПИСАНИЕ ИЗОБРЕТЕНИЯ

Дальнейшее обсуждение подразумевает, что читатель знаком с методами криптографии. Для общего введения в криптографию читатель отсылается к кн.: A Menezes, P. van Oorschot, and S. Vanstone, "Handbook of Applied Cryptography", пятое изд. (август 2001), выпущенной издательством CRC Press.

Приведенное ниже раскрытие описывает методы улучшения систем с открытым ключом, основанные на множественных эллиптических кривых (или абелевых множествах, в общем случае). Раскрыты различные методы генерирования изогений (или отображений) между кривыми. Сгенерированные изогении допускают использование множества кривых вместо единственной кривой, для того чтобы обеспечить открытость шифрования. Кроме того, эти методы могут быть применены к относительно коротким цифровым подписям (например, введенным пользователем или посланным по узкополосным каналам связи) и/или к методам идентификационного шифрования (например, допускающим запоминающиеся открытые ключи). Так же короткие подписи могут обеспечить дополнительную эффективность за счет комплексной верификации.

Обзор криптосистем с использованием изогений

Фиг.1 иллюстрирует примерный способ 100 использования изогений в криптосистемах. На стадии 102 генерируются изогении (эллиптических кривых, или абелевых множеств, в более общем случае). Изогении могут быть сгенерированы принимающей стороной или другой стороной (например, доверенной стороной, как описано ниже со ссылкой на Фиг.5). На стадии 102 также могут быть сгенерированы соответствующие дуальные изогении для каждой сгенерированной изогении (как описано ниже). Различные способы генерации изогений рассмотрены подробно в соответствующем разделе. Кроме того, как детально описано ниже со ссылкой на Фиг.3 и 5, сгенерированные изогении используются для получения открытых ключей, и эти открытые ключи опубликовываются (104). Открытые ключи могут быть опубликованы передающей стороной или доверительным центром (см., например, описание Фиг.3 и 5).

Затем передающая сторона шифрует (или подписывает) сообщения при помощи ключа шифрования (106). Зашифрованные сообщения на стадии 106 могут быть верифицированы/дешифрованы принимающей стороной при помощи ключа дешифровки, чтобы определить подлинность шифрования или подписи (108). В одной реализации, для проверки зашифрованных сообщений, используется образование пар по Вейлу (как описано в соответствующем разделе), которое, однако, не является единственным примером образования пар, использующегося для верификации или дешифровки. Например, может быть использован другой метод билинейного и/или невырожденного образования пар, например, по Тейту или квадратичное образование пар.

Обзор изогений

Фиг.2 иллюстрирует примерное отображение изогений 200 между двумя кривыми (например, эллиптическими). Как показано, кривая E₁ может отображаться на кривую E₂ посредством изогении ϕ (где ). Фиг.1 также показывает дуальную изогению (где ).

В различных реализациях использования изогений в криптосистемах стараются обеспечить следующие свойства: для данной кривой E₁ генерирование пары (ϕ,E₂) достаточно эффективно, где - изогения, но для заданной пары (E₁, E₂) изогенных кривых предполагается, что достаточно трудно построить ненулевую изогению , которая будет много меньше заданной изогении. Таким образом, если разделить глобальный взлом (определяемый как вычисление, позволяющее взломать любое последующее сообщение в полиномиальное время) и поэтапный взлом, то наилучшая из известных в настоящее время атак на криптосистемы на основе изогений требует или существенно большего времени, чем дискретное логарифмирование, в случае глобального взлома и или одного дискретного логарифмирования на одно сообщение в случае простого поэтапного взлома.

Для примера рассмотрим систему лексем, в которой каждому клиенту выдается определенное снабженное подписью сообщение, предоставляющее доступ к определенному сервису (которое может иметь невысокое значение), клиент может зачитать лексему по телефону уполномоченному лицу, и таким образом цифровые подписи могут быть относительно короткими. В таком случае разумно использовать достаточно большие параметры, с тем чтобы сделать взлом отдельного сообщения более затратным чем стоимость предоставляемого сервиса, сохранив при этом, неприемлемо высокими затраты на глобальный взлом.

Подробное описание изогений

Поле k может быть упорядоченно при помощи характеристики p, содержащей q элементов и имеющее алгебраическое замыкание . Пусть E/k есть эллиптическая кривая, определенная по полю k, и E/k есть группа, определенная по k, и k(E) обозначает поле функции эллиптической кривой. Также пусть [n]_E или [n] обозначает отображение на E, а E[n] обозначает ядро этого отображения.

Изогения есть непостоянный морфизм, преобразующий нулевой элемент E₁ в соответствующий элемент E₂. Если такая изогения существует, можно сказать, что E₁ и E₂ изогенны. Изогения определена по k, если ϕ определяется уравнениями с коэффициентами, принадлежащими k. Также оказывается, что для любой изогении выполняется гомоморфизм групп, то есть для всех , где сложение в левой части есть групповой закон на E_1, а сложение в правой части - на E₂. Следовательно, ядро ϕ является подгруппой E₁.

Пусть обозначает множество изогений от E₁ и E₂, определенных по k. обозначим, как . Для любой изогении существует дуальная изогения такая, что:

и ,

где есть степень изогении. Дуальная изогения удовлетворяет стандартным свойствам

В одной реализации степень ϕ как конечное отображение может быть в дальнейшем определена как степень расширения k(E₁) над прообразом (по ϕ) поля k(E₂), где ϕ определена по k. Удобно рассматривать ее в терминах размера ее ядра (предполагая, что расширение поля функции сепарабельно) или при помощи приведенного выше уравнения. Поэтому говорят, что изогения имеет гладкость B-го порядка, если ее степень имеет гладкость B-го порядка (другими словами, простой дивизор для меньше либо равен B). Множество эндоморфизмов эллиптической кривой обозначим ; это множество имеет циклическую структуру, задаваемую определением:

, .

В общем случае группа является свободным левым и правым модулем кручения. Когда , алгебраическая структура более богата: является циклом (а не просто модулем) без нулевых дивизоров и имеет характеристический ноль.

В одном варианте реализации это может рассматриваться как структура: пусть E есть эллиптическая кривая, определенная по некоторому полю k. Тогда изоморфно или к рангу Z квадратичного мнимого поля, или к максимальному рангу в алгебре кватернионов. Для любых двух эллиптических кривых E₁, E₂ группа является свободным Z-модулем с рангом, не превышающим 4. Если больше чем Z, можно сказать, что E обладает комплексным умножением. Элемент в , соответствующий фробениусовому эндоморфизму , обозначается π и удовлетворяет характеристическому уравнению . Кондуктор эллиптической кривой с равен .

Образование пар по Вейлу

Образование пар по Вейлу представляет собой билинейное, невырожденное отображение со значениями в группе n-ных корней из единицы в k. В одном варианте реализации образование пар по Вейлу используется для выполнения стадии 108 верификации/дешифрования на Фиг.1. Тем не менее, образование пар по Вейлу не является единственным примером образования пар, которое может быть использовано для верификации или шифрования. Например, может быть использован другой метод билинейного и/или невырожденного образования пар, такой как образование пар по Тейту или квадратичное образование пар. Образование пар по Вейлу удовлетворяет следующему уравнению:

, где , ,

здесь есть вычисление для образования пар на E₁, а - на E₂. Заметим, что обе кривые имеют точки кручения n-го порядка, каждая из которых накладывает ограничение на соответствующие порядки групп. Это не создает проблемы, так как по теореме Тейта k(E₁) и k(E₂) изогенны по k тогда и только тогда, когда две группы точек имеют одинаковый порядок.

При образовании пар по Вейлу оценивается идентичность для всех линейно зависимых входных пар. Следовательно, полезен механизм, позволяющий удостовериться в том, что входные пары не являются скалярными произведениями друг друга. Один из подходов заключается в использовании кривой E₂, определенной по конечному полю k, достаточно большому, для того чтобы полная группа точек кручения n-го порядка определялась по k. В этом случае вероятность того, что два случайно выбранных элемента группы линейно зависимы, пренебрежимо мала, порядка 1/n, и таким образом результат образования пар по Вейлу может быть нетривиальным с высокой вероятностью. Приведенное выше уравнение гарантирует, что распределение парных значений на E₁ будет соответствовать распределению на E₂.

В качестве альтернативы может быть использована модифицированная функция пересчета пар , где λ - любой нескалярный эндоморфизм, такой что P и λ(P) линейно независимы и . Такое отображение λ называется дисторсией или изгибом E.

Формирование изогений

В различных вариантах реализации ряд способов может быть использован для построения изогений высокой степени (например, эллиптических кривых или абелевых множеств в более общем случае) и дуальных к ним, как описано со ссылкой на стадию 102, представленную на Фиг.1. Короткая цифровая подпись или идентификационные (IBE) криптосистемы, описываемые здесь, могут придерживаться соглашения о том, что пары значений опубликовываются в качестве открытого ключа, а оценка дуальной изогении является секретным ключом.

В одном из вариантов реализации формирование может быть кратко описано следующим образом: для любого заданного E существует алгоритм построения изогений , степени n которых распределены случайным образом и являются простым числом с вероятностью ; для любой заданной кривой E₁ существует алгоритм формирования случайных изогений, имеющих гладкость B-го порядка, из E₁ к случайным целям за время ; и для заданных E₁, E₂ и двух линейно независимых изогений в , имеющих взаимно простые степени, существует алгоритм формирования изогений с простыми степенями (как описано ниже для независимых изогений).

Комплексное умножение изогений

Пусть, как и ранее, , и предположим, что E₁ обладает комплексным умножением (CM) на мнимый квадратичный порядок O_D с дискриминантом . Вероятностный алгоритм для построений такой кривой E₁ вместе с эндоморфизмом ϕ над E₁ большой простой степени, в полиномиальное по время, может быть описан следующим образом.

1. Вычислить гильбертов полином с дискриминантом D. Пусть K обозначает поле разложения по Q.

2. Выбрать любой корень x полинома и построить эллиптическую кривую E по C, такую, что ее инвариант j равен x. Отметим, что E определена для поля чисел K.

3. Кривая E обладает комплексным умножением на по построению. Используя линейную алгебру q-расширений, найти в явном виде рациональную функцию с коэффициентами из K, соответствующую изогении

4. Выбрать случайные целые a и b до тех пор, пока не станет простым числом. В этом случае изогения будет эндоморфизмом E с простой степенью.

5. Выбрать любой простой идеал P поля K и редуцировать коэффициенты E и I по модулю P. Пусть E₁ обозначает редукцию E, а ϕ - редукцию

Стадии 1-3 данного алгоритма детерминированы и требуют полиномиального по времени. Что касается стадии 4, из теоремы простых чисел в числовом поле следует, что вероятность нахождения , являющегося простым числом, равна , таким образом, для целых чисел a и b мощности n можно ожидать завершения стадии 4 после попыток.

Найденный эндоморфизм ϕ есть эндоморфизм кривой E₁ с простой степенью. Изогения ϕ и дуальная к ней могут быть вычислены, если известны числа a и b, с использованием рациональной функции , комплексного умножения и сложения. Такая изогения ϕ может быть названа CM-изогенией.

Модулярные изогении

Для любого простого числа модулярная кривая задает в неявной форме изоморфизм класса изогений степени . А именно существует полиномиальное уравнение для такое, что E₁ и E₂ -изогенны тогда и только тогда, когда .

Используя полином , можно вычислить -изогенную кривую E₂ для любой E₁ вместе с явным полиномиальным уравнением для степени изогении . Так как модулярный полином симметричен по X и Y, вычисление с обращенными инвариантами j может быть использовано для нахождения дуальной изогении.

На практике лучше не использовать полиномы для реальных вычислений, потому что коэффициенты этих полиномов очень велики. Вместо них могут быть использованы другие эквивалентные полиномиальные модели для с меньшими коэффициентами. Безотносительно к точности, использованной для вычисления модели, изогении, выведенные таким способом, могут называться модулярными изогениями.

Как правило, известные в настоящий момент алгоритмы для вычисления модулярных изогений выполнимы для малых значений . Само по себе использование модулярных изогений малых степеней не сильно увеличивает надежность шифра, так как нарушитель, знающий кривые E₁ и E₂, может проверить, являются ли они -изогенными для каждого , и восстановить -изогению в случае положительного результата проверки. Тем не менее, можно скомпоновать множество модулярных изогений (например, для разных ) в одну изогению ϕ с большой степенью гладкости и использовать ϕ в качестве изогений без раскрытия промежуточных кривых. Нарушитель, способный вычислять в произвольных точках, все еще сможет вывести простые числа при помощи расчета всех точек кручения -го порядка на E₁ и проверки, сводятся ли к нулю какие-нибудь из них при применении ϕ. Тем не менее, если предположить, что проблема вычисления дуальных изогений сложна, нарушитель не сможет вычислить значения ϕ в точках по своему выбору. В процессе реализации, для улучшения, можно скомпоновать результирующую изогению или со скалярными изогениями, или с CM-изогениями, для того чтобы ввести большие негладкие множители степени.

Линейно независимые изогении

В одной из реализаций линейно независимые изогении ϕ и ψ задаются на E₁ и E₂ с взаимно простыми степенями. В результате линейная комбинация имеет степень, задаваемую квадратичной формой с двумя переменными a и b. Заметим, что коэффициенты квадратичной формы - целые числа, так как внешние коэффициенты есть степени ϕ и ψ, а средний коэффициент равен . Так как квадратичная форма является примитивной, она принимает значения, являющиеся простыми числами бесконечно часто, когда a и b изменяются по всем парам . Таким образом, может быть получено множество изогений с большими негладкими (и даже простыми) степенями. Также можно оценить вероятность того, что результирующая степень будет негладкой.

Схемы короткой цифровой подписи с использованием изогений

В возможной реализации описываемые методы могут быть применены к схемам с относительно короткими цифровыми подписями (например, введенными пользователем или посланными по узкополосным каналам связи). Ниже описаны две схемы цифровой подписи, частично базирующиеся на математических свойствах изогений и образовании пар эллиптических кривых.

Цифровая подпись на инвариантах Галуа

Обозначим расширение конечных полей степени n. Возьмем эллиптическую кривую E₁, определенную по F_q, вместе с изогенией , определенной по F_q”, где E₂ есть эллиптическая кривая, определенная по F_q'. В одной реализации кривая E₂ определена для L, а не для подполя от L, тем не менее, возможно использование E₂, определенной только для подполя. Однако изогения ϕ может быть неопределенна по любому надлежащему подполю F_q'. Более того, изогения ϕ может генерироваться в соответствии с методами, описанными выше.

Фиг.3 иллюстрирует примерный метод 300 для подписи сообщения с использованием изогений. Метод 300 включает следующие стадии:

Открытый ключ. Взять случайное и опубликовать (302), где . Заметим, что P определено по F_q, но Q не определено по F_q, так как ϕ не определено по F_q.

Секретный ключ. Дуальная изогения к ϕ.

Цифровая подпись. Пусть H есть (открытый) случайный оракул из пространства сообщения на множество точек кручения k-го порядка на E₂. Для данного сообщения m вычислить (стадия 304, обеспечивающая подпись при помощи секретного ключа, сгенерированного, как описано выше), где π есть фробениусово отображение мощности q, а сумма обозначает сумму эллиптической кривой на E₁. Для удобства обозначим оператор как Tr (от английского слова "trace"). Вывести в качестве подписи. Затем подпись посылается и получается принимающей стороной (306 и 308, соответственно). Заметим, что группа Галуа для F_q'/F_q есть , так что S есть инвариант Галуа, и таким образом определена по F_q.

Проверка. Пусть e₁ и e₂ обозначают пары по Вейлу на и , соответственно. Для данного открытого ключа и пары сообщение-подпись проверить, выполняется ли соотношение (стадия 310, проверяющая полученную сигнатуру с использованием открытого ключа, сгенерированного как описано выше). Соответственно подлинная подпись удовлетворяет данному уравнению, как следует ниже:

Также отображение следа может быть применено к базовому полю, для того чтобы сократить количество точек на эллиптической кривой (или любом абелевом множестве в более общем случае). Другими словами, вывод отображения следа на эллиптические кривые (или абелевых множеств более высокой размерности) может быть использован как способ для укорачивания представления точки по полю расширения с использованием данных по меньшему полю.

Подписание с использованием множественных эллиптических кривых

Другой способ увеличения устойчивости схем, использующих короткую подпись, заключается в применении множественных открытых ключей и сложении результирующих цифровых подписей. Эта модификация может быть использована отдельно или в комбинации с расширением на основе инварианта Галуа, описанного выше.

Со ссылкой на Фиг.4 предположим, что существует семейство изогений и семейство хэш-функций H_i случайного оракула, каждое из которых отображает сообщение m в точку на эллиптической кривой E_i. Аналогично стадиям, обсужденным со ссылкой на Фиг.3:

Открытый ключ. Взять случайное и опубликовать (см., например, 302), где .

Секретный ключ. Семейство изогений ϕ_i.

Цифровая подпись. Для каждого сообщения m цифровой подписью для m(S) является (см., например, 304). Затем подписанное сообщение отправляется принимающей стороне (см., например, 306).

Проверка. Для данной пары (сообщение, подпись) проверить, выполняется ли соотношение (см., например, стадию 306, описанную со ссылкой на Фиг.3). Для подлинной подписи это уравнение имеет место, так как:

.

Предполагается, что такая система по меньшей мере так же надежна, как и система, использующая единственную изогению, так как тот, кто может взломать версию системы, использующую множество изогений, может свести версию, использующую единственную изогению, к множественной, добавлением изогений , по своему усмотрению. Более того, для подобных систем успешная атака на версию системы с множеством изогений требует одновременного взлома всех единичных изогений от ϕ₁ до ϕ_n.

Схема идентификационного шифрования (IBE) с изогениями

Фиг.5 иллюстрирует примерный способ 500 для идентификационного шифрования (IBE) с использованием изогений. Считается, что использование необратимых изогений между эллиптическими кривыми делает схему идентификационного шифрования (IBE) потенциально более надежной, по сравнению с использованием программно реализуемой системы Диффи-Хеллмана (CHD). Схема IBE может быть определена следующим способом.

Отображение в точку: Определим оператор для некоторой кривой E. Более определенно, можно вычислить и использовать полученное значение для определения точки. Можно предположить, что H ведет себя подобно случайному оракулу. В качестве альтернативы, можно поддерживать таблицу точек и хэшировать в случайную последовательность весов, а затем вычислить взвешенную сумму. Также можно предположить, что существуют доверительный центр и конечное множество пользователей с некоторым , при помощи которого можно вычислить соответствующий открытый ключ. Каждый пользователь получает свой секретный ключ после соответствующей идентификации доверительным центром.

Открытый ключ для доверительного центра: , . Соответственно доверительный центр (или другая организация, например, принимающая сторона) обеспечивает и публикует открытые ключи (502). Если используется изгиб λ, можно предположить, что есть скрученный образ некоторой точки α.

Секретный ключ для доверительного центра: Эффективно вычисляемая .

Например, передача зашифрованных данных от Боба к Алисе может быть реализована следующим образом:

Открытый ключ для Алисы: предоставляется, например, посредством функции отображение-в-точку (502) доверительным центром (или другой организацией, например принимающей стороной).

Секретный ключ для Алисы: . Заметим, что атака, направленная на быстрое получение секретного ключа каждого клиента, будет требовать такого же времени, как для глобального взлома системы цифровой подписи (как описано выше). В результате эти системы можно также назвать двухуровневыми системами.

Шифрование, осуществляемое Бобом: Вычислить (стадия 504, которая зашифровывает сообщение при помощи сгенерированного открытого ключа). Пусть сообщение обозначается как m. Выбрать случайное целое r. Послать Алисе пару (506):

Дешифрование, осуществляемое Алисой: Пусть зашифрованный текст будет обозначен как . Отправленное зашифрованное сообщение дешифруется (508) с использованием секретного ключа (510), предоставленного доверительным центром (или другой организацией, например принимающей стороной) после соответствующей идентификации. В результате расшифрованный текст есть:

Эта схема работает, потому что величина, хэшированная на стадии шифрования, есть:

и равна величине, хэшированной на стадии дешифрования. Изогения может быть представлена, как описано ниже (например, с использованием вероятностного подхода, применяющего таблицу записей).

Задание изогений

Если изогения гладкая, то она может быть представлена как композиция изогений малой степени, задаваемых простой программой, представляющей собой вычисление полиномов. Для кривых, определенных по расширениям, представляющим инте