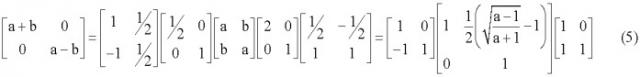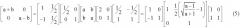Оператор обратимого перекрытия для эффективного сжатия данных без потерь

Оператор обратимого перекрытия для эффективного сжатия данных без потерь

Иллюстрации

Показать все

Реферат

Область техники, к которой относится изобретение

Изобретение относится к сжатию цифрового мультимедиа (к примеру, видео и изображений) с помощью преобразования с перекрытием.

Предшествующий уровень техники

Преобразования с перекрытием

Преобразование с перекрытием - это мощная методика обработки сигналов, которая используется при сжатии данных. См., к примеру, H. S. Malvar, "Signal Processing with Lapped Transforms", Boston, MA: Artech House, 1992 г. Тем не менее, до настоящего времени эффективные преобразования с перекрытием с линейной фазой не были сформулированы и никогда не применялись для сжатия данных без потерь (обратимого).

Как описано более подробно ниже, известно, что преобразование с перекрытием может быть сформулировано как предварительный фильтр, за которым следует преобразование данных (и его инверсия как обратное преобразование данных, за которым следует постфильтр). См., к примеру, H. S. Malvar, "A pre- and post-filtering technique for the reduction of blocking effects", на Proc. Picture Coding Symposium, Стокгольм, Швеция, июнь 1987 г.; и T.D. Tran, J. Liang и C. Tu, "Lapped Transform via Time-Domain Pre- and Post-Filtering", IEEE Trans. on Signal Processing, том 51, номер 6, июнь 2003 г. Преобразование данных без потерь может быть использовано в данной формулировке, чтобы достичь хорошего показателя обратимости. До настоящего времени считалось, что только определенное ограниченное множество предварительных фильтров и постфильтров может быть выбрано для обратимости. Этот ограниченный набор очень ограничен в своей производительности сжатия (скорость по сравнению с искажением, или R-D). В новой статье (W. Dai и T. Tran, "Regularity-constrained pre- and post-filtering for block DCT-based systems", IEEE Trans. on Signal Processing, том 51, стр.2568-2581, октябрь 2003 г.), была представлена структура, в которой большинство элементов являются обратимыми и которая имеет хорошие свойства сжатия.

В сжатии звука было внедрено несколько структур для обратимых преобразований с перекрытием. См., к примеру, R. Geiger, J. Herre, J. Koller и K. Brandenburg, "IntMDCT - A link between perceptual and lossless audio coding", на Proc. IEEE Int. Conf. on Acoustics, Speech, and Signal Processing, Орландо, штат Флорида, май 2002 г.; и J. Li, "Reversible FFT and MDCT viva matrix lifting", на Proc. IEEE Int. Conf. on Acoustics, Speech, and Signal Processing, Монреаль, Канада, май 2004 г. Тем не менее, эти структуры применимы только к модулированному преобразованию с перекрытием (MLT), также известному как модифицированное дискретное косинусное преобразование (MDCT), базисные функции которого являются ортогональными и не являются симметричными (т.е. базисные функции не соответствуют линейной фазе). Эти преобразования не применимы к приложениям сжатия данных, в которых требуются функции линейной фазы (симметричные), такие как цифровое сжатие изображений.

Для сжатия рисунков (изображений) одна из наиболее производительных методик преобразования с точки зрения производительности R-D - это биортогональное преобразование с перекрытием (LBT). См.S. Malvar, "Biorthogonal and nonuniform lapped transforms for transform coding with reduced blocking and ringing artifacts", IEEE Trans. on Signal Processing, том 46, стр.1043-1053, апрель 1998 г. В отличие от MLT, базисные функции LBT являются симметричными и не являются точно ортогональными (в LBT базисные функции анализа являются ортогональными для базисных функций синтеза, следовательно, условно биортогональными). LBT успешно использовались в приложениях сжатия изображений, но они до сих пор не использовались в сжатии изображений без потерь, поскольку численно-целообратимые структуры были неизвестны.

Обзор блочного основанного на преобразовании кодирования

Кодирование с преобразованием - это методика сжатия, используемая во многих системах сжатия звука, изображений и видео. Несжатое цифровое изображение или видео в типичном случае представляется или захватывается как выборки элементов изображений или цветов в местах в изображении или видеокадре, организованные в двумерную (2D) сетку. Это упоминается как представление в пространственной области изображения или видео. Например, типичный формат для изображений состоит из потока 24-битных выборок элементов цветных изображений, организованных как сетка. Каждая выборка - это число, представляющее цветовые компоненты в месте пикселя сетки в рамках цветового пространства, такого как RGB или YIQ, помимо прочего. Различные системы изображений и видео могут использовать различные цветовые, пространственные и временные разрешения выборки. Также цифровое аудио в типичном случае представляется как дискретизируемый по времени поток звуковых сигналов. Например, типичный формат аудио состоит из потока 16-битных выборок по амплитуде звукового сигнала, взятых с постоянным интервалом времени.

Несжатые цифровые сигналы звука, изображений и видео могут потреблять значительную емкость при хранении и передаче. Кодирование с преобразованием уменьшает размер цифрового аудио, изображений и видео посредством преобразования представления сигнала в пространственной области в представление в частотной области (или другой аналогичной области преобразования) и последующего уменьшения разрешения определенных, в общем, менее воспринимаемых частотных компонентов представления в области преобразования. Это обычно дает в результате гораздо менее воспринимаемое ослабление цифрового сигнала по сравнению с уменьшением цветового или пространственного разрешения изображений или видео в пространственной области или звука во временной области.

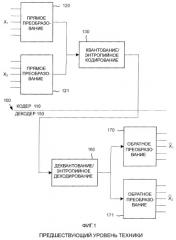
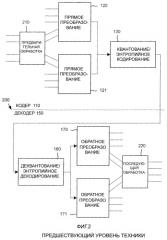
Более конкретно, типичный блочный основанный на преобразовании кодек 100, показанный на фиг.1, делит пиксели несжатого цифрового изображения на двумерные блоки фиксированного размера (X₁,..., X_n), при этом каждый блок, возможно, перекрывается другими блоками. Линейное преобразование 120-121, которое выполняет анализ пространственных частот, применяется к каждому блоку, что преобразует разнесенные выборки в рамках блока к набору коэффициентов частот (или преобразования), обычно представляющих интенсивность цифрового сигнала в соответствующих полосах частот по блочному интервалу. Для сжатия коэффициенты преобразования могут быть выборочно квантованы 130 (т.е. уменьшено их разрешение, например, посредством отбрасывания самых младших битов значений коэффициентов или иного отображения значений в числовом множестве с более высоким разрешением на меньшее разрешение), а также закодированы 130 энтропийным кодированием или кодированием с переменной длиной поля в сжатый поток данных. При декодировании коэффициенты преобразования обратно преобразуются 170-171, чтобы приблизительно восстановить исходный дискретизированный по цвету/пространству сигнал изображения/видео (восстановленные блоки ...).

Блочное преобразование 120-121 может быть задано как математическая операция над вектором x размера N. Более часто операцией является линейное умножение, дающее выход области преобразования y=Mx, где M является матрицей преобразования. Когда входные данные имеют произвольную длину, они сегментируются на N векторов определенной длины, и блочное преобразование применяется к каждому сегменту. Для целей сжатия данных выбираются обратимые блочные преобразования. Другими словами, матрица M является обратимой. В нескольких измерениях (к примеру, для изображения и видео) блочные преобразования в типичном случае реализуются как отдельные операции.

Матричное умножение применяется раздельно вдоль каждого измерения данных (т.е. и строк, и столбцов).

Для сжатия коэффициенты преобразования (компоненты вектора y) могут быть выборочно квантованы (т.е. уменьшено их разрешение, например, посредством отбрасывания самых младших битов значений коэффициентов или иного отображения значений в числовом множестве с более высоким разрешением на меньшее разрешение), а также закодированы энтропийным кодированием или кодированием с переменной длиной в сжатый поток данных.

При декодировании в декодере 150 инверсия этих операций (деквантованию/энтропийное декодирование 160 и обратное блочное преобразование 170-171) применяется на стороне декодера 150, как показано на фиг.1. При восстановлении данных обратная матрица M ^-1 (обратное преобразование 170-171) применяется в качестве множителя к данным области преобразования. При применении к данным области преобразования обратное преобразование приблизительно восстанавливает исходное цифровое мультимедиа временной области или пространственной области.

Во многих приложениях кодирования на основе блочного преобразования преобразование, желательно, является обратимым, чтобы поддерживать кодирование, как с потерями, так и без потерь в зависимости от коэффициента квантования. При отсутствии квантования (обычно представляемого как коэффициент квантования 1), например, кодек, использующий обратимое преобразование, может точно воспроизводить входные данные при декодировании. Тем не менее, требование обратимости в этих приложениях ограничивает выбор преобразований, на основе которых может быть разработан кодек.

Многие системы сжатия изображений и видео, такие как MPEG и Windows Media, помимо прочих, используют преобразования на основе дискретного косинусного преобразования (DCT). DCT, как известно, имеет подходящие энергетические свойства сжатия, что приводит к практически оптимальному сжатию данных. В этих системах сжатия обратное DCT (IDCT) используется в циклах восстановления, как в кодере, так и в декодере системы сжатия для восстановления отдельных блоков изображений. DCT описано в публикации N. Ahmed, T. Natarajan и K.R. Rao "Discrete Cosine Transform", IEEE Transactions on Computers, C-23 (январь 1974), на стр.90-93. Примерная реализация IDCT описана в"IEEE Standard Specification for the Implementations of 8x8 Inverse Discrete Cosine Transform", IEEE Std. 1180-1990, 6 декабря 1990 г.

При сжатии статического изображения (или внутренне закодированного кадра видеопоследовательности) самые распространенные стандарты, такие как MPEG-2, MPEG-4 и Windows Media, разбивают изображение на квадратные мозаичные элементы и применяют блочное преобразование к каждому мозаичному элементу изображения. На коэффициенты преобразования в заданном разделе (общеизвестном как блок) влияют только компоненты необработанных данных в этот блоке. Необратимые операции или операции с потерями на стороне кодера, такие как квантование, обуславливают появления артефактов в закодированном изображении. Эти артефакты не зависят от блоков и создают визуально раздражающий эффект, называемый эффектом блокирования. Также для звуковых данных, когда неперекрывающиеся блоки независимо кодируются с преобразованием, ошибки квантования генерируют разрывы в сигнале на границах блоков при восстановлении звукового сигнала в декодере. Для звука слышен эффект периодических щелчков.

Несколько методик используются, чтобы бороться с эффектом блокирования. Наиболее популярные среди них - это фильтр деблокирования, который сглаживает края внутренних блоков, и пространственная экстраполяция, которая кодирует различия между необработанными входными данными и прогнозированием от краев соседних блоков. Эти методики имеют свои недостатки. Например, подход фильтра деблокирования - это "разомкнутый контур", т.е. процесс прямого преобразования не принимает во внимание тот факт, что деблокирование должно выполняться до восстановления на стороне декодера. Кроме того, обе эти методики с большим объемом вычислений.

Чтобы минимизировать эффект блокирования, могут быть использованы межблочные корреляции. Один способ достижения межблочной корреляции заключается в использовании преобразования с перекрытием, как описано в H. Malvar, "Signal Processing with Lapped Transforms", Artech House, Норвуд, штат Массачусетс, 1992 г. Перекрывающееся преобразование - это преобразование, вход которого распространяется, помимо элементов данных в текущем блоке, на несколько соседних элементов в соседних блоках. Также на стороне восстановления обратное преобразование влияет на все точки данных в текущем блоке, а также на несколько точек данных в соседних блоках.

В случае двумерных (2D) данных перекрывающееся двумерное преобразование - это функция текущего блока, вместе с выбранными элементами блоков слева, вверху, справа, внизу и, возможно, вверху слева, вверху справа, внизу слева и внизу справа. Количество точек данных в соседних блоках, которые используются, чтобы вычислять текущее преобразование, упоминается как перекрытие.

Обзор преобразования с перекрытием, соответствующего пространственной области

Преобразование с перекрытием может быть реализовано в области преобразования в качестве этапа, который объединяет величины областей преобразования после традиционного блочного преобразования. Кроме того, это может быть реализовано в пространственной области посредством стадии предварительной обработки, которая применяется к пикселям в диапазоне перекрытия. Эти две реализации математически связаны и поэтому эквивалентны.

Фиг.2 показывает пример традиционного преобразования с перекрытием соответствующей пространственной области. В показанном примере перекрытие составляет два пикселя, и два пикселя, каждый из двух показанных соседних блоков, предварительно обрабатываются на стадии 210 предварительной обработки. Два предварительно обработанных вывода отправляются каждому из блоков для блочного основанного на преобразовании кодирования кодеком 100, как показано на фиг.1. Инверсия стадии предварительной обработки применяется на стадии последующей обработки (постобработки) 220 после декодирования. С разумным выбором предварительной обработки и блочного преобразования широкий диапазон преобразований с перекрытием может быть реализован.

Ключевое преимущество реализации в пространственной области преобразования с перекрытием состоит в том, что используемый основанный на блочном преобразовании кодек может быть модернизирован с помощью стадии предварительной или последующей обработки, чтобы получать преимущества преобразования с перекрытием, т.е. уменьшенный эффект блокирования и лучшее сжатие, используя структуру используемого кодека. Предварительная обработка 210 и постобработка могут быть представлены как матричное умножение, как показано на фиг.3. Традиционно матрицы предварительной и постобработки являются инверсиями друг друга, т.е. перемноженные матрица предварительной обработки (P _f ) и инверсия или матрица постобработки (P _i) равны единичной матрице I.

Определения

В общем, длина N преобразования - это число коэффициентов преобразования в конкретном блоке преобразования.

Основание K преобразования - это число точек входных данных, которые оказывают влияние на коэффициенты блока преобразования, также - это число точек выходных данных, которые находятся под влиянием каждого коэффициента преобразования посредством процесса обратного преобразования.

Для типичных блочных преобразований, таких как дискретное косинусное преобразование (DCT), длина и основание идентичны. Тем не менее, преобразования с перекрытием (LT) являются важным классом преобразований, для которых основание K больше, чем длина N. Обозначение K x N используется, чтобы отмечать основание и длину преобразования с перекрытием. (Преобразования, для которых K<N, являются расширяющимися и поэтому не используются в сжатии данных.)

В качестве примера 300, LT 310 6x4, показанное на фиг.3, является преобразованием с шестью входами и четырьмя выходами. Поскольку преобразование является обратимым, два входа совместно используются соседними блоками преобразования. Обратное преобразование с перекрытием (ILT) 320 генерирует шесть выходов из своих четырех входов. Точки входных данных рядом с границей блоков (в данном случае одна точка в каждом конце блока) восстанавливаются посредством суммирования соответствующих откликов от двух соседних блоков обратного преобразования.

Ограничения на преобразования с перекрытием, используемые в системах сжатия

В математическом смысле преобразования с перекрытием - это обратимые структуры, когда мы рассматриваем входные и выходные сигналы, а также результаты промежуточных вычислений как действительные числа. Если бесконечная точность может быть достигнута, входные данные могут быть полностью восстановлены из своих коэффициентов преобразования с перекрытием. Тем не менее, бесконечная точность невозможна на практике; для сжатия данных без потерь требование состоит в том, чтобы спроектировать платформу, которая осуществляет операции в отношении целых чисел или с заданной точностью, тем не менее, полностью восстанавливает данные при заданном целочисленном представлении коэффициентов преобразования. Это более строгое условие, чем математическая обратимость, и такое преобразование, упоминаемое в данном документе как преобразование "без потерь". Более того, требуется, чтобы преобразование без потерь было так же эффективным и для сжатия данных (как без потерь, так и с потерями). Эта эффективность может быть измерена посредством энтропии преобразованных данных; чем ниже эта энтропия, тем больше преобразованные данные могут быть сжаты посредством стандартных методик энтропийного кодирования, таких как основанное на контексте арифметическое кодирование или адаптивное кодирование по длинам серий.

Сущность изобретения

В данном документе описаны различные реализации эффективного преобразования с перекрытием, которое обратимо в целочисленной арифметике и может быть использовано в качестве основы системы эффективного сжатия/восстановления данных без потерь.

Может быть показано, что наиболее эффективные структуры преобразования без потерь (т.е. структуры с минимальной энтропией преобразованных данных) требуют, чтобы матрица преобразования была с единичным детерминантом (т.е. детерминант матрицы преобразования равнялся±1). В последующем описании предполагается, что преобразование может быть представлено как матричное умножение, хотя очевидно, что могут быть незначительные нелинейные явления, такие как округление данных. Таким образом, когда мы ссылаемся на детерминант, аспекты усечения и округления не рассматриваются.

Эффективное преобразование с перекрытием реализуется с помощью предварительных фильтров и постфильтров, которые упоминаются в данном документе как "операторы перекрытия". Эта реализация является обратимой и по-прежнему очень эффективной по R-D. Среди других вариантов применения, эти новые операторы перекрытия разрешают реализацию обратимых LBT, которые могут быть использованы для сжатия изображений без потерь. Предварительные фильтры и постфильтры используют обратимые операции. Дополнительно описанные операторы перекрытия включают в себя упрощения для вычислительной эффективности.

Одна реализация операций предварительной и последующей постфильтрации заключается в последовательности плоских преобразований поворота и плоских преобразований с единичным детерминантом масштабирования. Дополнительно плоские повороты и плоские сдвиги имеют реализацию как обратимые операции без потерь, предоставляя в качестве результата оператор обратимого перекрытия.

Типичное применение - это одномерное преобразование с перекрытием 8x4, реализованное с помощью вычислительно эффективных аппроксимаций операторов обратимого перекрытия.

Дополнительные признаки и преимущества станут более явными из последующего подробного описания вариантов осуществления, которое осуществляется со ссылками на прилагаемые чертежи.

Перечень чертежей

Фиг.1 - блок-схема традиционного блочного основанного на преобразовании кодека согласно предшествующему уровню техники.

Фиг.2 - блок-схема преобразования с перекрытием, соответствующего пространственной области, реализованного в качестве операций предварительной и последующей фильтрации в сочетании с блочным основанным на преобразовании кодеком по фиг.1, также согласно предшествующему уровню техники.

Фиг.3 - блок-схема, иллюстрирующая пару преобразования с перекрытием и обратного преобразования с перекрытием на одномерных данных.

Фиг.4 - блок-схема алгоритма кодера, основанного на преобразовании с перекрытием, использующем оператор обратимого перекрытия.

Фиг.5 - блок-схема декодера, основанного на преобразовании с перекрытием.

Фиг.6 - блок-схема, иллюстрирующая пару преобразования с перекрытием и обратного преобразования с перекрытием на одномерных данных, использующую операции предварительной и последующей фильтрации (или оператор обратимого перекрытия) совместно с блочным преобразованием.

Фиг.7 - сигнальный ориентированный граф, иллюстрирующий структуру предварительного фильтра или постфильтра линейной фазы для использования в качестве оператора обратимого перекрытия в преобразовании с перекрытием по фиг.6.

Фиг.8 - сигнальный ориентированный граф масштабирования без потерь в качестве четырех этапов лифтинга для использования в операторе обратимого перекрытия.

Фиг.9 - сигнальный ориентированный граф масштабирования без потерь в качестве пяти этапов лифтинга для использования в операторе обратимого перекрытия.

Фиг.10 - сигнальный ориентированный граф каскадного двухточечного масштабирования, применяемого к матрице большей возможности, чтобы реализовать масштабирование без потерь с единичным детерминантом.

Фиг.11 - сигнальный ориентированный граф оператора обратимого перекрытия (или предварительного фильтра/постфильтра), имеющего структуру, показанную на фиг.7, и использующего масштабирование без потерь с единичным детерминантом по фиг.10.

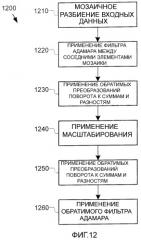
Фиг.12 - блок-схема алгоритма работы оператора обратимого перекрытия по фиг.11.

Фиг.13 - сигнальный ориентированный граф, иллюстрирующий пример реализации обратимого преобразования с перекрытием, использующего оператор обратимого перекрытия по фиг.11.

Фиг.14 - график импульсной характеристики коэффициента постоянного тока (ДС коэффициента) примерного преобразования с перекрытием по фиг.13.

Фиг.15 - блок-схема подходящей вычислительной среды для реализации блочного основанного на преобразовании кодека с помощью усовершенствованного преобразования с перекрытием в пространственной области по фиг.4 и 5.

Подробное описание изобретения

Последующее описание относится к системе сжатия или кодеку цифрового мультимедиа, который использует оператор обратимого перекрытия для преобразования с перекрытием. В целях иллюстрации, вариантом осуществления системы сжатия, содержащей оператор обратимого перекрытия, является система сжатия изображений или видео. Альтернативно оператор обратимого перекрытия также может быть включен в системы сжатия или кодеки для других двумерных данных. Оператор обратимого перекрытия не требует, чтобы система сжатия цифрового мультимедиа кодировала сжатые цифровые мультимедийные данные в конкретном формате кодирования.

1. Кодер/декодер

Фиг.4 и 5 - это обобщенная диаграмма процессов, используемых в репрезентативном двумерном (2D) кодере 400 и декодере 500 данных, основанных на преобразовании с перекрытием, использующем оператор обратимого перекрытия. Схемы представляют обобщенную или упрощенную иллюстрацию использования и применения данного оператора обратимого перекрытия в системе сжатия, включающей кодер и декодер двумерных данных. В альтернативных кодерах, основанных на этом операторе обратимого перекрытия, дополнительное или меньшее число процессов, чем проиллюстрировано в репрезентативном кодере и декодере, может быть использовано для сжатия двумерных данных. Например, некоторые кодеры/декодеры могут также включать в себя цветовое преобразование, форматы цветов, масштабируемое кодирование, кодирование без потерь, режимы макроблоков и т.д. Система сжатия (кодер и декодер) может предоставлять кодирование двумерных данных без потерь и/или с потерями, в зависимости от квантования, которое может быть основано на параметре квантования, варьирующемся от соответствующего режима без потерь до соответствующего режима с потерями.

Кодер 400 двумерных данных генерирует сжатый поток 420 битов, который является более компактным представлением (для типичного ввода) двумерных данных 410, представляемых в качестве входа кодеру. Например, вводом двумерных данных может быть изображение, кадр видеопоследовательности или другие данные, имеющие два измерения. Кодер двумерных данных разбивает 430 входные данные на макроблоки, которые имеют размер 16x16 пикселей в данном репрезентативном кодере. Кодер двумерных данных дополнительно разбивает макроблок на блоки 432 4x4. Оператор 440 "прямого перекрытия" применяется к каждому краю между блоками, после чего каждый блок 4x4 преобразуется с помощью блочного преобразования 450. Этим блочным преобразованием 450 может быть обратимое безразмерное двумерное преобразование, описанное Srinivasan в Патентной заявке США, озаглавленной "Improved Reversible Transform For Lossy And Lossless 2-D Data Compression", поданной одновременно с данной заявкой, раскрытие которой включено в данный документ посредством ссылки. Альтернативно дискретное косинусное преобразование или другие блочные преобразования могут быть использованы с оператором обратимого перекрытия, описанным в данном документе. Вслед за упомянутым преобразованием ДС коэффициент 460 каждого блока преобразования 4x4 подвергается аналогичной цепочке обработки (разбиение, прямое перекрытие, за которым следует блочное преобразование 4x4). Результирующие ДС коэффициенты преобразования тока и АС коэффициенты (коэффициенты переменного тока) преобразования квантуются 470, кодируются 480 энтропийным кодированием и пакетируются 490.

Декодер выполняет обратный процесс. На стороне декодера биты коэффициентов преобразования извлекаются 510 из своих соответствующих пакетов, из которых сами коэффициенты декодируются 520 и деквантуются 530. ДС коэффициенты 540 регенерируются посредством применения обратного преобразования, и в отношении плоскости ДС коэффициентов выполняется «обращенное перекрытие» с помощью подходящего сглаживающего оператора, применяемого по краям блока постоянного тока. В дальнейшем все данные регенерируются посредством применения обратного преобразования 550 4x4 к ДС коэффициентам, и АС коэффициенты 542 декодируются из потока битов. Наконец, края блока в плоскостях результирующих изображений фильтруются 560 на основе обращенного перекрытия. Это генерирует восстановленный вывод двумерных данных.

2. Преобразование с перекрытием, реализованное с помощью операторов перекрытия

Более обобщенно, оператор 440 перекрытия и блочное преобразование 450 кодера 400 (фиг.4) является примером обширного класса преобразований 600 с перекрытием, которые могут быть разложены на операцию 610 предварительной фильтрации, за которой следует блочное преобразование 620 данных, как проиллюстрировано на фиг.6. Фиг.6 иллюстрирует обобщенный пример такого разложения преобразований с перекрытием. В проиллюстрированном случае преобразование с перекрытием 310 6x4, показанное на фиг.3, разлагается на стадии операции 610 предварительной фильтрации и блочного преобразования 620. Операция 610 предварительной фильтрации и блочное преобразование 620 равномерно применяются относительно точек данных. В данном проиллюстрированном примере преобразования 600 с перекрытием 6x4 каждый предварительный фильтр - это преобразование с длиной 2 точек данных, переходящих на соседние блоки. На стороне декодера постфильтр 640 применяется после обратного блочного преобразования вдоль границ блоков. Также для общего случая KxN предварительный фильтр применяется к (K-N)/2 точкам данных каждого блока, соседствующего с границей блока.

Для обратимости предварительный фильтр 610 и постфильтр 640 являются инверсиями друг друга. Для реализации преобразования с перекрытием без потерь, тем не менее, этого условия недостаточно. Это дополнительно ограничивает предварительные фильтры и постфильтры 610, 640, которые также должны быть преобразованиями без потерь, помимо блочного (базового) преобразования 620, которое должно быть реализовано способом без потерь. DCT может быть реализовано способом без потерь, используя лестничные, решетчатые или основанные на лифтинге (преобразовании, основывающемся на сокращении числа выборок за счет удаления коррелирующих значений при сокращении определенных скалярных характеристик) способы, помимо прочего. См., к примеру, A. A. M. L. Brackens и A. W. M. van den Enden, "New networks for perfect inversion and perfect reconstruction", IEEE J. Selected Areas Communications, том 10, номер l, 1992 г.; и I. Daubechies и W. Sweldens, "Factoring wavelet transform into lifting steps", J. Fourier Anal. Appl., т.4, стр.247-269, 1998. Обратимое безразмерное двумерное преобразование также описано Srinivasan в Патентной заявке США, озаглавленной "Improved Reversible Transform For Lossy And Lossless 2-D Data Compression", поданной одновременно с данной заявкой и включенной в данный документ посредством ссылки. Также известны основанные на лифтинге обратимые аппроксимации к DCT в одном измерении. См., к примеру, J. Liang и T. D. Tran, "Fast multiplierless approximations of the DCT with the lifting scheme", IEEE Trans. Signal Processing, т.49, стр.3032-3044, декабрь 2001 г. Эффективная обратимость дополнительно требует, чтобы оба этапа, т.е. предварительная/последующая фильтрации и блочное преобразование, были с единичным детерминантом.

3. Оператор обратимого перекрытия

Оператор эффективного обратимого перекрытия для использования в качестве предварительного фильтра 610 (фиг.6) преобразования 600 с перекрытием без потерь, на котором основан кодер 400/декодер 500 (фиг.4 и 5), может быть реализован в качестве предварительного фильтра линейной фазы, который представлен в виде в структуры 700, показанной на фиг.7. Инверсия данного предварительного фильтра (т.е. постфильтр 640) также имеет такую же структуру, но с другими коэффициентами.

Данная структура 700 фильтра линейной фазы имеет несколько ортогональных компонентов, в том числе перекрестную схему 710 Адамара на своем входе и выходе. Внутренние стрелки в проиллюстрированной схеме 710 Адамара означают отрицание на данной схеме. Структура 700 дополнительно включает в себя ортогональные матрицы U1, U2, V1 и V2. Эти компоненты могут быть реализованы способом без потерь посредством использования решетчатых/основанных на лифтинге способов.

Помимо этого, структура 700 имеет ненулевые масштабные коэффициенты S ₁ -S _M . Ограничение по единичности детерминанта подразумевает, что . Когда все масштабные коэффициенты равны ±1, предварительные фильтры/постфильтры могут быть реализованы в качестве преобразования без потерь, где матрицы компонентов U1, U2, V1 и V2 реализованы как этапы решетки/лифтинга без потерь. Тем не менее, когда масштабные коэффициенты не равны все±1, реализация без потерь остается сложной задачей, которая решается и обсуждается подробнее далее.

С помощью данной структуры 700 предварительного фильтра линейной фазы проблема реализации пары предварительного фильтра/постфильтра сокращается до трех следующих этапов:

1. Разложение фильтра F в следующую форму для ортогональных матриц U1, U2, V1 и V2:

(1)

где I - это единичная матрица,

2. Получение реализаций без потерь для U1, U2, V1 и V2; и

3. Получение реализаций без потерь для матрицы масштабирования.

Что касается этапа 1, первая и последняя матрицы в правой части, которые задают двухточечные преобразования Адамара, включают коэффициент 1/2 в некоторых членах, чтобы сделать эти стадии с единичным детерминантом. Прочее реорганизуется в блочную диагональную форму с помощью двух блоков, каждый из половины линейных измерений F. Разложение по сингулярным значениям (или SVD) каждого блока предоставляет ортогональные матрицы U1, U2, V1 и V2, а также масштабы.

Реализации без потерь матриц компонентов могут быть получены на этапе 2 с помощью стандартных основанных на лифтинге методик, таких как описанные A. A. M. L. Bruekens и A. W. M. van den Enden, "New networks for perfect inversion and perfect reconstruction", IEEE J. Selected Areas Communications, том 10, номер 1, 1992 г.

Реализация без потерь матрицы масштабирования на этапе 3 разрешается следующим образом. Для простоты допустим, что мы имеем конкретный компонент с двумя входами и двумя выходами, который является (a) без потерь и (b) реализует масштабирование посредством s (0<s<1) для первого компонента и посредством 1/s для второго компонента (другие случаи могут быть получены посредством перемены знака одного или обоих выходных сигналов). Другими словами, мы имеем отношение входа-выхода, заданное как:

(2)

Детерминант матрицы преобразования в (2) - это s/s=1. Данная матрица может быть реализована в процедуре 800 с четырьмя этапами лифтинга или процедуре 900 с пятью этапами лифтинга, показанных на фиг.8 и 9. Мы обычно аппроксимируем все этапы лифтинга в форму y=(a.x+r)>>b, где x - это вход, y - это выход, a, b и r - это целые числа, и r используется для контроля ошибок округления, чтобы получить уменьшенную на деление целочисленную реализацию. Преобразование, заданное уравнением (2), упоминается в данном документе как с единичным детерминантом преобразование масштабирования, сокращенно преобразование масштабирования.

Интересно, что преобразование масштабирования тесно связано с операцией сдвига, как задано ниже:

(3)

При ограничении a ² -b ² =1×(a>0, b≥0) операция сдвига имеет единичный детерминант и может быть реализована с помощью трех этапов лифтинга:

Следовательно,

При этом коэффициенты масштабирования 1/2 и 2 в матрицах, размещенных слева и справа относительно матрицы сдвига, распространяются на этапы лифтинга со сдвигом, и последний этап лифтинга первой матрицы объединяется с первым этапом лифтинга со сдвигом, тогда как первый этап лифтинга последней матрицы объединяется с первым этапом лифтинга со сдвигом. Реализация в пять этапов в качестве процедуры 900 преобразования масштабирования, показанная на фиг.9, основана на уравнении (5). Упрощения в структуре могут быть возможны посредством отмены операций инверсии, при возможности, между тремя группами в уравнении, т.е. схемами Адамара, ортогональными матрицами и операциями масштабирования (которые, в свою очередь, могут быть разложены в операции Адамара и сдвига).

Более конкретно, эффективная матрица преобразования данной реализации с четырьмя этапами лифтинга масштабирования без потерь в качестве процедуры - это

где c ²=1-s ². С другой стороны, эффективная матрица преобразования реализации с пятью этапами лифтинга в процедуре 900 - это

где c ² =1-s ² .

Хотя процедура 800 масштабирования, показанная на фиг.8, имеет меньше на один этап лифтинга, чем на фиг.9, вторая процедура 900 имеет только три этапа нетривиального лифтинга, в отличие от четырех в первой. По причинам, указанным в параграфе выше, первый или последний этап тривиального лифтинга на фиг.9 могут быть объединены с предшествующим или последующими этапами преобразования (например, со схемой 710 Адамара на любом конце фиг.7) при определенных условиях (например, когда U1, U2 и V1 - единичные).

Процедура масштабирования легко может быть распространена на более крупные матрицы. Это проиллюстрировано на фиг.10, где M, возможно, различных масштабных коэффициентов s ₁-s_M применяются к M путем данных в качестве каскада 1000 преобразований масштабирования. Чтобы достичь этого обратимым способом, в общем, требуется M-1 обратимых преобразований масштабирования.

Один полезный особый случай - это когда M масштабных коэффициентов s ₁ -s_M группируются в M/2 групп формы (s, 1/s). В этом случае требуется только M/2 обратимых преобразований масштабирования. Один пример - это s ₁ =s ₂ =...=s _M/2 =s, а s _M/2+1 =s _M/2+2 =...=s _M =1/S. Предпочтительный способ группирования - сохранять симм