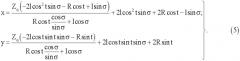Способ измерения диаметра объектов цилиндрической формы с направленно отражающей поверхностью

Способ измерения диаметра объектов цилиндрической формы с направленно отражающей поверхностью

Иллюстрации

Показать все

Реферат

Предлагаемое техническое решение относится к измерительной технике и может быть использовано в приборостроении, светотехнике, медицине, термометрии и т.д. для измерения диаметра объектов с цилиндрической направленно отражающей поверхностью, например металлических и стеклянных трубок, капилляров и т.п.

Известно устройство (авторское свидетельство СССР №1534301, 1973 г.), содержащее источник излучения, передающую и принимающую оптические системы, блок обработки информации, вход которого подключен к выходам линейных фотоприемников.

Данное устройство обладает следующими недостатками: невозможность измерять диаметр непрозрачных изделий, а также то, что о геометрических параметрах судят по точкам, спроецированным на линейном фотоприемнике, исходя из того, что эти точки получены при отражении луча, лежащего в одной плоскости с геометрической осью объекта измерения (опорной плоскости), и расчет производят как для плоскопараллельных пластинок. В реальных условиях, особенно в процессе производства, неизбежны колебания объекта измерения, которые приводят к смещению луча от опорной плоскости, что, в свою очередь, приводит к снижению точности измерений.

Известно устройство (авторское свидетельство СССР №1775598, 1992 г.), содержащее лазер, оптическую систему, светоделитель, разделяющий пучок излучения лазера на два пучка, два отражательных элемента, которые обеспечивают одновременное облучение объекта измерения под разными углами, и два линейных фотоприемника с видеоусилителями, соединенными с вычислительными блоками.

Данное устройство имеет следующие недостатки: наличие двух фотоприемников, что усложняет сборку и юстировку оптической системы устройства, невозможность измерять диаметр непрозрачных изделий. Кроме того, данное устройство не учитывает поперечные колебания объекта измерения, которые неизбежно возникают в процессе производства и приводят к уменьшению точности измерения.

Техническая задача, решаемая предлагаемым способом, состоит в повышении точности измерения геометрических параметров объектов за счет уменьшения влияния колебания объекта измерения в поперечной плоскости.

Поставленная задача решается тем, что в известном способе измерения диаметра объектов с цилиндрической направленно отражающей поверхностью, заключающемся в том, что направляют пучок световых лучей под фиксированным углом к оси объекта измерения, регистрируют след отраженных лучей в плоскости анализа, согласно изобретению след отраженных лучей регистрируют на плоском экране, осуществляют первичную обработку следа отраженных лучей при помощи видеодатчика с двухкоординатным фотоприемником, после чего выполняют компьютерную обработку оцифрованного сигнала, определяя при этом координаты точек x_i, у_i на следе отраженных лучей в окрестности экстремума, и вычисляют диаметр объекта по формуле

,

где x_i, у_i - координаты точек кривой-отображения, m - количество точек, а=(Z_q-lcosσ)·tgσ (l - длина осевого луча, σ - угол наклона плоскости, в которой лежат падающие на поверхность лучи к оси цилиндра), Z_q - расстояние от точки, из которой выходят до экрана.

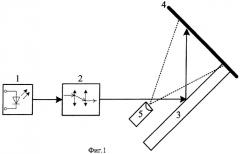
Сущность изобретения поясняется чертежами, где на фиг.1 представлена структурная схема устройства, на фиг.2 - схема, иллюстрирующая способ измерения, на фиг.3 - кривая, создаваемая на экране отраженным от цилиндрической поверхности пучком лучей, на фиг.4 - схема, поясняющая выбор параметров уравнения, аппроксимирующего кривую на экране.

Предлагаемый способ может быть реализован на устройстве, содержащем осветитель, состоящий из полупроводникового лазера 1 и анаморфотной телескопической оптической системы 2; осветитель формирует плоский пучок световых лучей, который падает на исследуемую цилиндрическую поверхность 3. Отраженные лучи падают на экран 4, где и образуют след отраженного пучка, который является кривой-отображением исследуемой поверхности. При помощи видеодатчика 5 первичная информация о форме и размерах этой кривой передается в компьютер 6, где обрабатывается по заданному алгоритму, который включает в себя обработку изображения и определение координат точек кривой-отображения.

Способ измерения основан на том, что в отраженном пучке каждому падающему лучу будет соответствовать «свой» отраженный луч. Если на пути отраженных лучей поставить экран, то каждый отраженный луч оставит на нем след. Этот след является отображением соответствующей точки поверхности на плоскости. Между координатами этих точек существует однозначная взаимосвязь, позволяющая по известным координатам одной точки находить координаты другой. Известен метод отображений, применяемый в светотехнике [1] для решения прямой задачи, - определения параметров световых пучков, формируемых оптическими устройствами световых приборов. Предлагаемый способ относится к измерительной технике и позволяет решать обратную задачу - находить геометрические параметры объекта по его отображению.

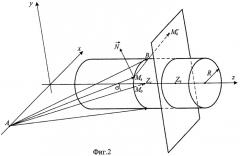
Схема, иллюстрирующая данный метод, приведена на фиг.2. Световые лучи выходят из точки А и падают на поверхность цилиндра, описывающего поверхность объекта измерения, радиуса R, ось которого совмещена с осью z декартовой системы координат. Плоскость, в которой лежат лучи, наклонена к оси z и, следовательно, образующим цилиндра под углом σ. Пусть длина луча равна l, тогда уравнение плоскости, проходящей через точки А, В и Z_c, и уравнение исследуемой цилиндрической поверхности могут быть записаны в следующем виде:

откуда получают, что линия пересечения цилиндра с плоскостью ABZ_C представляет собой эллипс и описывается параметрическим уравнением

Здесь параметр t представляет собой угол между положительным направлением оси х и радиус-вектором текущей точки сечения. При этом если лучи в пучке параллельны (l=∞), то параметр t может принимать значения от π/2 до 3π/2); при уменьшении l этот интервал «сужается».

Координаты плавающей точки М_k на кривой сечения в выбранной декартовой системе также определяются уравнениями (2). Вектор определяет падающий на цилиндрическую поверхность луч. Пусть отраженный луч пересекает экран (плоскость, определяемую уравнением z=Z_q) в точке , которая, как было отмечено выше, является отображением точки M_k на плоскости.

Для нахождения вектора , определяющего отраженный от цилиндрической поверхности луч, используют закон отражения в векторной форме:

где - единичный вектор нормали , координаты которого

(x_N, у_N, z_N) находят в результате дифференцирования уравнения поверхности цилиндра.

При известных координатах вектора падающего луча и единичного вектора нормали с помощью уравнения (3) находят координаты вектора отраженного луча . Этот вектор определяет направление прямой , уравнение которой записывают в виде

Решая совместно уравнение прямой (4) и плоскости (z=Z_q), находят координаты точки :

Найденные с учетом переноса начала системы координат в точку Z_q уравнения (5) описывают плоскую кривую, образованную пересечением отраженных лучей с плоскостью. Эта кривая представляет собой геометрическое место следов лучей, отраженных на цилиндрической поверхности, и, следовательно, является отображением исследуемого сечения на плоскости координат х, у.

Применение параметрического уравнения (5) для решения обратной задачи - восстановления оригинала - вызывает значительные затруднения. В связи с этим возникает необходимость его аппроксимации.

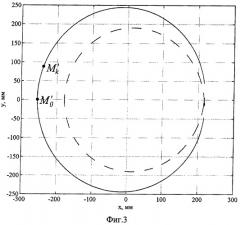
В общем случае эта кривая имеет две петли (фиг.3) и по виду напоминает конхоиду окружности. Интерес представляет только левая часть внешней петли (показана сплошной линией), где параметр t принимает допустимые значения. Часть кривой, показанная пунктиром, соответствует лучам, отраженным от внутренней поверхности бесконечно тонкого прозрачного цилиндра. Изложенное позволяет аппроксимировать параметрическое уравнение (5) уравнением конхоиды окружности:

где параметр а=(Z_q-lcosσ)·tgσ.

Геометрический смысл уравнения (6) проиллюстрирован на фиг.4.

При назначении параметров уравнения (6) учитывают, что при выбранной аппроксимации в связи с изменением ориентации системы координат в отраженном пучке внешняя петля кривой располагается правее внутренней. Предлагаемая аппроксимация при этом обладает следующими достоинствами: 1) начало координат лежит на оси цилиндра, что дает возможность контролировать его положение в процессе измерения; 2) диаметр цилиндрической поверхности выражается в явном виде через координаты любой точки на отображении исследуемого сечения:

Данное уравнение и положено в основу предлагаемого метода измерения диаметра цилиндрической поверхности, который заключается в нахождении на экране координат точек отображения кривой сечения цилиндрической поверхности плоским пучком световых лучей и вычислении диаметра по формуле (7).

Для повышения точности значение диаметра вычисляют для относительно большого количества точек на кривой в окрестности точки экстремума (t=π) и усредняют по формуле

где i - номер точки на кривой, m - количество точек.

Предлагаемый способ измерения диаметра объектов цилиндрической формы с направленно отражающей поверхностью позволяет повысить точность измерения за счет применения нового метода получения измерительной информации об объекте путем отображения на плоскости его сечения плоским пучком лучей и компьютерной обработки этого отображения.

Способ может быть использован для измерения диаметра объектов цилиндрической формы с направленно отражающей поверхностью, например металлических и стеклянных трубок, капилляров и т.п.

Экспериментальные исследования устройства, реализованного на основе предложенного метода, подтверждают возможность его применения для решения практических задач - при измерении диаметра трубок-колб для люминесцентных ламп была получена воспроизводимость результатов не хуже ±1% и относительная погрешность не хуже ±2%.

Литература

1. Трембач В.В. Световые приборы. - М.: Высш. шк., 1990. - 463 с.

Способ измерения диаметра объектов с цилиндрической направленно отражающей поверхностью, заключающийся в том, что направляют плоский пучок выходящих из точки световых лучей под фиксированным углом к оси цилиндрической поверхности объекта измерения, совмещенной с осью z декартовой системы координат, регистрируют след отраженных от поверхности объекта лучей, отличающийся тем, что регистрацию следа отраженных лучей осуществляют на плоском экране, плоскость которого определяется уравнением z=Z_q, где Z_q - расстояние от точки, из которой выходят световые лучи, до экрана, при помощи видеодатчика с двухкоординатным фотоприемником получают первичную информацию о форме и размерах кривой, являющейся геометрическим местом следов отраженных лучей, передают ее в компьютер, выполняют компьютерную обработку оцифрованного сигнала, при этом переносят начало декартовой системы координат в точку Z_q, определяют координаты точек x_i, у_i на указанной кривой в окрестности ее экстремума и вычисляют диаметр объекта по формуле где i - номер точки на кривой;m - количество точек;a=(Z_q-lcosσ)·tgσ;l - расстояние от точки, из которой выходят световые лучи, до оси z;σ - угол наклона плоскости, в которой лежат падающие на поверхность лучи к оси цилиндрической поверхности объекта измерения.