Способ разделения джиттера сигнала данных

Способ разделения джиттера сигнала данных

Иллюстрации

Показать все

Реферат

Изобретение относится к области анализа сигналов, а именно к анализу джиттера цифровых тактируемых сигналов и разложению джиттера на его составляющие.

Джиттером (фазовым дрожанием) называется отклонение показательных участков цифрового сигнала (например, фронтов) от своих идеальных положений во времени [Рекомендация МСЭ-Т О.172]. В цифровых системах связи джиттер проявляется в виде изменений местоположения фронтов цифрового сигнала во времени, что приводит к рассинхронизации и, как следствие, к искажению передаваемой информации.

Общий джиттер может быть разделен на случайный и детерминированный джиттер, состоящий из периодического джиттера и джиттера, зависящего от данных. Джиттер, зависящий от данных, в свою очередь может быть разделен на межсимвольную интерференцию и искажение коэффициента заполнения импульсной последовательности. Случайный джиттер обусловлен шумовыми процессами, происходящими во всех полупроводниках и компонентах. Предполагается, что этот джиттер подчиняется распределению Гаусса (нормальному распределению) [«Measuring Jitter in Digital Systems», Agilent Technologies Inc., Application Note 1448-1, June 1, 2003; http://cp.literature.agilent.com/litweb/pdf/5988-9109EN.pdf], является теоретически неограниченным и характеризуется средним значением и среднеквадратическим отклонением. Периодический джиттер описывает периодические изменения положений фронтов импульсов передаваемого сигнала во времени. Главными причинами периодического джиттера являются паразитная модуляция сигнала гармониками питающего напряжения, помехи от местных радиостанций или от переключений в сильноточных сетях. Джиттер, зависящий от данных, зависит от передаваемой по исследуемой линии связи битовой последовательности. Детерминированный джиттер имеет ограниченный размах своих значений.

Джиттер является одной из основных проблем при проектировании устройств цифровой электроники, в частности цифровых интерфейсов. Исследование компонентов джиттера необходимо при анализе работоспособности, оценке надежности и поиске неисправностей исследуемой цифровой системы.

Для разложения джиттера на составляющие компоненты используют различные методы, основанные как на статистической обработке значений джиттера во временной области, так и на спектральном представлении джиттера с использованием дискретного преобразования Фурье (ДПФ).

Однако сигнал данных может содержать идущие подряд логические нули или единицы, которые при кодировании, например, линейным кодом NRZ (Non-Return-to-Zero) не вызывают переходов значений исследуемого сигнала. Поэтому измерить значение ошибки временного интервала (отклонения фронта импульса линейного кода от своего идеального положения) между повторяющимися логическими символами невозможно. В моменты отсутствия смены состояний входного сигнала данных появляются неизвестные значения ошибок временных интервалов. Их наличие не позволяет напрямую использовать спектральный метод разделения джиттера на компоненты, так как для последовательности с неизвестными значениями нельзя выполнить ДПФ.

Известен способ разделения джиттера случайной последовательности данных по патенту US 7254168 В2 от 07.08.2007, заключающийся в измерении последовательности ошибок временных интервалов, оценке джиттера, зависящего от данных, устранении джиттера, зависящего от данных, из функции ошибок временных интервалов и разделении случайного и периодического джиттера спектральным методом на основе ДПФ. Недостатком данного способа является низкая точность оценки периодического и случайного джиттера. Недостаток обусловлен восстановлением неизвестных значений в последовательности ошибок временных интервалов путем использования интерполяции по ближайшим известным значениям с последующим применением спектрального метода разделения случайного и периодического джиттера.

Известен способ спектрального измерения джиттера последовательности данных по патенту US 6832172 В2 от 14.12.2004, заключающийся в измерении последовательности ошибок временных интервалов; вычислении спектра общего джиттера с помощью прямого ДПФ; спектральном разделении случайного и детерминированного джиттера; дальнейшем спектральном разделении детерминированного джиттера на периодический джиттер и джиттер, зависящий от данных; выполнении обратного ДПФ спектральных пиков, отнесенных к компонентам детерминированного джиттера; оценке параметров периодического джиттера и джиттера, зависящего от данных; оценке среднеквадратического отклонения значений случайного джиттера на основе спектральной плотности мощности случайного джиттера. Недостатком данного способа также является низкая точность оценок составляющих общего джиттера из-за восстановления неизвестных значений в последовательности ошибок временных интервалов путем использования интерполяции по ближайшим известным значениям.

Наиболее близким, принятым за прототип, является способ разделения джиттера сигнала с использованием многократного захвата по патенту US 6898535 B2 от 24.05.2005, заключающийся в том, что сохраняют входной сигнал в виде сигнальных векторов, формируют функцию исходной структуры данных первого сигнального вектора, вычисляют последовательность ошибок временных интервалов для каждого последующего сигнального вектора, усредняют последовательность ошибок временных интервалов, вычисляют параметры джиттера, зависящего от данных, устраняют джиттер, зависящий от данных, из последовательности ошибок временных интервалов, интерполируют неизвестные значения по ближайшим известным, выполняют прямое ДПФ, вычисляют усредненный спектр ошибок временных интервалов, формируют массив частот F_p, соответствующий частотам пиковых значений амплитуд в усредненном спектре ошибок временных интервалов, вычисляют модифицированный спектр периодического джиттера на частотах F_p, вычисляют временную последовательность периодического джиттера путем обратного преобразования Фурье от модифицированного спектра периодического джиттера, вычисляют гистограмму временной последовательности периодического джиттера, определяют размах значений периодического джиттера по гистограмме, вычисляют усредненную спектральную плотность мощности функции ошибок временных интервалов, вычисляют модифицированный спектр случайного джиттера, выполняют обратное преобразование Фурье от модифицированного спектра случайного джиттера, вычисляют среднеквадратическое отклонение значений случайного джиттера, принимают решение о дальнейшем усреднении результатов. Недостатком данного способа является низкая точность оценки составляющих общего джиттера за счет восстановления неизвестных значений в последовательности ошибок временных интервалов путем использования линейной интерполяции по ближайшим известным значениям.

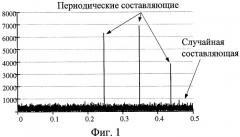
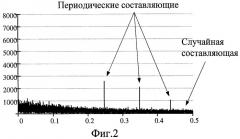
Использование интерполяции по ближайшим известным значениям для восстановления неизвестных значений в последовательности ошибок временных интервалов с последующим вычислением спектра с помощью ДПФ приводит к искажению получаемых результатов. Если некоторые имеющиеся данные используются для оценки пропущенных значений, результирующее среднее значение смещается в пользу данных, используемых для оценки. Так, на фиг.1 изображен амплитудный спектр известной последовательности ошибок временных интервалов, в которой присутствуют случайная и три периодические составляющие. Из известной последовательности ошибок временных интервалов случайным образом (с вероятностью 0,5) удалены некоторые значения, которые затем линейно интерполированы согласно прототипу. Амплитудный спектр ошибок временных интервалов в результате интерполяции представлен на фиг.2. Из сравнения спектров на фиг.1 и фиг.2 видно, что применение интерполяции неизвестных значений по ближайшим известным искажает спектр последовательности ошибок временных интервалов в сторону нижних частот с подавлением амплитуд высокочастотных составляющих. Такое искажение спектра ведет к ухудшению точности оценивания компонентов общего джиттера при использовании спектрального метода разделения.

Техническим результатом, на достижение которого направлено изобретение, является повышение точности оценивания компонентов общего джиттера сигнала данных при использовании спектрального метода разделения.

Указанный технический результат достигается тем, что неизвестные значения в последовательности ошибок временных интервалов сначала заменяются нулевыми значениями, после чего выполняется ДПФ, находятся пиковые значения амплитудного спектра последовательности ошибок временных интервалов, остальным значениям составляющих спектра присваиваются нулевые значения, выполняется обратное ДПФ, полученная модифицированная временная последовательность усиливается в раз, где N - длина сигнального вектора, а

N_Δ - количество знакоперемен в текущем сигнальном векторе. В результате этих действий формируется модифицированная последовательность ошибок временных интервалов, содержащая только периодические составляющие. В исходной последовательности ошибок временных интервалов неизвестные значения заменяют на соответствующие значения из модифицированной последовательности ошибок временных интервалов, после чего выполняют разделение случайного и периодического джиттера с помощью спектрального метода.

Заявленное изобретение поясняется следующими чертежами:

фиг.1 - амплитудный спектр известной последовательности ошибок временных интервалов;

фиг.2 - амплитудный спектр линейно интерполированной последовательности ошибок временных интервалов согласно прототипу;

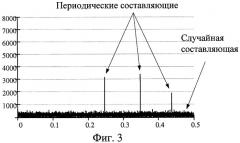
фиг.3 - амплитудный спектр восстановленной последовательности ошибок временных интервалов согласно настоящему изобретению;

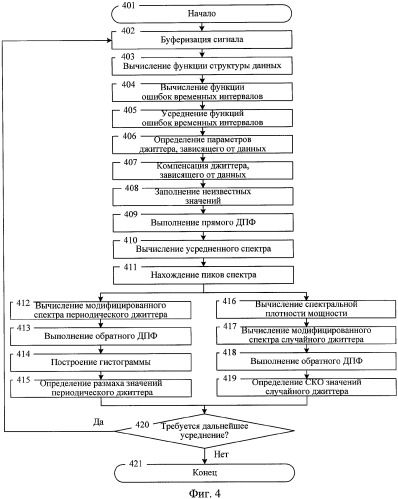
фиг.4 - блок-схема способа разделения джиттера случайного сигнала данных согласно изобретению;

фиг.5 - блок-схема заполнения неизвестных значений функции ошибок временных интервалов согласно изобретению;

фиг.6 - результаты сравнения оценок параметров периодического и случайного джиттера согласно прототипу и предлагаемому способу.

Для повышения точности оценивания компонентов общего джиттера сигнала данных согласно предлагаемому способу выполняют следующие операции. В блоке 402 входной сигнал данных сохраняют (буферизируют) в промежуточной памяти в виде сигнальных векторов x определенной длины N. Для каждого сигнального вектора в блоке 403 вычисляют функцию d структуры данных, представляющую собой последовательность логических нулей и единиц, содержащихся в сохраненном сигнальном векторе х. Значения функции d определяют из уровня входного сигнала x в одной или нескольких точках на протяжении длительности посылки одного логического символа. Далее сохраненный сигнальный вектор x поступает в блок 404 вычисления ошибок временных интервалов, в котором определяют отклонение значащих участков сигнала от своих идеальных положений во времени. Идеальные положения значащих участков могут быть определены как из самого входного сигнала, так и по внешнему опорному сигналу. Получившуюся последовательность отклонений обозначают как первую функцию у ошибок временных интервалов для текущего сигнального вектора х. Так как логические символы (нули и единицы) во входном сигнале могут повторяться, то для таких временных интервалов не будет смены состояний во входном сигнале, а следовательно, первая функция у ошибок временных интервалов на этих временных интервалах будет иметь неопределенные значения. Для первого сигнального вектора функцию d структуры данных фиксируют. Для последующих сигнальных векторов производят временной сдвиг функции d структуры данных для выравнивания по оси времени с функцией d структуры данных первого сигнального вектора. Функция ошибок временных интервалов может быть получена из сдвинутого по времени входного сигнала или из исходного сигнала и сдвинутого по времени первого сигнального вектора. В блоке 405 вычисляют функцию y' усредненной ошибки временных интервалов путем вычисления скользящего среднего между функциями у ошибок временных интервалов соседних сигнальных векторов. Для вычисления функции y' может быть использовано скользящее среднее с экспоненциальными, линейными или другими весами. Далее в блоке 406 определяют параметры джиттера, зависящего от данных. Сначала вычисляют среднее значение а1 функции y' для моментов времени, соответствующих передним фронтам входного сигнала, затем среднее значение а2 функции y' для моментов времени, соответствующих задним фронтам входного сигнала. Разница значений a1 и a2 соответствует величине искажения коэффициента заполнения импульсной последовательности. Затем определяют параметры межсимвольной интерференции. Для этого вычисляют размах значений c1 функции y' для моментов времени, соответствующих передним фронтам входного сигнала, затем значение с2 функции y' для моментов времени, соответствующих задним фронтам входного сигнала. Среднее значение величин c1 и c2 соответствует значению межсимвольной интерференции. В блоке 407 устраняют компоненты джиттера, зависящего от данных, из первой функции у ошибок временных интервалов. Данная операция происходит путем вычитания функции y' усредненной ошибки временных интервалов из первой функции у ошибок временных интервалов. В результате получают вторую функцию z ошибок временных интервалов. Функция y' усредненной ошибки временных интервалов дает оценку зависимой от данных функции ошибок временных интервалов, таким образом, после ее вычитания из функции у останется только независимая от данных составляющая функции ошибок временных интервалов. В блоке 408 происходит заполнение неизвестных значений функции z, вызванных повторением логических символов во входном сигнале х. Последовательность операций, выполняемых в блоке 408, представлена в виде блок-схемы на фиг.5.

Вторая функция z ошибок временных интервалов из блока 407 поступает в блок 501, где неизвестные значения функции z заменяют нулями. В результате этой операции получают третью функцию g ошибок временных интервалов. Далее в блоке 502 выполняют прямое ДПФ функции g. Результатом данной операции является спектр G третьей функции ошибок временных интервалов. Вычисление спектра G в блоке 502 может быть реализовано посредством быстрого преобразования Фурье. Перед выполнением процедуры прямого преобразования Фурье для устранения эффекта «растекания спектра» третья функция g ошибок временных интервалов может быть умножена на оконную функцию, например на окно Блэкмана [Марпл-мл. С.Л. Цифровой спектральный анализ и его приложения. / Пер. с англ. М.: Мир, 1990, 584 с.]. На следующем шаге в блоке 503 формируют усредненный спектр G' третьей функции ошибок временных интервалов путем усреднения амплитуд |G| спектральных составляющих спектров G третьих функций ошибок временных интервалов соседних спектральных векторов. Усреднение амплитуд может быть вычислено как взвешенное среднее установленного числа измерений или как скользящее среднее с экспоненциальными, линейными или другими весами. В блоке 504 определяют пики усредненного спектра G' третьей функции ошибок временных интервалов, которые по амплитуде превышают уровень шумов. Частоты усредненного спектра G', соответствующие пиковым значениям, заносят в массив F_P2. Один из способов нахождения пиковых значений может состоять в нахождении порога Т2 путем нахождения среднего значения спектра G' по всем частотам и умножении полученного среднего значения на постоянный коэффициент. Значения усредненного спектра G' третьей функции ошибок временных интервалов, которые превышают порог Т2, относят к спектральным пикам и их частоты записывают в массив F_P2. В блоке 505 обнуляют амплитуды |G| спектральных составляющих спектра G третьей функции ошибок временных интервалов на частотах, которые не вошли в массив F_P2, то есть на частотах, которые на соответствуют пиковым значениям спектра. В результате данной операции формируют модифицированный спектр S третьей функции ошибок временных интервалов. В блоке 506 модифицированный спектр S третьей функции ошибок временных интервалов из частотной области переводят во временную в результате выполнения обратного ДПФ. На выходе блока 506 формируют модифицированную функцию s третьей функции ошибок временных интервалов. Если в блоке 502 перед выполнением прямого ДПФ третья функция g ошибок временных интервалов была умножена на оконную функцию, например на окно Блэкмана, то после обратного ДПФ необходимо устранить влияние окна на полученную модифицированную функцию s путем умножения ее на обратную оконную функцию.

Далее в блоке 507 вычисляют коэффициент k усиления модифицированной функции s третьей функции ошибок временных интервалов путем подсчета количества N_Δ изменений состояния (знакоперемен) входного сигнала x и деления длины сигнального вектора N на количество знакоперемен N_Δ. В блоке 508 выполняют усиление модифицированной функции s третьей функции ошибок временных интервалов в k раз. Далее в блоке 509 заполняют неизвестные значения второй функции z ошибок временных интервалов путем подстановки значений из усиленной в k раз модифицированной функции s третьей функции ошибок временных интервалов из соответствующих временных интервалов. В результате заполнения неизвестных значений на выходе блока 509 формируют функцию w ошибок временных интервалов, у которой все значения известны. Значения функции w ошибок временных интервалов, которые были подставлены из модифицированной функции s третьей функции ошибок временных интервалов, обозначают как «интерполированные» и после разделения случайного и периодического джиттера спектральным методом не учитывают при построении гистограмм периодического и случайного джиттера. Выход блока 509 является общим выходом блока 408.

Сформированная в блоке 408 функция w ошибок временных интервалов поступает на вход блока 409, где выполняют прямое ДПФ, в результате которого формируют спектр W функции ошибок временных интервалов. Перед выполнением процедуры прямого ДПФ для устранения эффекта «растекания спектра» функция w ошибок временных интервалов может быть умножена на оконную функцию, например на окно Блэкмана. На следующем шаге в блоке 410 формируют усредненный спектр W' функции ошибок временных интервалов путем усреднения амплитуд |W| спектральных составляющих спектров W функций ошибок временных интервалов соседних спектральных векторов. Усреднение амплитуд может быть вычислено как взвешенное среднее установленного числа измерений или как скользящее среднее с экспоненциальными, линейными или другими весами. В блоке 411 определяют пиковые значения усредненного спектра W' функции ошибок временных интервалов, которые по амплитуде превышают уровень шумов. Частоты усредненного спектра W', соответствующие пиковым значениям, заносят в массив F_P. Один из способов нахождения спектральных пиков описан выше.

Массив частот спектральных пиков F_p может отличаться от массива частот F_p2. Это связано с тем, что при заполнении неизвестных значений в функции z нулевыми значениями спектральный уровень шумов в спектре G' будет больше спектрального уровня шумов в спектре W', особенно при наличии одной или нескольких относительно мощных гармонических составляющих периодического джиттера. В результате этого некоторые гармонические составляющие периодического джиттера могут быть неразличимы на уровне шумов спектра G' и не попасть в массив F_P2, а при анализе спектра W', в котором спектральный уровень шумов соответствует истинному, гармонические составляющие с малой амплитудой могут быть различимы и внесены в массив F_p.

Блоки 412, 413, 414 и 415 описывают операции по анализу периодического джиттера. Сначала в блоке 412 вычисляют модифицированный спектр Р периодического джиттера. На частотах, вошедших в массив F_p, модифицированный спектр Р заполняют амплитудами из усредненного спектра W' и фазами из спектра W, а на частотах, не вошедших в F_p, амплитуды обнуляют. Затем в блоке 413 вычисляют обратное ДПФ от модифицированного спектра Р периодического джиттера. В результате этой операции формируют функцию p ошибок временных интервалов периодического джиттера. Если в блоке 409 перед выполнением прямого ДПФ функция w ошибок временных интервалов была умножена на оконную функцию, то после обратного ДПФ необходимо устранить влияние окна на полученную функцию p ошибок временных интервалов периодического джиттера путем умножения ее на обратную оконную функцию. Далее в блоке 414 вычисляют скользящую гистограмму значений функции р. Значения функции p, соответствующие неизвестным значениям функции z и помеченные как «интерполированные», не участвуют в построении гистограммы периодического джиттера. Далее в блоке 415 по гистограмме определяют размах значений периодического джиттера PJ_pp.

Блоки 416, 417, 418 и 419 описывают операции по анализу случайного джиттера. В блоке 416 вычисляют усредненную спектральную плотность мощности R' функции ошибок временных интервалов путем усреднения квадратов амплитуд спектра W функций ошибок временных интервалов. Усреднение квадратов амплитуд |W|² может быть вычислено как взвешенное среднее установленного числа измерений или как скользящее среднее с экспоненциальными, линейными или другими весами. Далее в блоке 417 формируют модифицированный спектр Q случайного джиттера, который состоит из амплитуд и фаз спектра W на частотах, не вошедших в массив F_p, и амплитуд, равных корню квадратному из разности усредненной спектральной плотности мощности R' и квадрата модуля усредненного спектра W', и случайных, равномерно распределенных фаз на частотах F_p. После этого в блоке 418 выполняют обратное ДПФ от модифицированного спектра Q случайного джиттера. В результате данной операции формируют функцию q ошибок временных интервалов случайного джиттера. Если в блоке 409 перед выполнением прямого ДПФ функция w ошибок временных интервалов была умножена на оконную функцию, то после обратного ДПФ необходимо устранить влияние окна на полученную функцию q ошибок временных интервалов случайного джиттера путем умножения ее на обратную оконную функцию. Далее в блоке 419 из функции q ошибок временных интервалов случайного джиттера устраняют значения, соответствующие неизвестным значениям функции z и помеченные как «интерполированные».

Следующим шагом является расчет скользящего среднеквадратического отклонения RJ_rms случайного джиттера по формуле:

где L - количество знакоперемен в сигнальных векторах, используемых при вычислении скользящего среднеквадратического значения;

- среднее значение функций q сигнальных векторов, используемых при вычислении RJ_rms.

При вычислении среднеквадратического отклонения RJ_rms и среднего значения суммирование производят только по известным, не помеченным как «интерполированные», значениям функций q ошибок временных интервалов случайного джиттера сигнальных векторов.

При вычислении скользящего среднеквадратического отклонения RJ_rms случайного джиттера могут быть использованы линейные, экспоненциальные или другие веса для взвешивания значений функций q сигнальных векторов, используемых в расчетах.

В блоке 420 принимают решение о необходимости выполнения дальнейшего усреднения результатов. При решении выполнения дальнейшего измерения и усреднении полученных результатов производят переход к блоку 402 и обработку нового сигнального вектора сигнала данных. В противном случае процесс обработки сигнала данных прекращают. Процесс усреднения полученных результатов обеспечивает более высокую точность измерений по сравнению с методом, использующим один сигнальный вектор входного сигнала.

Для проверки работоспособности предлагаемого способа разделения джиттера сигнала данных было произведено математическое моделирование по оцениванию параметров периодического и случайного джиттера. В качестве случайной составляющей был принят случайный гауссовский процесс n(i) с нулевым математическим ожиданием и среднеквадратическим отклонением σ=2. В качестве периодических составляющих были взяты три гармонических сигнала с относительными частотами ƒ₁=0.25, ƒ₂=0.345, ƒ₃=0.44, амплитудами A₁=0.79, А₂=0.835, A₃=0.51 и случайными фазами φ₁, φ₂ и φ₃. Длина выборки (сигнального вектора) была принята за N=2¹⁴. Спектр последовательности

i=0…N-1, представлен на фиг.1. Из данной последовательности случайным образом (с вероятностью 0,5) были удалены значения, тем самым была смоделирована вторая функция z ошибок временных интервалов от случайного входного сигнала данных.

Далее был применен спектральный метод оценки параметров периодического

PJ _рр и случайного RJ_rms джиттера согласно прототипу и предлагаемому способу. Амплитудные спектры восстановленных последовательностей ошибок временных интервалов представлены на фиг.2 и 3 соответственно, а результаты моделирования представлены в таблице на фиг.6.

В качестве критерия, по которому была оценена точность разделения компонентов общего джиттера согласно прототипу и предлагаемому способу, была выбрана средняя абсолютная ошибка, вычисляемая по формуле:

где n - количество проведенных опытов;

- значение исходного значения оцениваемого параметра в i-м опыте;

у_i - значение оцениваемого параметра в i-м опыте.

Как видно из таблицы на фиг.6, предлагаемый способ обеспечивает более высокую точность оценивания компонентов общего джиттера сигнала данных по сравнению с прототипом по выбранному критерию. Необходимо отметить, что при увеличении мощности периодической составляющей общего джиттера по сравнению со случайной точность оценки параметров RJ_rms и PJ_рр по прототипу резко падает, что не наблюдается в предлагаемом способе.

Способ разделения джиттера случайного сигнала данных, заключающийся в том, что получают и сохраняют входной сигнал в виде сигнальных векторов, формируют функцию исходной структуры данных первого сигнального вектора для каждого последующего сигнального вектора, следующего за первым сигнальным вектором, вычисляют функцию структуры данных, производят временной сдвиг функции структуры данных для выравнивания по оси времени с функцией исходной структуры данных первого сигнального вектора, вычисляют первую функцию ошибок временных интервалов, вычисляют функцию усредненной ошибки временных интервалов как скользящее среднее первых функций ошибок временных интервалов, определяют параметры джиттера, зависящего от данных, вычисляют вторую функцию ошибок временных интервалов путем вычитания функции усредненной ошибки временных интервалов из первой функции ошибок временных интервалов, выполняют прямое дискретное преобразование Фурье для перевода функции ошибок временных интервалов в частотную область, вычисляют усредненный спектр ошибок временных интервалов путем усреднения амплитуд спектральных составляющих спектров функции ошибок временных интервалов соседних сигнальных векторов, формируют массив частот F_p, соответствующий частотам пиковых значений амплитуд в усредненном спектре ошибок временных интервалов, вычисляют модифицированный спектр периодического джиттера на частотах F_p с амплитудами усредненного спектра ошибок временных интервалов и фазами спектра ошибок временных интервалов, вычисляют временную последовательность периодического джиттера путем обратного преобразования Фурье от модифицированного спектра периодического джиттера, вычисляют гистограмму временной последовательности периодического джиттера, определяют размах значений периодического джиттера по гистограмме, вычисляют усредненную спектральную плотность мощности функции ошибок временных интервалов путем усреднения квадратов амплитуд спектральных составляющих спектров функции ошибок временных интервалов соседних сигнальных векторов, вычисляют модифицированный спектр случайного джиттера путем подстановки на частотах F_p амплитуды, равной корню квадратному из разности усредненной спектральной плотности мощности и квадрата модуля усредненного спектра ошибок временных интервалов, и случайной равномерно распределенной фазы, выполняют обратное преобразование Фурье от модифицированного спектра случайного джиттера, вычисляют среднеквадратическое отклонение значений случайного джиттера, принимают решение о дальнейшем усреднении результатов, отличающийся тем, что после вычисления второй функции ошибок временных интервалов вычисляют третью функцию ошибок временных интервалов путем подстановки нулевых значений во вторую функцию ошибок временных интервалов в интервалах, не имеющих переходов состояний входного сигнала, выполняют прямое дискретное преобразование Фурье от третьей функции ошибок временных интервалов, вычисляют усредненный спектр третьей функции ошибок временных интервалов путем усреднения амплитуд спектральных составляющих спектров третьих функций ошибок временных интервалов соседних сигнальных векторов, формируют массив частот F_p2, соответствующий частотам амплитудных пиков в усредненном спектре третьей функции ошибок временных интервалов, формируют модифицированный спектр третьей функции ошибок временных интервалов путем обнуления амплитуд на частотах, не вошедших в массив F_p2, выполняют обратное дискретное преобразование Фурье от модифицированного спектра третьей функции ошибок временных интервалов, подсчитывают количество изменений состояния входного сигнала в сигнальном векторе, вычисляют коэффициент усиления модифицированной третьей функции ошибок временных интервалов путем деления длины сигнального вектора на количество изменений состояния входного сигнала в сигнальном векторе, усиливают модифицированную третью функцию ошибок временных интервалов, формируют функцию ошибок временных интервалов путем подстановки в интервалы второй функции ошибок временных интервалов, не имеющих переходов состояний входного сигнала, значений из соответствующих интервалов модифицированной третьей функции ошибок временных интервалов, а затем выполняют прямое дискретное преобразование Фурье для перевода функции ошибок временных интервалов в частотную область.