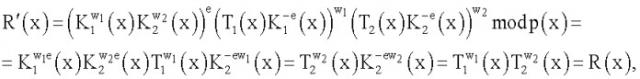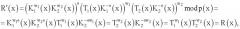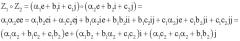Способ формирования и проверки подлинности электронной цифровой подписи, заверяющей электронный документ

Способ формирования и проверки подлинности электронной цифровой подписи, заверяющей электронный документ

Иллюстрации

Показать все

Реферат

Изобретение относится к области электросвязи и вычислительной техники, а конкретнее к области криптографических способов аутентификации электронных сообщений, передаваемых по телекоммуникационным сетям и сетям ЭВМ, и может быть использовано в системах передачи электронных сообщений (документов), заверенных электронной цифровой подписью (ЭЦП), представленной в виде битовой строки (БС) или нескольких БС. Здесь и далее под БС понимается электромагнитный сигнал в двоичной цифровой форме, параметрами которого являются: число битов и порядок следования их единичных и нулевых значений (толкование используемых в описании терминов приведены в конце описания).

Известен способ формирования и проверки ЭЦП, предложенный в патенте США №4405829 от 20.09.1983 и детально описанный также и в книгах [1. М.А.Иванов. Криптография. М., КУДИЦ-ОБРАЗ, 2001; 2. А.Г.Ростовцев, Е.Б.Маховенко. Введение в криптографию с открытым ключом. С.-Петербург, Мир и семья, 2001. - с.43]. Известный способ заключается в следующей последовательности действий:

формируют секретный ключ в виде трех простых многоразрядных двоичных чисел (МДЧ) p, q и d, представленных тремя БС;

формируют открытый ключ (n, е) в виде пары МДЧ n и e, где n - число, представляющее собой произведение двух простых МДЧ p и q, и e - МДЧ, удовлетворяющее условию

принимают электронный документ (ЭД), представленный БС H, в зависимости от значения H, под которым понимается значение МДЧ, представленное БС H, и значения секретного ключа формируют ЭЦП в виде МДЧ

формируют первое проверочное МДЧ A=H;

формируют второе проверочное МДЧ B, для чего МДЧ S возводят в целочисленную степень e по модулю n:

сравнивают сформированные проверочные МДЧ A и B;

при совпадении параметров сравниваемых МДЧ А и В делают вывод о подлинности ЭЦП.

Недостатком известного способа является относительно большой размер подписи и необходимость увеличения размера подписи при разработке новых более эффективных методов разложения числа n на множители или при росте производительности современных вычислительных устройств. Это объясняется тем, что значение элемента подписи S вычисляются путем выполнения арифметических операций по модулю n, а стойкость ЭЦП определяется сложностью разложения модуля n на множители p и q.

Известен также способ формирования и проверки подлинности ЭЦП Эль-Гамаля, описанный в книге [Молдовян А.А., Молдовян Н.А., Советов Б.Я. Криптография. - СПб, Лань., 2000. - с.156-159], который включает следующие действия:

формируют простое МДЧ p и двоичное число G, являющееся первообразным корнем по модулю p, генерируют секретный ключ в виде МДЧ x, в зависимости от секретного ключа формируют открытый ключ в виде МДЧ принимают ЭД, представленный в виде МДЧ Н, в зависимости от Н и секретного ключа формируют ЭЦП Q в виде двух МДЧ S и R, то есть

осуществляют процедуру проверки подлинности ЭЦП, включающую вычисление двух контрольных параметров с использованием исходных МДЧ p, G, Y, Н и S путем возведения МДЧ G, Y, R в дискретную степень по модулю p и сравнение вычисленных контрольных параметров;

при совпадении значений контрольных параметров делают вывод о подлинности ЭЦП.

Недостатком данного способа также является относительно большой размер ЭЦП. Это объясняется тем, что значения элементов подписи S и R вычисляют путем выполнения арифметических операций по модулю p - 1 и по модулю p, соответственно.

Известен также способ формирования и проверки ЭЦП, предложенный в патенте США №4995089 от 19.02.1991. Известный способ заключается в следующей последовательности действий:

формируют простое МДЧ p, такое, что где q - простое МДЧ;

формируют простое МДЧ а, такое, что и

методом генерации случайной равновероятной последовательности формируют секретный ключ в виде МДЧ k;

формируют открытый ключ в виде МДЧ y по формуле

принимают ЭД, представленный МДЧ M;

формируют ЭЦП в виде пары МДЧ (e, s), для чего генерируют случайное МДЧ t, формируют МДЧ R по формуле формируют МДЧ где знак обозначает операцию присоединения двух МДЧ и f - некоторая специфицированная хэш-функция, значение которой имеет фиксированную длину (обычно 160 или 256 бит), независимую от размера аргумента, т.е. от размера МДЧ а затем формируют МДЧ s по формуле

формируют первое проверочное МДЧ А, для чего генерируют МДЧ по формуле и формируют МДЧ

формируют второе проверочное МДЧ В путем копирования МДЧ е:

сравнивают сформированные проверочные МДЧ А и В;

при совпадении параметров сравниваемых МДЧ А и В делают вывод о подлинности ЭЦП.

Недостатком способа по патенту США является относительно высокая вычислительная сложность процедуры формирования и проверки ЭЦП, что связано с тем, что для обеспечения минимально требуемого уровня стойкости требуется использовать простой модуль p разрядностью не менее 1024 бит.

Наиболее близким по своей технической сущности к заявленному является известный способ формирования и проверки подлинности ЭЦП, предлагаемый российским стандартом ГОСТ Р 34.10-2001 и описанный, например, в книге [Б.Я.Рябко, А.Н.Фионов. Криптографические методы защиты информации. М., Горячая линия - Телеком, 2005. - 229 с. (см. с.110-111)], согласно которому ЭЦП формируется в виде пары МДЧ r и s, для чего генерируют эллиптическую кривую (ЭК) в виде совокупности точек, причем каждая точка представляется двумя координатами в декартовой системе координат в виде двух МДЧ, называемых абсциссой (x) и ординатой (y), затем осуществляют операции генерации точек ЭК, сложения точек ЭК и умножения точки ЭК на число, а также арифметические операции над МДЧ, после чего в результате выполненных операций формируются МДЧ r и s. Указанные операции над точками выполняются как операции над МДЧ, являющимися координатами точек, по известным формулам [Б.Я.Рябко, А.Н.Фионов. Криптографические методы защиты информации. М., Горячая линия - Телеком, 2005. - 229 с. (см. с.110-111)]. Операция сложения двух точек А и В с координатами и соответственно, выполняется по формулам:

и

где если точки А и В не равны, и если точки A и В равны. При вычислении значения k выполняется операция деления МДЧ по модулю простого МДЧ, что ограничивает производительность формирования и проверки подлинности ЭЦП по стандарту ГОСТ Р 34.10-2001. Операция умножения точки А на натуральное число n определяется как многократное сложение токи А:

(n раз)

Результатом умножения любой точки ЭК на нуль определяется точка, называемая бесконечно удаленной точкой и обозначаемой буквой Ο. Две точки и называются противоположными. Умножение на целое отрицательное число -n определяется следующим образом: По определению принимают, что сумма двух противоположных точек равна бесконечно удаленной точке Ο.

В прототипе, т.е. в способе формирования и проверки подлинности ЭЦП по стандарту ГОСТ Р 34.10-2001, генерируют ЭК, описываемую уравнением поэтому генерация ЭК состоит в генерации чисел a, b и p, являющихся параметрами ЭК и однозначно задающих множество точек ЭК, абсцисса и ордината каждой из которых удовлетворяет указанному уравнению. Ближайший аналог (прототип) заключается в выполнении следующей последовательности действий:

генерируют эллиптическую кривую (ЭК), которая представляет собой совокупность пар МДЧ, называемых точками ЭК и обладающих определенными свойствами (см. Приложение 1, пп.27-31);

методом генерации случайной равновероятной последовательности формируют секретный ключ в виде МДЧ k;

формируют открытый ключ Р в виде двух МДЧ, являющихся координатами точки ЭК Р, для чего генерируют точку G, имеющую значение порядка, равное q (порядком точки ЭК называется наименьшее положительное целое число q, такое, что результатом умножения данной точки на число q является так называемая бесконечно удаленная точка О; результатом умножения любой точки ЭК на нуль по определению является точка О [Б.Я.Рябко, А.Н.Фионов. Криптографические методы защиты информации. М., Горячая линия - Телеком, 2005. - 229 с. (см. с.97-130)]; см. также Приложение 1, пп.27-31) и генерируют открытый ключ путем умножения точки G на МДЧ k, т.е. формируют открытый ключ по формуле

принимают ЭД, представленный МДЧ Н;

генерируют случайное МДЧ 0<t<q, по которому формируют точку R по формуле R=tG;

формируют ЭЦП Q в виде пары МДЧ (r,s) для чего генерируют МДЧ r по формуле где - абсцисса точки R, а затем генерируют МДЧ s по формуле

формируют первое проверочное МДЧ А, для чего генерируют МДЧ v по формуле и МДЧ w по формуле затем генерируют точку по формуле после чего МДЧ А получают по формуле где - абсцисса точки

формируют второе проверочное МДЧ В путем копирования МДЧ r:

сравнивают сформированные проверочные МДЧ А и В;

при совпадении параметров сравниваемых МДЧ А и В делают вывод о подлинности ЭЦП.

Недостатком ближайшего аналога является относительно невысокая производительность процедуры формирования и проверки ЭЦП, что связано с тем, что выполнение операций над точками ЭК включает операцию деления МДЧ по модулю простого МДЧ, которая требует времени выполнения, длительность которого более чем в 10 раз превышает время выполнения операции умножения.

Целью изобретения является разработка способа формирования и проверки подлинности ЭЦП, заверяющей ЭД, свободного от операции деления по модулю простого МДЧ, благодаря чему повышается производительность процедур формирования и проверки ЭЦП.

Поставленная цель достигается тем, что в известном способе формирования и проверки подлинности ЭЦП, заверяющей ЭД, заключающемся в том, формируют секретный ключ, по секретному ключу формируют открытый ключ в виде, по крайней мере, одной БС, принимают ЭД, представленный, по крайней мере, одной БС Н, в зависимости от принятого ЭД и значения секретного ключа формируют ЭЦП в виде, по крайней мере, двух БС, формируют первую А и вторую В проверочные БС, сравнивают их и при совпадении их параметров делают вывод о подлинности ЭЦП, новым в заявленном изобретении является то, что формируют секретный ключ в виде, по крайней мере, двух элементов, каждый из которых представляет собой, по крайней мере, одну БС, и при формировании открытого ключа осуществляют операции возведения первого и второго элементов секретного ключа в степени -разрядного двоичного числа w₁ z₁-разрядного двоичного числа w₂ соответственно, где и

Благодаря тому, что в заявленном способе формирования и проверки подлинности ЭЦП не выполняется операция деления по модулю и стойкость ЭЦП обеспечивается при сравнительно малых размерах модуля p и степеней w₁ и w₂, снижается сложность операций возведения в степень, за счет чего повышается производительность процедуры формирования и проверки ЭЦП.

Новым является также и то, что формируют секретный ключ в виде двух МДЧ K₁ и K₂, по секретному ключу формируют открытый ключ в виде МДЧ Y путем возведения МДЧ K₁ в степень w₁ по модулю простого МДЧ p, возведения МДЧ K₂ в степень w₂ по модулю p и перемножения значений и по формуле причем где N- четное натуральное число, w, w¹ и - простые МДЧ, а и

Новым является также и то, что ЭЦП формируют в виде трех МДЧ e, S₁ и S₂ путем генерации двух случайных МДЧ Т₁ и T₂, генерации МДЧ R по формуле генерации первого МДЧ е ЭЦП по формуле где - выражение, задающее правило вычисления МДЧ е, генерации второго и третьего МДЧ S₁ и S₂ ЭЦП по формулам и а первую А и вторую B проверочные БС формируют в виде МДЧ по формулам где и

Реализация заявленного способа формирования и проверки подлинности ЭЦП на основе выполнения операций над МДЧ обеспечивает удобство его программной реализации.

Новым является также и то, что формируют секретный ключ в виде двух многочленов и где x - формальная переменная, по секретному ключу формируют открытый ключ в виде многочлена Y(x) путем возведения многочлена в степень w₁ по модулю неприводимого многочлена p(x), возведения многочлена в степень w₂ по модулю неприводимого многочлена p(x) и перемножения значений и по формуле где w₁ и w₂ - простые МДЧ.

Новым является также и то, что ЭЦП формируют в виде МДЧ е и двух многочленов и путем генерации двух случайных многочленов и генерации многочлена R(x) по формуле генерации МДЧ е ЭЦП по формуле где - выражение, задающее правило вычисления МДЧ е, генерации первого и второго многочленов и ЭЦП по формулам и а первую А и вторую В проверочные БС формируют в виде МДЧ по формулам где и

Реализация заявленного способа формирования и проверки подлинности ЭЦП на основе выполнения операций над многочленами по модулю неприводимого многочлена, в случае задания многочленов над конечным полем достаточно большой характеристики, обеспечивает увеличение производительности программной реализации. В случае задания многочленов над конечным полем достаточно малой характеристики, например характеристики 2, обеспечивается увеличение производительности аппаратной реализации при одновременном снижении сложности схемотехнической реализации. При аппаратной реализации заявленного способа наибольший выигрыш в производительности обеспечивается при использовании двоичных многочленов, т.е. многочленов над простым полем характеристики 2.

Новым является также и то, что формируют секретный ключ в виде двух векторов БС K₁ и K₂, по секретному ключу формируют открытый ключ в виде вектора БС Y путем возведения вектора БС K₁ в степень w₁, возведения вектора БС K₂ в степень w₂ и перемножения значений и по формуле где знак обозначает операцию умножения векторов БС, и принимают ЭД, представленный двумя битовыми строками и .

Новым является также и то, что ЭЦП формируют в виде МДЧ е и двух векторов БС S₁ и S₂ путем генерации двух случайных векторов БС T₁ и T₂ а, генерации вектора БС R по формуле генерации МДЧ е ЭЦП по формуле где - выражение, задающее правило вычисления МДЧ е, генерации первого и второго векторов БС S₁ и S₂ ЭЦП по формулам и а первую А и вторую В проверочные БС формируют в виде МДЧ по формулам где и

Реализация заявленного способа формирования и проверки подлинности ЭЦП на основе выполнения операций над векторами БС обеспечивает возможность эффективного распараллеливания операции умножения в конечной группе, на основе которой реализуется заявленный способ формирования и проверки ЭЦП, заверяющей ЭД, благодаря чему обеспечивается дальнейшее повышении скорости формирования и проверки ЭЦП при аппаратной реализации.

Конкретные варианты заявленного способа формирования и проверки ЭЦП, заверяющей ЭД, реализуются путем выполнения действий по п.1 формулы изобретения над элементами конечных групп с коммутативной групповой операцией. Наиболее важными для практического применения являются варианты использования следующих трех типов конечных групп:

1) конечные группы МДЧ, включающие набор МДЧ {1, 2, 3,…,р-1}, где р - простое МДЧ, причем групповой операцией является умножение МДЧ по модулю р; данный тип групп широко применяется при реализации известных способов формирования и проверки ЭЦП [Смарт Н. Мир программирования. Криптография.- М., ТЕХНОСФЕРА, 2005. - 525 с.];

2) конечные группы многочленов, в которых групповой операцией является умножение многочленов по модулю неприводимого многочлена; конечные группы многочленов также широко представлены в хорошо известных литературных источниках и применяются в криптографических алгоритмах [Венбо Мао. Современная криптография. Теория и практика. - М., СПб., Киев. Издательский дом «Вильямс», 2005. - 763 с.].

3) конечные группы векторов БС, в которых групповой операцией является умножение векторов БС; данный тип групп является менее известным и при построении способов формирования и проверки подлинности ЭЦП ранее не применялся; достаточно детальное рассмотрение криптографических применений групп векторов БС дано в работе [Молдовян Н.А. Группы векторов для алгоритмов электронной цифровой подписи // Вестник СПбГУ. Сер. 10. 2008];

ниже в рамках рассмотрения примера 3 детально рассматриваются построение конечных групп векторов БС и способы задания операции умножения векторов БС, являющейся групповой операцией.

Группа - это множество математических элементов некоторой природы, над элементами которого задана некоторая операция таким образом, что оно образует алгебраическую структуру, обладающую следующим набором свойств: операция ассоциативна, результатом выполнения операции над двумя элементами является элемент этой же структуры, существует нейтральный элемент такой, что при выполнении операции над ним и другим некоторым элементом а группы результатом является элемент а. Детальное описание групп дано в широко доступной математической литературе, например в книгах [А.Г.Курош. Теория групп. - М., изд-во «Наука», 1967, 648 с.] и [М.И. Каргаполов, Ю.И. Мерзляков. Основы теории групп. - М., изд-во «Наука. Физматлит», 1996, 287 с.]. Операция, определенная над элементами группы, называется групповой операцией. Группа называется циклической, если каждый ее элемент может быть представлен в виде для некоторого натурального числа n, где a - элемент данной подгруппы, называющийся генератором или образующим элементом циклической подгруппы, и степень n означает, что над элементом а выполняются n последовательных операций, т.е. (n раз). Если группа содержит конечное число элементов, то она называется конечной группой. Число элементов в группе называется порядком группы. Известно, что если порядок группы есть простое число, то она циклическая [А.И.Кострикин. Введение в алгебру. Основы алгебры. М.: Физматлит, 1994. - 320 с.]. Для элементов группы также применяется понятие порядка. Порядком элемента группы является минимальное значение степени, в которую нужно возвести этот элемент, чтобы результатом операции было получение нейтрального элемента группы.

Обычно при разработке способов формирования и проверки ЭЦП используются циклические группы большого простого порядка или группы, порядок которых делится нацело на большое простое число [Венбо Мао. Современная криптография. Теория и практика. - М., СПб., Киев. Издательский дом «Вильямс», 2005. - 763 с.]. При этом стойкость способов формирования и проверки ЭЦП определяется сложностью задачи дискретного логарифмирования, которая состоит в определении значения степени n, в которую надо возвести заданный элемент группы, чтобы результатом этой операции был некоторый другой заданный элемент группы [Молдовян Н.А. Практикум по криптосистемам с открытым ключом. - СПб.: БХВ-Петербург, 2007. - 298 с.].

Стойкость ЭЦП, генерируемой по заявленному способу формирования и проверки ЭЦП, заверяющей ЭД, основана на том факте, что операция извлечения корней степени, равной простому МДЧ w, из элементов конечной группы порядка Ω в случае, когда МДЧ w делит МДЧ Ω, может быть выполнена только для числа элементов групп, равного При достаточно большом значении w вероятность того, что случайно сгенерированный элемент группы а может быть представлен в виде является пренебрежимо малой. Кроме того, для обеспечения стойкости следует выбрать соответствующими значения МДЧ w₁ и w₂. Последнее можно сделать различными способами. Например, можно задать МДЧ w₁ в виде a МДЧ w₂ в виде где w, и - простые 80-разрядные числа. Рассмотрим на примере частного варианта реализации заявленного способа формирования и проверки ЭЦП, соответствующего п.3 формулы изобретения, возможные атаки на ЭЦП. Без знания секретного ключа подделка ЭЦП может быть осуществлена выбором значений T₁ и T₂, генерации МДЧ вычисления МДЧ где H - МДЧ, представляющее ЭД, с последующим вычислением пары МДЧ S₁ и S₂. Однако шаг вычисления МДЧ S₁ и S₂ требует решения уравнения вида

где неизвестными являются S₁ и S₂. При этом правая часть уравнения имеет случайное значение, если в качестве функции выбрать некоторую хэш-функцию или функцию вида где

Если задать значение одной из неизвестных, например S₂, то уравнение преобразуется в уравнение с одной неизвестной S₁ вида а затем к уравнению вида В последнем уравнении правая часть с пренебрежимо малой вероятностью будет иметь значение, при котором последнее уравнение разрешимо. Для проверки условия разрешимости выполняется одна операция возведения в степень по модулю р. Для получения случая, когда условие разрешимости удовлетворяется, требуется выполнить описанную попытку в среднем раз. При размере равном 80 бит и более, вычислительная сложность подделки ЭЦП настолько велика, что практически невыполнима. Аналогичным путем подделку подписи можно свести к решению уравнения относительно неизвестной S₂, когда требуется выполнить описанных попыток. При размере равном 80 бит и более, такой объем попыток вычислительно нереализуем. Попытка подделать подпись путем генерации МДЧ и вычисления МДЧ связана с вычислением МДЧ и таких, что выполняется соотношение Последнее соотношение выполняется, если выполняется соотношение которое сводится к диофантовому уравнению относительно неизвестных и вида Поскольку и где w, и - простые МДЧ, то указанное диофантовое уравнение имеет решение в целых числах только в случае, когда правая часть уравнения делится на МДЧ w, которое равно наибольшему общему делителю коэффициентов при неизвестных и (условия разрешимости диофантовых уравнений хорошо известны, см., например, книгу [Бухштаб А.А. Теория чисел. - М.: Просвещение, 1966. -384 с.]). Значение МДЧ е формируется по формуле и вероятность того, что диофантовое уравнение будет иметь решения, равна . При размере w, равном 80 бит, для получения одного случая разрешимости диофантового уравнения в среднем требуется выполнить 2⁸⁰ попыток подделки подписи, что превышает значение сложности, равное 2⁸⁰ операций возведения в степень по модулю p, т.е. второй тип атаки на ЭЦП, формируемую по заявленному способу, также практически невыполним. Рассмотрим примеры реализации заявленного способа формирования и проверки ЭЦП при использовании трех типов конечных групп, указанных выше.

Пример 1.

Данный пример иллюстрирует конкретный вариант реализации заявленного способа формирования и проверки ЭЦП по п.3 формулы изобретения. Пункт 3 раскрывает конкретный вариант реализации п.2, а последний пункт относится к частной реализации п.1, поэтому пример 1 иллюстрирует реализацию пп.1, 2 и 3 формулы изобретения. В данном примере вначале представлена обобщенная реализация способа по п.3 с использованием МДЧ произвольного размера, а затем приводится пример выполнения действий по п.3 с указанием конкретных численных значений, которые принимают используемые параметры. Доказательство корректности заявленного способа формирования и проверки подлинности ЭЦП при его реализации по п.3 дается в общем случае для произвольных значений МДЧ. В обобщенном виде выполняемые действия представляются следующей последовательностью действий.

1. Генерируют простое число p, такое, что p-1 содержит большие простые множители w, w' и w'' т.е. где N - четное число. В качестве МДЧ w₁ и w₂ используют числа и соответственно.

2. Генерируют секретный ключ в виде двух случайных МДЧ К₁ и К₂.

3. Формируют открытый ключ Y в виде МДЧ

3. Принимают ЭД, представленный МДЧ Н.

4. Формируют ЭЦП в виде трех МДЧ е, S₁ и S₂, для чего выполняют следующие действия:

4.1. Генерируют пару случайных МДЧ T₁ и T₂.

4.2. Вычисляют МДЧ

4.3. Вычисляют первое МДЧ е ЭЦП по формуле например,

4.4. Вычисляют второе МДЧ S₁ ЭЦП по формуле

4.5. Вычисляют третье МДЧ S₂ ЭЦП по формуле

5. Формируют первую проверочную БС А, для чего выполняют следующие действия.

5.1. Генерируют МДЧ

5.2. Формируют БС А в виде МДЧ, вычисляемого по формуле

т.е.

6. Формируют вторую проверочную БС В путем копирования МДЧ е:

7. Сравнивают первую и вторую проверочные БС А и В:

Если ЭЦП была сформирована корректно, то на шаге 7 приведенной последовательности действий будет получено совпадение проверочных БС. В этом случае делают вывод о подлинности ЭЦП, заверяющей ЭД. Корректность приведенного частного варианта реализации способа формирования и проверки подлинности ЭЦП доказывается следующим образом. Подставляя в формулу значения и получаем

т.е. получаемое в процессе проверки подлинной ЭЦП значение МДЧ равно МДЧ R, поэтому

Приведем пример частной реализации указанной выше последовательности действий для случая использования двухмерных векторов БС.

1. Генерируют простое число p, такое, что p-1 содержит большие простые множители w, w' и w'', т.е. где N - четное число:

р=207058210173317975283840168452786556059;

N=122; w=43391; w'=1037327; w''=37706592177541972343870177. w₁=ww'=45010655857;

w₂=ww''=1636126741175723721972870850207.

2. Генерируют секретный ключ в виде двух случайных МДЧ K₁ и К₂: К₁=716898509375431306272081;

К₂=84625032531337128506088.

3. Формируют открытый ключ Y в виде МДЧ, вычисляемого по формуле

=184786771613225274241947728803805332534;

=166715777768672168097282226515237158347;

Y=117996294309150575198921568244513363511.

3. Принимают ЭД, представленный МДЧ Н, в качестве которого может быть взято значение некоторой специфицированной хэш-функции от ЭД. Пусть получено МДЧ Н=938465839575624343596736.

4. Формируют ЭЦП в виде трех МДЧ е, S₁ и S₂, для чего выполняют следующие действия:

4.1. Генерируют пару случайных МДЧ Т₁ и T₂:

Т₁=36186064562670643172585697;

T₂=90758345139287902502537148;

4.2. Вычисляют МДЧ mod р:

=189875188145657029662935356717403411470;

=196150962023012787693205423497619024711;

R=152085758341426732402146934384987086068.

4.3. Вычисляют первое МДЧ е ЭЦП по формуле :е=17916429455.

4.4. Вычисляют второе МДЧ S₁ ЭЦП по формуле :

=81705713996940932088325229911270482200;

S₁=77096791017192058620671986273319937381.

4.5. Вычисляют третье МДЧ S₂ ЭЦП по формуле :

=178027052274072413960850519819518927832;

S₂=124719856404421356993673024300549206635.

5. Формируют первую проверочную БС А, для чего выполняют следующие действия.

5.1. Генерируют МДЧ :

=51112026969055849193858105601335008373;

=110039988699446955325815724938200899118;

=187553964633263335850348739028438656069;

=152085758341426732402146934384987086068.

5.2. Формируют БС А в виде МДЧ, вычисляемого по формуле :

A=17916429455.

6. Формируют вторую проверочную БС В путем копирования МДЧ е:

В=е=17916429455.

7. Сравнивают первую и вторую проверочные БС А и В: А=В. Поскольку параметры проверочных БС совпадают, делают вывод о подлинности ЭЦП, заверяющей ЭД.

Пример 2.

Данный пример иллюстрирует конкретный вариант реализации заявленного способа формирования и проверки ЭЦП по п.5 формулы изобретения. Пункт 5 раскрывает конкретный вариант реализации п.4, а последний пункт относится к частной реализации п.1, поэтому пример 2 иллюстрирует реализацию пп.1, 2 и 3 формулы изобретения. В данном примере вначале представлена обобщенная реализация способа по п.3 с использованием произвольных параметров многочленов, удовлетворяющих условиям, сформулированным в п.1, приводимой ниже последовательности действий. Доказательство корректности заявленного способа формирования и проверки подлинности ЭЦП при его реализации по п.5 дается в общем случае. Рассматриваемый в примере 2 частный вариант реализации заявленного способа связан с выполнением операций в конечной группе многочленов. В качестве та