Способ пеленгования с повышенной эффективностью

Способ пеленгования с повышенной эффективностью

Иллюстрации

Показать все

Реферат

Область техники

Изобретение относится к радиотехнике, в частности к радиопеленгации, и может быть использовано в системах определения направления на источники радиоизлучения, работающие на одной частоте.

Уровень техники

Многосигнальное пеленгование источников радиоизлучения (ИРИ) имеет место в процессе мониторинга радиоэлектронной обстановки при многолучевом распространении радиоволн, воздействии преднамеренных и непреднамеренных помех, отражениях сигнала от различных объектов и слоев атмосферы.

Известен способ определения двумерного пеленга [1], при котором достигается следующее.

1. Принимают многолучевой сигнал источника электромагнитного излучения

антенной решеткой из N+1 элементов и формируют ансамбль сигналов x_n (t), зависящих от времени t и номера антенного элемента n=0, …, N.

2. Синхронно преобразуют ансамбль принятых сигналов x_n (t) в цифровые сигналы

x_n(z), где z - номер временного отсчета сигнала.

3. Преобразуют цифровые сигналы x_n(z) в сигнал комплексного амплитудно-фазового распределения (АФР) описывающий амплитуды и фазы сигналов, принятых элементами решетки. Запоминают сигнал АФР

4. Генерируют и запоминают идеальный двумерный сигнал комплексной фазирующей функции размером N×М, зависящий от заданной частоты приема и описывающий возможные направления прихода сигнала от каждого потенциального источника, где М - число угловых положений, соответствующих заданным потенциально возможным направлениям прихода сигналов по азимуту α_m и углу места β_m, - номер направления.

5. Используя восстановленный вектор АФР и сигнал фазирующей функции синтезируют по известному алгоритму псевдообращения начальное приближение углового спектра сигнала которое запоминают для использования на очередной итерации.

6. Восстанавливают угловой спектр мощности углового спектра сигнала k≥1, полученного на предыдущей итерации.

7. Возводя смещенное на малую положительную величину полученное приближение углового спектра мощности в степень формируют зависящий от предыдущего решения двумерный взвешивающий сигнал размером M×M в форме диагональной матрицы

где p<1, - m-й элемент вектора ε - малое число.

8. Используя полученный взвешенный сигнал и запомненные сигналы и формируют взвешенный сигнал фазирующей функции сигнал весовых коэффициентов взвешивающий сигнал АФР вектор взвешенного АФР и зависящий от предыдущего решения текущий угловой спектр сигнала который запоминают для использования на очередной итерации.

9. Сравнивают энергию разности угловых спектров полученных на текущей и предыдущей итерации, с порогом δ. Значение порога выбирается, например, из условия

10. При невыполнении условия инициализируется очередная итерация синтеза углового спектра, на которой повторяются операции последовательного формирования сигналов запоминания и сравнения энергии разности угловых спектров с порогом δ.

11. При выполнении условия восстанавливают спектр мощности углового спектра сигнала полученного на текущей итерации синтеза, по максимумам которого определяют азимут α и угол места β каждого луча принятого многолучевого сигнала.

12. Полученные двумерные пеленги (α, β) выделенных лучей отображаются на картографическом фоне, чем обеспечивается повышение информативности пеленгования. Недостатки данного способа следующие.

- Угловой спектр получают по формуле

где p<1, что не гарантирует устойчивости решения к малым вариациям сигнала Поскольку сигнал получают на основе физических измерений, он неизбежно содержит в себе помеху. Таким образом, невозможно гарантировать устойчивое получение углового спектра

- Нет гарантии выполнения условия для угловых спектров за конечное число итераций.

- Результатом итерационного процесса является точечная оценка углового спектра которая не позволяет судить о ее надежности, так как имеет место помеха в сигнале АФР а также в сигнале фазирующей функции (несущая частота и геометрические параметры АС также содержат погрешности).

Указанные недостатки очевидно не позволят применять способ в реальных условиях из-за его недопустимо низкой практической эффективности (надежности, устойчивости и сходимости решения).

Раскрытие изобретения

Техническим результатом является повышение эффективности определения точечных оценок азимутальных и угломестных пеленгов источников радиоизлучения, а также повышение надежности результатов за счет получения интервальных оценок решения. Эффективность предлагаемого способа обеспечивается использованием аппарата многокритериального математического программирования, позволяющего учесть всевозможные виды дополнительных условий, которым должна удовлетворять оценка решения.

Способ пеленгования с повышенной эффективностью включает прием многолучевого сигнала многоэлементной антенной решеткой, синхронное преобразование ансамбля принятых сигналов, зависящих от времени и номера антенного элемента, в цифровые сигналы, преобразование цифровых сигналов в сигнал , описывающий распределение амплитуд и фаз на элементах решетки, формирование сигнала комплексной фазирующей функции, описывающего возможные направления прихода от каждого потенциального источника на заданной частоте приема.

Отличается тем, что получение углового спектра осуществляют введением переопределенного базиса посредством сетки пеленгов для формирования из исходной системы нелинейных уравнений системы линейных алгебраических уравнений (СЛАУ) и решением этой системы посредством формирования нескольких целевых функций и использованием, в зависимости от предъявляемых требований (критериев) эффективности, одного из методов многокритериального математического программирования, сведением многокритериальной задачи к однокритериальной задаче с ограничениями, получением итерационными вычислительными процедурами решения указанной однокритериальной задачи с ограничениями, определением по максимумам спектра мощности полученного углового спектра сигнала точечных сигналов азимута α и угла места β каждого луча принятого многолучевого сигнала.

Для дополнительного определения интервальных оценок указанных точечных сигналов на основе теоремы Крамера-Рао используют ковариационную матрицу решений, сформированную с помощью функции правдоподобия, связанной с указанной исходной системой нелинейных уравнений.

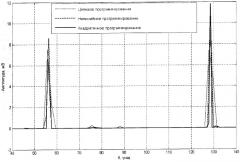
Результаты точечных и интервальных оценок пеленгов далее можно представлять в визуальном графическом виде для последующей работы людей с ними, представленном на чертеже, где

- показаны графики пеленгационной панорамы примера реализации способа с применением разных методов многокритериального математического программирования.

Осуществление изобретения

Необходимо определение следующих параметров ИРИ, присутствующих в эфире: количество; амплитуды (мощности) излучаемых сигналов; азимутальные пеленги и угломестные пеленги.

В качестве практически оправданного допущения для предлагаемого способа сигналы рассматривают как детерминированные, подверженные аддитивной помехе, оценки параметров которых подлежат определению.

Поскольку на результаты измерений неизбежно накладывается помеха, а также имеют место ошибки измерений, обусловленные используемой аппаратурой, дополнительно желательно получить не только точечные оценки искомых параметров, но и их ковариационные матрицы или, по крайней мере, дисперсии, для получения интервальных оценок.

Полагаем, что в эфире присутствует K ИРИ с азимутальными пеленгами угломестными пеленгами и амплитудами (мощностями) излучаемых сигналов сигнал комплексного АФР, описывающий амплитуды и фазы сигналов, принятых элементами АС, где N+1 - количество элементов АС. Используемый вид модуляции (амплитудная, частотная, фазовая и др.) не имеет принципиального значения.

В общем случае исходная система нелинейных уравнений относительно неизвестных α, β и имеет следующий вид:

где n(t) - вектор аддитивной помехи, имеющей нулевое математическое ожидание и ковариационную матрицу вида σ²I, I - единичная матрица, σ - среднеквадратическое отклонение (СКО); матрица (фазирующая функция) формируется с учетом вида сигналов, пеленгуемых ИРИ, и пространственной конфигурации АС.

Требуется определить для каждого из одновременно поступивших на АС сигналов амплитуду (мощность) s_k, азимутальный пеленг α_k и угломестный пеленг β_k.

Линеаризуем нелинейную модель (1) при помощи введения переопределенного базиса посредством сетки пеленгов. Будем считать, что задан интервал возможных значений азимутальных пеленгов (например, от 0° до 180°) и угломестных пеленгов (например, от 0° до 90°). Введем на данном интервале сетку пеленгов и сетку углов места системе (1) матрицу заменим матрицей

в которой неизвестными остаются только амплитуды, соответствующие азимутальным пеленгам и угломестным пеленгам .

Получаем СЛАУ относительно вектора неизвестных

Количество элементов вектора амплитуд сигналов (количество столбцов матрицы системы) увеличивается до произведения размерностей сеток азимутальных и угломестных пеленгов - M_α×M_β. Теперь вектор представляет собой распределение амплитуд (мощностей) по пеленгам (угловой спектр). В идеальном случае (шумы отсутствуют) количество ненулевых элементов вектора равно количеству фактически присутствующих в эфире ИРИ. Положение ненулевых элементов в векторе (в сетке пеленгов) характеризует пеленги соответствующих ИРИ.

Таким образом, введение сетки пеленгов решает не только проблему нелинейности задачи, но и проблему определения количества ИРИ.

Решив СЛАУ (3), получаем необходимую информацию по пеленгам.

Несмотря на линейность, задача (3) является вычислительно некорректном. Поэтому для ее решения необходимо применение специфических методов, в предлагаемом способе - это методы многокритериального математического программирования.

Предлагаемый способ пеленгования осуществляют следующим образом.

1. Принимают многолучевой сигнал источника электромагнитного излучения антенной решеткой из N+1 элементов и формируют ансамбль сигналов x_n(t), зависящих от времени t и номера антенного элемента n=0, …, N.

2. Синхронно преобразуют ансамбль принятых сигналов x_n(t) в цифровые сигналы

x_n(z), где z - номер временного отсчета сигнала.

3. Преобразуют цифровые сигналы - x_n(z) в сигнал комплексного амплитудно-фазового распределения (АФР) описывающий амплитуды и фазы сигналов, принятых элементами решетки. Запоминают сигнал АФР

4. Генерируют и запоминают идеальный двумерный сигнал комплексной фазирующей функции размером N×(M_α·M_β), зависящий от заданной частоты приема и описывающий возможные направления прихода сигнала от каждого потенциального источника, где М_α - число угловых положений, соответствующих заданным потенциально возможным направлениям прихода сигналов по азимуту и M_β - число угловых положений, соответствующих заданным потенциально возможным направлениям прихода сигналов по углу места

5. Формируют многокритериальную задачу математического программирования. Это преимущественно двухкритериальная задача:

с показателем степени нормы 0<р ≤ 1 и при ограничениях или ;

но может быть и трехкритериальная задача:

при ограничениях или .

6. Используя метод пороговой оптимизации или целевое программирование, от двухкритериальной задачи математического программирования переходят к однокритериальной задаче посредством перевода всех, кроме одного, из вышеуказанных функционалов в условия ограничений.

Метод пороговой оптимизации (или метод е-ограничений) приводит к различным возможным комбинациям целевых функций и ограничений:

a) при

b) при

c) при

d) при

Оценки правых частей ограничений δ и γ могут быть получены при независимой минимизации функционалов J₁, и J₂ при ограничениях или При этом может использоваться любой из методов математического программирования.

В целевом программировании существует две модели решения - архимедова и модель с приоритетами.

При использовании архимедовой модели все целевые функции переводят в ограничения и осуществляют минимизацию взвешенной суммы меры их отклонений от ограничений:

где w_i - весовые коэффициенты,

d_i - отклонения от ограничений.

В модели с приоритетами осуществляют последовательный перевод целевых функций в ограничения и минимизацию отклонения значений целевых функций от ограничений. При этом найденное на данном шаге значение отклонения d_i используют как оптимальное отклонение на следующем i+1 шаге:

шаг 1: при

шаг 2: при

Далее в зависимости от предъявляемых требований (критериев) эффективности:

а) если основным критерием эффективности предлагаемого способа является минимум интервальных оценок пеленгов сигналов (например, в случае близко направленных пеленгов), то лучше использовать нелинейное программирование для однокритериальной задачи, получаемой методом пороговой оптимизации;

б) если критичным показателем является время определения пеленга, то лучше применять квадратичное программирование для однокритериальной задачи, получаемой методом пороговой оптимизации;

в) если основным критерием эффективности является минимум интервальных оценок амплитуд (мощностей излучения) сигналов, то целесообразнее использовать архимедову модель из целевого программирования.

Если необходимо учесть сразу два показателя - минимум интервальных оценок для амплитуд сигналов и углов пеленгов, то лучшие результаты даст решение задачи минимизации энтропии. Для этого можно ввести дополнительную целевую функцию - энтропию - для получения трехкритериальной задачи:

при ограничениях или

Наибольший эффект дает вариант, когда функционалы J₁ и J₂ переведены в ограничения (метод пороговой оптимизации); то есть:

при

6. Итерационными вычислительными процедурами находят решение одной из задач математического программирования, выбранных в п.5.

7. По максимумам спектра мощности полученного углового спектра сигнала определяют азимут α и угол места β каждого луча принятого многолучевого сигнала.

8. Для уточнения полученных в п.7 точечных оценок используем способ получения интервальных оценок параметров ИРИ.

Ковариационную матрицу решения СЛАУ вида (3) (неизвестного вектора параметров) можно найти, используя теорему Крамера-Рао [2, С.380], если известна логарифмическая функция правдоподобия (логарифм совместной плотности вероятности входящих в рассмотрение измеренных величин -

Теорема Крамера-Рао гласит: В каждом случае регулярной оценки непрерывного типа квадрат среднего квадратического отклонения (СКО) оценки от истинного значения θ удовлетворяет неравенству

где lnL (x, θ) - натуральный логарифм функции правдоподобия L для выборки

x₁x₂…x_n.

Тогда ковариационная матрица решения имеет вид

где N - матрица, составленная из вторых производных логарифмической функции правдоподобия ln L, по всем элементам векторов α и β.

Поскольку на вектор действует аддитивный гауссовый шум со среднеквадратичным отклонением (СКО), равным σ, и нулевым математическим ожиданием, то подчиняется многомерному нормальному закону распределения вида:

где является математическим ожиданием вектора При найденных оценках и α_i и β_j, i=1, 2,…, M_α, j=1, 2,…, M_β выражение (4) будет являться функцией правдоподобия для Найдем натуральный логарифм выражения (4):

Тогда ковариационную матрицу оценок решения для азимутов, углов места и амплитуд определяем по формулам

В конце можно произвести построение и визуализацию пеленгационной панорамы, полученной на основе точечных и интервальных оценок амплитуд и пеленгов.

В качестве примера проверки реализации предлагаемого способа проведено имитационное моделирование на персональном компьютере с процессором Intel Celeron 2,00 ГГц с объемом оперативной памяти 512 МБ в математическом пакете Matlab 7.0.

Имитировались два сигнала с пеленгами α₁=56°25' и α₂=128°57' и амплитудами 10 и 12 мВ соответственно (β₁ и β₂ примем нулевыми). Полагали, что число элементов АС N+1=16, R=30, f₀=20 МГц. Для каждого метода своя оптимальная сетка по α.

На компоненты вектора действует аддитивный гауссовый шум с нулевым математическим ожиданием и СКО σ=0,5 мВ. Вектор везде один и тот же.

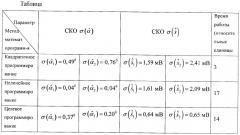
Пеленгационная панорама примера реализации способа представлена на фиг.1. СКО решений и и оценки времени счета (в сравнительных друг с другом относительных единицах по функции cputime пакета Matlab) выполнения способа с разными методами математического программирования: квадратичным, нелинейным и целевым, сведены в таблицу. Имитационное моделирование способа-прототипа [1] с такими же имитирующими сигналами после 10000 итераций не дало сходящегося решения.

Таким образом, преимуществами предлагаемого способа является следующее.

1. Повышение эффективности за счет учета дополнительных ограничений, налагаемых на решение и соответствующих физической постановке задачи, и за счет разных целевых функций.

2. Повышение надежности за счет получения интервальных оценок решения, позволяющие судить о возможном разбросе решений и, следовательно, о достоверности получаемых решений.

ИСТОЧНИКИ ИНФОРМАЦИИ

1. Патент РФ №2285938, МПК G01S 5/04, 2006 г.

2. Грешилов А.А. Математические методы принятие решений: Учеб. пособие для вузов. - М.: Изд-во МГТУ им. Н.Э.Баумана, 2006. - 584 с.

1. Способ пеленгования источников радиоизлучения на одной частоте, включающий прием многолучевого сигнала многоэлементной антенной решеткой, преобразование ансамбля принятых сигналов, зависящих от времени и номера антенного элемента, в цифровые сигналы, преобразование цифровых сигналов в сигнал , описывающий комплексное распределение амплитуд и фаз на элементах решетки, формирование двумерного сигнала комплексной фазирующей функции размером N×(M_α·M_β), описывающего возможные направления прихода от каждого потенциального источника на заданной частоте приема, где N - количество элементов антенной решетки, М_α - число угловых положений, соответствующих заданным потенциально возможным направлениям сигнала по азимуту α, М_β - число угловых положений, соответствующих заданным потенциально возможным направлениям прихода сигнала по углу места β, отличающийся тем, что получение углового спектра многолучевого сигнала осуществляют посредством задания сетки пеленгов принимаемых сигналов, формирования сигнала J₁ как суммы квадратов разности между сигналами h_i комплексного амплитудно-фазового распределения на каждом элементе антенной решетки и произведениями строк двумерного сигнала комплексной фазирующей функции на элементы сигнала , где i=1,2,…,N, j=1,2,…, М_α·М_β, и сигнала J₂, определяющего вид спектра мощности как суммы дробных степеней формирования целевой функции и ограничения из сигналовJ₁ и J₂ с последующим нахождением по максимумам спектра мощности углового спектра сигнала , точечных сигналов азимута α и угла места β, являющихся соответствующими точечными оценками, для каждого луча принятого многолучевого сигнала.

2. Способ по п.1, отличающийся тем, что дополнительно определяют интервальные оценки точечных сигналов с помощью обращения матрицы сигналов, элементы которой есть вторые частные производные сигнала, определяемого как квадрат разности двумерного сигнала комплексной фазирующей функции, умноженного на точечные оценки углового спектра сигнала , и сигнала комплексного амплитудно-фазового распределения на каждом элементе антенной решетки, по элементам вектора при найденных точечных оценках пеленгов и амплитуд.