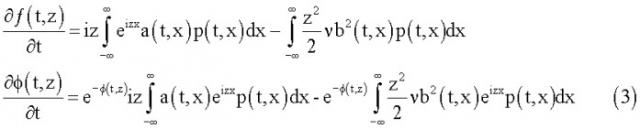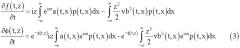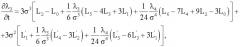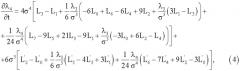Устройство адаптивного оценивания сосредоточенной помехи

Устройство адаптивного оценивания сосредоточенной помехи

Иллюстрации

Показать все

Реферат

Изобретение относится к радиосвязи и может использоваться в системах передачи как дискретных, так непрерывных сообщений по каналам связи, подверженных действию аддитивных помех.

Известно устройство [1, стр.276, рис.12.1], изображенное на фиг.1, содержащее последовательно соединенные адаптивный фильтр и сумматор, выход адаптивного фильтра соединен с первым входом сумматора, причем вход адаптивного фильтра является эталонным входом устройства, второй вход сумматора является сигнальным входом устройства, выход сумматора является выходом устройства и соединен с управляющим входом адаптивного фильтра.

Однако известное устройство имеет значительный недостаток, связанный с тем, что устройство требует для своей работы наличия дополнительного сигнала на эталонном входе устройства. Этот сигнал должен быть не коррелирован с входным сигналом, несущим информацию, и коррелирован с помехой, содержащейся вместе с входным сигналом на входе 1 устройства. Следует отметить, что на практике, чтобы найти подходящий эталонный сигнал, требуется решить ряд сложных задач и, если бы в действительности такой сигнал имелся, то адаптивная система была бы не нужна, можно было бы обойтись только вычитающим устройством. В условиях априорной неопределенности относительно свойств аддитивных помех данное устройство могло бы быть использовано в схеме разнесенного приема, когда сигнальный и эталонный входы устройства являются сигналами двух ветвей разнесения.

Наиболее близким по технической сущности к заявляемому устройству является устройство [1, стр.354, рис.13.15] для случая двух ветвей разнесения (К=2), изображенное на фиг.2, содержащее первый и второй адаптивные фильтры и сумматор, выходы адаптивных фильтров соединены с первым и вторым входами сумматора, причем входы адаптивных фильтров являются сигнальными входами двух ветвей разнесения, а выход сумматора соединен с управляющими входами адаптивных фильтров.

Недостаток данного устройства проявляется в том, что данное устройство также оказывается практически неработоспособным, как и аналог, в случае, когда сигналы и помехи в ветвях разнесения оказываются некоррелированными. Главным условием работоспособности устройства является наличие на его входах сильно коррелированных составляющих помех.

Сущность предлагаемого изобретения - улучшение качества адаптивного оценивания негауссовской сосредоточенной помехи, возможность работы в условиях априорной неопределенности относительно их свойств.

Эта сущность достигается тем, что в устройство адаптивного оценивания сосредоточенной помехи, содержащее первый и второй адаптивные фильтры и сумматор, выходы адаптивных фильтров соединены с первым и вторым входами сумматора, введены блок вычисления отсчетов корреляционной функции, блок вычисления коэффициентов управления адаптивных фильтров, первый и второй сумматоры, первый и второй блоки вычисления кумулянтов, причем входами устройства являются первый и второй входы блока вычисления отсчетов корреляционной функции, первый выход которого подключен к входу первого адаптивного фильтра и к первому входу первого сумматора, второй выход блока вычисления отсчетов корреляционной функции подключен к входу второго адаптивного фильтра и к первому входу второго сумматора, третий выход блока вычисления отсчетов корреляционной функции соединен с первым входом блока вычисления коэффициентов управления адаптивных фильтров, второй вход которого соединен с выходом первого блока вычисления кумулянтов, третий вход блока вычисления коэффициентов управления адаптивных фильтров соединен с выходом второго блока вычисления кумулянтов, а выход подключен к управляющим входам первого и второго адаптивных фильтров, выход первого сумматора соединен с входом первого блока вычисления кумулянтов, а выход второго сумматора соединен с входом второго блока вычисления кумулянтов, выходом устройства является выход сумматора, который подключен к четвертому входу блока вычисления коэффициентов управления адаптивных фильтров, ко второму входу первого сумматора, ко второму входу второго сумматора.

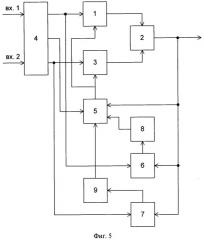
На фиг.1 представлена функциональная схема адаптивного фильтра (аналог); на фиг.2 представлена функциональная схема матричного адаптивного фильтра (прототип); на фиг.3 представлена функциональная схема блока вычисления отсчетов корреляционной функции; на фиг.4 представлена функциональная схема блока вычисления кумулянтов; на фиг.5 представлена функциональная схема предлагаемого устройства.

Устройство адаптивного оценивания сосредоточенной помехи (фиг.5) содержит первый адаптивный фильтр 1, сумматор 2, второй адаптивный фильтр 3, блок 4 вычисления отсчетов корреляционной функции, блок 5 вычисления коэффициентов управления адаптивных фильтров, первый сумматор 6, второй сумматор 7, первый блок вычисления кумулянтов 8, второй блок вычисления кумулянтов 9.

Входами устройства адаптивного оценивания сосредоточенной помехи являются первый и второй входы блока 4 вычисления отсчетов корреляционной функции, первый выход которого подключен к входу первого адаптивного фильтра 1 и к первому входу первого сумматора 6, второй выход блока 4 вычисления отсчетов корреляционной функции подключен к входу второго адаптивного фильтра 3 и к первому входу второго сумматора 7, третий выход блока 4 вычисления отсчетов корреляционной функции соединен с первым входом блока 5 вычисления коэффициентов управления адаптивных фильтров, второй вход которого соединен с выходом первого блока 8 вычисления кумулянтов, третий вход блока 5 вычисления коэффициентов управления адаптивных фильтров соединен с выходом второго блока 9 вычисления кумулянтов, а выход подключен к управляющим входам первого 1 и второго 3 адаптивных фильтров, выход первого сумматора 6 соединен с входом первого блока 8 вычисления кумулянтов, а выход второго сумматора 7 соединен с входом второго блока 9 вычисления кумулянтов, выходом устройства является выход сумматора 2, который подключен к четвертому входу блока 5 вычисления коэффициентов управления адаптивных фильтров, ко второму входу первого сумматора 6, ко второму входу второго сумматора 7.

Устройство работает следующим образом.

В условиях априорной неопределенности относительно свойств сосредоточенных помех рассмотрим один из возможных способов обработки принимаемой смеси полезного сигнала S(t), сосредоточенной помехи ξ(t) и флуктуационного гауссовского шума n(t), основанного на использовании адаптивной фильтрации совместно с разнесенным приемом.

Пусть полезный сигнал, помеха и шум являются стационарными случайными процессами, а сигналы двух ветвей разнесения z₁(t) и z₂(t) подаются соответственно на вх.1 и вх.2 устройства фиг.1:

z₁(t)=S₁(t)+ξ₁(t)+n₁(t);

z₂(t)=S₂(t)+ξ₂(t)+n₂(t).

Причем предполагается независимость S_i(t) от ξ_i(t), i, j=1,2 и от белых шумов n₁(t) и n₂(t). Будем считать, что ξ(t) являются негауссовским случайным процессом.

Известно [1], что в схеме, представленной на фиг.1, адаптивный фильтр (АФ) - блок 1, изменяющий свою импульсную характеристику под воздействием выходного сигнала, например по алгоритму наименьших квадратов, отфильтровывает из сигнала на втором входе сумматора 2 все составляющие, коррелированные с сигналом на входе АФ, по критерию минимума среднеквадратической ошибки. В [3] был произведен анализ работы рассматриваемого АФ, из которого следует, что применение адаптивной фильтрации при малом уровне белых шумов на основном и эталонном входе весьма эффективна для ситуации разнесенного приема, когда полезные сигналы в разных ветвях разнесения некоррелированные при сильно коррелированных сосредоточенных помехах.

Приведенные в [3] характеристики работы аналога полностью совпадают с характеристиками прототипа, представленного на фиг.2. Основное отличие между ними заключается в алгоритме перестройки весовых коэффициентов адаптивных фильтров прототипа. Этот алгоритм предполагает наличие известной корреляционной функции сосредоточенной помехи в месте приема. В этом случае нет никакой необходимости в наличии эталонного сигнала.

Известно [2], что в схемах, представленных на фиг.1 и фиг.2, после окончания процесса адаптации в режиме слежения за медленными изменениями корреляционных свойств сигнала на входе АФ, АФ идентичен фильтру Колмогорова - Винера [2], который дает оптимальную оценку только для гауссовской помехи ξ(t). При негауссовской ξ(t) повысить качество оценок, даваемых адаптивной фильтрацией, можно, если при разработке алгоритма адаптивной фильтрации учитывать кумулянты выше второго порядка.

В качестве подтверждения эффективности использования кумулянтов высокого порядка рассмотрим задачу оценивания центральных моментов негауссовского случайного процесса, который моделируется как выходной сигнал нелинейной системы при подаче на ее вход белого гауссовского шума. При этом случайный процесс может быть описан дифференциальным уравнением

где n(t) - белый гауссовский шум с интенсивностью ν.

При заданном распределении начального условия x₀ требуется определить несколько центральных моментов m₁(t)=Mx_t, m_k(t)=M[x_t-m₁(t)]^k, (k=2, 3, …, l).

Решение поставленной задачи основано на составлении системы дифференциальных уравнений для кумулянтов при условии, что плотность вероятности случайного процесса x(t) описывается уравнением Фоккера-Планка-Колмогорова

Пусть x(t) является решением в момент времени t дифференциального уравнения (1). Известно, что k-й кумулянт случайной величины x(t) в момент t равен

где

Следовательно, для того чтобы написать дифференциальное уравнение для λ_k(t), k=1, 2, …, m, необходимо дифференциальное уравнение для ϕ(t, z), которое в свою очередь можно получить из дифференциального уравнения для ƒ(t, z).

Дифференциальные уравнения для ϕ(t, z) и ƒ(t, z) соответственно имеют вид [4]

Дифференцируя (3) по z k раз с учетом (2) и представив плотность вероятности p(t, x) рядом Эджворда, можно получить уравнения для кумулянтов. В качестве примера выпишем систему уравнений для четырех кумулянтов, приняв гипотезу о том, что кумулянты процесса x(t) порядка выше четвертого равны нулю

где

σ²=λ₂.

Рассмотрим пример оценивания дисперсии случайного процесса x(t), являющегося кубическим преобразованием нормального марковского процесса, методом, основанным на решении системы дифференциальных уравнений (4) при аппроксимации плотности вероятности p(t, x) эксцессным распределением, дает более точное значение по сравнению с результатом, полученным при гауссовской аппроксимации.

Зададим нормальный марковский процесс стохастическим дифференциальным уравнением первого порядка вида (стохастический дифференциал понимается в смысле Ито) [5]

Тогда стохастический дифференциал скалярной действительной непрерывной функции y(t)=x³(t), обладающей ограниченными первыми и вторыми производными, где вторые производные удовлетворяют условиям Липшица, определяется формулой Ито [5]. Таким образом, дифференциал для процесса y(t) имеет вид

Подставляя найденные выражения функций a(t, y_t) и b(t, y_t) в (4), получим систему дифференциальных уравнений, которые описывают плотность вероятности процесса y(t) для эксцессного распределения.

Для гауссовкого распределения система дифференциальных уравнений имеет вид

Так как в установившемся состоянии аналитического решения систем нелинейных дифференциальных уравнений (4) и (7) найти невозможно, то для решения систем были использованы численные методы. Один из возможных численных методов решения задачи является метод установления [6]. В этом случае для решения стационарной задачи строится нестационарный процесс, решение которого с течением времени оказывается независимым от него и устанавливается к решению исходной стационарной задачи. При этом для упрощения вычислений интегралы L_k и , входящие в правую часть (4) и (7), определяются с использованием сплайн аппроксимации выражений для a(t, y_t) и νb²(t, y_t)

где

a ₀, a ₁, a ₂, a ₃ - коэффициенты кубического сплайна, аппроксимирующего функцию a(t, y_t) на интервале [z_k, z_k+1]. Аналогично определяются коэффициенты для функции b(t, y_t).

При интенсивности белого шума ν=1 и начальных условиях: λ₁=0, λ₂=1, λ₃=0, λ₄=0 в установившемся состоянии значения дисперсии равны при учете четырех кумулянтов, при учете кумулянтов.

В данном примере можно оценить точность полученного решения, так как в установившемся состоянии плотность вероятности определяется выражением [7]

Используя выражение (8) для плотности, можно вычислить точное значение для дисперсии процесса y(t)

При данных параметрах процесса λ₂=1.875.

Таким образом показано, что ошибка в вычислении дисперсии при гауссовой аппроксимации распределения случайного процесса составляет 59%, а при эксцессном приближении 13%.

Улучшим оценку негауссовского процесса, полученную матричным фильтром (фиг.2), в схеме фильтрации на фиг.5 при помощи введения кумулянтов выше второго порядка в рабочую функцию АФ, предварительно оценив корреляционную функцию процесса ξ(t), которая при разнесенном приеме в предположении некоррелированности полезных сигналов в разных ветвях разнесения и при сильной корреляции сосредоточенных помех может быть получена согласно фиг.3, аналогично тому, как это сделано в [3]. Оценка отсчетов функции корреляции (выход блока 4 вычисления отсчетов корреляционной функции) при этом может быть определена, например, в виде

где z(t_j) - значение сигнала на j-м отводе линии задержки ЛЗ, а К определяется полосой частот ожидаемой сосредоточенной помехи ξ(t).

Блок 5 вычисления коэффициентов управления адаптивных фильтров функционирует по алгоритму, являющемуся симбиозом алгоритма Гриффитса [1] и алгоритма, приведенного в [8], т.е. весовые коэффициенты адаптивных фильтров изменяются по следующему алгоритму

где и - векторы весовых коэффициентов соответственно первого и второго адаптивных фильтров;

- оценка отсчета сосредоточенной помехи;

и - отсчет разностных сигналов поступающих в блок 5 вычисления коэффициентов управления адаптивных фильтров из блока 8 и блока 9 соответственно;

Р^Т=[r₀ r₁…r_N]^T - вектор оценок отсчетов корреляционной функции процесса ξ(t).

Коэффициенты c₃ и c₅, входящие в (9), определяются выражениями

λ₂, λ₄, λ₆ - оценки кумулянтов полезного сигнала S(t), которые вычисляются в блоках 8 и 9, представленных на фиг.5.

Оценка кумулянтов полезного сигнала (фиг.4) при этом может быть определена, например, в виде

где

Таким образом, учет кумулянтов выше второго порядка при разработке адаптивного алгоритма позволит повысить фильтрацию негауссовских процессов.

Литература

1. Уидроу Б., Стринз С. Адаптивная обработка сигналов: Пер. с англ. - М.: Радио и связь, 1989. - 440 с.

2. Ван Трис Г. Теория обнаружения, оценок и модуляции: Пер. с англ. - М.: Советское радио, 1972, 744 с.

3. Патент РФ №2160498. Устройство адаптивного подавления помех / Карташевский В.Г., Мишин Д.В. - Опубл. в БИ №34, 2000.

4. Пугачев B.C., Синицын И.Н. Теория стохастических систем. М.: Логос, 2004. - 1000 с.

5. Тихонов В.И., Кульман Н.К. Нелинейная фильтрация и квазикогерентный прием сигналов. М.: Сов. Радио, 1975. - 704 с.

6. Бахвалов Н.С.Численные методы / Бахвалов Н.С., Жидков Н.П., Кобельников Г.М. - 4-е изд. - М.: БИНОМ. Лаборатория знаний, 2006. - 636 с.

7. Тихонов В.И., Миронов М.А. Марковские процессы. М.: Сов. Радио, 1977. - 488 с.

8. Т.Y. Al-Naffouri, A.H. Sayed, "Adaptive filters with error nonlinearities: mean-square analysis and optimum design", EURASIP journal on applied Signal Processing 2001:4, 192-205.

Устройство адаптивного оценивания сосредоточенной помехи, содержащее первый и второй адаптивные фильтры и сумматор, выходы адаптивных фильтров соединены соответственно с первым и вторым входами сумматора, отличающееся тем, что введены блок вычисления отсчетов корреляционной функции, блок вычисления коэффициентов управления адаптивных фильтров, первый и второй сумматоры, первый и второй блоки вычисления кумулянтов, причем входами устройства являются первый и второй входы блока вычисления отсчетов корреляционной функции, первый выход которого подключен к входу первого адаптивного фильтра и к первому входу первого сумматора, второй выход блока вычисления отсчетов корреляционной функции подключен к входу второго адаптивного фильтра и к первому входу второго сумматора, третий выход блока вычисления отсчетов корреляционной функции соединен с первым входом блока вычисления коэффициентов управления адаптивных фильтров, второй вход которого соединен с выходом первого блока вычисления кумулянтов, третий вход блока вычисления коэффициентов управления адаптивных фильтров соединен с выходом второго блока вычисления кумулянтов, а выход подключен к управляющим входам первого и второго адаптивных фильтров, выход первого сумматора соединен с входом первого блока вычисления кумулянтов, а выход второго сумматора соединен с входом второго блока вычисления кумулянтов, выходом устройства является выход сумматора, который подключен к четвертому входу блока вычисления коэффициентов управления адаптивных фильтров, ко второму входу первого сумматора, ко второму входу второго сумматора.