Способ многосигнальной пеленгации источников радиоизлучения на одной частоте

Способ многосигнальной пеленгации источников радиоизлучения на одной частоте

Иллюстрации

Показать все

Реферат

Изобретение относится к радиотехнике, в частности к радиопеленгации, и может быть использовано в системах определения направления на источники радиоизлучения, работающие на одной частоте.

Уровень техники

Многосигнальная пеленгация источников радиоизлучения (ИРИ) имеет место в процессе мониторинга радиоэлектронной обстановки при многолучевом распространении радиоволн, воздействии преднамеренных и непреднамеренных помех, отражениях сигнала от различных объектов и слоев атмосферы.

Задача радиопеленгации в общем случае является некорректной в математическом плане. Большинство известных способов многосигнальной пеленгации на одной частоте опираются на статистические методы проверки гипотез, на метод максимума правдоподобия, на сверхразрешающие методы (например, MUSIC - multiple signal classification) и др. Однако задача пеленгации ИРИ как некорректная задача не может быть решена надежно ни статистическими методами, достоверность результата которых определяется точностью полученных оценок параметров сигналов; ни методом наименьших квадратов (МНК) в силу нелинейности и плохой обусловленности решаемой системы уравнений; ни сверхразрешающими методами, которые дают приемлемые результаты лишь при высоких соотношениях сигнал/шум и не обеспечивают разрешение ИРИ, имеющих близкие по значениям пеленги.

Известен способ пеленгации с повышенной разрешающей способностью [1] со следующей последовательностью действий:

1. Принимают многолучевой сигнал антенной системой, состоящей из М элементов и формируют ансамбль сигналов х_m(t), m=1; 2; …; М, зависящих от времени t.

2. Синхронно преобразуют ансамбль принятых сигналов х_m(t) в цифровые сигналы

x_m(z), где z - номер временного отсчета сигнала.

3. Преобразуют цифровые сигналы x_m(z) в сигнал комплексного амплитудно-фазового распределения (АФР) описывающий амплитуды и фазы сигналов, принятых элементами АС. Запоминают АФР

4. Генерируют и запоминают идеальный двумерный сигнал комплексной фазирующей функции размером M×N, зависящий от заданной частоты приема и описывающий возможные направления прихода сигнала от каждого потенциального источника, где N - число угловых положений, соответствующих заданным потенциально возможным направлениям прихода сигналов по азимуту θ_n и углу места β_n, где n=1; 2; …; N - номер направления.

5. Используя вектор АФР и сигнал фазирующей функции , синтезируют по известной операции псевдообращения начальное приближение углового спектра сигнала , где Т - обозначение операции комплексно-сопряженного транспонирования.

6. Восстанавливают угловой спектр мощности углового спектра сигнала , k≥1, полученного на предыдущей итерации. При восстановлении углового спектра на первой итерации используется начальное приближение , на второй итерации - и т.д.

7. Возводя смещенное на малую положительную величину полученное приближение углового спектра мощности в степень (1-р/2), формируют зависящий от предыдущего решения двумерный взвешивающий сигнал размером N×N в форме диагональной матрицы где р<1, - m-й элемент вектора , ε - малое число.

8. Используя полученный взвешивающий сигнал и сигналы и формируют взвешенный сигнал фазирующей функции , сигнал весовых коэффициентов , взвешивающий сигнал АФР , вектор взвешенного АФР и зависящий от предыдущего решения текущий угловой спектр сигнала .

9. Сравнивают энергию разности угловых спектров , полученных на текущей и предыдущей итерациях, с порогом δ.

10. При невыполнении условия инициализируется очередная итерация синтеза углового спектра, на которой повторяются операции из пунктов 8 и 9. При выполнении условия восстанавливают спектр мощности углового спектра сигнала полученного на текущей итерации синтеза, по максимумам которого определяют азимутальные и угломестные пеленги каждого луча принятого многолучевого сигнала.

Этот способ обладает следующими недостатками:

- Угловой спектр получают по формуле , где , p<1, что не гарантирует устойчивости решения к малым вариациям сигнала Поскольку сигнал получают на основе физических измерений, он неизбежно содержит в себе помеху. Таким образом, невозможно гарантировать устойчивое получение углового спектра .

- Нет гарантии выполнения условия вхождения в «пороговую трубку» энергии разности угловых спектров за конечное число итераций.

- Результатом итерационного процесса является точечная оценка углового спектра , которая не позволяет судить о ее надежности, т.к. имеет место помеха в сигнале АФР , а также в сигнале фазирующей функции (несущая частота и геометрические параметры АС также содержат погрешности).

Указанные недостатки очевидно не позволят применять способ в реальных условиях из-за его недопустимо низкой практической надежности и точности пеленгации и отсутствия возможности оценки надежности полученного результата.

Раскрытие изобретения

Предлагаемый способ свободен от указанных недостатков и является более надежной и эффективной реализацией параметрического метода многосигнального пеленгования на одной частоте.

Достигаемый технический результат - повышение надежности и точности пеленгации при приеме радиосигналов нескольких источников радиоизлучения, работающих на одной частоте, с использованием антенных систем (АС), состоящих из слабонаправленных элементов (вибраторов), а также расширение функциональных возможностей способа за счет дополнительного определения интервальных оценок амплитуд сигналов и пеленгов источников радиоизлучения.

Способ многосигнальной пеленгации источников радиоизлучения на одной частоте включает в себя прием многолучевого сигнала посредством многоэлементной антенной системы (АС), синхронное преобразование ансамбля принятых сигналов, зависящих от времени и номера элемента АС, в цифровые сигналы, преобразование цифровых сигналов в сигнал амплитудно-фазового распределения (АФР), описывающий распределение амплитуд и фаз на элементах АС, вычисление сигнала фазирующей функции А. Предлагаемый способ отличается тем, что получение углового спектра осуществляют введением переопределенного базиса посредством сетки пеленгов для формирования из исходной системы нелинейных уравнений системы линейных алгебраических уравнений (СЛАУ) и решением этой системы посредством минимизации регуляризирующего l_p-функционала.

Для минимизации указанного l_p-функционала в качестве начального приближения могут брать решение, полученное методом регуляризации А.Н.Тихонова.

Дополнительно для надежности результатов определяют интервальную оценку углового спектра на основе ковариационной матрицы, полученной по теореме Крамера-Рао с использованием в качестве функции правдоподобия указанного l_p- функционала.

Результаты оценок пеленгов далее можно представлять в визуальном графическом виде для последующего принятия решений по ним.

Перечень фигур

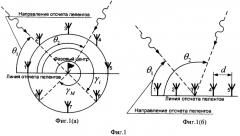
Фиг.1. Пространственные конфигурации рассматриваемых АС.

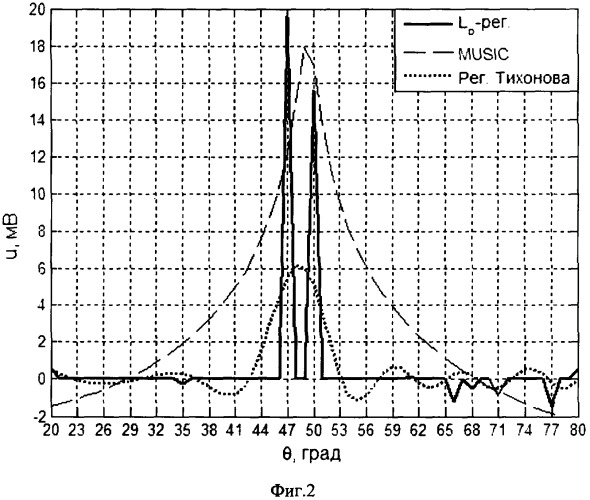
Фиг.2. Сравнительные графики пеленгационных панорам, полученных в примере предлагаемым способом и способами MUSIC и регуляризации А.Н.Тихонова.

Осуществление изобретения

В качестве многоэлементной АС рассматриваем две системы, состоящие из нескольких слабонаправленных элементов (вибраторов): круговую АС (фиг.1а) и линейную АС (фиг.1б). В круговой АС (фиг.1а) в качестве фазового центра (точки, относительно которой происходит измерение фаз сигналов, приходящих на элементы антенной системы) берем центр окружности. В линейной АС (фиг.1б) в качестве фазового центра выбираем один из вибраторов.

Необходимо определение следующих параметров ИРИ, присутствующих в эфире: количество; амплитуды (мощности) излучаемых сигналов; азимутальные пеленги и угломестные пеленги.

В качестве практически оправданного допущения для предлагаемого способа сигналы рассматривают как детерминированные, подверженные аддитивной помехе, оценки параметров которых подлежат определению.

Поскольку на результаты измерений неизбежно накладывается помеха, а также имеют место ошибки измерений, обусловленные используемой аппаратурой, дополнительно желательно получить не только точечные оценки искомых параметров, но и их ковариационные матрицы или, по крайней мере, дисперсии, для получения интервальных оценок.

Полагаем, что в эфире присутствует К штук ИРИ с азимутальными пеленгами угломестными пеленгами и амплитудами (мощностями) излучаемых сигналов ; - сигнал комплексного АФР, описывающий амплитуды и фазы сигналов, принятых элементами АС, где М - количество элементов АС. Используемый вид модуляции (амплитудная, частотная, фазовая и др.) не имеет принципиального значения.

В общем случае исходная система нелинейных уравнений относительно неизвестных θ, β и u имеет следующий вид:

где n(t) - вектор аддитивной помехи, имеющей нулевое математическое ожидание и ковариационную матрицу вида σ²I, I - единичная матрица, σ - среднеквадратическое отклонение (СКО); матрица А(θ, β, t) (фазирующая функция) формируется с учетом вида сигналов пеленгуемых ИРИ и пространственной конфигурации АС.

Для круговой антенной системы (фиг.1а) матрица А(θ, β, t) имеет вид:

где m - й элемент, m=1; 2; …; М, вектора-столбца a(θ_k, β_k, t) имеет вид

Для линейной антенной системы (фиг.1б) с фазовым центром, расположенным на вибраторе №1, матрица А(θ,t) имеет вид

где: f₀ - частота сигналов, излучаемых пеленгуемыми ИРИ,

φ_k - начальная фаза k -гo сигнала,

R - радиус окружности, вдоль которой расположены элементы антенной системы,

λ - длина волны сигналов ИРИ,

d - расстояние между соседними элементами антенной системы,

γ_i, i=1; 2; …; М - угол между линией отсчета пеленгов и линией, проведенной через центр окружности и i-й элемент антенной системы (для круговой АС),

М - количество элементов в антенной системе.

Требуется определить для каждого из одновременно поступивших на АС сигналов амплитуду (мощность) u_k, азимутальный пеленг θ_k и угломестный пеленг β_k.

Линеаризуем нелинейную модель (1) при помощи введения переопределенного базиса посредством сетки пеленгов. Будем считать, что задан интервал возможных значений азимутальных пеленгов (например, от 0° до 180°) и угломестных пеленгов (например, от 0° до 90°). Введем на данном интервале сетку пеленгов и сетку углов места . В системе (1) матрицу А(θ, β, t) заменим матрицей :

в которой неизвестными остаются только амплитуды, соответствующие азимутальным пеленгам и угломестным пеленгам .

Получаем СЛАУ относительно вектора неизвестных u:

Количество элементов вектора амплитуд сигналов u (количество столбцов матрицы системы) увеличивается до произведения размерностей сеток азимутальных и угломестных пеленгов - N_θ×N_β. Теперь вектор u представляет собой распределение амплитуд (мощностей) по пеленгам (угловой спектр). В идеальном случае (шумы отсутствуют) количество ненулевых элементов вектора u равно количеству фактически присутствующих в эфире ИРИ. Положение ненулевых элементов в векторе u (в сетке пеленгов) характеризует пеленги соответствующих ИРИ.

Таким образом, введение сетки пеленгов решает не только проблему нелинейности задачи, но и проблему определения количества ИРИ. Решив СЛАУ (5), получаем необходимую информацию по пеленгам.

Несмотря на линейность задача решения СЛАУ (5) является вычислительно некорректной. Поэтому для ее решения необходимо применение специфических методов, например методов регуляризации. Следует обратить внимание, что количество узлов сетки много больше количества ИРИ, т.е. большинство элементов вектора u в идеальном случае равно нулю. При решении такого рода задач хорошие результаты показывает метод l_p-регуляризации [2].

В l_р-регуляризации для нахождения решения строят l_р-функционал вида:

Регуляризирующий l_p-функционал вида (6) способствует получению вектора решения, большинство элементов которого равны нулю, а несколько элементов имеют относительно большие значения. Значение параметра регуляризации λ определяют в процессе калибровки пеленгатора.

Для нахождения оптимального значения функционала (6) можно использовать любой метод минимизации (глобальной или локальной), в качестве начального приближения для которого в том числе берут результат, полученный методом регуляризации А.Н.Тихонова [3].

Приведем способ получения интервальных оценок параметров ИРИ.

Сначала считаем, что матрица системы (5) известна точно (погрешность присутствует только в векторе АФР y).

Ковариационную матрицу решения СЛАУ вида (5) (неизвестного вектора параметров) можно найти, используя теорему Крамера-Рао [4, с.380], если известна логарифмическая функция правдоподобия (логарифм совместной плотности вероятности входящих в рассмотрение измеренных величин - ln L (y, u, θ, β) [4, с.382].

Теорема Крамера-Рао гласит: В каждом случае регулярной оценки непрерывного типа квадрат среднего квадратического отклонения (СКО) оценки от истинного значения θ удовлетворяет неравенству

где ln L(x, θ) - натуральный логарифм функции правдоподобия L для выборки x₁ x₂…x_n.

Тогда ковариационная матрица решения имеет вид

где N - матрица, составленная из вторых производных логарифмической функции правдоподобия ln L по всем элементам векторов u, θ и β.

где

Значения элементов ковариационной матрицы (7) зависят от значений точечных оценок параметров , и которые найдем методом l_p-регуляризации. Дисперсии (диагональные элементы матрицы (7)) обладают свойством минимальности.

Установим связь между регуляризирующим функционалом J (u, λ) вида (6) и логарифмической функцией правдоподобия ln L(y, u, θ, β). Будем считать, что элементы вектора у распределены по нормальному закону с математическим ожиданием Аu и среднеквадратическим отклонением σ, а элементы вектора u подчиняются закону распределения вида с нулевым математическим ожиданием и тем же СКО (положим σ_u=σ); С - нормирующий множитель. Тогда функция правдоподобия L имеет вид

Прологарифмируем (8). Оценки , доставляющие максимум функциям L(y, u, θ, β) и ln L(y, u, θ, β), совпадают в силу монотонности логарифмической функции

Постоянное слагаемое можно не учитывать, т.к. оно не влияет на точечную оценку , доставляющую максимум функции правдоподобия (9). Величины σ и σ_u=σ не влияют на величины точечных оценок искомых параметров, чего нельзя сказать об их дисперсиях. С учетом этого для получения точечных оценок искомых параметров u выражение (9) можно записать следующим образом:

Введем обозначение Тогда (10) запишется в следующем виде

Таким образом, ковариационную матрицу решения, полученного методом l_p-регуляризации, будем вычислять по формуле (7), подставляя в нее вместо функции ln L(y, u, θ, β), целевую функцию l_p-регуляризации, умноженную на величину , и найденные оценки параметров , и . На основе ковариационной матрицы построим соответствующие доверительные интервалы.

Перейдем к случаю, когда в задаче пеленгации погрешности присутствуют СЛАУ (5) и в правой части (электромагнитные помехи), и в левой части (погрешность определения несущей частоты f₀, погрешности измерения геометрических параметров АС). Все погрешности рассматриваем как аддитивные, имеющие нулевое математическое ожидание и известную дисперсию. В случае наличия погрешностей как в правой, так и в левой частях СЛАУ (5) необходимо внести соответствующие изменения в функцию правдоподобия. Изменения коснутся лишь вида нормы ; вместо нее в функцию правдоподобия нужно подставлять величину

.

Повышение надежности и точности пеленгации обусловлено использованием процедуры l_p-регуляризации для решения СЛАУ (5) [2], которая в данном случае более эффективна, чем процедура, предлагаемая в способе-прототипе.

В практическом плане способ осуществляют следующим образом.

1. Принимают многолучевой сигнал антенной системой, состоящей из М элементов и формируют ансамбль сигналов , зависящих от времени t.

2. Синхронно преобразуют ансамбль принятых сигналов x_m(t) в цифровые сигналы

х_m(z), где z - номер временного отсчета сигнала.

3. Преобразуют цифровые сигналы х_m(z) в сигнал комплексного амплитудно-фазового распределения (АФР) у, описывающий амплитуды и фазы сигналов, принятых элементами АС. Запоминают АФР у.

4. Генерируют и запоминают идеальный двумерный сигнал А комплексной фазирующей функции размером M×N, зависящий от заданной частоты приема и описывающий возможные направления прихода сигнала от каждого потенциального источника, где N - число угловых положений, соответствующих заданным потенциально возможным направлениям прихода сигналов по азимуту θ_n и углу места β_n, где n=1; 2; …; N - номер направления.

5. Используя вектор АФР у и сигнал фазирующей функции А, формируют l_p-функционал вида (6) и минимизируют его по параметрам u любым методом локальной минимизации, в качестве начального приближения для которого в том числе берут решение, полученное методом регуляризации А.Н.Тихонова [3, с.110-127], получая таким образом точечные оценки амплитуд сигналов и пеленгов источников радиоизлучения.

6. Используя полученные в п.5 точечные оценки амплитуд и пеленгов, получают соответствующие интервальные оценки на основе ковариационной матрицы, полученной по теореме Крамера-Рао [4, с.380] с использованием в качестве функции правдоподобия l_p-функционала вида (6).

7. Производят построение и визуализацию пеленгационной панорамы, полученной на основе точечных и интервальных оценок амплитуд и пеленгов, полученных в пп.5 и 6 соответственно.

Приведем модельный пример работы предлагаемого способа.

Рассмотрим пеленгацию двух ИРИ, работающих на частоте 20 МГц, имеющих близкие по значениям пеленги θ=[47° 50°]^Т, углы места β=[0° 0°]^Т и амплитуды u=[20 мВ 15 мВ]^T. Помеха имеет математическое ожидание, равное нулю, и СКО σ=3 мВ. Пеленгацию будем осуществлять в диапазоне пеленгов |20°; 80°| посредством линейной АС, состоящей из 16 вибраторов, отстоящих друг от друга на расстояние, равное половине длины волны сигнала (7,5 м). Шаг сетки пеленгов положим равным 1°.

Пеленгационная панорама, полученная в результате решения, приведена на фиг.2. Точечные оценки параметров сигналов получены методом l_p-регуляризации при р=0,9, λ=1. Приведены СКО оценок амплитуд сигналов и азимутальных пеленгов ИРИ , полученные по формуле (7). Для сравнения приведены СКО амплитуд, полученные методом статистических испытаний в 100 экспериментах.

Также на фиг.2 приведены результаты пеленгационных панорам, полученные не только методом l_p-регуляризации, но и широко распространенными методами MUSIC и регуляризации А.Н.Тихонова.

Точечные оценки параметров ИРИ:

СКО оценок, полученные по формуле (7):

СКО оценок, полученные методом статистических испытаний:

Таким образом, из приведенного примера достаточно наглядно видно преимущество (по сравнению с традиционными способами) повышения надежности и точности по предлагаемому способу с определением интервальных оценок амплитуд и пеленгов.

Источники информации

1. Патент РФ №2285938, МПК G01S 5/04, 2006 г.

2. M.Cetin and W.C.Karl Feature-enhanced synthetic aperture radar image formation based on nonquadratic regularization. IEEE Trans. Image Processing, vol. 10, no.4, pp.623-631. Apr.2001.

3. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. - М.: Наука, 1979.

4. Грешилов А.А. Математические методы принятия решений: Учеб. пособие для вузов. - М.: Изд-во МГТУ им. Н.Э.Баумана, 2006. - 584 с.

1. Способ многосигнальной пеленгации источников радиоизлучения на одной частоте, включающий в себя прием многолучевого сигнала посредством многоэлементной антенной системы (АС), синхронное преобразование ансамбля принятых сигналов, зависящих от времени и номера элемента АС, в цифровые сигналы, преобразование цифровых сигналов в сигнал амплитудно-фазового распределения АФР у, описывающий распределение амплитуд u и фаз φ сигналов на элементах АС, определения двумерного сигнала А комплексной фазирующей функции размером М×N, зависящего от заданной частоты приема и описывающего возможные направления прихода сигнала от каждого потенциального источника, где М - число элементов АС, N - число угловых направлений, соответствующих заданным потенциально возможным направлениям сигнала по азимуту θ_n и углу места β_n, где n=1; 2; …; N, отличающийся тем, что получение многосигнального углового спектра и вектора амплитуд сигналов u, представляющего собой распределение амплитуд по пеленгам θ_n и β_n, осуществляют путем формирования точечных оценок амплитуд и пеленгов сигналов за счет использования l_p-функционала, включающего в себя сумму квадратов разности сигнала А, умноженного на амплитуду искомого сигнала АФР у, минимизации его по параметрам u, с обеспечением соответствия решения по нахождению u результатам измерений у, с добавлением амплитуды искомого сигнала в степени p, где 0<p≤1, умноженной на параметр регуляризации γ, определяемый в процессе калибровки пеленгаторов, по полученному многосигнальному угловому спектру и вектору амплитуд сигналов строят пеленгационную панораму, по которой определяют количество, интенсивность и пеленги источников радиоизлучения.

2. Способ по п.1, отличающийся тем, что дополнительно определяют интервальную оценку амплитуд и пеленгов сигналов путем обращения матрицы, полученной из вторых производных от логарифмической функции правдоподобия InL, которая представляет собой l_p-функционал, при найденных оценках пеленгов и амплитуд, при этом построение пеленгационной панорамы осуществляют с учетом интервальных оценок амплитуд и пеленгов сигналов.