Способ уменьшения нагрузок и вибраций на летательных аппаратах, имеющих многолопастные воздушные винты с четным числом лопастей

Способ уменьшения нагрузок и вибраций на летательных аппаратах, имеющих многолопастные воздушные винты с четным числом лопастей

Иллюстрации

Показать все

Реферат

Изобретение относится к авиационной технике, а именно к проектированию и летным испытаниям воздушных винтов, устанавливаемых на летательных аппаратах (ЛА), преимущественно на вертолетах, самолетах и автожирах, и может быть использовано для увеличения ресурса конструкции ЛА по условиям усталостной прочности (валов несущих, рулевых, тянущих и толкающих винтов, главных, рулевых и промежуточных редукторов, подредукторных рам, фюзеляжей, хвостовых и килевых балок).

Уровень техники

Известно, что силы и моменты, создаваемые каждой из лопастей воздушного винта, обуславливаются аэродинамическими нагрузками и возникающими при ее колебаниях инерционными силами и моментами. Нагрузки с лопастей передаются на втулку винта и складываются на ней по определенным правилам, а затем, трансформируясь по другим правилам, передаются на фюзеляж (Михеев Р.А. Прочность вертолетов. М.: Машиностроение, 1984. с.30).

Для облегчения понимания дальнейшего изложения сущности изобретения рассмотрим сначала процесс сложения и трансформации гармоник на классическом воздушном винте, т.е. на винте с равномерным расположением лопастей по диску (Михеев Р.А. Прочность вертолетов. М.: Машиностроение, 1984. с.30). При выводе правил суммирования обычно принимается, что лопасти идентичны по своим аэродинамическим, массовым и жесткостным характеристикам. При этом условии законы изменения нагрузок на отдельных лопастях будут отличаться друг от друга только сдвигом по времени (фазе). Амплитуды любой из составляющих гармоник для всех лопастей будут одинаковыми. Для того чтобы найти равнодействующую сил на втулке, удобно рассмотреть суммирование одноименных гармоник нагрузок, создаваемых на каждой из лопастей. При этом необходимо учесть направление действия нагрузок на разных лопастях. Нагрузку, приходящую с каждой лопасти, имеющей номер i, можно разложить по трем направлениям: по направлению оси винта - это векторы тяги и крутящего момента , а два других расположены в плоскости вращения перпендикулярно оси горизонтального шарнира и параллельно ей (перпендикулярно оси лопасти) . Векторы и от разных лопастей параллельны друг другу, а векторы и соседних лопастей повернуты относительно друг друга на угол , где K_л - число лопастей винта.

Для гармоник нагрузок, векторы которых параллельны оси вращения винта, применяется первое правило суммирования (Михеев Р.А. Прочность вертолетов. М.: Машиностроение, 1984, с.30). Согласно этому правилу гармоники с номерами и кратными числу лопастей:

и амплитудами нагрузок A_n различных лопастей складываются и дают на втулке равнодействующую, имеющую амплитуду и ту же частоту. Они без изменения амплитуд и частот гармонических составляющих сил передаются на фюзеляж. Такие гармоники называются проходными. Гармоники с номерами, некратными числу лопастей, т.е. не удовлетворяющие условию (1) ни при каком целом m и, на втулке взаимно уравновешиваются и не передаются на фюзеляж. Эти гармоники называются непроходными.

Для гармоник сил на втулке, находящихся в плоскости вращения винта и повернутых относительно друг друга на угол Δψ, равный углу между лопастями, применяется второе правило суммирования (Михеев Р.А. Прочность вертолетов. М.: Машиностроение, 1984. с.37).

В соответствии с этим правилом проходными являются гармоники с номерами, на единицу отличающимися от номеров, кратных числу лопастей:

и первая гармоника, которая соответствует значению m=0. Амплитуда этой нагрузки равна амплитуде гармоники одной лопасти, умноженной на половину числа лопастей. Это правило справедливо для винтов с числом лопастей К_л≥3.

При передаче этих гармоник в невращающуюся систему координат O_нX_нZ_н гармоники с номерами mК_л±1 трансформируются в лопастные гармоники

Однако эти правила относятся к классическим винтам, т.е. к таким винтам, у которых лопасти расположены по диску равномерно, что не позволяет конструктору при проектировании воздушных винтов управлять нагрузками и вибрациями, передающимися с винтов на конструкцию.

Известны рулевые винты Х-образного типа (схема «ножницы»), установленные на вертолетах АН-64А «Апач» (США), Ми-28 и Ми-38 (Россия).

В описании вертолета «Апач», составленном по материалам открытой иностранной печати (Боевой вертолет Макдоннел-Дуглас АН-64А «Апач» (по материалам открытой иностранной печати). ОНТИ ЦАГИ, 1989. с.23), приводятся сведения о том, что использование неравномерного расположения между парами лопастей (острый угол Х=55°) привело к уменьшению уровня четвертой гармоники составляющей шума.

В работе (Рождественский М.Г., Самохин В.Ф. Аэродинамические и акустические особенности винта схемы «ножницы». Аэродинамика. Статья в Трудах шестого Форума РосВО, 2004. с.I-103…I-117) показано, что компоновка винта схемы «ножницы» имеет преимущества по сравнению с характеристиками винта с ортогональным расположением лопастей: увеличение тяги достигает 7%, а максимальное увеличение коэффициента полезного действия составляет 10%.

Рулевой винт типа «фенестрон» с десятью лопастями, неравномерно расположенными по диску, реализован на вертолетах ЕС130 и ЕС135 фирмы Eurocopter (Журнал «Вертолетная индустрия», декабрь 2007, с.25). По данным фирмы на вертолете с винтом, выполненным по такой концепции, удалось существенно снизить уровень шума, потребную мощность и повысить аэродинамическое качество.

Известен патент РФ №1826421 Преобразуемый несущий винт преимущественно комбинированного ЛА, содержащий втулку винта, четыре лопасти с симметричным профилем, установленные под углом 90° для полета по-вертолетному, а для самолетного режима винт в плане становится Х-образным. В самолетном режиме консоли устанавливаются с меньшим углом стреловидности по отношению к набегающему потоку (угол стреловидности Х=30°), что позволяет улучшить несущие свойства системы «несущий винт-крыло».

Однако в данном патенте вопросы снижения уровней нагрузок и вибраций, действующих на конструкцию комбинированного ЛА, не рассматривались.

Технический результат, на достижение которого направлено изобретение, заключается в увеличении ресурса конструкции ЛА по условиям усталостной прочности путем снижения нагрузок и вибраций.

Для достижения названного технического результата в предлагаемом способе, включающем неравномерное расположение лопастей по диску, установленных попарно, с сохранением симметрии относительно ортогональных осей винта, согласно изобретению, комбинируют типы винтов с четным числом лопастей от четырех и более следующим образом:

4-лопастной (Х-образный) винт образуют из двух пар лопастей;

6-лопастной винт компонуют из Х-образного и двухлопастного винтов;

8-лопастные винты формируют: из двух 4-лопастных классических винтов; из Х-образного и 4-лопастного классического винтов; из двух Х-образных винтов;

10 - лопастной винт комбинируют из двух Х-образных и одного 2-хлопастного винтов.

Определяют математическую модель расчета гармонических составляющих векторов переменных нагрузок для каждой лопасти в зависимости от углов пар лопастей ΔΨ₁. Суммируют векторы нагрузок от каждой лопасти на втулке винта по трем осям OY₁, OX₁, OZ₁, вращающейся системы координат с началом в центре втулки винта ЛА, затем проектируют полученные векторы нагрузок на неподвижные оси координат ЛА O_нX_н, и O_нZ_н. Выполняют гармонический анализ проекций векторов нагрузок на продольную O_нX_н и поперечную O_нZ_н оси координат, строят зависимости амплитуд этих гармонических составляющих от углов ΔΨ₁, из них выбирают значения углов, соответствующих минимальному уровню гармоник переменных нагрузок.

Для 10-лопастного винта определяют аналитически методом последовательных приближений сочетания углов ΔΨ₁, ΔΨ₂, при которых нагрузки и вибрации, действующие на конструкцию ЛА, равны нулю, где ΔΨ₁ - угол между осями соседних пар лопастей, а ΔΨ₂ - угол между осями смежных пар лопастей. Выбранные углы используют при компоновке винта.

Таким образом, полученные значения углов ΔΨ₁ и ΔΨ₂, соответствующие минимальным и нулевым гармоническим составляющим, позволяют существенно снизить уровень нагрузок и вибраций, действующих на конструкцию ЛА.

Предлагаемый способ поясняется следующими фигурами:

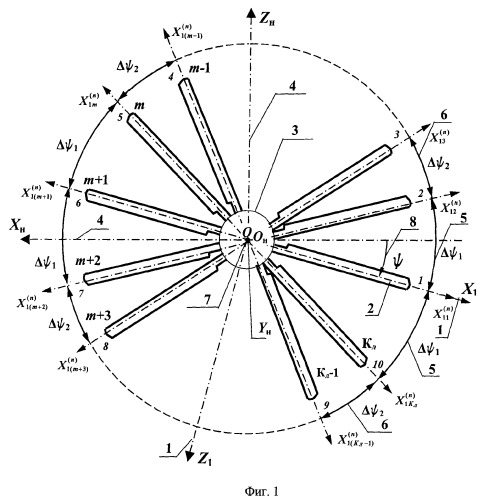
На фиг.1 показана схема многолопастного винта с неравномерным расположением лопастей по диску, где

1 - вращающиеся оси координат винта OX₁ и OZ₁;

2 - оси лопастей №1, 2, … К_л;

3 - втулка винта;

4 - оси О_нХ_н и О_нZ_н в неподвижной системе координат O_нХ_нZ_н;

5 - углы между соседними лопастями ΔΨ₁;

6 - углы между осями смежных лопастей ΔΨ₂;

7 - вертикальная ось координат О_нY_н;

8 - азимутальное положение Ψ оси лопасти №1.

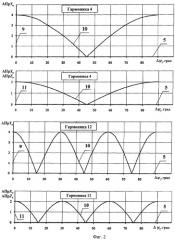
На фиг.2 показаны зависимости амплитуд проекций нагрузок 10 на неподвижные оси координат от углов ΔΨ₁ 5 для четвертой и двенадцатой гармоник, где

5 - углы между осями соседних лопастей ΔΨ₁;

9 - амплитуды проекций векторов нагрузок на вертикальную ось координат O_нY_н 7;

11 - амплитуды проекций векторов нагрузок на неподвижные оси координат 4: продольная О_нZ_н, поперечная O_нZ_н.

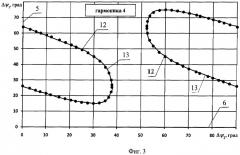
На фиг.3 приведены сочетания между углами ΔΨ₁ и ΔΨ₂, соответствующие нулевому уровню амплитуды четвертой гармоники, где

5 - углы между осями соседних лопастей ΔΨ₁;

6 - углы между осями смежных лопастей ΔΨ₂;

12 - точка, соответствующая нулевой четвертой гармонике, полученная расчетом;

13 - интерполяционный полином, соответствующий нулевому уровню нагрузок по четвертой гармонике.

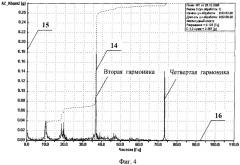
На фиг.4 приведен амплитудный спектр вибраций 14 на шпангоуте №2 килевой балки вертолета Ми-38 ОП-1, где

15 - амплитуды виброперегрузок (в единицах g) на килевой балке (КБ), шпангоут 2 (шп 2);

16 - частота колебаний, Гц.

Способ осуществляется следующим образом

В предлагаемом способе, включающем неравномерное расположение лопастей по диску, установленных попарно с сохранением симметрии относительно ортогональных осей винта, комбинируют типы винтов с четным числом лопастей от четырех и более следующим образом:

4-лопастной (Х-образный) винт образуют из двух пар лопастей;

6-лопастной винт компонуют из Х-образного и двухлопастного винтов;

8-лопастные винты формируют: из двух 4-лопастных классических винтов; из Х-образного и 4-лопастного классического винтов; из двух Х-образных винтов;

10-лопастной винт комбинируют из двух Х-образных и одного 2-хлопастного винтов.

Определяют математическую модель расчета гармонических составляющих векторов переменных нагрузок для каждой лопасти в зависимости от углов пар лопастей ΔΨ₁. Суммируют векторы нагрузок от каждой лопасти на втулке винта по трем осям OY₁, OX₁, OZ₁ вращающейся системы координат с началом в центре втулки винта ЛА, затем проектируют полученные векторы нагрузок на неподвижные оси координат ЛА O_нX_н и О_нZ_н. Выполняют гармонический анализ проекций векторов нагрузок на продольную О_нХ_н и поперечную O_нZ_н оси координат, строят зависимости амплитуд этих гармонических составляющих от углов ΔΨ₁, из них выбирают значения углов, соответствующих минимальному уровню гармоник переменных нагрузок.

Для 10-лопастного винта определяют аналитически методом последовательных приближений сочетания углов ΔΨ₁, ΔΨ₂, при которых нагрузки и вибрации, действующие на конструкцию ЛА, равны нулю, где ΔΨ₁ - угол между осями соседних пар лопастей, a ΔΨ₂ - угол между осями смежных пар лопастей. Выбранные углы используют при компоновке винта.

Таким образом, полученные значения углов ΔΨ₁ и ΔΨ₂, соответствующие минимальным и нулевым гармоническим составляющим, позволяют существенно снизить уровень нагрузок и вибраций, действующих на конструкцию ЛА.

Сущность изобретения поясняется схемой многолопастного винта, приведенной на фиг.1. Лопасти нумеруются (например, на вертолете) по мере прохождения их над хвостовой балкой (отрицательное направление оси O_нX_н 4 в неподвижной системе координат). При выборе вращающихся осей координат ОХ₁Z₁ ось OX₁ 1 направляется по оси лопасти №1. Ось OZ₁ 1 должна быть перпендикулярна оси OX₁ и опережать ее.

В неподвижной системе координат продольная ось O_нX_н 4 направлена вперед, а поперечная ось O_нZ_н 4 - вправо для несущего винта и вверх для рулевого винта.

Оси координат во вращающейся OY₁ и в невращающейся O_нY_н 7 системах координат направляются по оси вращения в направлении тяги винта (эти оси совпадают).

Рассмотрим изменение n-гармоник переменных нагрузок для каждой лопасти i в зависимости от азимутального положения 8 оси лопасти №1 и углов между лопастями ΔΨ₁ 5 и ΔΨ₂ 6 (обозначим последние два угла как ΔΨ_j):

Находим равнодействующую сил винта , приходящих на втулку винта от каждой лопасти, для каждой из гармоник n, количество лопастей К_л - произвольное и четное:

В результате сложения одноименных гармоник получаются зависимости равнодействующих нагрузок на периоде вращения винта при разных углах между парами лопастей Δψ₁ 5 и ψ₂ 6.

Путем аналитических выкладок и численных расчетов можно показать, что проходными гармониками нагрузок, векторы которых параллельны оси вращения винта, является ряд гармоник с четными номерами, т.е. n=2, 4, 6, ... N. Это правило авторы изобретения назвали «третьим правилом суммирования гармоник». Максимальный номер четной гармоники N устанавливается из опыта летных испытаний. Таким же способом можно доказать, что все нечетные гармоники рассматриваемых нагрузок являются непроходными.

Определим значения углов Δψ_j, при которых амплитуды гармоник будут минимальными. Для решения задачи минимизации нагрузок целесообразно считать, что лопасти винта идентичны по своим аэродинамическим, массовым и жесткостным характеристикам, а амплитуды разных гармоник на всех лопастях равны единичной нагрузке, т.е. .

По аналогии с (1) запишем выражения для гармоник в плоскости OX₁Z₁ каждой лопасти i на периоде вращения винта в зависимости от азимутального положения оси лопасти №1 с учетом углов между осями пар лопастей Δψ_j 5 и 6:

.

Проекции векторов нагрузок на вращающиеся оси координат будут равны и .

Начало координат О (например, для вертолета) расположим в центре втулки винта. Азимут вращающейся оси OX₁, т.е. ψ 8, будем отсчитывать от отрицательного направления оси O_нX_н 4. Тогда проекции гармоник нагрузок на неподвижные оси координат будут равны:

Рассмотрим четыре варианта исполнения комбинированных винтов: 4-лопастной, 6-лопастной, 8-лопастной (три варианта) и 10-лопастной. Углы между лопастями на первых трех винтах можно выразить с помощью одного угла Δψ₁ 5, а на 10-лопастном винте - двумя углами: между соседними лопастями Δψ₁ 5 и смежными Δψ₂ 6, т.е. следующими после соседних пар лопастей по вращению и против вращения винта, что наглядно иллюстрируется на фиг.1.

Приравняв сумму гармонических составляющих (2) и (3) для каждой из гармоник нулю, находим углы Δψ_j, соответствующие нулевым значениям амплитуд:

;

;

.

Выполним гармонический анализ функций и при разных значениях углов Δψ_j.

Авторами предлагаемого изобретения проведен расчет зависимостей амплитуд проекций нагрузок на три указанные выше оси координат от угла Δψ₁ для 4-, 6- и 8-лопастного винтов. При этом рассмотрены все четные гармоники в диапазоне n=2…32. Для 10-лопастного винта рассчитаны сочетания соседних Δψ₁ и смежных Δψ₂ углов, при которых четные гармоники в том же диапазоне номеров n=2…32 равны нулю.

Результаты расчетов поясняются графиками на фиг.2 и 3, на которых изображены:

фиг.2 - зависимости амплитуд проекций нагрузок 10 на вертикальную АПрY_н 9, продольную АПрX_н 10 и поперечную AПрZ_н 10 оси координат, 4-лопастной винт, гармоники четыре и двенадцать.

Из приведенных данных на фиг.2 следует, что максимальные значения амплитуд проекций нагрузок равны: на вертикальную ось - сумме сил отдельных лопастей (в нашем случае - числу лопастей винта), а амплитуды проекций на продольную и поперечную оси равны половине числа лопастей. На графиках фиг.2 видно, что большие диапазоны занимают углы Δψ₁, при которых амплитуды нагрузок меньше, чем на классических винтах.

Сочетания углов между соседними Δψ₁ 5 и смежными Δψ₂ 6 лопастями на 10-лопастном воздушном винте приведены на фиг.3 (четвертая гармоника). Видно, что зависимости между углами Δψ₁ и Δψ₂ имеют эллипсовидный характер. Точки 12 на графиках получены расчетным путем. При анализе результатов расчета следует иметь в виду, что указанные зависимости представляют из себя кривые 13, проведенные по точкам. Число сочетаний углов Δψ₁ и Δψ₂ является бесконечно большим и оно увеличивается по мере увеличения номера гармоники n. Таким образом, при проектировании 10-лопастного винта имеются большие возможности для снижения или обнуления целого ряда гармонических составляющих переменных нагрузок.

Пример.

На фиг.4 приведен амплитудный спектр вибраций 14 на шпангоуте №2 килевой балки вертолета Ми-38 ОП-1, где

15 - амплитуды виброперегрузок (в единицах g) на килевой балке (КБ), шпангоут 2 (шп 2);

16 - частота колебаний, Гц.

На вертолете Ми-38 установлен 4-лопастной Х-образный рулевой винт с углом между осями лопастей Δψ₁=38°.

Из приведенной зависимости следует подтверждение основных положений предлагаемого изобретения. Так, в амплитудном спектре виброперегрузок, определяемых нагрузками на Х-образном рулевом винте, отмечается вторая гармоника, которая отсутствует на классическом 4-лопастном винте. Четвертая гармоника амплитудного спектра (фиг.4), которая является проходной лопастной на классическом винте, в данном случае значительна по величине. Предлагаемым авторами способом она могла бы быть снижена практически до нуля. Для этого необходимо, чтобы углы между осями лопастей были равны Δψ₁=45°. Это наглядно иллюстрируется зависимостью 10 амплитуд четвертой гармоники от углов между соседними лопастями Δψ₁ 5 (фиг.2), из которой видно, что при Δψ₁=45° амплитуды проекций векторов нагрузок 9, 11 на все три оси неподвижной системы координат равны нулю.

Практическое значение предлагаемого способа заключается в том, что он позволяет создавать воздушные винты, у которых любая гармоника или целый ряд гармоник нагрузок и вибраций, передающихся с воздушного винта на конструкцию летательного аппарата, может быть уменьшена до нуля или сведена до минимума. В частности, в вертолетостроении актуальной является проблема обеспечения усталостной прочности валов несущих и рулевых винтов, главных, хвостовых и промежуточных редукторов, подредукторных рам, средних и хвостовых частей фюзеляжа, килевых (концевых) балок.

Использование изобретения позволит уменьшить уровень нагруженности и вибраций в указанных частях конструкции и существенно повысить их ресурс по условиям усталостной прочности.

Известно (см. Богданов Ю.С. и др. Конструкция вертолетов. М.: Машиностроение, 1990. с.70), что даже небольшое изменение амплитуды переменных нагрузок (напряжений Δσ) приводит к существенному изменению ресурса конструкции. Так, при уменьшении Δσ на 10% ресурс увеличивается в 1,5…2 раза. В нашем случае отмечаются большие диапазоны углов Δψ₁, в которых амплитуды нагрузок значительно меньше, чем на классических винтах. Поэтому имеет существенное значение не только обнуление гармоник, но и их уменьшение по сравнению с нагрузками на классических винтах.

При летных испытаниях вертолетов Ми-28 и Ми-38, имеющих Х-образные рулевые винты, выявлено, что в записях вибраций, передающихся на хвостовую часть фюзеляжа, отмечены четные гармоники, начиная со второй. Предложенный способ легко объясняет появление таких «непривычных» для специалистов гармоник. Поэтому предложенное изобретение может быть использовано также при анализе результатов летных прочностных испытаний вертолетов, самолетов и автожиров с воздушными винтами, выполненными по предлагаемой концепции.

Способ уменьшения нагрузок и вибраций на летательных аппаратах, имеющих многолопастные воздушные винты с четным числом лопастей, включающий неравномерное расположение лопастей по диску, устанавливаемых попарно с сохранением симметрии относительно ортогональных осей винта, отличающийся тем, что комбинируют типы винтов с четным числом лопастей от четырех и более, определяют математическую модель расчета гармонических составляющих векторов переменных нагрузок для каждой лопасти в зависимости от углов между осями соседних пар лопастей ΔΨ₁, суммируют векторы нагрузок от каждой лопасти на втулке винта по трем осям OY₁, ОХ₁, OZ₁ вращающейся системы координат с началом в центре втулки винта летательного аппарата, а затем проектируют полученные векторы нагрузок на неподвижные оси координат летательного аппарата О_нХ_н и O_нZ_н, выполняют гармонический анализ проекций векторов нагрузок на продольную О_нХ_н и поперечную O_нZ_н оси координат, строят зависимости амплитуд этих гармонических составляющие от углов ΔΨ₁, из них выбирают значения расчетных углов, соответствующие минимальному уровню гармоник переменных нагрузок, а для 10-лопастного винта определяют аналитически методом последовательных приближений сочетания углов ΔΨ₁, ΔΨ₂, при которых нагрузки и вибрации, действующие на конструкцию летательного аппарата, равны нулю, где ΔΨ₁ - угол между осями соседних пар лопастей, а ΔΨ₂ - угол между осями смежных пар лопастей, производят компоновку винтов на летательном аппарате в соответствии с выбранными расчетными углами между осями пар лопастей.

2. Способ уменьшения нагрузок и вибраций на летательном аппарате, имеющих многолопастные воздушные винты с четным числом лопастей по п.1, отличающийся тем, что комбинируют типы винтов с четным числом лопастей от четырех и более следующим образом: 4-лопастной (Х-образный) винт образуют из двух пар лопастей; 6-лопастной винт компонуют из Х-образного и двухлопастного винтов; 8-лопастные винты формируют из двух 4-лопастных классических винтов из Х-образного и 4-лопастного классического винтов или из двух Х-образных; 10-лопастной винт комбинируют из двух Х-образных и одного 2-лопастного винтов.