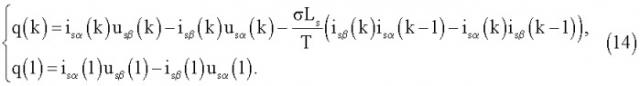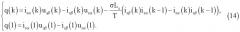Способ оптимальной оценки частоты вращения асинхронного двигателя и система для его реализации

Способ оптимальной оценки частоты вращения асинхронного двигателя и система для его реализации

Иллюстрации

Показать все

Реферат

Изобретение относится к области автоматического управления сложными объектами, а именно к системам управления электроприводами с наблюдателями состояния, и может быть использовано для оптимального цифрового управления асинхронными двигателями.

Известен способ косвенного вычисления частоты вращения асинхронного двигателя, реализованного в электроприводе переменного тока (а.с. СССР №1758821, МПК Н02Р 5/28, опубл. 30.08.92) и в устройстве для регулирования частоты вращения трехфазного асинхронного двигателя (а.с. СССР №1679596, МПК Н02Р 5/36, опубл. 23.09.91). Суть оценки частоты вращения асинхронного двигателя заключается в измерении действующих значений тока и напряжения статора двигателя и определении частоты вращения двигателя на основе параметров его схемы замещения.

Недостатком способа является невысокая точность в определении частоты вращения двигателя, обусловленная существенным отличием параметров модели двигателя, полученных на основе действующих значений тока и напряжений, от параметров реального двигателя и вследствие наличия широкого спектра помех при измерении текущих значений токов и напряжений. Поэтому такой способ практически невозможно реализовать в электроприводах и устройствах управления двигателем, удаленных на значительное расстояние от источника питания.

Наиболее близким по технической сущности и достигаемому результату является способ оценки частоты вращения асинхронного двигателя (Digital Motor Control Software Library (Rev. A) Digital Motor Control Software Library Digital Control Systems (DCS) Group SPRU485A August 2001 Revised October 2003 IMPORTANT NOTICE Texas Instruments Incorporated and … - http://focus-webapps.ti.com/general/docs/sitesearch/searchsite.tsp;jsessionid=HWTNYU2L5GZGBQC1JAVSM4Q?selectedTopic=1653260327&numRecords=25&searchTerm=aci_mras&statusCode=null), осуществляемый путем измерения текущих значений напряжений и токов статора двигателя, прямого и косвенного вычисления значений реактивной мощности, пропорционально-интегрального преобразования разности этих значений в оценку частоты вращения двигателя.

Недостатком такого способа является невысокая точность оценки частоты вращения двигателя вследствие неоптимального выбора значений параметров пропорционально-интегрального преобразования разности значений прямого и косвенного вычислений реактивной мощности двигателя.

Система, реализующая этот способ оптимальной оценки частоты вращения асинхронного двигателя, содержит блоки прямого и косвенного вычисления реактивной мощности, выходы которых соединены со входами блока сравнения, подключенного к входу блока вычисления оценки, выход которого соединен со вторым входом блока косвенного вычисления реактивной мощности.

Недостатком данной системы является плохая сходимость оценки частоты вращения вследствие неоптимального выбора параметров блока вычисления оценки.

Задачей изобретения является повышение точности оценки частоты вращения асинхронного двигателя.

Поставленная задача решается тем, что оценка частоты вращения асинхронного двигателя, так же как в прототипе, осуществляется путем измерения текущих значений напряжений и токов статора двигателя, прямого и косвенного вычисления значений реактивной мощности, пропорционально-интегрального преобразования разности этих значений в оценку частоты вращения двигателя.

Новым является то, что предложенный способ оптимальной оценки частоты вращения асинхронного двигателя обеспечивает расчет параметров пропорционально-интегрального преобразования на основе минимизации критерия качества, определяемого по сохраненным ранее двум предыдущим значениям оценки частоты вращения и разности значений прямого и косвенного вычислений реактивной мощности, а в систему для реализации способа оптимальной оценки частоты вращения асинхронного двигателя введены блок измерения, соединенный через блок преобразования координат с блоками прямого и косвенного вычисления реактивной мощности, блок оптимизации параметров оценки, выход которого соединен со вторым входом блока вычисления оценки, первый блок задержки, вход которого соединен с выходом блока сравнения и первым входом блока оптимизации параметров оценки, а выход - со вторым входом блока оптимизации параметров оценки, второй блок задержки, вход которого соединен с выходом блока вычисления оценки и третьим входом блока оптимизации параметров оценки, а выход подключен к четвертому входу блока оптимизации параметров оценки и третьему входу блока вычисления оценки.

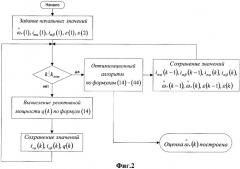
Изобретение поясняется чертежами, где на фиг.1 представлена блок-схема алгоритма вычисления оценки реактивной мощности методом Рунге-Кутта, на фиг.2 - блок-схема алгоритма построения оценки частоты вращения асинхронного двигателя, на фиг.3 - функциональная схема системы оптимальной оценки частоты вращения асинхронного двигателя.

Способ оптимальной оценки частоты вращения асинхронного двигателя включает в себя следующие действия.

Измеряются текущие значения фазных токов i_sa(t), i_sb(t), i_sc(t) и напряжений u_sa(t), u_sb(t), u_sc(t) статора двигателя, значения которых преобразуются из симметричной трехфазной системы координат в двухфазную неподвижную систему координат {α, β}:

, , ,

где i_sα(t), i_sβ(t), u_sα(t), u_sβ(t) - составляющие векторов тока и напряжения статора, представленные в двухфазной неподвижной системе координат.

На основе значений i_sα(t), i_sβ(t), u_sα(t), u_sβ(t) вычисляются мгновенные значения противо-эдс e_sα(t), e_sβ(t) в статорной обмотке асинхронного электродвигателя:

где L_m - взаимная индуктивность ротора и статора;

L_r - индуктивность ротора;

L_s - индуктивность статора;

Ψ_rα(t), Ψ_rβ(t) - потокосцепление ротора по осям α и β соответственно; R_s - сопротивление статора;

- коэффициент рассеивания двигателя.

Определяется реактивная мощность q(t) при прямом вычислении на основе векторного произведения вектора токов и вектора противо-эдс статора двигателя (с учетом равенства нулю векторного произведения токов статора :

В результате представления вектора противо-эдс статора в неподвижной системе координат {α, β}

где j - мнимая единица,

окончательно определяется реактивная мощность q(t):

Определяется реактивная мощность по косвенному алгоритму с использованием значений токов i_sα(t), i_sβ(t) статора в неподвижной системе координат {α, β} и оценки частоты вращения двигателя. Вычисляются оценки противо-эдс статора и которые в неподвижной системе координат {α, β} записываются следующим образом:

где символ ^ - означает оценку соответствующих переменных;

- постоянная времени ротора;

R_r - активное сопротивление ротора;

i_mα(t) и i_mβ(t) - соответственно токи намагничивания по осям α и β в неподвижной системе координат.

Рассчитываются значения токов намагничивания i_mα(t) и i_mβ(t) в результате решения следующей системы дифференциальных уравнений:

Вычисляется оценка реактивной мощности на основе векторного произведения:

Для реализации алгоритмов вычисления значений реактивной мощности q(t) и в цифровом виде дифференциальные уравнения (5) и (11) записываются в дискретной форме на интервалах времени (kT),

где k=1, 2, …; Т - период дискретизации вычислений.

Используя разностную аппроксимацию уравнения (5) для (k)-го вычислительного шага, получим выражение:

Для первого (начального) вычислительного шага значение реактивной мощности q(k=1) определяется уравнением:

После преобразования уравнения (12) получим итоговый алгоритм прямого расчета реактивной мощности q(k) в форме дискретных уравнений:

Используя уравнение (10), записывается дискретное выражение для оценки реактивной мощности:

где оценка противо-эдс статора двигателя по осям α и β в неподвижной системе координат вычисляется следующим образом:

Для цифрового вычисления значений токов i_mα(k) и i_mβ(k) по дифференциальным уравнениям (9), (10) используется метод Рунге-Кутта четвертого порядка. Блок-схема алгоритма вычисления i_mα(k) и i_mβ(k) приведена на фиг.1. В этом случае дискретные значения i_mα(k) и i_mβ(k) могут быть рекуррентно получены следующим образом:

где коэффициенты K_i и L_i, вычисляются по уравнениям:

где функции и определяются выражениями:

При равенстве значений фазных токов i_sa (t), i_sb (t), i_sc(t) и реальной частоты ω_r(t) вращения ротора двигателя нулю ω_r(t)=0, значения токов i_mα(k=1), i_mβ(k=1), i_mα(k=2), i_mβ(k=2) на первых двух интервалах дискретности моделирования вычисляются на основе следующих соотношении:

где коэффициенты K2_i и L2_i при изменении определяются уравнениями:

Вычисление оценки частоты вращения двигателя осуществляется на основе пропорционально-интегрального закона, который в дискретной форме записывается в виде:

где К_Р, K_I - соответственно коэффициенты пропорциональной и интегральной составляющих закона;

ε(k) - разница значений прямого q(k) и косвенного вычислений реактивной мощности:

Преобразуя уравнение (40) к разностному виду, оценка частоты вращения двигателя вычисляется по формуле:

где С - положительный нормирующий коэффициент.

Для определения коэффициентов К_Р, K_I пропорционально-интегрального закона (40) используется следующая процедура: по ранее сохраненным данным за определенный промежуток времени Т_ОПТ=k_ОПТТ,

где k_ОПТ - целое положительное число, вычисляется функция качества:

Оптимальными будут считаться такие значения коэффициентов К_Р, K_I, при которых функция качества S(K_P, K_I, k) принимает минимальное значение:

При определении оценки частоты вращения двигателя (фиг.2) предполагается задание начальных условий, которые обеспечиваются на первом и втором интервалах вычислений равенствами: i_mα(k=1)=0, i_mβ(k=1)=0, ε(k=1)=0, ε(k=2)=q(k=1).

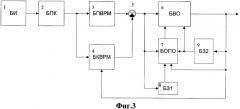
На фиг.3 приведена функциональная схема системы оптимальной оценки частоты вращения асинхронного двигателя, реализующей способ оптимальной оценки частоты вращения асинхронного двигателя.

Система оптимальной оценки частоты вращения асинхронного двигателя содержит блок 1 измерения (БИ), блок 2 преобразования координат (БПК), блоки прямого 3 (БПВРМ) и косвенного 4 вычисления (БКВРМ) реактивной мощности, блок 5 сравнения, блок 6 вычисления оценки (БВО), блок 7 оптимизации параметров оценки (БОПО), первый блок 8 задержки (БЗ1), второй блок 9 задержки (БЗ2).

Блок 1 измерения (БИ) соединен через блок 2 преобразования координат (БПК) с блоками прямого 3 (БПВРМ) и косвенного 4 вычисления (БКВРМ) реактивной мощности, блок 7 оптимизации параметров оценки (БОПО), выход которого соединен со вторым входом блока 6 вычисления оценки (БВО), первый блок 8 задержки (БЗ1), вход которого соединен с выходом блока 5 сравнения и первым входом блока 7 оптимизации параметров оценки (БОПО), а выход - со вторым входом блока 7 оптимизации параметров оценки (БОПО), второй блок 9 задержки (БЗ2), вход которого соединен с выходом блока 6 вычисления оценки (БВО) и третьим входом блока 7 оптимизации параметров оценки (БОПО), а выход подключен к четвертому входу блока 7 оптимизации параметров оценки (БОПО) и третьему входу блока 6 вычисления оценки (БВО).

Техническое исполнение блоков системы оптимальной оценки частоты вращения асинхронного двигателя может быть выполнено, например, на вычислительных и программных средствах программируемого логического контроллера ЭЛСИ-ТМ компании «ЭлеСи» (г.Томск).

Заявляемая система работает следующим образом.

После включения питающего напряжения системы устанавливаются начальные значения: i_mα(k=1)=0, i_mβ(k=1)=0, ε(k=1)=0, ε(k=2)=q(k=1).

В рабочем режиме блок 1 измерения (БИ) осуществляет дискретное измерение фазных токов i_sa (k), i_sb (k), i_sc(k) и напряжений u_sa (k), u_sb (k), u_sc(k) асинхронного двигателя. Блок 2 преобразования координат (БПК) выполняет преобразование измеренных мгновенных значений фазных токов и напряжений из симметричной трехфазной системы координат в двухфазную неподвижную систему координат {α, β}.

Реактивная мощность асинхронного двигателя одновременно вычисляется двумя блоками: блоком 3 прямого (БПВРМ) и блоком 4 косвенного вычисления (БКВРМ) реактивной мощности. Значения реактивной мощности q(k) с выхода блока 3 (БПВРМ) и значения с выхода блока 4 (БКВРМ) сравниваются блоком 5 сравнения. Результаты сравнения ε(k) поступают в блок 6 вычисления оценки (БВО), блок 7 оптимизации параметров оценки (БОПО) и первый блок 8 задержки (БЗ1),

где С выхода первого блока 8 задержки (БЗ1) задержанный сигнал ε(k-1) поступает на второй вход блока 7 оптимизации параметров оценки (БОПО). Вычисленные в блоке 7 оптимизации параметров оценки (БОПО) значения коэффициентов пропорциональной К_Р и интегральной K_I составляющих закона (41) преобразования ошибки ε(k) в оценку частоты вращения поступают на второй вход блока 6 вычисления оценки (БВО). Коэффициенты К_Р, K_I вычисляются таким образом, чтобы текущая ошибка ε(k) стремилась к определенному заданному ε_ЗАД значению:

Рассчитанные в блоке 6 вычисления оценки (БВО) значения оценки частоты вращения поступают на третий вход блока 7 оптимизации параметров оценки (БОПО) и второй вход блока 4 косвенного вычисления (БКВРМ) реактивной мощности. С задержкой на один вычислительный такт значения оценки частоты вращения через второй блок 9 задержки (БЗ2) поступают на четвертый вход блока 7 оптимизации параметров оценки (БОПО) и третий вход блока 6 вычисления оценки (БВО) значения оценки частоты вращения.

В результате того, что коэффициенты К_Р, K_I пропорционально-интегрального закона преобразования ошибки ε(k) вычисляются оптимальным образом, повышается точность оценки частоты вращения асинхронного двигателя. Цифровая система, реализующая оптимальный способ оценки частоты вращения, позволяет получить значения ε(k) в реальном времени.

1. Способ оптимальной оценки частоты вращения асинхронного двигателя, включающий измерение текущих значений напряжений и токов статора двигателя, прямое и косвенное вычисление значений реактивной мощности, пропорционально-интегральное преобразование разности этих значений в оценку частоты вращения двигателя, отличающийся тем, что параметры пропорционально-интегрального преобразования вычисляются на основе минимизации критерия, определяемого по сохраненным в памяти двум предыдущим значениям оценки частоты вращения и разности значений прямого и косвенного вычислений реактивной мощности.

2. Система оптимальной оценки частоты вращения асинхронного двигателя, содержащая блоки прямого и косвенного вычисления реактивной мощности, выходы которых соединены со входами блока сравнения, подключенного к входу блока вычисления оценки, выход которого соединен со вторым входом блока косвенного вычисления реактивной мощности, отличающаяся тем, что введены блок измерения, блок оптимизации параметров оценки, выход которого соединен со вторым входом блока вычисления оценки, первый блок задержки, вход которого соединен с выходом блока сравнения и первым входом блока оптимизации параметров оценки, а выход - со вторым входом блока оптимизации параметров оценки, второй блок задержки, вход которого соединен с выходом блока вычисления оценки и третьим входом блока оптимизации параметров оценки, а выход подключен к четвертому входу блока оптимизации параметров оценки и третьему входу блока вычисления оценки.

3. Система оптимальной оценки частоты вращения асинхронного двигателя по п.2, отличающаяся тем, что блок измерения соединен с блоками прямого и косвенного вычисления реактивной мощности через блок преобразования координат.