Способ определения структуры и демодуляции сигнала с неизвестной структурой

Способ определения структуры и демодуляции сигнала с неизвестной структурой

Иллюстрации

Показать все

Реферат

Изобретение относится к радиотехнике и может быть использовано для целей радиоконтроля, согласованной фильтрации преднамеренных помех, скрытого определения характеристик источников радиоизлучения и для демодуляции сигнала с неизвестной структурой.

В настоящее время известны различные способы (см. патенты Российской Федерации №№ 2321018, 2236693, 2216748) распознавания сигналов с неизвестными параметрами. Предлагаемые способы используют классические методы обработки сигналов, основанные на преобразовании Фурье, вычислении автокорреляционной функции, огибающей, рассмотрении различных деревьев классификации.

Известен способ обнаружения импульсных сигналов с неизвестными параметрами. Заявленное изобретение относится к пассивной локации сигналов и включает преобразование входного сигнала в спектральное представление Фурье, вычисление квадрата модуля от спектрального представления входного сигнала, обратное преобразование Фурье, возведение модуля получаемой автокорреляционной функции в z-ю степень и интегрирование с последующей нормировкой результата интегрирования к максимуму модуля автокорреляционной функции в z-й степени, сравнение получаемого результата с порогом и вынесение соответствующего решения о наличии обнаруживаемого объекта. Достигаемым техническим результатом является малая чувствительность к формам обнаруживаемых импульсных сигналов и стабилизация вероятности ложной тревоги [Патент RU 2321018 C1, G01S 7/28, СПОСОБ ОБНАРУЖЕНИЯ ИМПУЛЬСНЫХ СИГНАЛОВ С НЕИЗВЕСТНЫМИ ПАРАМЕТРАМИ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ, опубликованный 27.03.2008].

Недостатком данного способа является возможность обнаружения только импульсных сигналов с неизвестными параметрами. При этом не решается общий случай обнаружения любого типа сигнала с неизвестной структурой.

Также известен способ распознавания вида и параметров модуляции радиосигналов на основе совместного использования методов спектрального и кластерного анализа. В предлагаемом способе сначала решается задача обнаружения многокомпонентного радиосигнала и его частотных компонент в полосе анализа. Затем выделяются частотные компоненты и находятся их огибающие. Вычисляя нормировочный коэффициент взаимной корреляции полученных огибающих частотных составляющих многокомпонентного сигнала и сравнивая его с порогом, принимается решение об отнесении принятого радиосигнала к классу сигналов с частотной манипуляцией [Патент RU 2236693 C1, G01S 13/52, G06K 9/00, СПОСОБ РАСПОЗНАВАНИЯ ЧАСТОТНО-МАНИПУЛИРОВАННЫХ СИГНАЛОВ С НЕИЗВЕСТНЫМИ ПАРАМЕТРАМИ, опубликованный 20.09.2004].

Недостатком данного способа является возможность распознавания параметров только частотно-манипулированных сигналов. При этом не решается общий случай определения параметров сигнала с неизвестной структурой и произвольным типом модуляции.

Анализ источников информации - патентной и научно-технической литературы показал, что наиболее близким является способ распознавания сигналов систем радиосвязи при заранее неизвестных параметрах принимаемого сигнала, основанный на многоступенчатой настройке параметров системы при приеме и цифровой обработке, включающей подстройку по частоте и полосе приема сигнала, изменение частоты дискретизации принятого сигнала, формирование контекстного второго набора классификационных признаков, а также адаптивное (контекстное) подключение второй половины дерева классификации [Патент RU 2216748 С2, G01R 23/16, СПОСОБ РАСПОЗНАВАНИЯ СИГНАЛОВ СИСТЕМ РАДИОСВЯЗИ, опубликованный 20.11.2003], который выбран в качестве прототипа.

Тем не менее указанный способ позволяет проводить адаптивное распознавание сигналов с неизвестной структурой в пределах ограниченного класса сигналов, определенных в классификационном дереве признаков, если же сигнал не определен в дереве классификации, то процедура обработки продолжается определенное число раз, после чего сигнал признается нераспознанным.

В работе [Патент RU 2216748 С2, G01R 23/16. СПОСОБ РАСПОЗНАВАНИЯ СИГНАЛОВ СИСТЕМ РАДИОСВЯЗИ, опубликованный 20.11.2003] предлагается способ распознавания сигналов, основанный на быстром преобразовании Фурье, данный подход имеет ряд недостатков, не позволяющих определять параметры сложного сигнала.

В предлагаемом способе для определения характеристик и демодуляции обработку сигнала производят в два этапа. При первичной обработке исследуют комплексные характеристики сигнала на основе вейвлет-анализа. К примеру, если считать, что каждый вейвлет имеет определенную "ширину" своего временного окна, которому соответствует определенная "средняя" частота Фурье-образа вейвлета, обратная его масштабному коэффициенту, то семейства масштабных коэффициентов вейвлет-преобразования можно считать аналогичными семействам частотных спектров оконного преобразования Фурье, но с одним принципиальным отличием. Масштабные коэффициенты действуют во времени, изменяя "ширину" вейвлетов и соответственно "среднюю" частоту их Фурье-образов, а следовательно, каждой частоте соответствует своя длительность временного окна анализа, и наоборот. Многоразмерное временное окно вейвлет-преобразования позволяет одинаково хорошо выявлять и низкочастотные, и высокочастотные характеристики сигналов.

Непрерывное вейвлет-преобразование (ВП) сигнала определяют выражением:

где - непрерывное вейвлет-преобразование сигнала,

S(t) - входной сигнал,

- масштаб вейвлет-функции,

t - текущее значение времени,

τ - сдвиг вейвлет-функции по оси времени,

Ψ(t) - является материнским вейвлетом,

Ψa(t) - дочерние вейвлеты, образованные масштабированием и сдвигом материнского вейвлета.

* - обозначает комплексное сопряжение.

Простейшим базисным вейвлетом является вейвлет Хаара

вейвлет-преобразование с использованием базиса Хаара обозначается (Haar WaveletTransform). В отличие от преобразования Фурье, базис ВП хорошо локализован как в частотной, так и во временной областях, что позволяет анализировать кратковременные особенности сигналов. Такими особенностями для сигналов цифровых систем связи являются переходные процессы в тактовые моменты времени. Если вейвлет полностью укладывается на тактовый интервал, то модуль ВП Хаара для сигналов с различными видами модуляции описывается выражениями:

где s, s_i - мощность элементарной посылки,

ω_н - несущая частота,

ω_i - частота элементарной посылки для ЧМ.

|HWT(τ)| - модуль ВП Хаара при фиксированном масштабе a в пределах тактового интервала зависит от амплитуды и частоты элементарной посылки. В тактовые моменты времени |HWT(τ)| имеет локальный минимум или максимум (из-за смены передаваемого символа). Таким образом, |HWT(τ)| ФМ сигнала представляет собой постоянную функцию (со всплесками соответствующими тактовым моментам времени), а ЧМ и КАМ сигналов - ступенчатые функции. Так как дисперсия постоянной функции много меньше дисперсии ступенчатой функции, то, устранив всплески путем фильтрации и рассчитав дисперсию |HWT(τ)| анализируемого сигнала, можно выделять сигналы с фазовой манипуляцией (ФМ).

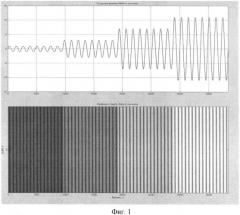
Рассмотрим амплитудно-манипулированный сигнал с четырьмя различными манипуляциями амплитуды (см. фиг.1 сверху). Построим его вейвлет-спектр и рассмотрим его особенности (см. фиг.1 снизу). Сравнивая между собой два рисунка, можно сделать вывод, что по вейвлет-спектру сигнала можно легко определить время скачка амплитуды и ее величину по интенсивности вертикальных полос.

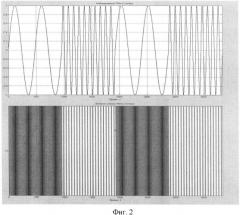
Рассмотрим частотно-манипулированный сигнал с двумя различными манипуляциями частоты (см. фиг.2 сверху). Построим его вейвлет-спектр (см. фиг.2 снизу) и рассмотрим его особенности. Сравнивая осциллограмму ЧМн сигнала и его вейвлет-спектр, можно сделать вывод о том, что в соответствующие моменты времени, в которые происходят манипуляции частоты, резко меняется интенсивность цвета и ширина вертикальных полос, что свидетельствует о скачке частоты. Фиксируя моменты изменения интенсивности вертикальных полос, определяется скорость передачи.

Распознавание и демодуляцию сигнала с неизвестной структурой осуществляют по средствам применения двухуровневой обработки сигнала, включающей первичную вейвлет-обработку и вторичный анализ в нейронных сетях. Поставленную задачу решают за счет того, вейвлет-обработка позволяет провести грубую оценку параметров сигнала (максимальная, минимальная амплитуда и частота), присутствие фазовых искажений. Вторичная обработка в нейронной сети позволяет точно определить параметры сигнала, при этом точность определения параметров сопоставима с уровнем шума. По результатам вторичной обработки корректируют структуру нейронной сети под данный тип сигнала, что существенно сокращает математические затраты на вычисление.

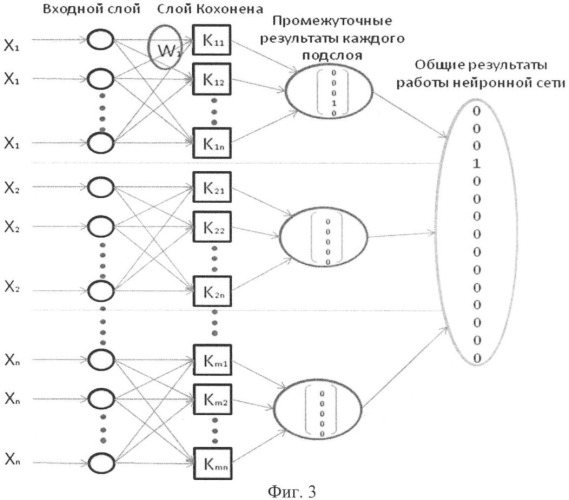
По результатам грубой первичной обработки сигнала формируют выходные данные для последующей детальной обработки. Эти данные содержат информацию о максимальной и минимальной амплитудах сигнала, наибольшей и наименьшей частотах входного сигнала. Также при рассматриваемом виде первичной обработки можно определить общее количество амплитуд, частот и фаз принимаемого сигнала. Поскольку определяемые параметры имеют точную привязку ко времени, то это позволяет определить информативность сигнала. Для этапа вторичной обработки предлагается использовать нейронную сеть с одним слоем Кохонена. Общий вид нейронной сети приведен на фиг.3.

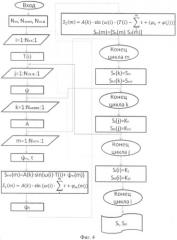
Алгоритм формирования данных для составных нейронов слоя Кохонена приведен на фиг 4. Входными параметрами являются количество присутствующих частот N_кч, количество амплитуд N_ампл и количество фазовых скачков во входном сигнале N_ск.ф. В соответствии с этими данными формируют циклы: первый цикл i соответствует числу частот, второй цикл j соответствует числу определяемых фаз, третий цикл k соответствует числу определяемых амплитуд и четвертый цикл m соответствует числу оцифровок, проведенных АЦП за период (см. фиг.4). Таким образом, общая картина формирования данных для нейронов слоя Кохонена следующая: для данного значения частоты, фазы и амплитуды вычисляется m гармоник с длительностью в один период и с разной начальной фазой, то есть данный скачок фазы входного сигнала как бы перемещают в разные точки периода, что позволяет проводить обработку сигнала без начальной синхронизации. На выходе формируют два вектора S_i (вектор с различными фазовыми скачками) и S_io (просто гармонический сигнал с различными частотами и амплитудами).

Ассоциированное с каждым нейроном Кохонена множество весов соединяет его с каждым входом. Например, на фиг.1 нейрон Кохонена К₁ имеет веса w₁₁, w₂₁,…, w_m1, составляющие весовой вектор W₁. Они соединяются через входной слой с входными сигналами х₁, х₂,… х_m, составляющими входной вектор X. Подобно нейронам большинства сетей выход NET каждого нейрона Кохонена является просто суммой взвешенных входов. Это может быть выражено следующим образом:

NET_j=w_1j·x₁+w_2j·х₂+…+w_mj·х_2m,

где NET_j - это выход NET нейрона Кохонена j,

NET_j=∑_ix_i·w_ij

или в векторной записи

N=X·W,

где N - вектор выходов NET слоя Кохонена. Нейрон Кохонена с максимальным значением NET является «победителем». Его выход равен единице, у остальных он равен нулю.

Весовой вектор W является цифровым представлением сигнала с единичным периодом, формирование которого изображено на фиг.4. В зависимости от заданной точности обработки сигнала и результатов первичной обработки сигнала формируется набор базовых векторов, которые впоследствии становятся весами нейронов. Число нейронов К_n выбирается в зависимости от набора базовых векторов с единичным периодом и необходимой точности определения параметров сигнала.

Каждому нейрону К_n соответствует весовой вектор W_n. Сеть Кохонена на выходе каждого подслоя формирует выходной вектор с одним "выигравшим" нейроном, соответствующий наибольшему подобию входного сигнала. При этом если в одной подсети появился такой нейрон, то во всех остальных подсетях на выходе будут нули. Таким образом, на выходе нейронной сети мы получим предельно точные характеристики сигнала на данном отрезке времени.

При этом с каждым нейроном Кохонена в одной подсети слоя Кохонена (см. фиг.3) ассоциируется один входной вектор, поэтому обучение синтезированного слоя Кохонена производят с помощью одного вычисления на вес, что существенно упрощает математическую процедуру вычислений. Диапазон изменения весов каждого нейрона определяется шумовыми составляющими входного сигнала. Таким образом, нейрон распознает входной сигнал в пределах "размытости" его весов. Организованная таким образом обработка дает возможность определить точные значения параметров сигнала, при этом точность определения параметров ограничена уровнем шума входного сигнала.

По окончании вторичной обработки нейронную сеть модифицируют таким образом, чтобы остались только те нейроны, которые активировались в ходе вторичной обработки. После перестройки нейронной сети количество вычислений резко сокращается, поскольку сеть адаптируется под принимаемый сигнал.

Предложенный алгоритм двухэтапной обработки сигнала с неизвестной структурой является универсальным, поскольку позволяет системе автоматически подстраиваться под входной сигнал.

Достигаемым техническим результатом являются определение параметров и демодуляция сигнала с неизвестной структурой на основе самообучающейся нейронной сети, при этом точность обработки ограничена шумовыми составляющими входного сигнала.

Определив параметры, которыми модулирован сигнал, строится созвездие сигнала. Зная созвездие сигнала можно подобрать стандартный демодулятор или синтезировать адаптивный, учитывающий тонкую структуру сигнала, после чего осуществить его демодуляцию. Изложенный подход является уникальным, так как позволяет работать с сигналом, параметры которого заранее не известны.

Технический результат заключается в определении параметров сигнала с неизвестной структурой и последующей демодуляцией данного сигнала. Данный результат достигается благодаря применению двухуровневой обработки сигнала. При этом данные, полученные в ходе первичной обработки, настраивают систему для более детальной вторичной обработки. Структура параллельной обработки в нейронной сети позволяет сократить вычислительные затраты и скорректировать работу системы по результатам вторичной обработки. Предлагаемая система автоматически перестраивает структуру нейронной сети под любой сигнал, после чего время обработки резко сокращается и осуществляется демодуляция принятого сигнала.

1. Способ определения структуры и демодуляция сигнала с неизвестной структурой при помощи комплексного многоэтапного исследования характеристик сигнала на основе быстрого Фурье преобразования, изменения частоты дискретизации входного сигнала, регистрации и анализа спектрограмм, отличающийся тем, что обработку входного сигнала с неизвестной структурой производят в два этапа путем первичной вейвлет обработки, определяющей граничные значения параметров сигнала и вторичной обработки в нейронной сети, созданной на одном слое Кохонена, определяющей точные значения параметров сигнала, по результатам которой нейронную сеть модифицируют под исследуемый входной сигнал, после чего строят созвездие сигнала и осуществляют его демодуляцию при помощи стандартных или синтезированных приемников, автоматически подстраиваясь под входной сигнал с неизвестной структурой.

2. Способ определения структуры и демодуляция сигнала с неизвестной структурой по п.1, отличающийся тем, что алгоритм формирования весовых коэффициентов составных нейронов следующий: для каждого значения частоты, фазы и амплитуды вычисляют m гармоник с длительностью в один период и с разной начальной фазой, то есть данный скачок фазы входного сигнала как бы перемещают в разные точки периода, в результате формируют два вектора S_i (вектор с различными фазовыми скачками) и S_i0 (просто гармонический сигнал с различными частотами и амплитудами), после чего проводят обработку сигнала без начальной синхронизации, диапазон изменения весов каждого нейрона определяют шумовыми составляющими входного сигнала, таким образом, составные нейроны распознают входной сигнал в пределах "размытости" соответствующих весов.