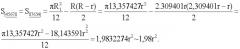Планиметрический способ контроля коррекции верхней зубной дуги

Планиметрический способ контроля коррекции верхней зубной дуги

Иллюстрации

Показать все

Реферат

Изобретение относится к области медицины, а именно к стоматологии, и может быть применено в ортодонтии.

Известен графический способ определения формы зубных дуг и расположения зубов в системе координат [Диагностика и функциональное лечение зубочелюстно-лицевых аномалий /Хорошилкина Ф.Я., Френкель Р., Демнер Л.М., Фальк Ф., Малыгин Ю.М., Френкель К. (Совместное издание СССР-ГДР). - М.: Медицина, 1987. - С.218-219; Ю.К.Петрова. Способ определения размеров зубных дуг в трансверсальном и сагиттальном направлениях. // Информационный листок ВНПО «Стоматология» МЗ СССР, 1990. Регистрационный №10-11/80] по размерам, полученным на моделях челюстей пациентов в различное время обследования (до лечения, после его окончания и при проверке отдаленных результатов) путем графического изображения формы зубной дуги, а также формы, которая должна быть в норме. Для этого на миллиметровой бумаге чертят систему координат, где ось ординат - срединная линия соответствующих челюстей (RR'), ось абсцисс для верхней зубной дуги - линия, проведенная через срединную точку резцового сосочка (PP'), перпендикулярно линии RR', для нижней зубной дуги - линия, проведенная через точку Пона на дистально расположенном моляре (MM'). На оси ординат откладывают размеры, отражающие сагиттальное расположение зубов, на оси абсцисс - размеры, отражающие их трансверсальное расположение. Из точек восстанавливают перпендикуляры к осям ординат и абсцисс, места пересечения которых соответствуют расположению измеряемой точки каждого верхнего и нижнего зуба. Полученные точки соединяют линиями. Изображение форм зубных дуг, имевшееся до лечения, в процессе лечения и после окончания лечения переносят на прозрачную перлоновую пленку и сопоставляют по линиям отсчета с целью выявления изменений расположения зубов.

Недостатки:

- условность обозначения расположения зубов в системе координат, что приводит к сложности и субъективности смыслового восприятия отклонений зубной дуги;

- определение расположения отдельных зубов в системе координат достаточно трудоемко;

- способ не предусматривает количественную оценку нарушений зубной дуги, т.е. недостоверен.

Известен способ изучения положения зубов и зубных дуг с помощью диагностического устройства и прозрачных трафаретов [И.В.Попова, Л.С.Персин, Г.В.Кузнецова. Диагностика аномалий зубов и зубных рядов с помощью прозрачных трафаретов. // Наука - практике: м-лы науч. Сессии ЦНИИС, посв. 35-летию института. - М., 1998. - С.240-243]. Для построения графического изображения зубной дуги авторы использовали способ Hawley-Herber-Herbst [И.И.Ужумецкене. Методы исследования в ортодонтии. - М.: Медицина, 1970] и в зависимости от суммы размеров резцов и клыков изготовили девять видов прозрачных трафаретов. Полученные трафареты накладывают на гипсовые модели челюстей, расположенные в диагностическом устройстве в соответствии с определенными на боковой телерентгенограмме головы направлением окклюзионной плоскости и положением координатной точки K и изучают расположение зубов, форму и размеры зубной дуги относительно координатной точки K.

Недостатки:

- применение способа невозможно без предварительного получения боковой телерентгенограммы головы;

- в описании построения диаграммы Hawley-Herber-Herbst не уточнены размеры боковых сегментов зубной дуги;

- способ не уточняет локализацию отклонений зубной дуги;

- в боковые сегменты было бы справедливо включить вторые моляры, сходные морфологически, функционально и эстетически с первыми молярами и активно участвующие в выполнении функции жевания.

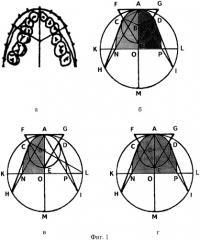
Способ определения отклонений постоянной зубной дуги, предложенный Hawley-Herber-Herbst [И.И.Ужумецкене. Методы исследования в ортодонтии. - М.: Медицина, 1970. - С.42-44], принят за ближайший аналог. Он заключается в том, что получают сумму ширины коронок центральных и боковых резцов и клыка верхней челюсти, затем путем геометрически-графического построения, в котором схематично изображают форму нормальной зубной дуги. Полученную диаграмму совмещают с зубной дугой для определения отклонений от нормы (Фиг.1,а).

Недостатки:

- способ Hawley-Herber-Herbst не дает конкретной оценки отклонений каждого или группы элементов от нормы;

- способ не позволяет достоверно выявить степень нарушений зубной дуги и/или зубов;

- способ субъективен и лишь ориентировочный при оценке, что не позволяет достаточно точно обеспечить алгоритм лечения.

Задачи:

- обеспечение возможности прогнозирования размеров всей зубной дуги и ее сегментов (длины и площади);

- обеспечение объективности оценки состояния зубной дуги и зубов пациента;

- обеспечение контроля коррекции зубной дуги, ее сегментов и зубов в динамике.

Техническим результатом предлагаемого способа является достоверное определение отклонения зубной дуги от нормы путем планиметрического моделирования сегментов и зубной дуги в целом, определения площадей отдельных сегментов зубной дуги, уточнения локализации наибольшей деформации зубной дуги, обеспечения достоверного контроля эффективности коррекции зубной дуги в динамике.

Заявленный способ контроля коррекции верхней зубной дуги включает построение диаграммы верхней зубной дуги пациента по Хаулею-Герберу-Гербсту. При этом за норму принимают следующие показатели: площадь каждого из сегментов АВС и ABD равна 0,52 r², площадь каждого из сегментов CBON и DBOP равна 1,98 r², прогнозируемую длину зубной дуги - 5,92 r, прогнозируемую длину половины зубной дуги 2,96 r, прогнозируемую длину СА 1,05 r и AD 1,05 r, прогнозируемую длину CN - 1,91 r и длину DP - 1,91 r, где r - радиус окружности с центром в точке В. Затем в динамике результаты лечения определяют по приближению истинных значений к должным.

Способ осуществляют следующим образом.

Получают сумму ширины коронок центральных и боковых резцов и клыка верхней челюсти и путем геометрически-графического построения по способу Hawley-Herber-Herbst схематично изображают форму нормальной зубной дуги (Фиг.1,б).

Зубную дугу условно разделяют на четыре сегмента: АВС, ABD, CBON, DBOP. В передние сегменты АВС и ABD включают центральные и боковые резцы и клыки (3211 и 1123), а в боковые CBON и DBOP - клыки, премоляры и моляры (876541 и 145678).

Определяют площади передних сегментов зубной дуги. Согласно методу Hawley-Herber-Herbst передние сегменты зубной дуги занимают сектор CADB (Фиг.1,б) окружности радиусом r, равным сумме ширины коронок центрального и бокового резцов и клыка, где AB=CB=DB=AC=AD=r. Отсюда ΔABC и ΔABD - равносторонние, углы которых равны 60°, a ∠CBD=120°. Следовательно, сектор CBD является ⅓ частью окружности с радиусом r.

Отсюда площадь сектора CBD равна

а площади секторов соответственно

Далее определяют площади боковых сегментов зубной дуги. Боковые сегменты CBON и DBOP зубной дуги (Фиг.1,в) в норме равны друг другу. При этом СВ=r, где r - радиус малой окружности с центром в точке В; ВО=R-r, где R - радиус большой окружности с центром в точке О; ON=R₁-R, где R₁ - радиус окружности с центром в точке L. Площадь фигуры CBON (S_CBON) можно определить как разницу между площадью сектора LCN (S_LCN) и треугольника ΔLBO (S_LBO).

Для определения S_LCN вычисляют величину угла ∠CLN: ∠LBO=∠ABC=60°; ∠BOL=90°, отсюда ∠CLN=30°. Следовательно, S_LCN=1/12πR₁ ².

Площадь треугольника ΔLBO равна

отсюда

Аналогично вычисляют площадь фигуры DBOP (S_DBOP). Таким образом, площади боковых сегментов зубных дуг в норме определяют по формуле

Далее выражают R через r.

Стороны треугольников ΔDAB и ΔСАВ равны r, следовательно, они равносторонние, a ∠DAB=∠CAB=60°; ∠GAD=∠FAC=30°, отсюда ∠AGD=∠AFC=60°. Следовательно, треугольник ∆FGE равносторонний, стороны которого FG=FE=EG=АО=R, следовательно, FA=AG=1/2R. В прямоугольном треугольнике ΔAEG квадрат гипотенузы EG равен сумме квадратов катетов AG и АЕ, где AG=1/2R, АЕ=2r:

R²=(1/2R)²+(2r)²=1/4R²+4r²,

R²=1/4R²+4r², или R²-1/4R²=4r², или 3/4R²=4r², или R²=16/3r²,

Далее выражают R₁ через r.

В треугольнике ΔLBO сторона LB=(R₁-r); сторона BO равна (R-r); сторона OL=R. Треугольник ΔLBO - прямоугольный, поэтому квадрат гипотенузы LB равен сумме квадратов катетов BO и OL, или

(R₁-r)²=(R-r)²+R², где или R= 2,309401r,

отсюда

или R₁=3,654781r.

В формулу

вставляют значения R₁ и R

Таким образом,

Определяют длину передних сегментов зубной дуги.

Длина СА в норме равна длине АД или

Определяют длину боковых сегментов зубной дуги.

Длина CN в норме равна длине ДР или

Это позволяет прогнозировать должную длину боковых сегментов, включающих зубы: 1-й и 2-й премоляры, 1-й, 2-й и 3-й моляры.

Таким образом, практически должная площадь всей зубной дуги должна быть принята равной 5,0 r², площадь половины зубной дуги - 2,5 r², площадь переднего сегмента зубной дуги - 0,52 r², площадь бокового сегмента зубной дуги - 1,98 r²; прогнозируемая длина зубной дуги - 5,92 r², прогнозируемая длина половины зубной дуги - 2,96 r, прогнозируемая длина переднего сегмента зубной дуги - 1,05 r, прогнозируемая длина бокового сегмента зубной дуги - 1,91 r.

Клинический пример

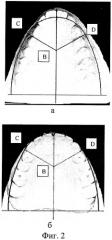
Диагностическая модель верхней челюсти пациента М., 12 лет, до лечения (Фиг.2,а) и после лечения (Фиг.2,б), в возрасте 14 лет. Выявленные путем измерений по методам Pont, Korkhaus аномалии: сужение верхней зубной дуги в области премоляров и моляров, удлинение его переднего отдела.

Выполнили следующие расчеты:

1) измерили и суммировали мезиодистальные размеры центрального, бокового разцов и клыка слева и справа:

среднее значение r=22,05;

2) определили прогнозируемую площадь передних ее сегментов:

3) определили прогнозируемую площадь боковых сегментов зубной дуги:

4) определили прогнозируемую площадь половины зубной дуги:

5) определили прогнозируемую площадь всей зубной дуги:

6) вычислили прогнозируемую длину боковых сегментов зубных дуг

по формуле 1,91 r:

1,91×22,05=42,12;

7) прогнозируемую ширину коронки третьего моляра определили по формуле

где 33,15 - среднее значение суммы ширины коронок премоляров и моляров, равное полусумме

(33,2+33,1):2=33,15.

Для контроля коррекции зубной дуги, ее половины и/или сегментов на сканированное изображение диагностической модели наложили графическое изображение индивидуальной нормальной зубной дуги и при помощи миллиметровой сетки определили площадь зубной дуги, площадь половины зубной дуги, площадь передних сегментов зубной дуги, площадь боковых сегментов зубной дуги.

Использование персонального компьютера значительно упрощает применение планиметрического способа контроля коррекции верхней зубной дуги, сводит к минимуму временные затраты, необходимые для расчетов.

Медико-социальная эффективность

Способ позволяет врачу объективно оценить отклонения зубной дуги от должной, уточнить локализацию наибольшей деформации зубной дуги, прогнозировать возможности ортодонтической коррекции зубной дуги, достоверно контролировать результаты коррекции зубной дуги, ее сегментов и зубов в динамике.

Планиметрический способ контроля коррекции верхней зубной дуги, включающий построение диаграммы верхней зубной дуги пациента по Хаулею - Герберу - Гербсту, отличающийся тем, что за норму принимают следующие показатели: площадь каждого из сегментов АВС и ABD равна 0,52 r², площадь каждого из сегментов CBON и DBOP равна 1,98 r², прогнозируемую длину зубной дуги - 5,92 r, прогнозируемую длину половины зубной дуги - 2,96 r, прогнозируемую длину СА - 1,05 r и AD - 1,05 r, прогнозируемую длину CN - 1,91 r, и длину DP - 1,91 r, где r - радиус окружности с центром в точке В, затем в динамике результаты лечения определяют по приближению истинных значений к должным.