Способ сжатия и восстановления речевых сообщений

Способ сжатия и восстановления речевых сообщений

Иллюстрации

Показать все

Реферат

Изобретение относится к области электросвязи, а именно к области, связанной с сокращением избыточности и криптографической защитой передаваемой информации. Предлагаемый способ может быть использован для передачи речевых сообщений по цифровым каналам связи в зашифрованном виде со скоростью до 4 кбит/с. Способ кодирования речевого сигнала может быть отнесен к классу способов кодирования формы речевого сигнала или способов непосредственного кодирования-восстановления, а защита информации - к классу способов на основе суммирования открытой информации с псевдослучайной последовательностью (ПСП).

Известны способы кодирования формы речевого сигнала, см., например, книгу: Дж.Кейтер Компьютеры - синтезаторы речи М.: Мир, 1985, с.87-103, включающие выполнение трех операций: временную дискретизацию аналоговых сигналов, их квантование и кодирование (представление квантованных дискретных отсчетов речевого сигнала двоичными цифрами). Рассматриваемый способ главным образом определяет механизм кодирования и декодирования квантованных дискретных отсчетов речевого сигнала.

Известны также способы кодирования дискретных квантованных отсчетов речевого сигнала на основе дельта-модуляции, адаптивной дельта-модуляции, импульсно-кодовой модуляции, дифференциальной импульсно-кодовой модуляции, метода блочного кодирования с ортогональным преобразованием, см., например, книгу: М.В.Назаров, Ю.Н.Петров Методы цифровой обработки и передачи цифровых сигналов. - М.: Радио и связь, 1985, с.142-161. Недостатком перечисленных выше способов - аналогов является относительно низкая информационная эффективность, под которой понимается достижение определенного качества восстановления речевой информации при заданной скорости передачи. В рассмотренных способах - аналогах приемлемое качество восстановления речевой информации достигается при скорости передачи более 16 кбит/с.

Известны также способы шифрования информации на основе суммирования открытой информации с ПСП, см. например, книгу Рябко Б.Я., Фионов А.Н. Криптографические методы защиты информации: Учебное пособие для вузов. - М.: Горячая линия - Телеком, 2005, стр.179-184. Недостатком данных способов является то, что необходимая стойкость шифрования достигается только в случае, если ПСП образована из независимых и равновероятных символов и используется только один раз. Это приводит к необходимости генерировать случайные последовательности очень большого периода и обеспечивать их синхронизацию как на передающей, так и на приемной сторонах.

Наиболее близким по своей технической сущности к заявленному способу сжатия и восстановления речевых сообщений является способ, описанный в патенте России №2152646 А, МПК⁷ G10L 3/02 от 2000 г.

Известный способ-прототип заключается в том, что предварительно на передающей и приемной сторонах идентично генерируют случайную квадратную матрицу квантованных отсчетов размером m×m элементов, каждый отсчет которой принадлежит диапазону квантованных дискретных отсчетов речевого сигнала, дискретизации непрерывного сигнала, квантовании дискретных отсчетов, формировании матрицы квантованных отсчетов речевого сигнала размером N×N элементов, преобразовании матрицы квантованных отсчетов речевого сигнала размером N×N элементов к цифровому виду путем формирования множества нулевых и единичных элементов в виде прямоугольных матриц размером N×m и m×N элементов, для чего на передаче предварительно генерируют случайные прямоугольные матрицы из единичных и нулевых элементов размером N×m и m×N, преобразуют их путем деления элементов каждой строки матрицы размером N×m элементов на сумму единиц соответствующей строки и деления элементов каждого столбца матрицы размером m×N элементов на сумму единиц соответствующего столбца, вычисляют матрицу размером N×N элементов путем перемножения полученных после преобразования прямоугольных матриц с ранее идентично сформированной на передаче и приеме квадратной матрицей квантованных отсчетов размером m×m элементов, вычисляют сумму квадратов разностей между элементами полученной в результате перемножения матрицы размером N×N и элементами матрицы квантованных отсчетов речевого сигнала размером N×N элементов, затем последовательно инвертируют каждый элемент предварительно сгенерированных случайным образом прямоугольных матриц размером m×N и N×m элементов, преобразуют их, а затем перемножают прямоугольные матрицы размером m×N и N×m элементов с ранее сформированной матрицей квантованных отсчетов размером m×m элементов, вычисляют сумму квадратов разностей между элементами полученной в результате перемножения матрицы размером N×N и элементами матрицы квантованных отсчетов речевого сигнала, вычитают эту сумму от аналогичной суммы, полученной на предыдущем шаге и, в случае положительной разности, сохраняют инвертированное значение элемента, а в противном случае выполняют его повторную инверсию, передаче сформированных прямоугольных матриц размером N×m и m×N элементов в канал связи, приеме из канала связи, преобразовании их путем деления элементов каждой строки матрицы размером N×m элементов на сумму единиц соответствующей строки и деления элементов каждого столбца матрицы размером m×N элементов на сумму единиц соответствующего столбца, восстановлении матрицы квантованных отсчетов речевого сигнала размером N×N элементов путем перемножения полученных после преобразования прямоугольных матриц размером N×m и m×N элементов и ранее сформированной квадратной матрицы квантованных дискретных отсчетов размером m×m элементов и обратном преобразовании квантованных дискретных отсчетов в непрерывный речевой сигнал.

Недостатком этого способа-прототипа является отсутствие криптографической защиты передаваемой по цифровому каналу связи информации в виде множества нулевых и единичных элементов прямоугольных матриц размером N×m и m×N элементов. Следствием этого является доступ незаконных получателей к содержанию передаваемой информации.

Целью изобретения является разработка способа сжатия и восстановления речевых сообщений, обеспечивающего требуемую стойкость криптографической защиты передаваемой информации и не требующего в процессе шифрования обмена случайными последовательностями, которые необходимы для работы традиционных систем шифрования.

Поставленная цель достигается тем, что в предлагаемом способе сжатия и восстановления речевых сообщений предварительно на передающей и приемной сторонах идентично генерируют случайную квадратную матрицу квантованных отсчетов размером m×m элементов, каждый отсчет которой принадлежит диапазону квантованных дискретных отсчетов речевого сигнала, генерируют две случайные ключевые матрицы размером N×m и m×N элементов. А на передающей стороне генерируют случайный вектор номеров инверсий размером N элементов (I_1×N). Дискретизируют непрерывный сигнал и квантовантуют дискретные отсчеты. Далее формируют матрицы квантованных отсчетов речевого сигнала размером N×N элементов, преобразовании матрицы квантованных отсчетов речевого сигнала размером N×N элементов к цифровому виду путем формирования множества нулевых и единичных элементов в виде прямоугольных матриц размером N×m и m×N элементов. Для чего на передаче предварительно генерируют случайные прямоугольные матрицы из единичных и нулевых элементов размером N×m и m×N, преобразуют их путем деления элементов каждой строки матрицы размером N×m элементов на сумму единиц соответствующей строки и деления элементов каждого столбца матрицы размером m×N элементов на сумму единиц соответствующего столбца. Затем вычисляют матрицу размером N×N элементов путем перемножения полученных после преобразования прямоугольных матриц с ранее идентично сформированной на передаче и приеме квадратной матрицей квантованных отсчетов размером m×m элементов. Вычисляют сумму квадратов разностей между элементами полученной в результате перемножения матрицы размером N×N и элементами матрицы квантованных отсчетов речевого сигнала размером N×N элементов. Затем инвертируют каждый элемент случайных прямоугольных матриц размером N×m и m×N элементов в последовательности, определенной соответствующими элементами случайного вектора номеров инверсий размером m×N элементов. Преобразуют их, а затем перемножают прямоугольные матрицы размером m×N и N×m элементов с ранее сформированной матрицей квантованных отсчетов размером m×m элементов и вычисляют сумму квадратов разностей между элементами полученной в результате перемножения матрицы размером N×N и элементами матрицы квантованных отсчетов речевого сигнала. Вычитают эту сумму от аналогичной суммы, полученной на предыдущем шаге и, в случае положительной разности, сохраняют инвертированное значение элемента, а в противном случае выполняют его повторную инверсию. Суммируют множества нулевых и единичных элементов в виде прямоугольных матриц размером N×m и m×N элементов по модулю два со случайными ключевыми матрицами размером N×m и m×N элементов. Передают матрицы размером N×m и m×N элементов в канал связи. Принимают матрицы размером N×m и m×N из канала связи, суммируют их по модулю два со случайными ключевыми матрицами размером N×m и m×N элементов и преобразовании их путем деления элементов каждой строки матрицы размером N×m элементов на сумму единиц соответствующей строки и деления элементов каждого столбца матрицы размером m×N элементов на сумму единиц соответствующего столбца, восстановлении матрицы квантованных отсчетов речевого сигнала размером N×N элементов путем перемножения полученных после преобразования прямоугольных матриц размером N×m и m×N элементов и ранее сформированной квадратной матрицы квантованных дискретных отсчетов размером m×m элементов и обратном преобразовании квантованных дискретных отсчетов в непрерывный речевой сигнал. Для формирования вектора номеров инверсий предварительно генерируют N×m неповторяющихся целых чисел (а) в диапазоне от 1 до N и записывают их по правилу I_m×N(i)=а.

Заявленный способ поясняется чертежами:

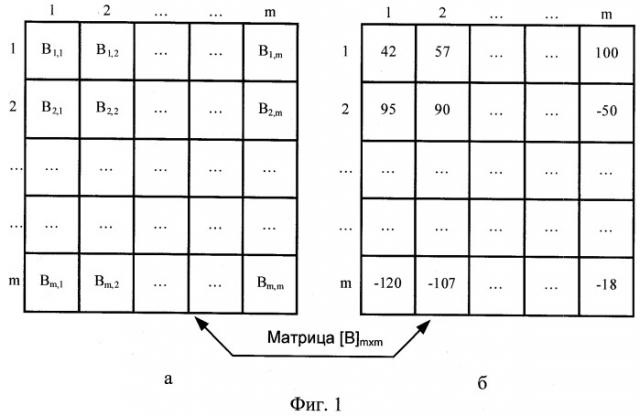
Фиг.1а - формирование случайной квадратной матрицы квантованных дискретных отсчетов размером m×m элементов;

Фиг.1б - вариант случайной квадратной матрицы квантованных дискретных отсчетов размером m×m элементов;

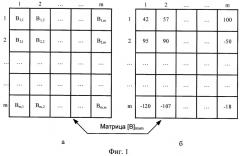
Фиг.2а - формирование случайной ключевой матрицы размером N×m элементов;

Фиг.2б - вариант случайной ключевой матрицы размером N×m элементов;

Фиг.2в - формирование случайной ключевой матрицы размером m×N элементов;

Фиг.2г - вариант случайной ключевой матрицы размером m×N элементов;

Фиг.3 - пример формирования вектора номеров инверсий размером 1×N элементов;

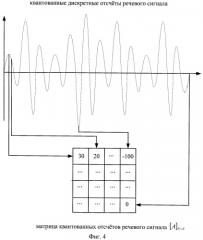
Фиг.4 - пример формирования матрицы квантованных отсчетов речевого сигнала размером N×N элементов;

Фиг.5 - преобразование множества нулевых и единичных элементов прямоугольных матриц размером N×m и m×N элементов на основе случайных ключевых матриц размером N×m и m×N элементов;

Фиг.6а - пример формирования прямоугольных матриц размером N×m и m×N элементов на основе первого вектора случайных инверсий.

Фиг.6б - пример формирования прямоугольных матриц размером N×m и m×N элементов на основе второго вектора случайных инверсий.

Фиг.7 - последовательная оптимизация элементов матриц и ;

Фиг.8а - преобразование случайной прямоугольной матрицы размером N×m элементов;

Фиг.8б - преобразование случайной прямоугольной матрицы размером m×N элементов;

Фиг.9 - вариант инверсий элемента случайной прямоугольной матрицы размером N×m элементов на основе вектора номеров инверсий размером 1×N элементов.

Возможность реализации заявленного способа сжатия и восстановления речевых сообщений объясняется следующим. Существует традиционный подход, когда с целью криптографической защиты информации на передающей и приемной сторонах формируют идентичные ПСП с максимальным периодом. Примеры такого подхода известны как различные модификации потоковых шифров, например шифр Вернама. Данные шифры имеют существенный недостаток. Он состоит в том, что для обеспечения требуемой стойкости необходимо при шифровании каждого нового сообщения использовать новую случайно формируемую последовательность, длина которой равна длине открытого сообщения, либо использовать последовательности, порожденные при помощи генераторов псевдослучайных чисел. Однако в этом случае возникает необходимость передачи по цифровому каналу связи на приемную сторону начального состояния генератора передачи, в виде случайной последовательности.

В предлагаемом способе начальное состояние генератора по цифровому каналу связи не передается. В качестве ПСП в предлагаемом способе используются две случайные ключевые матрицы размером N×m и m×N элементов, которые предварительно идентично генерируют на передающей и приемной сторонах и не изменяют в процессе функционировании кодера и декодера. Для шифрования информации данные матрицы суммируют по модулю два с преобразованными прямоугольными матрицами размером N×m и m×N элементов. Однако в соответствии с традиционными подходами для обеспечения стойкости шифрования при кодировании новых сообщений используемые две случайные ключевые матрицы должны изменяться. Это изменение может быть достигнуто путем их доставки на передающую и приемную стороны по заведомо стойким каналам связи, либо путем передачи по каналу связи начального состояния генератора, который сформирует на приемной стороне ключевую матрицу, идентичную ключевой матрице, сформированной на передающей стороне. В предлагаемом способе "эффект изменения" случайных ключевых матриц достигается следующим.

При кодировании каждого нового сообщения вносится элемент случайности при поиске преобразованных случайных прямоугольных матриц размером N×m и m×N элементов. Этот элемент случайности реализуется за счет случайного начального заполнения этих матриц и случайного формирования вектора номеров инверсий размером N×m и m×N элементов в процессе поиска. В результате этого даже при кодировании одного и того же речевого фрагмента найденные преобразованные случайные прямоугольные матрицы размером N×m и m×N элементов будут различны. Поэтому в предлагаемом способе эффект изменения ключевых матриц заменяется случайными изменениями прямоугольных матриц размером N×m и m×N элементов, определенных на этапе поиска при кодировании каждого нового сообщения. Таким образом, суммирование по модулю два случайно измененных, при каждом новом кодировании, прямоугольных матриц размером N×m и m×N элементов с неизменяемыми ключевыми матрицами размером N×m и m×N элементов заменяет подход основанный на традиционном способе шифрования, который заключается в суммированием по модулю два найденных прямоугольных матриц размером N×m и m×N элементов со случайно изменяемыми ключевыми матрицами размером N×m и m×N элементов.

Предлагаемый способ реализуют следующим образом.

Формирование на передающей и приемной сторонах случайной квадратной матрицы квантованных дискретных отсчетов , каждый отсчет которой принадлежит диапазону квантованных дискретных отсчетов речевого сигнала, как показано на фиг.1. Формирование может быть выполнено на основе датчика случайных чисел, например на основе шумового диода. Для выполнения требования идентичности матрицы приемника аналогичной матрице передатчика перед началом каждого сеанса связи элементы матрицы могут быть сгенерированы на передаче и переданы по цифровому каналу связи на приемную сторону, например, в составе синхропосылки. Затем на передающей и приемной сторонах идентично генерируют случайные ключевые матрицы размером N×m и m×N элементов и (фиг.2), генерация их может быть выполнена также на основе датчика случайных чисел, например, на основе шумового диода. Генерируют случайный вектор номеров инверсий размером N элементов (I_1×N). Для формирования вектора номеров инверсий предварительно генерируют N неповторяющихся целых чисел (а) в диапазоне от 1 до N и записывают их по правилу I_m×N(i)=а. Формирование вектора номеров инверсий показано на фиг.3.

Дискретизацию непрерывного речевого сигнала выполняют в соответствии с теоремой Котельникова. В предлагаемом способе выбрана общепринятая частота дискретизации непрерывного речевого сигнала 8 кГц. Затем осуществляют квантование дискретных отсчетов. Квантование осуществляется на основе способов, описанных, например, в кн.: М.В.Назаров, Ю.Н.Петров. Методы цифровой обработки и передачи цифровых сигналов. - М.: Радио и связь, 1985, с.142-161. Далее, на основе множества квантованных дискретных отсчетов речевого сигнала осуществляют формирование матрицы квантованных отсчетов речевого сигнала . Формирование матрицы квантованных отсчетов речевого сигнала показано на фиг.4. При этом матрица квантованных отсчетов формируется из N² квантованных дискретных отсчетов речевого сигнала каждому элементу которой A_ji, где j=1, 2, …, N; i=1, 2, …, N, присваивают квантованное значение отсчета речевого сигнала, k-й номер которого определяют в соответствии с выражением: k=j+N·(i-1).

Для преобразования матрицы квантованных отсчетов речевого сигнала к цифровому виду на передаче формируют множество нулевых и единичных элементов в виде матриц и (процедура, реализующая поиск на передаче оптимальных матриц и подробно описана в приложении 1), затем полученное множество поэлементно суммируют по модулю два со случайными ключевыми матрицами и , как показано на фиг.5, и результат передают по каналу связи.

После приема из цифрового канала связи матриц и суммируют их по модулю два со случайными ключевыми матрицами и , и результат преобразуют в матрицы и соответственно. Преобразование выполняют путем деления элементов каждой строки матрицы на сумму единиц соответствующей строки и деления элементов каждого столбца матрицы на сумму единиц соответствующего столбца. После этого восстанавливают матрицу квантованных отсчетов речевого сигнала в соответствии с выражением: и выполняют обратное преобразование из матрицы восстановленных квантованных отсчетов речевого сигнала в непрерывный речевой сигнал.

Для оценки эффективности предлагаемого способа сжатия и восстановления речевых сообщений было проведено имитационное моделирование на ПЭВМ. При кодировании речевых сообщений использовалось 8-разрядное АЦП. При этом размер кодируемого блока составлял 24×24 элемента, что обеспечивало задержку передачи речи 0,72 мс. Размер случайной квадратной матрицы квантованных дискретных отсчетов составлял 12×12 элементов. В предлагаемом способе стойкость шифрования обеспечивается тем, что при кодировании каждого нового сообщения вносится элемент случайности при поиске преобразованных случайных прямоугольных матриц размером N×m и m×N элементов. Этот элемент случайности реализуется за счет случайного начального заполнения этих матриц и случайного формирования вектора номеров инверсий размером N×m и m×N элементов в процессе поиска. В результате этого даже при кодировании одного и того же речевого фрагмента найденные преобразованные случайные прямоугольные матрицы размером N×m и m×N элементов будут различны. Экспериментальные исследования показали, что при изменении вектора номеров инверсий происходит изменение множества нулевых и единичных элементов в виде матриц и почти в половине элементов (фиг.6), что в свою очередь соответствует требованию по стойкости криптографических систем.

При этом достигаемый коэффициент сжатия (коэффициент уменьшения требуемой скорости передачи цифрового потока) может быть определен по формуле

,

где L - число уровней квантования дискретных отсчетов речевого сигнала.

При выборе N=24, m=12 (L=256) обеспечивался коэффициент сжатия 8 раз (скорость передачи на выходе кодера - 8 [кбит/с]). При выборе размера случайной квадратной матрицы квантованных дискретных отсчетов речевого сигнала 6*6 элементов коэффициент сжатия речевых сообщений составил 16 раз (скорость передачи на выходе кодера - 4 [кбит/с]). Качество восстановленной речи на приеме оценивалось по соотношению сигнал/шум и составило около 14 [db]. При этом восстановленная речь сохраняет свою естественность, натуральность и обладает хорошей разборчивостью.

1. Способ сжатия и восстановления речевых сообщений, заключающийся в том, что предварительно на передающей и приемной сторонах идентично генерируют случайную квадратную матрицу квантованных отсчетов размером m×m элементов, каждый отсчет которой принадлежит диапазону квантованных дискретных отсчетов речевого сигнала, дискретизации непрерывного сигнала, квантовании дискретных отсчетов, формировании матрицы квантованных отсчетов речевого сигнала размером N×N элементов, преобразовании матрицы квантованных отсчетов речевого сигнала размером N×N элементов к цифровому виду путем формирования множества нулевых и единичных элементов в виде прямоугольных матриц размером N×m и m×N элементов, для чего на передаче предварительно генерируют случайные прямоугольные матрицы из единичных и нулевых элементов размером N×m и m×N, преобразуют их путем деления элементов каждой строки матрицы размером N×m элементов на сумму единиц соответствующей строки и деления элементов каждого столбца матрицы размером m×N элементов на сумму единиц соответствующего столбца, вычисляют матрицу размером N×N элементов путем перемножения полученных после преобразования прямоугольных матриц с ранее идентично сформированной на передаче и приеме квадратной матрицей квантованных отсчетов размером m×m элементов, вычисляют сумму квадратов разностей между элементами полученной в результате перемножения матрицы размером N×N и элементами матрицы квантованных отсчетов речевого сигнала размером N×N элементов, затем инвертируют каждый элемент предварительно сгенерированных случайным образом прямоугольных матриц размером m×N и N×m элементов, преобразуют их, а затем перемножают прямоугольные матрицы размером m×N и N×m элементов с ранее сформированной матрицей квантованных отсчетов размером m×m элементов, вычисляют сумму квадратов разностей между элементами полученной в результате перемножения матрицы размером N×N и элементами матрицы квантованных отсчетов речевого сигнала, вычитают эту сумму из аналогичной суммы, полученной на предыдущем шаге, и в случае положительной разности сохраняют инвертированное значение элемента, а в противном случае выполняют его повторную инверсию, передаче сформированных прямоугольных матриц размером N×m и m×N элементов в канал связи, приеме из канала связи, преобразовании их путем деления элементов каждой строки матрицы размером N×m элементов на сумму единиц соответствующей строки и деления элементов каждого столбца матрицы размером m×N элементов на сумму единиц соответствующего столбца, восстановлении матрицы квантованных отсчетов речевого сигнала размером N×N элементов путем перемножения полученных после преобразования прямоугольных матриц размером N×m и m×N элементов и ранее сформированной квадратной матрицы квантованных дискретных отсчетов размером m×m элементов и обратном преобразовании квантованных дискретных отсчетов в непрерывный речевой сигнал, отличающийся тем, что предварительно идентично на приемной и передающей сторонах генерируют две случайные ключевые матрицы размером N×m и m×N элементов, на передающей стороне генерируют случайный вектор номеров инверсий размером m×N элементов (I_m×N), после вычисления суммы квадратов разностей между элементами полученной в результате перемножения матрицы размером N×N элементов и элементами матрицы квантованных отсчетов речевого сигнала размером N×N элементов инвертируют каждый элемент случайных прямоугольных матриц размером N×m и m×N элементов в последовательности, соответствующей элементам случайного вектора номеров инверсий размером m×N элементов, после формирования множества нулевых и единичных элементов в виде прямоугольных матриц размером N×m и m×N элементов суммируют их по модулю два со случайными ключевыми матрицами размером N×m и m×N элементов, после приема из канала связи матриц размером N×m, m×N элементов суммируют их со случайными ключевыми матрицами размером N×m и m×N элементов.

2. Способ по п.1, отличающийся тем, что для формирования вектора номеров инверсий предварительно генерируют N×m неповторяющихся целых чисел (а) в диапазоне от 1 до N×m и записывают их по правилу I_m×N(i)=a.