Способ частотно-временного корреляционного анализа цифровых сигналов

Способ частотно-временного корреляционного анализа цифровых сигналов

Иллюстрации

Показать все

Реферат

Изобретение относится к области цифровой обработки сигналов и может быть использовано для анализа сигналов различного происхождения при решении задач неразрушающего контроля и диагностики оборудования на основе корреляционного анализа.

Известен способ определения корреляционной функции двух цифровых сигналов f₁(t_i) и f₂(t_i) с помощью быстрого преобразования Фурье, выбранный в качестве прототипа [Эммануил С.Айфичер, Барри У.Джервис. Цифровая обработка сигналов: практический подход. 2-е издание. - М.: Вильямс, 2008]. Сущность способа заключается в прямом преобразования Фурье двух сигналов в форме быстрого преобразования Фурье (БПФ) размерностью 2ⁿ, определении комплексно-сопряженного значения результатов прямого преобразования Фурье второго сигнала, попарного умножения полученных комплексных сигналов прямого преобразования Фурье первого сигнала с комплексно-сопряженными значениями прямого преобразования Фурье второго сигнала. Полученные значения подвергают обратному преобразованию Фурье с целью получения информации в области времени.

Недостатком такого решения является то, что полученная корреляционная функция не позволяет оценить взаимосвязь сигналов на разных частотах.

Задачей изобретения является расширение возможностей анализа корреляции сигналов в частотной области.

Это достигается тем, что в способе частотно-временного корреляционного анализа цифровых сигналов, так же как в прототипе, включающем прямое преобразование Фурье в форме быстрого преобразования Фурье входных сигналов размерностью 2ⁿ, определении комплексно-сопряженного значения результатов прямого преобразования одного из сигналов, попарного умножения полученных комплексных сигналов прямого преобразования Фурье с комплексно-сопряженными значениями прямого преобразования Фурье второго сигнала, согласно изобретению из полученного произведения P_j выбирают значения и формируют m сигналов M^k,

где j=0, 1, …, 2^n-1+1;

m=2, 3, …, 2^n-1+1;

k=0, 1, …, m-1,

согласно выражению

Полученные сигналы M^k подвергают обратному преобразованию Фурье Z^k=F^-l[M^k]. По результатам обратного преобразования Фурье определяют частотно-временную корреляционную функцию

где t_i∈[t_min, t_max];

f_k∈[f_min, f_max];

f_d - частота дискретизации сигнала.

По полученным результатам строят график частотно-временной корреляционной функции r_l2(f, t), по которому судят о корреляции гармонических составляющих сигналов на различных частотах.

Заявленный способ частотно-временного корреляционного анализа цифровых сигналов имеет существенное преимущество, так как позволяет выявить подобие сигналов в частотной области за счет выбора из произведения P_j и формирования m сигналов M^k согласно приведенному выражению (1), что позволяет провести корреляционный анализ сигналов по m частотам и обеспечевает высокое быстродействие и универсальность реализации способа.

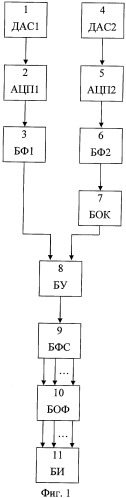
На фиг.1 приведена аппаратная схема устройства, реализующего рассматриваемый способ частотно-временного корреляционного анализа цифровых сигналов.

В табл.1 приведены исходные данные и результаты анализа тестовых примеров при m=281.

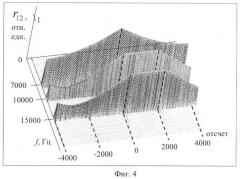
На фиг.2-4 приведены графики частотно-временной корреляционной функции результатов анализа тестовых примеров.

Заявленный способ частотно-временного корреляционного анализа цифровых сигналов может быть осуществлен с помощью схемы (фиг.1), содержащей первый датчик для получения анализируемого сигнала 1 (ДАС1), подключенный к первому блоку аналого-цифрового преобразования 2 (АЦП1), выход которого соединен с входом первого блока прямого преобразования Фурье 3 (БФ1), второй датчик анализируемого сигнала 4 (ДАС2), к которому последовательно подключены второй блок аналого-цифрового преобразования 5 (АЦП2), второй блок прямого преобразования Фурье 6 (БФ2) и блок определения комплексно-сопряженного значения 7 (БОК). Выходы первого блока прямого преобразования Фурье 3 (БФ1) и блока определения комплексно-сопряженного значения 7 (БОК) соединены с входом блока умножения 8 (БУ), к которому последовательно подключены блок формирования сигналов 9 (БФС), блок обратного преобразования Фурье 10 (БОФ) и блок интерпретации 11 (БИ).

В качестве датчиков анализируемого сигнала 1 (ДАС1) и 4 (ДАС2) могут быть использованы датчики тока, например промышленные приборы КЭИ-0.1 или датчики напряжения - трансформаторы напряжения (220/5 В). Блоки аналого-цифрового преобразования 2 (АЦП1) и 5 (АЦП2) могут быть реализованы на основе аналого-цифровых преобразователей ADS7827. Блоки прямого преобразования Фурье 3 (БФ1) и 6 (БФ2), блок определения комплексно-сопряженного значения 7 (БОК), блок умножения 8 (БУ), блок формирования сигналов 9 (БФС), блок обратного преобразования Фурье 10 (БОФ), блок интерпретации 11 (БИ) могут быть выполнены на микроконтроллере серии AVR32 производителя Atmel АТ32АР7000.

С выхода датчиков 1 (ДАС1) и 4 (ДАС2) анализируемые сигналы, например

y₁(t)=y₂(t)=u(t)=1·sin(2·π·700·t)+1·sin(2·π·10000·t)+

+1·sin(2·π·15000·t),

где u(t) - многочастотный сигнал напряжения (табл.1, пример №1), поступает на входы аналого-цифровых преобразователей 2 (АЦП1) и 5 (АЦП2), с выхода которых дискретизированные сигналы

y₁(t_i)=y₂(t_i)=u(t_i)=1·sin(2·π·700·t_i)+1·sin(2·π·10000·t_i)+

+1·sin(2·π·15000·t_i),

где t_i=Δt·i, где i=1, 2, …, n;

N=2ⁿ=2¹³=8192 - размер выборки для быстрого преобразования Фурье;

- шаг дискретизации сигнала u(t_i),

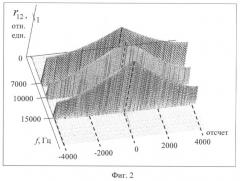
поступают на входы блоков прямого преобразования Фурье (в форме БПФ) 3 (БФ1) и 6 (БФ2), где выполняют прямое преобразование Фурье входных сигналов. С выхода блока прямого преобразования Фурье 6 (БФ2) результаты прямого преобразования Фурье в виде комплексного сигнала размерностью 2ⁿ⁺¹+1=4097 поступают на вход блока определения комплексно-сопряженного значения 7 (БОК), где определяют комплексно-сопряженные значения для каждого элемента сигнала. Результаты прямого преобразования Фурье БПФ 3 (БФ1) и блока определения комплексно-сопряженного значения 7 (БОК) поступают на вход блока умножения 8 (БУ), где выполняют попарное умножение двух комплексных сигналов. С выхода блока умножения 8 (БУ) результаты умножения в виде комплексного сигнала размерностью 2^n-1+1=4097 поступают на вход блока формирования сигналов 9 (БФС), где формируют m=281 комплексных сигналов размерностью 2^n-1+1=4097 согласно выражению (1). С выхода блока формирования сигналов 9 (БФС) полученные комплексные сигналы поступают на вход блока вычисления обратного преобразования Фурье 10 (БОФ), где выполняют обратное преобразование Фурье над каждым комплексным сигналом. С выхода блока вычисления обратного преобразования Фурье 10 (БОФ) результаты обратного преобразования Фурье в виде действительных m=281 сигналов размерностью N=2ⁿ=2¹³=8192 поступают на вход блока интерпретации 11 (БИ), где согласно выражению (2) определяют частотно-временную корреляционную функцию. Для m=281 и k=89 получили f_k=f₈₉=7008.75 Гц, r₁₂=0.9997, при k=127 получаем f_k=f₁₂₇=10001.25 Гц, r₁₂=0.9998, при k=191 получили f_k=f₁₉₁=15041.25 Гц, r₁₂=0.9996. Полученные частотно-временные корреляционные функции (фиг.2) ярко выражены на трех частотах, близких к частотам, заданным в тестовом примере, и принимают максимальные значения при нулевой задержке, что свидетельствует о совпадении двух анализируемых сигналов. Результат вычисления тестового примера в виде графика частотно-временной корреляционной функции представлен на фиг.2.

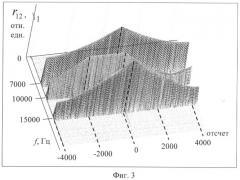
В табл.1 приведены тестовые примеры и результаты их расчета при m=281. На фиг.3 приведены частотно-временные корреляционные функции результата анализа тестового примера 2, по которым видно, что вторая гармоническая составляющая во втором сигнале запаздывает относительно второй гармонической составляющей первого сигнала на 1997 отсчетов. На фиг.4 приведены частотно-временные корреляционные функции результата анализа тестового примера 3, по которым видно, что вторая и третья гармонические составляющие первого сигнала запаздывают относительно второй и третьей гармонических составляющих второго сигнала на 1998 и 1997 отсчетов соответственно.

Таблица 1
СПОСОБ ЧАСТОТНО-ВРЕМЕННОГО КОРРЕЛЯЦИОННОГО АНАЛИЗА ЦИФРОВЫХ СИГНАЛОВ
№	Частота дискретизации, кГц	Размер выборки, отсчет	Сигнал	Параметры гармонических составляющих	Расчетная частота, Гц	Задержка, отсчет	Расчетное значение задержки, отсчет	Фиг.
Амплитуда, отн. едн.	Частота, кГц
1	44.1	8192	1	1	7	7008.75	0	0	2
				1	10	10001.25	0	0
				1	15	15041.25	0	0
			2	1	7	7008.75	0	0
				1	10	10001.25	0	0
				1	15	15041.25	0	0
2	44.1	8192	1	1	7	7008.75	0	0	3
				1	10	10001.25	0	0
				1	15	15041.25	0	0
			2	1	7	7008.75	0	0
				1	10	10001.25	2000	1997
				1	15	15041.25	0	0
3	44.1	8192	1	1	7	7008.75	0	0	4
				1	10	10001.25	2000	1998
				1	15	15041.25	2000	1997
			2	1	7	7008.75	0	0
				1	10	10001.25	0	0
				1	15	15041.25	0	0

Способ частотно-временного корреляционного анализа цифровых сигналов, включающий прямое преобразование Фурье в форме быстрого преобразования Фурье входных сигналов размерностью 2ⁿ, определение комплексно-сопряженного значения результатов прямого преобразования одного из сигналов, попарного умножения полученных комплексных сигналов прямого преобразования Фурье с комплексно-сопряженными значениями прямого преобразования Фурье второго сигнала, отличающийся тем, что из полученного произведения P_j выбирают значения и формируют m сигналов M^k,j=0, 1, …, 2^n-1+1;m=2, 3, …, 2^n-1+1;k=0, 1, …, m-1,согласно выражению полученные сигналы M^k подвергают обратному преобразованию Фурье Z^k=F^-1[M^K], определяют частотно-временную корреляционную функцию ,где t_i∈[t_min, t_max];f_k∈[f_min, f_max]; ; ; ; _; ; ;f_d - частота дискретизации сигнала,далее по полученным результатам строят график частотно-временной корреляционной функции r₁₂(f, t), по которому судят о корреляции гармонических составляющих сигналов на различных частотах.