Способ определения жесткости горизонтального шва в двухслойных конструкциях балочного типа

Способ определения жесткости горизонтального шва в двухслойных конструкциях балочного типа

Иллюстрации

Показать все

Реферат

Изобретение относится к области строительства и предназначено для определения жесткости горизонтальных швов в двухслойных конструкциях балочного типа.

Известен способ определения жесткости горизонтального шва ξ в двухслойных стержнях (или балках) составного сечения, который следует из выражения [1, с.13]

где Т_с - сдвигающее усилие, приходящееся на одну связь; n - число связей на единицу длины шва; Г - деформация взаимного сдвига смежных волокон двух соседних слоев. При реализации этого способа фрагмент испытуемого стержня устанавливают на специальном стенде, закрепляют нижний слой неподвижно, а к верхнему слою прикладывают сдвигающее усилие Т, замеряют величину абсолютного сдвига Г двух смежных волокон соседних слоев и определяют коэффициент жесткости горизонтального шва по формуле (1).

Этот способ имеет недостаток, который заключается в том, что его невозможно применить к стержню (или балке), стоящему непосредственно в сооружении.

Задача, на решение которой направлено изобретение, состоит в расширении технологических возможностей способа для его применения к длинномерным конструкциям, в том числе стоящим в сооружении, а также на снижение трудоемкости реализации способа.

Это достигается тем, что в способе определения коэффициента жесткости горизонтального шва двухслойной конструкции балочного типа, заключающемся в установке и закреплении конструкции на стенде, нагружении ее, измерении физических параметров, характеризующих деформированное состояние конструкции, и аналитическом вычислении коэффициента жесткости горизонтального шва, в шарнирно опертой по концам конструкции с помощью механического удара или внезапного снятия нагрузки возбуждают собственные поперечные колебания на основной частоте, или вынужденные колебания на первой резонансной частоте и измеряют эти частоты колебаний.

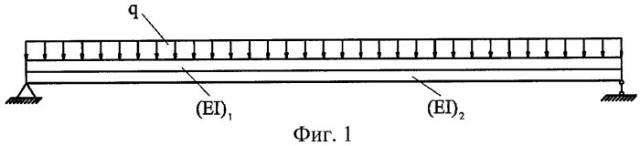
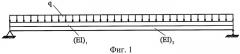
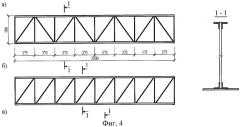
Осуществление заявляемого способа поясняется чертежами. На фиг.1 приведена расчетная схема двухслойной балки с шарнирными опорами, нагруженная равномерно распределенной нагрузкой; на фиг.2 представлены два типа регулярных решеток стальных ферм с параллельными поясами, которые используются в численном эксперименте; на фиг.4 представлены две схемы моделей ферм, использованных в натурном эксперименте; на фиг.5 приведена принципиальная схема динамических испытаний моделей ферм, включающая в себя опоры 1, испытываемую модель фермы 2, вибродатчик перемещений 3, виброанализатор «Вибран-2» 4, персональный компьютер 5.

Физическую сущность предлагаемого способа можно пояснить, используя теорию составных стержней, разработанную А.Р.Ржаницыным [1].

Расчет двухслойных балок составного сечения на изгиб сводится к решению дифференциального уравнения упругой оси балки [1, с.122]:

в котором

q - интенсивность равномерно распределенной нагрузки; E_i - модуль упругости материала слоев; A_i, I_i - соответственно площадь поперечного сечения и момент инерции каждого слоя балки; с - расстояние между центрами тяжести слоев составной балки; М₀ - изгибающий момент в рассматриваемом сечении балки. Далее индексы 1 и 2 относятся к физическим и геометрическим характеристикам первого и второго слоев балки.

Рассмотрим двухслойную шарнирно опертую балку, нагруженную равномерно распределенной нагрузкой q, изображенную на фиг.1. Ввиду геометрической и физической симметрии заданной системы начало координат выберем в середине пролета (l - половина пролета балки). В этом случае дифференциальное уравнение (1) примет следующий вид [1, с.125]:

Решением этого уравнения с учетом симметрии будет интеграл

где C₁ и C₂ - постоянные интегрирования, которые находят, используя граничные условия на конце балки у(l)=0 и у′′(l)=0:

,

где

С учетом этих постоянных выражение (7) преобразуется к виду

В середине пролета (при х=0) будем иметь [1, с.126]).

С помощью зависимости (9), используя математический аппарат сопротивления материалов, можно найти все необходимые характеристики напряженно-деформированного состоянии составной балки в любом ее сечении, если известно значение параметра ξ, входящего в выражение (3).

В работе [2, стр.137-140] была установлена фундаментальная закономерность в строительной механике

где m - погонная масса балки, которая связывает в аналитической форме величину максимального прогиба упругой однопролетной балки y₀ от действия равномерно распределенной нагрузки q с ее основной (круговой) частотой колебаний ω в ненагруженном состоянии. Вместо основной частоты колебаний можно использовать первую резонансную частоту колебаний конструкции в ненагруженном состоянии, поскольку для упругих конструкций эти частоты приблизительно равны [2, стр.22-24].

Ценность закономерности (11) заключается в том, что произведение y₀ω² не зависит от вида граничных условий, физических свойств материала, геометрических характеристик сечения и длины балки. Единственным условием ее применения является работа балки в упругом состоянии.

Используя выражения (10) и (11), можно записать

Откуда

или

где f=ω/(2π) - техническая частота колебаний (Гц). Полученное трансцендентное уравнение связывает неизвестный параметр λ, в который входит коэффициент жесткости шва ξ, с основной (или первой резонансной) частотой колебаний составной балки f. Эту частоту в контролируемой конструкции можно определить экспериментально, возбуждая в ней соответствующие колебания. Используя способ итераций, из выражения (14) можно вычислить значение параметра λ, а с помощью зависимости (2) - значение коэффициента жесткости горизонтального шва ξ.

Способ осуществляется следующим образом. Для заданной двухслойной конструкции балочного типа с известными физическими и геометрическими характеристиками каждого из ее слоев вычисляют физико-геометрические параметры, входящие в выражение (14): E₀I₀ - по формуле (5), 1/D - по формуле (8) и γ - по формуле (4). В шарнирно опертой по концам конструкции, установленной на стенде или стоящей в сооружении, с помощью механического удара или внезапного снятия нагрузки возбуждают собственные поперечные колебания на основной частоте (или вынужденные колебания на первой резонансной частоте) и измеряют эту частоту колебаний f. Подставляя значение этой частоты в формулу (14), находят методом последовательных приближений значение параметра λ, а затем из выражения (3) - значение коэффициента жесткости горизонтального шва ξ.

Примеры реализации способа

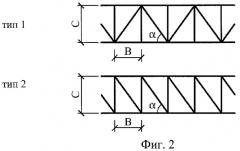
Численный эксперимент. В качестве модели двухслойной составной шарнирно опертой балки можно использовать стальную шарнирно опертую по концам ферму с параллельными поясами и регулярной решеткой (фиг.3). Поскольку для некоторых типов регулярной решетки таких ферм (см. фиг.2) в учебной литературе [1, с.18-21] приводятся точные формулы для подсчета коэффициента жесткости решетки (что равносильно коэффициенту жесткости шва в балке), а определение основной частоты колебаний фермы, нагруженной в ее узлах сосредоточенными массами от собственного веса фермы, является элементарной задачей строительной механики, то для тестирования предлагаемого способа можно использовать численный эксперимент, выполнив аналитический расчет указанных типов ферм.

Рассмотрим однопролетные шарнирно опертые по концам стальные фермы с параллельными поясами и регулярной решеткой (фиг.2). Длина ферм L=2l=12,0 м, высота с=1,5 м, длина панели В переменная от 0,5 до 2,0 м с шагом 0,5 м (по четыре фермы каждого типа); элементы верхнего и нижнего поясов выполнены из стальных труб 180×6 мм (E₁=E₂=2×10⁵ МПа, A₁=А₂=16,68 см², I₁=I₂=653,47 см⁴), а элементы решетки - из труб 140×6 мм (А_р=А_с=12,91 см², где А_р и A_c - площади поперечных сечений элементов решетки и стоек соответственно); погонные массы ферм m₁=89,18 кг/м, m₂=60,04 кг/м, m₃=52,24 кг/м, m₄=48,03 кг/м. Требуется определить коэффициент жесткости решетки (коэффициент жесткости шва составной конструкции) с использованием предложенного способа.

Расчет фермы для определения основной частоты колебаний выполнялся на ЭВМ с использованием программного комплекса «SCAD». Значения коэффициентов жесткости шва ξ подсчитывались путем последовательных приближений из уравнения (13) и по точным формулам А.Р.Ржаницына [1, с.19-20]:

- для решетки первого типа

- для решетки второго типа

Результаты расчета и сопоставления коэффициентов ξ сведены в таблицу 1.

Таблица 1
Определение коэффициента жесткости решетки стальных ферм с параллельными поясами с помощью численного эксперимента
Тип решетки фермы	Длина панели В, м	Основная частота колебаний, определенная расчетом с помощью «SCAD», c-1	Коэффициент ξ, подсчитанный по формуле (14), Па	Коэффициент ξ, подсчитанный по формулам (15) и (16), Па	Разница, %
1	0,5	123,15	8,672×107	8,543×107	1,51
1,0	154,73	11,790×107	11,530×107	2,25
1,5	165,32	10,340×107	10,610×107	2,54
2,0	166,96	8,144×107	8,645×107	5,79
2	0,5	111,46	4,594×107	4,608×107	0,30
1,0	146,48	7,415×107	7,314×107	1,38
1,5	159,60	7,744×107	7,840×107	1,22
2,0	162,99	6,686×107	7,109×107	5,95

Анализ приведенных в таблице 1 результатов позволяет сделать следующие выводы:

- с помощью предложенного способа можно с удовлетворительной точностью определять значение коэффициента жесткости регулярной решетки ферм с параллельными поясами (горизонтального шва составных балок);

- чем меньше длина панели В (чем чаще расположены поперечные связи в составной балке), тем выше точность предложенного способа; на этом основании предлагаемый способ рекомендуется использовать для ферм с углом α≥35,0°.

Пример натурного эксперимента. Для натурного эксперимента были изготовлены две модели стальных ферм, отличающихся конфигурацией решетки (фиг.4): пролет ферм 2l=3,0 м, высота с=0,5 м; верхний и нижний пояса выполнены из спаренных уголков 25×4 мм по ГОСТ 8509-93 (E₁=E₂=2×10⁵ МПа, A₁=A₂=3,72 см, I₁=I₂=2,06 см⁴), а элементы решетки - из арматурных стержней ⌀8A-III по ГОСТ 5781-82 (А_с=А_р=0,322 см²); погонная масса ферм m₁=m₂=7,09 кг/м.

В процессе динамических испытаний свободные поперечные колебания в ферме возбуждались с помощью механического удара в ее средней части, а частоту основного тона установившихся свободных колебаний определяли с помощью электронного прибора - виброанализатора «Вибран-2», вибродатчик от которого закреплялся также на верхнем поясе фермы в ее средней части (фиг.5). Результаты измерений частоты колебаний после их статистической обработки приведены в таблице 2 (колонка 2). В колонках 3 и 4 представлены результаты аналитических расчетов, а в колонке 5 - результаты сопоставления точных значений ξ со значениями, полученными с помощью предлагаемого способа.

Таблица 2
Сопоставление произведения W0ω2 для моделей ферм
Тип решетки фермы (фиг.2)	Основная частота колебаний ω, Гц	Значения параметра ξ, Па	Разница, %
по формулам (14) и (15)	по предложенному способу
1	105,00	1,622×107	1,529×107	-5,73
2	90,50	1,073×107	1,017×107	-5,21

Полученные отклонения находятся в пределах 6%, что свидетельствует о работоспособности предлагаемого способа определения жесткости горизонтального шва составной конструкции балочного типа.

Таким образом, в предложенном способе определения жесткости горизонтального шва двухслойной конструкции балочного типа технический результат - расширение технологических возможностей способа для применения его к длинномерным конструкциям, в том числе стоящим в сооружении, и снижение трудоемкости реализации способа - достигаются за счет замены статического сдвигового нагружения фрагмента балки по шву возбуждением в шарнирно опертой по концам балки собственных поперечных колебаний на основной частоте (или первой резонансной частоте) и измерении этой частоты.

Источники информации

1. Ржаницын А.Р. Составные стержни и пластинки. - М.: Стройиздат, 1986. - 316 с.

2. Коробко В.И., Коробко А.В. Строительная механика: Динамика и устойчивость стержневых систем. - М.: Изд-во АСВ, 2008. - 400 с.

Способ определения коэффициента жесткости горизонтального шва двухслойной конструкции балочного типа, заключающийся в установке и закреплении конструкции на стенде, нагружении ее, измерении физических параметров, характеризующих деформированное состояние конструкции, и аналитическом вычислении коэффициента жесткости горизонтального шва, отличающийся тем, что в шарнирно опертой по концам конструкции с помощью механического удара или внезапного снятия нагрузки возбуждают собственные поперечные колебания на основной частоте или вынужденные колебания на первой резонансной частоте, измеряют соответствующую частоту, вычисляют значение параметра λ из уравнения где m - погонная масса балки,l - пролет балки, где E_i - модуль упругости материала,A_i, I_i - площадь поперечного сечения и момент инерции каждого слоя балки соответственно,с - расстояние между центрами тяжести слоев составной балки,а по параметру λ вычисляют значение коэффициента жесткости горизонтального шва из выражения ξ=λ²/γ,где