Способ калибровки бесплатформенных инерциальных навигационных систем

Способ калибровки бесплатформенных инерциальных навигационных систем

Иллюстрации

Показать все

Реферат

Изобретение относится к навигационному приборостроению и может быть применено при калибровке бесплатформенных инерциальных систем ориентации и навигации в процессе лабораторных, заводских и приемосдаточных испытаний.

Известны способы калибровки гироскопов и акселерометров на двухосных калибровочных наклонно-поворотных столах (US 3736791, 1973; GB 1094396, 1964; RU 2044272, 1995; SU 1820219, 1993; RU 2121134, 1998; RU 98112966, 1998). Наиболее близким по технической сущности является способ определения коэффициентов модели инструментальных погрешностей навигационной системы (RU 98112966, 1998), использующий независимые суммарные погрешности навигационной системы, полученные путем вычитания из значений ускорений и угловых скоростей инерциальных измерителей значений ускорений и угловых скоростей, полученных независимым путем.

Сравнительный анализ с прототипом показал, что заявляемое изобретение отличается тем, что в нем для определения калибровочных коэффициентов инерциальных измерителей используется полный вектор измерения ошибок БИНС, а не ошибки измерения только ускорений и угловых скоростей акселерометрами и датчиками угловых скоростей (ДУСами), кроме того, система работает при калибровке в автономном (основном) режиме.

Техническим результатом изобретения является повышение точности калибровки инерциальных измерителей и точности работы БИНС.

Указанный технический результат достигается тем, что в процессе калибровки БИНС работает в автономном режиме, тем самым более полно учитываются не только инструментальные погрешности измерителей, но и снижается влияние принятых приближений при разработке бортового программного обеспечения БИНС.

Рассмотрим пример реализации предлагаемого способа калибровки на примере двухканальной БИНС, в которой в качестве ДУСов применяются волоконно-оптические гироскопы (ВОГи), модель ошибок которых примем в виде:

где - векторы шумов ВОГов; ω_ni - ошибки типа «смещения» нуля соответствующих ВОГов; - матрица углов перекосов осей чувствительности ВОГов; ω_x,y,z - проекции угловой скорости суточного вращения Земли; Δk_d - диагональная матрица ошибок масштабных коэффициентов ВОГов, имеющая вид:

Матрица углов перекосов осей чувствительности ВОГов равна:

где ν_ij - углы перекосов осей чувствительности ВОГов.

Модель ошибок акселерометров БИНС примем в виде:

где f_n,i - ошибки типа «смещения» нуля акселерометров; - матрица углов перекосов осей чувствительности акселерометров:

где µ_ij - углы перекосов осей чувствительности акселерометров; f_i - проекции ускорения силы тяжести; - векторы шумов акселерометров; Δk_a - диагональная матрица масштабных коэффициентов акселерометров, имеющая вид:

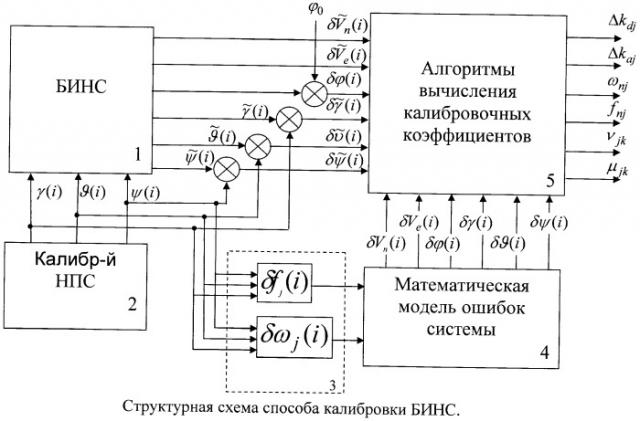
Структурная схема способа калибровки БИНС с использованием математической модели ошибок системы представлена на чертеже. На схеме блок 1 представляет калибруемую БИНС, которая установлена на калибровочном наклонно-поворотном столе (блок 2). В блоке 3 определяются векторы ошибок ВОГов и акселерометров δω_j(i), δf_j(i) в соответствии с i-й ориентацией калибровочного НПС. В блоке 4 формируются математические модели ошибок БИНС в «i» ориентации НПС и их аналитические решения δV_n(i), δϑ(i), δψ(i), δV_e(i), δγ(i), δφ(i). В блоке 5 формируются алгоритмы вычисления калибровочных коэффициентов инерциальных измерителей. Калибровочные коэффициенты определяются в два этапа. На первом этапе формируются алгебраические уравнения:

для определения входных сигналов математической модели ошибок северного канала δω_n(i), δf_n(i) и входных сигналов математической модели ошибок восточного канала δω_e(i), δf_e(i), которые являются функциями ошибок инерциальных измерителей и калибровочных сигналов в i-й ориентации калибровочного НПС. На втором этапе по алгебраическим суммам входных сигналов математических моделей ошибок северного и восточного каналов БИНС определяются калибровочные коэффициенты инерциальных измерителей.

Аналитические решения δV_n(i), δϑ(i), δV_e(i), δγ(i), представленные в выражениях (7), получим для самого простого варианта модели ошибок БИНС:

Системы дифференциальных уравнений (8) и (9) описывают ошибки северного и восточного каналов двухканальной БИНС. Они получены с использованием упрощений, заключающихся в том, что пренебрегли перекрестными связями между каналами, которые приводят к появлению в решениях членов, представляющих суточные колебания с периодами близкими 24 часам. Аналитические решения систем (8) и (9) тогда включают только шулеровские колебания с периодами 84,4 минуты:

где ω_s=1,24·10^-3 с^-1 - частота шулеровских колбаний.

Упрощения можно сделать в силу того, что при калибровке время работы БИНС в каждой ориентации калибровочного НПС не превышает 2-3 минут. В этом случае алгебраические уравнения (7) для i-й ориентации калибровочного НПС можно представить в виде:

где коэффициенты и имеют конкретные числовые значения на момент времени t=Δt·l, l=0, 1, 2, …; i - номер ориентации; R-радиус Земли. Решив эти системы уравнений методом Крамера, получим выражения для определения входных сигналов модели ошибок БИНС:

Определением входных сигналов модели ошибок БИНС заканчивается первый этап. На втором этапе по выражениям (12) определяем значения калибровочных коэффициентов инерциальных измерителей. Калибровочные коэффициенты определяются по уравнениям:

в уравнениях (13) в левых частях стоят алгебраические суммы аналитических входных сигналов модели ошибок БИНС, определенные в соответствии с принятыми моделями ошибок инерциальных измерителей, для различных ориентации калибровочного НПС, а в правых частях алгебраические суммы рассчитанных входных сигналов для тех же условий.

Введем восемь ориентации калибровочного НПС в соответствии с таблицей.

№ ориентации	Углы положения калибровочного НПС относительно системы координат с географической ориентацией осей
1	ψ=0°; ϑ=0°; γ=45°.
2	ψ=90°; ϑ=45°; γ=0°.
3	ψ=180°; ϑ=0°; γ=315°.
4	ψ=270°; ϑ=315°; γ=0°.
5	ψ=0°; ϑ=0°; γ=225°.
6	ψ=90°; ϑ=45°; γ=180°.
7	ψ=180°; ϑ=0°; γ=135°.
8	ψ=90°; ϑ=225°; γ=0°.

Для указанных в таблице ориентаций калибровочного НПС можно сформировать определения калибровочных коэффициентов ВОГа, установленного по оси ОХ БИНС, совпадающей с продольной осью объекта, четыре алгебраических уравнения, по числу неизвестных калибровочных коэффициентов эти уравнения соответствуют первому уравнению системы (13):

Решив систему (14), получим выражения для определения калибровочных коэффициентов ВОГа, установленного по оси ОХ:

;

Для ВОГов, установленных по осям OY и OZ, для определения их калибровочных коэффициентов можно сформировать аналогичные уравнения для указанных выше ориентаций калибровочного НПС.

Для определения калибровочных коэффициентов акселерометров используется второе уравнение системы (13) по аналогичной методике. Так калибровочные коэффициенты акселерометра, установленного по оси ОХ, определяются по следующим выражениям:

Калибровочные коэффициенты акселерометров, установленных по осям OY и OZ, определяются по аналогичной методике.

Способ определения коэффициентов модели ошибок бесплатформенной инерциальной навигационной системы, основанный на осуществлении с помощью калибровочного стола последовательности поворотов системы в требуемые фиксированные положения, вычислении калибровочных коэффициентов, отличающийся тем, что калибровочные коэффициенты инерциальных измерителей навигационной системы определяются в два этапа: на первом этапе по составляющим вектора ошибок системы, полученным по показаниям системы, показаниям калибровочного стола и значениям широты места установки калибровочного стола, определяются входные сигналы модели ошибок навигационной системы, являющиеся функциями калибровочных коэффициентов, на втором этапе по входным сигналам модели ошибок системы вычисляются калибровочные коэффициенты инерциальных измерителей.