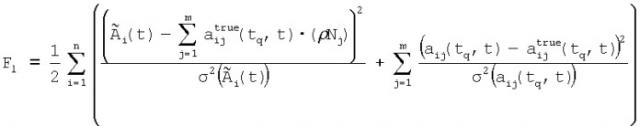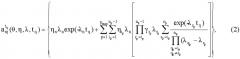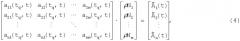Способ идентификации ядерного взрыва по изотопам криптона и ксенона

Способ идентификации ядерного взрыва по изотопам криптона и ксенона

Иллюстрации

Показать все

Реферат

Область техники

Изобретение относится к ядерной физике и может быть использовано в системах идентификации источников радиоактивности в атмосфере.

Уровень техники

Идентификация ядерных взрывов по изотопам радиоактивных благородных газов (РБГ) имеет место в процессе мониторинга радиоактивной обстановки для осуществления контроля по соблюдению Договора о Всеобъемлющем запрещении ядерных испытаний (ДВЗЯИ).

Известны способы идентификации ядерных взрывов по радиоактивным изотопам криптона и ксенона:

I. Метод, разработанный в СССР в конце 60-х гг. Схема измерения активности РБГ заключается в следующем [1]: в атмосфере отбирается проба (после события), которая исследуется в течение некоторого времени. На протяжении всего этого времени проводится измерение активности изотопов криптона и ксенона однокристальным сцинтилляционным γ-спектрометром NaJ(Tl).

Измеренные активности изотопов криптона и ксенона служат для формирования системы линейных алгебраических уравнений (СЛАУ) относительно неизвестных вкладов источников РБГ в суммарную активность изотопов криптона и ксенона. Система уравнений решалась с помощью метода наименьших квадратов (МНК).

II. Это усовершенствованный подход [2] изложенного методе I, который позволяет устранить некоторые его недостатки - учесть погрешности элементов матрицы решаемой системы уравнений и обеспечить получение устойчивого решения путем применения метода регуляризации А.Н.Тихонова (2003 г).

Ближайшим аналогом предлагаемого способа является метод, описанный в п.II, при котором:

1. Измеряют в атмосфере активности отдельных изотопов криптона и ксенона (t - момент измерения), где , n - число измеряемых изотопов.

2. Для различных видов делящегося материала (под видом деления понимается один из вариантов деления тяжелых ядер урана 235, урана 238, плутония 239 нейтронами спектра деления или нейтронами с энергией 14 МэВ) по отношениям активностей изотопов криптона и ксенона, построенных с учетом и без учета сепарации, определяют интервал времени [t_H, t_K], на котором произошла сепарация.

3. На интервале [t_H, t_K] задают сетку времени с шагом Δt.

4. Для каждого узла сетки t_q формируют и запоминают двумерный сигнал , , удельных активностей изотопов криптона и ксенона, в котором строки соответствуют конкретному изотопу, а столбцы - конкретному виду деления; n - число рассматриваемых изотопов; m - число рассматриваемых видов деления; t - момент измерения пробы; t_q - предполагаемый момент сепарации.

5. Считая измеренные значения активностей и элементы двумерного сигнала статистически независимыми величинами, распределенными по нормальному закону со среднеквадратическими отклонениями и соответственно, при заданном времени t_q формируют одномерный сигнал:

,

где (ρN_j), - подлежащие определению вклады источников радиоактивности в суммарную активность; - неизвестные истинные значения удельных активностей, a_ij(t_q,t) - удельные активности, рассчитанные по имеющим погрешности независимым и кумулятивным выходам элементов изобарных цепочек радиоактивных превращений (ИЦРП); l - номер итерации поиска оценок и .

6. Задают числа γ₁, γ₂, характеризующие точность оценок и .

7. Итеративно находят минимум сигнала F_l по ρN_j и , используя регуляризацию А.Н.Тихонова и соблюдая выполнение ограничений , i=1, 2, …, n, j=1, 2, …, m, до выполнения условий:

,

где индекс (l-1) обозначает значение, полученное на предыдущей итерации.

8. Ковариационная матрица оценок определяется соотношением

i, j=1, 2, …, m.

Недостатки аналога следующие:

1) используется только регуляризация Тихонова, что требует дополнительного определения параметра регуляризации, однозначного метода определения которого не существует; причем регуляризация Тихонова «сглаживает» решение, что может привести к большим ошибкам в идентификации;

2) рассматриваемая система уравнений переопределенная, т.е. число строк двумерного сигнала больше числа столбцов - число уравнений больше числа неизвестных. Возможность применения данного подхода в реальных ситуациях, когда измерение радиоактивности изотопов криптона и ксенона проводится через несколько дней после события и когда число неизвестных ρN_j (вкладов различных источников) больше числа измеряемых изотопов, т.е. количества величин , не исследовалась.

Тем самым, аналог не обеспечивает идентификацию ядерного взрыва в наиболее вероятном случае, когда измеряется активность от 2-х до 4-х изотопов, а отбор проб проводится через 5-6 суток после события. Указанные недостатки, очевидно, не позволят применять способ в реальных условиях из-за его низкой практической эффективности.

Раскрытие изобретения

Техническим результатом предлагаемого способа является повышение достоверности определения факта проведенного ядерного взрыва при измеряемом числе изотопов, меньшем, чем рассматриваемое число неизвестных (видов деления). Эффективность предлагаемого способа обеспечивается за счет:

1) одновременного рассмотрения разных предполагаемых комбинаций источников активности изотопов криптона и ксенона и о различных механизмах ядерного взрыва;

2) разработки и включения в способ идентификации ядерного взрыва аппарата многокритериального математического программирования, позволяющего учесть всевозможные виды дополнительных условий (неотрицательность решения, ограниченность решения), которым должна удовлетворять оценка решения, и не требующие определения параметра регуляризации (по А.Н.Тихонову), четко формализованных процедур определения которого не существует;

3) объединения двух видов деления урана 235 нейтронами спектра деления и нейтронами с энергией 14 МэВ в один вид деления, а также двух видов деления плутония 239 нейтронами спектра деления и нейтронами с энергией 14 МэВ в один вид деления путем усреднения независимых и кумулятивных выходов элементов ИЦРП.

Способ идентификации ядерного взрыва по изотопам криптона и ксенона характеризуется измерением в атмосфере активности отдельных изотопов криптона и ксенона (Kr^83m, Kr^85m, Kr⁸⁵, Kr⁸⁸, Xe^131m, Xe^133m, Xe¹³³, Xe¹³⁵), где , n - число измеряемых изотопов; построением для различных видов делящегося материала зависимостей отношения активностей изотопов (например, Kr^85m/Xe¹³⁵) от времени без сепарации в интервале от момента возникновения события (ядерного взрыва) до момента измерения активностей изотопов криптона и ксенона; расчетом из измеренных экспериментальных точек в «обратном времени» отношения изотопов до совпадения их значений со значениями относительной активности без учета сепарации; определением по совпадению «экспериментальных» значений с «теоретическими» интервала времени [t_H, t_K], на котором, возможно, произошла сепарация изотопов криптона и ксенона от их предшественников по ИЦРП; формированием на интервале [t_H, t_K] сетки времени с шагом Δt, формированием и запоминанием для каждого узла сетки t_q двумерного сигнала удельных активностей изотопов криптона и ксенона , , ; формированием при условии, что измеренные значения активностей и элементы двумерного сигнала являются статистически независимыми величинами, распределенными по нормальному закону с математическими ожиданиями и и среднеквадратическими отклонениями и соответственно, для определенного момента сепарации t_q одномерного сигнала F_l; указанием малых чисел γ₁, γ₂ - допускаемых величин ошибок; формированием двумерного сигнала удельных активностей , , одновременно для разных комбинаций источников радиоактивности и различных механизмов ядерного взрыва. Определение оценки вкладов активностей отдельных источников осуществляют посредством формирования нескольких целевых функций и использованием методов многокритериального математического программирования, сведением многокритериальной задачи к однокритериальной задаче с ограничениями, получением итерационными вычислительными процедурами решения указанной однокритериальной задачи с ограничениями, определением по значениям (числа делений j-го вида) вклада каждого источника в суммарную активность, т.е. идентификация параметров ядерного взрыва. В процессе решения за истинную принимается комбинация источников изотопов РБГ, дающая минимальное значение сигнала F_l.

Для определения факта ядерного взрыва по малому числу измеренных изотопов, два вида деления урана 235 (деление нейтронами спектра деления и нейтронами с энергией 14 МэВ) объединяются в один вид деления и два вида деления плутония 239 (деление нейтронами спектра деления и нейтронами с энергией 14 МэВ) объединяются в один вид деления посредством усреднения соответствующих указанным видам деления независимых и кумулятивных выходов элементов ИЦРП.

Перечень фигур.

Фиг.1 - изменение относительной активности изотопов A(Xe133m)/A(Xe133) в случае деления и без сепарации (сплошная и штриховая линии, соответственно) и с учетом сепарации от предшествующих изотопов (линия с маркерами), точка 1 - это отношение измеренных активностей изотопов в момент времени t=12 часов.

Фиг.2 - общая блок-схема алгоритма получения оценок момента сепарации и решения

Фиг.3 - блок-схема алгоритма решения плохо обусловленной системы линейных алгебраических уравнений с помощью конфлюэнтного анализа (соответствует блоку 1 Фиг.2 общей блок-схемы).

Фиг.4 - график зависимости кумулятивных выходов изотопов Xe¹³³ и Xe¹³⁵ от относительного вклада нейтронов спектра деления и нейтронов энергии 14 МэВ.

Осуществление изобретения

Необходимо определить следующие параметры источников ядерного взрыва по РГБ в атмосфере: вклады каждого вида деления (делящегося материала и энергии нейтронов ) в суммарную активность РБГ, измеренную в атмосфере.

В качестве практически оправданного допущения для предлагаемого способа регистрируемые сигналы (активности изотопов) рассматривают как детерминированные, подверженные аддитивной помехе, оценки параметров которых подлежат определению.

При мгновенном делении i-й изотоп появляется в результате различных видов деления, и его измеренная активность выражается следующим образом [3]:

где a_ij(θ, η, λ, t, t_q) - активность i-го изотопа при j-м виде деления для одного акта распада, вычисленная с учетом сепарации на момент времени t>t_q, т.е. удельная активность; θ - вектор параметров, характеризующих сепарацию измеряемых изотопов от предшествующих им; η - вектор независимых выходов изотопов (при j-м виде деления); λ - вектор постоянных распада; t - время наблюдения; t_q - предполагаемый момент сепарации изотопов криптона и ксенона от предшествующих им изотопов по цепочкам радиоактивных превращений; ρ - доля i-го изотопа в образце (значение ρ обычно неизвестно); N_j - число делений j-го вида.

До момента сепарации t_q удельная активность определяется формулой:

где

η_i - независимый выход i-го изотопа;

n_p - номер исследуемого изотопа по p-й ветви;

n - максимальный член из {n_p};

p_max - число ветвей цепочки;

(n_p-1) - число изотопов, предшествующих исследуемому по p-й ветви распада;

- доля r-го члена цепочки, получающегося из (r-1)-го по p-й ветви;

, , , - постоянные распада изотопов, имеющих соответственно номера i_p, r_p, s_p, q_p по p-й ветви, причем i_p≤r_p≤n_p-1; i_p≤s_p≤n_p; i_p≤q_p≤n_p и q_p≠s_p;

t_q - время, когда произошло мгновенное отделение исследуемого изотопа от предшественников, после чего распад изотопа идет по экспоненте с постоянной распада λ_n.

После момента сепарации изотопы распадаются по своим постоянным распада λ_i:

где - удельная активность, рассчитанная по формуле (2) на момент времени t_q.

Уравнения вида (1) составляются для каждого измеряемого изотопа криптона и ксенона, в результате формируется СЛАУ

в которой определению подлежат неизвестные вклады источников радиоактивности ρN_j в суммарную активность изотопов криптона и ксенона.

Первый этап решения задачи идентификации источников РГБ - определение времени сепарации t_q изотопов криптона и ксенона. Временной отрезок, которому принадлежит момент сепарации, можно найти, «достроив» относительные активности изотопов в различных видах деления «в обратном времени» от момента измерения без учета влияния предшествующих им изотопов и определив точки пересечения линий, проведенных из экспериментальных точек, с относительными активностями, построенными с учетом влияния предшествующих изотопов по цепочке распада изотопов.

На Фиг.1 приведены графики относительной активности для двух изотопов ксенона (Xe^133m, Xe¹³⁵), экспериментальная точка 1 соответствует моменту измерения активностей t=12 часов после события. Чтобы не усложнять чертеж, изображены только «граничные» линии, соответствующие и (вместо 6 возможных видов деления: , , , , и ). Как видно из Фиг.1, момент сепарации принадлежит интервалу от t_H=3 до t_K=4 часов после события.

Задавая сетку времени внутри отрезка [t_H, t_K] и решая систему (4) для моментов t_q, соответствующих узлам сетки, в качестве момента сепарации принимают время , для которого сумма квадратов невязок системы (4) минимальна. Общая схема алгоритма, позволяющего найти оценки , , приведена на Фиг.2.

Второй этап решения задачи идентификации ядерного взрыва - определение для каждого фиксированного момента сепарации t_q оценок решения При заданном t_q система (4) является линейной относительно неизвестных j=1, 2, …, m. Поскольку элементы двумерного сигнала не могут быть точно рассчитаны (независимые выходы известны с погрешностями) и активности изотопов также измеряются с ошибками, будем считать, что элементы двумерного сигнала А и измеренные активности - независимые случайные величины, распределенные по нормальному закону с математическими ожиданиями, равными и , и дисперсиями, равными и , соответственно:

где , - истинные значения удельных и измеренных активностей изотопов (которые нам неизвестны); ε_ij - погрешности определения удельных активностей a_ij(t_q, t); δ_i - ошибки измерения активностей РБГ в атмосфере.

Для учета погрешностей как в измеренных активностях , так и в элементах двумерного сигнала используется определение ортогональной регрессии [4] и в силу независимости случайных величин и можно записать сигнал:

где (ρN_j), - подлежащие определению вклады источников радиоактивности в суммарную активность; - неизвестные точные значения удельных активностей, оценки которых определяются в процессе нахождения ρN_j, - удельные активности, рассчитанные по формулам (2)-(3) по имеющим погрешности независимым и кумулятивным выходам элементов изобарных цепочек радиоактивных превращений; - измеренные в пробе активности РБГ.

В сигнале (6) наряду с неизвестным вектором вкладов источников радиоактивности ρN_j, j=1, 2, …, m, неизвестными также являются истинные значения вычисляемых активностей , i=1, 2, …, n, j=1, 2, …, m, для поиска оценок которых используется конфлюэнтный анализ [3, 4].

В точке минимума сигнала (6) должны выполняться условия:

Структурная схема поиска минимума сигнала (6) приведена на Фиг.3 - она соответствует блоку 1 структурной схемы Фиг.2.

Несмотря на линейность при фиксированном t_q систем уравнений (7)-(8), задача является вычислительно некорректной в силу плохой обусловленности системы (7). Отношение максимального и минимального собственных чисел матрицы системы (7) достигает порядка 10. Поэтому для ее решения необходимо применение специфических методов, в предлагаемом способе это методы многокритериального математического программирования, в которых не требуется определять значение параметра регуляризации, как в других методах решения некорректных задач.

На первом шаге при решают СЛАУ (7) методами многокритериального математического программирования (метод сжатия области допустимых значений, целевой программирование) и находят первое приближение оценки

Для получения оценок истинных значений при заданном значении t_q на каждом шаге получения оценок j=1, 2, …, m, используется условие (8) [3], что приводит к решению дополнительно n систем линейных уравнений с m неизвестными следующего вида:

i=1, 2, …, n, v=1, 2, …, m.

Полученные оценки значений должны удовлетворять естественному условию, то есть принадлежать области неопределенности измеренных значений :

, i=1, 2, …, n, j=1, 2, …, m,

Если это условие не выполняется, то , j=1, 2, …, m, которые не удовлетворяют этому неравенству, следует заменить на значения ближайших граничных точек. Из-за этого может происходить увеличение значений функционала F_l на новых точных значениях переменных по сравнению с предыдущим шагом итерационного процесса, что приводит к снижению скорости сходимости итерационного процесса или к возникновению колебаний. Чтобы значения функционала не увеличивались после пересчета оценок , j=1,2 …, m, те наборы оценок , j=1, 2, …, m, для которых произошло увеличение соответствующих слагаемых функционала F_l по сравнению с их значениями на предыдущей итерации, следует заменить на соответствующие значения для предыдущего шага.

После определения оценок истинных значений находят очередное приближение к решению ρN_j, j=1, 2, …, m методами многокритериального математического программирования вместо регуляризации А.Н.Тихонова, как это делается в аналоге.

Критерием останова алгоритма является несущественное различие значений функционала F_l и компонентов вектора ρN_j на соседних итерациях, т.е. выполнение неравенств

где - очередное приближение к решению на l-й итерации; γ₁, γ₂ - некоторые числа (малые десятичные дроби, например, 0,001), определяющие точность вычисления значений оценок

При решении методами многокритериального математического программирования:

1) Формируют двухкритериальную задачу математического программирования:

при ограничениях ρN_j≥0, .

2) Используя метод пороговой оптимизации или целевое программирование, от двухкритериальной задачи математического программирования (10) переходят к однокритериальной задаче посредством перевода всех, кроме одного, из вышеуказанных функционалов в условия ограничений.

Метод пороговой оптимизации (или метод e-ограничений) приводит к различным возможным комбинациям целевых функций и ограничений. В алгоритме используют следующие их виды:

Задача (11) является задачей квадратичного программирования, задача (12) - задачей нелинейного программирования.

Оценки правых частей ограничений δ и β могут быть получены при независимой минимизации функционалов J₁ и J₂ при ограничениях ρN_j≥0, . При этом может использоваться любой из методов математического программирования.

В целевом программировании существует две модели решения - архимедова и модель с приоритетами.

При использовании архимедовой модели все целевые функции переводят в ограничения и осуществляют минимизацию взвешенной суммы меры их отклонений от ограничений:

где w_i - весовые коэффициенты. ; d_i - отклонения от ограничений.

В модели с приоритетами осуществляют последовательный перевод целевых функций в ограничения и минимизацию отклонения значений целевых функций от ограничений. При этом найденное на данном шаге значение отклонения d_i используют как оптимальное отклонение на следующем i+1 шаге:

При идентификации ядерного взрыва по малому числу изотопов ксенона используется тот факт, что выход этих изотопов слабо зависит от энергии нейтронов. Это иллюстрирует Фиг.4, на которой представлены графики усредненных кумулятивных выходов изотопов Xe¹³³ и Xe¹³⁵ в зависимости от долей кумулятивных выходов, соответствующих нейтронам спектра деления и нейтронам с энергией 14 МэВ. Кумулятивные выходы известны с погрешностями до 5%. Из Фиг.4 видно, что усредненные значения выходов (для примера приведены значения, соответствующие равным долям нейтронам спектра деления и нейтронам с энергией 14 МэВ) укладываются в эти погрешности.

Для идентификации по 2…4 измеренным изотопам применяют объединения двух видов деления урана 235 (нейтронами спектра деления и нейтронами с энергией 14 МэВ) в один вид деления и двух видов деления плутония 239 (нейтронами спектра деления и нейтронами с энергией 14 МэВ) в один вид деления, что приводит к сокращению числа идентифицируемых видов деления (вместо четырех рассматривается два).

При этом удельную активность рассчитывают

1) для делящегося материала урана 235 по формуле (2) с вектором независимых выходов , где и - независимые выходы элементов изобарных цепочек при делении урана 235 нейтронами спектра деления и нейтронами с энергией 14 МэВ, соответственно; c₁ - параметр, учитывающий доли независимых выходов и в их сумме, c₁∈[0,1];

2) для делящегося материала плутония 239 по формуле (2) с вектором независимых выходов , где и - независимые выходы элементов изобарных цепочек при делении плутония 239 нейтронами спектра деления и нейтронами с энергией 14 МэВ, соответственно; c₂ - параметр, учитывающий доли независимых выходов и в их сумме, c₂∈[0,1].

Задавая по c₁ и c₂ двумерную сетку с шагом Δc₁ и Δc₂, соответственно, и находя минимум сигнала (6) для разных c₁ и c₂, за истинные вклады источников и в суммарную активность изотопов криптона и ксенона принимают те, при которых сумма квадратов невязок системы (2) минимальна.

Таким образом, предлагаемый способ идентификации параметров ядерного взрыва осуществляют следующим образом:

1. Измеряют в атмосфере активности отдельных изотопов криптона и ксенона (Kr^83m, Kr^85m, Kr⁸⁵, Kr⁸⁸, Xe^131m, Xe^133m, Xe¹³³, Xe¹³⁵) (t - момент измерения), где , n - число измеряемых изотопов.

2. Для различных видов делящегося материала (,,,) строят зависимости отношения активностей изотопов (например, Kr^85m/Xe¹³⁵) от времени без учета сепарации в интервале от момента возникновения события (ядерного взрыва) до момента измерения активностей изотопов криптона и ксенона.

3. Из измеренных экспериментальных точек определяют в «обратном времени» отношения изотопов (например, Kr^85m/Xe¹³⁵) до их совпадения со значениями относительной активности этих же изотопов без учета сепарации.

4. По совпадению значений определяют интервал времени [t_H, t_K] на котором произошла сепарация изотопов криптона и ксенона от их предшественников по изобарным цепочкам радиоактивных превращений.

5. На интервале [t_H, t_K] задают сетку по времени с шагом Δt.

6. Для каждого узла сетки t_q формируют и запоминают двумерный сигнал удельных активностей изотопов криптона и ксенона

,

в котором строки соответствуют конкретному изотопу, а столбцы - конкретному виду деления; m - число рассматриваемых видов деления. При этом a_ij(t) соответствует значению удельной активности i-го изотопа для j-го вида деления, рассчитанной до момента сепарации t_q по формуле (2), a - рассчитанной на момент времени t, превышающий момент сепарации t_q по формуле (3).

7. Считая, что измеренные значения активностей и элементы двумерного сигнала являются статистически независимыми величинами, распределенными по нормальному закону с математическими ожиданиями и и среднеквадратическими отклонениями и соответственно, формируют по формуле (6) одномерный сигнал F_l.

8. Задают числа γ₁, γ₂, характеризующие точность оценивания и .

9. На первой итерации, принимая (а на последующих итерациях формируют двухкритериальную задачу математического программирования.

при ограничениях ρN_j≥0, .

10. Используя метод сжатия области допустимых значений или целевое программирование, от двухкритериальной задачи математического программирования по формулам (11)-(14) переходят к однокритериальной задаче посредством перевода всех, кроме одного, из вышеуказанных функционалов в условия-ограничения.

11. Методами квадратичного программирования, нелинейного программирования, целевого программирования (архимедова модель и модель с приоритетами) находят первое приближение оценки вкладов активностей отдельных источников в суммарную активность.

12. Получив первое приближение уточняют элементы двумерного сигнала . Для этого дополнительно решают n систем линейных уравнений с m неизвестными вида:

куда вместо i=1, 2, …, n, v=1, 2, …, m,

(ρN_j) подставляют приближение оценки найденное на первой итерации.

13. Проверяют, удовлетворяют ли новые значения естественной области неопределенности элементов :

, i=1, 2, …, n, j=1, 2, …, m.

Если это условие не выполняется, то , j=1, 2, …, m, которые не удовлетворяют этому неравенству, заменяют на значения ближайших граничных точек. Из-за этого может происходить увеличение значений сигнала F_l на новых значениях переменных по сравнению с предыдущим шагом итерационного процесса, что приводит к снижению скорости сходимости итерационного процесса и возникновению колебаний. Чтобы значения сигнала F_l не увеличивались после пересчета оценок , j=1, 2, …, m, те наборы оценок , j=1, 2, …, m, для которых происходит увеличение соответствующих слагаемых сигнала F_l по сравнению с их значениями на предыдущей итерации, заменяются на соответствующие значения для предыдущего шага.

14. Операции, перечисленные в пп.9-13, повторяются до тех пор, пока не будут выполнены условия:

15. Для идентификации ядерного взрыва по малому числу изотопов (2…4 изотопа) задают двумерную сетку по c₁ и c₂ с шагом Δc₁ и Δc₂, соответственно, где c₁ и c₂ веса для суммирования независимых и кумулятивных выходов элементов ИЦРП.

16. Для каждого значения c₁ и c₂ вычисляют векторы независимых выходов

и

17. Для каждой пары векторов и рассчитывают и запоминают двумерный сигнал удельной активности , j=1, 2.

18. Для каждого двумерного сигнала производят операции пп.6-13 до выполнения условия п.14.

19. Из оценок сигналов найденных при решении задачи идентификации ядерного взрыва, при соответствующем двумерном сигнале выбирают ту, при которой значение минимально.

20. В качестве момента сепарации принимают t_q, при котором отношение минимально.

На общей блок-схеме алгоритма (Фиг.2) блок «Ввод интервала сепарац