Вычисление параметров преобразования для обработки изображений

Вычисление параметров преобразования для обработки изображений

Иллюстрации

Показать все

Реферат

Изобретение относится, в целом, к способу получения параметров преобразования.

Изобретение также относится к компьютерной программе и компьютерному программному продукту для получения параметров преобразования. Кроме того, изобретение относится к устройству для получения параметров преобразования и использованию способа получения параметров векторного преобразования движения в системах сжатия видеоданных.

Оценка движения играет важную роль во многих областях обработки изображений. Например, при сжатии видеоданных необходимо прогнозировать значения пикселей в последовательных видеокадрах. Прогнозирование позволяет вычислять значения пикселей на приемнике без их передачи по каналу связи. Целью прогнозирования является минимизация общего различия с фактическими значениями пикселей, чтобы приемник мог вычислять наилучшее возможное изображение. При минимальном общем различии в прогнозируемых значениях пикселей значительно меньший объем данных приходится кодировать и передавать для реконструкции исходного кадра.

Данные изображения содержат прогнозируемые значения в виде векторных полей и ошибки или остатка. Величина остатка зависит от точности векторного поля. Векторное поле является описанием модели движения для значений пикселей.

Получение векторного поля описано в de Haan, Biezen, "Sub-pixel motion estimation with 3-D recursive search block-matching", Signal Processing: Image Communications 6, 1994, стр. 229-239.

Однако получение параметров преобразования из векторных полей требует больших объемов вычислений.

Поэтому, одна задача изобретения состоит в обеспечении получения параметров преобразования при небольшом объеме вычислений. Другая задача изобретения состоит в обеспечении оптимальной модели движения для прогнозирования движения. Еще одна задача изобретения состоит в обеспечении повышенного сжатия изображений.

Для решения этих и других задач изобретения предусмотрен способ получения параметров преобразования из векторного поля, содержащий этапы, на которых проецируют векторное поле на, по меньшей мере, одну ось, и выводят параметры преобразования из проекции векторного поля.

Например, векторное поле, описывающее оцененные векторы движения в изображении, в частности, в видеоизображении, можно получить с использованием общего метода прогнозирования движения. Параметры преобразования, например, переноса, масштабирования и поворота, можно получить проецированием векторного поля на, по меньшей мере, одну ось. Векторное поле может содержать векторы. Векторы могут содержать, по меньшей мере, две составляющие, например, x-составляющую и y-составляющую. x-составляющая может быть перпендикулярна y-составляющей. Векторное поле можно описать в системе координат с соответствующими осями. Одна ось может быть осью x, а другая ось может быть осью y. Возможны и другие системы координат. Параметры преобразования могут описывать параметры модели движения. Параметры преобразования можно использовать для генерации векторных полей. Параметры преобразования можно легко получать, когда векторное поле проецируется на, по меньшей мере, одну из осей, предпочтительно, на обе оси. В частности, при проецировании векторов в векторных полях на каждую из осей системы координат и использовании всех выведенных функций можно легко получить параметры преобразования.

Векторы могут содержать, по меньшей мере, две составляющие, по одной на каждую ось. Каждая из составляющих может быть параллельна одной из осей системы координат. В этом случае проецирование на оси позволяет получать соответствующие составляющие векторов в векторном поле.

Проецируя векторное поле на, по меньшей мере, одну ось, можно изолировать параметры преобразования. Например, параметр масштабирования, параметр переноса и параметр поворота можно изолировать с использованием проекции. Из этих проекций можно получить значения множителей и средние значения, которые можно использовать для вычисления коэффициента усиления, например, параметра масштабирования или параметра поворота и/или параметра смещения, например переноса соответственно.

Например, в приложениях можно легче манипулировать параметрами модели движения, например, когда нужно стабилизировать самодельную видеосерию. Для этого может потребоваться знание параметров переноса и поворота. Вычислив эти параметры, изображение как целое можно переносить и поворачивать. Это может дать лучшие результаты, чем манипулирование отдельными векторами.

Кроме того, векторное поле движения как таковое может не всегда быть точным и, поэтому, отыскание параметров модели движения согласно вариантам осуществления может усреднять ошибки, например, отклонения и/или выбросы. Когда векторное поле движения точно, объекты в последовательности могут двигаться иначе, чем камера, что дает сложное векторное поле движения. Если движение объектов достаточно мало, то, по вышеуказанной причине, движение этих объектов может усредняться. В общем случае параметры модели движения согласно вариантам осуществления могут представлять глобальное движение.

Из проекций можно получить параметры полного преобразования. Например, согласно вариантам осуществления, уравнение перемещения можно вычислить, спроецировав все векторы на все оси. Матрицы уравнения преобразований имеют неизвестные элементы, однако эти элементы можно получить из тригонометрического уравнения. Например, множители и средние значения проекций векторных полей можно получить методом аппроксимации кривой. Например, вычисляя аппроксимирующую кривую методом наименьших квадратов расстояний до этой кривой или методом полиномиальной аппроксимации, или методом экспоненциальной аппроксимации. Таким образом, можно вычислить коэффициент усиления и смещение, т.е. масштабирование/поворот и перенос. Такой вариант осуществления представляет собой пример оптимизации в отношении сложности, т.е. простоты реализации и быстроты выполнения. Такой вариант осуществления позволяет получать смещение и коэффициент усиления.

Согласно другим вариантам осуществления эти значения можно получить с использованием примитивной функции проекций. Примитивные функции согласно вариантам осуществления можно получить с использованием метода Эйлера.

С помощью примитивных функций можно вычислить площадь проекции, которая связана с множителем. Устранив среднее значение или параметр переноса, получаем, что полная площадь проекции связана с экстремумом примитивной функции. Экстремум примитивной функции может находиться в точке, где ее производная равна нулю. Найдя экстремум примитивной функции, можно вычислить значение множителя.

Поскольку движение часто моделируется переносом, масштабированием и поворотом, и это движение чаще всего обусловлено движением камеры, параметры переноса представляют согласно вариантам осуществления глобальную модель движения камеры.

Согласно вариантам осуществления можно также применять рекурсивный метод. Векторное поле на основании параметров векторного преобразования можно реконструировать и передать обратно в качестве начальной оценки движения для вычисления векторного поля.

Другой вариант осуществления может предусматривать вычисление параметров преобразования с использованием рекурсивного вычисления. Параметры преобразования можно получить с использованием вышеописанных вариантов осуществления. Затем эти параметры можно использовать для реконструкции векторного поля. В этом реконструированном векторном поле можно идентифицировать выбросы, присутствующие в исходном векторном поле. Эти выбросы можно маскировать. Замаскировав выбросы в векторном поле, можно вычислить новые параметры векторного преобразования, получив лучшие результаты.

Согласно еще одному аспекту изобретения предусмотрена компьютерная программа, способная предписывать процессору, в ходе его работы, получать параметры преобразования посредством получения векторного поля векторов движения, описывающего оцененные векторы движения в изображении, проецирования векторного поля на, по меньшей мере, одну ось и вывода параметров преобразования из проекции векторного поля.

Согласно еще одному аспекту изобретения предусмотрен компьютерный программный продукт, содержащий компьютерную программу, выполненную с возможностью предписывать процессору, в ходе его работы, получать параметры преобразования посредством получения векторного поля, проецирования векторного поля на, по меньшей мере, одну ось и вывода параметров преобразования из проекции векторного поля.

Согласно еще одному аспекту изобретения предусмотрено устройство, предназначенное для получения параметров преобразования, содержащее средство оценки, предназначенное для получения векторного поля, средство проецирования, предназначенное для проецирования векторного поля на, по меньшей мере, одну ось и средство вычисления, предназначенное для вывода параметров преобразования из проекции векторного поля.

Согласно еще одному аспекту изобретения предусмотрено использование способа по п.1 при сжатии видеоданных.

Эти и другие аспекты изобретения описаны и проиллюстрированы со ссылкой на следующие фигуры.

Фиг.1 - логическая блок-схема способа согласно вариантам осуществления изобретения.

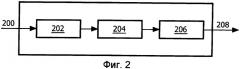
Фиг.2 - устройство для обеспечения способа согласно вариантам осуществления изобретения.

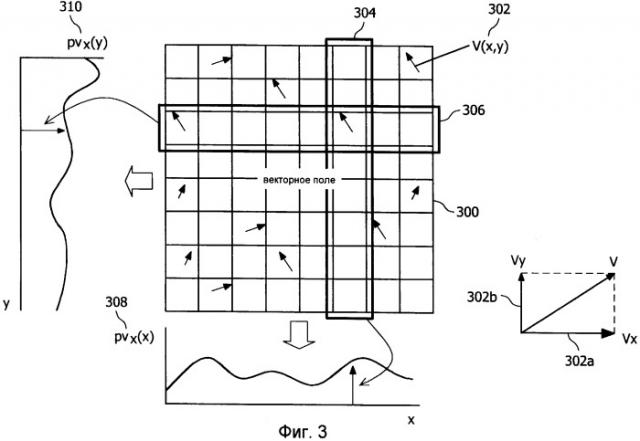
Фиг.3 - проекция x-составляющих векторов на ось x и ось y.

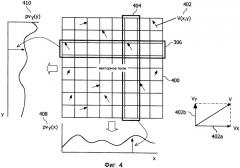
Фиг.4 - проекция y-составляющих векторов на ось x и ось y.

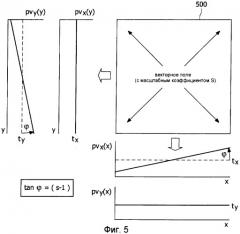
Фиг.5 - преобразование масштабирования векторного поля.

Фиг.6 - преобразование поворота векторного поля.

Фиг.7 - соотношение между коэффициентом усиления и функцией проекции.

На фиг.1 показана логическая блок-схема способа получения параметров преобразования из видеоизображений.

Пиксельное движение, в основном, обусловлено движениями камеры. Поэтому, один подход к улучшению оценки движения состоит в обеспечении глобальной модели движения камеры. Это движение можно моделировать посредством значений переноса, масштабирования и поворота. Перенос, масштабирование и поворот можно описать математическими моделями, которые будут объяснены ниже. Далее мы будем пользоваться следующими переменными:

v_q (bx, by): q-составляющая вектора в позиции (bx, by),

pv_q(r): проекция q-составляющей векторов как функция r,

bq: индекс вектора в векторном поле,

N_bq: количество векторов в направлении q,

q и r: x или y,

x: составляющая векторного поля по оси x,

y: составляющая векторного поля по оси y,

x': преобразованная x-составляющая векторного поля после оценки движения,

y': преобразованная y-составляющая векторного поля после оценки движения,

Θ: угол поворота,

s: параметр масштабирования,

t: параметр переноса.

Предполагая, что начало координат находится в центре кадра изображения, перенос можно описать в виде

Преобразование масштабирования можно описать в виде

В частности, в области обработки видеосигнала, параметр масштабирования часто может определяться оптическими свойствами камер и тем, что аспектное отношение пикселя равно 1. В этом случае параметр масштабирования s может быть единственным параметром. Тогда вышеприведенное уравнение сводится к

Поворот камеры можно описать в виде

Общее преобразование можно описать в виде поворота, масштабирования и переноса согласно следующему уравнению.

Для вычисления параметров преобразования необходимо векторное поле оцененных векторов движения. Поэтому, это векторное поле вычисляется (100) общеизвестными методами. С помощью этого векторного поля осуществляется проецирование x-составляющей векторного поля на ось x (102). Это проецирование можно описать в виде

x-составляющую векторного поля можно также спроецировать на ось y (104), и проекцию можно описать в виде

Проекция x-составляющих на оси показана на фиг.3. Изображено векторное поле 300 с оцененными векторами движения V(x,y) 302. Каждый вектор V(x,y) 302 можно разделить на x-составляющие 302a и y-составляющие 302b. Изображение можно сегментировать на столбцы 304 и строки 306.

Каждый столбец 304 можно проецировать на ось x. Среднее x-составляющих векторов всех векторов в каждом из столбцов 304 рассматривается как проекция pv_x(столбец). Проекция по всем столбцам дает функцию проекции pv_x(x) 308.

Каждую строку 306 можно проецировать на ось y. Среднее x-составляющих векторов всех векторов в каждой из строк 306 рассматривается как проекция pv_x(строка). Проекция по всем строкам дает функцию проекции pv_x(y) 310.

Результирующие функции проекции pv_x(x) 308 и pv_x(y) 310 представляют средние значения x-составляющих векторов в поле 300 оцененных векторов движения.

Помимо x-составляющих векторного поля, также можно проецировать y-составляющие векторного поля. Проекцию на ось x (106) можно описать в виде

и проекцию на ось y (108) можно описать в виде

Проекция y-составляющих на оси показана на фиг.4. Одинаковые элементы обозначены соответствующими позициями, например, 400 относится к 300 и т.д.

Показано векторное поле 400 с оцененными векторами движения V(x,y) 402. Каждый вектор V(x,y) 402 можно разделить на x-составляющие 402a и y-составляющие 402b. Изображение можно сегментировать на столбцы 404 и строки 406.

Каждый столбец 404 можно проецировать на ось x. Среднее y-составляющих векторов всех векторов в каждом из столбцов 404 рассматривается как проекция pv_y(столбец). Проекция по всем столбцам дает функцию проекции pv_y(x) 408.

Каждую строку 406 можно проецировать на ось y. Среднее y-составляющих векторов всех векторов в каждой из строк 306 рассматривается как проекция pv_y(строка). Проекция по всем строкам дает функцию проекции pv_y(y) 410.

Результирующие функции проекции pv_x(x) 308 и pv_x(y) 310 представляют средние значения x-составляющих векторов в поле 300 оцененных векторов движения.

Применяя преобразование масштабирования и перенос к векторному полю, его можно переписать в виде

Проекцию на ось x x-составляющей, подвергнутой масштабированию и переносу, можно описать в виде

которая является функцией первого порядка относительно x, где параметр масштабирования s является множителем, и перенос t_x равен среднему значению.

Кроме того, проекцию x-составляющей векторного поля на ось y можно выразить как

где перенос t_x является постоянной величиной. Кроме того, проекцию y-составляющей векторного поля на ось x можно выразить как

где перенос t_y является постоянной величиной. Наконец, проекцию y-составляющей векторного поля на ось y можно выразить как

которая является функцией первого порядка относительно y, где параметр масштабирования s является множителем, и перенос t_y равен среднему значению. Вышеприведенные уравнения показывают, что параметры переноса и масштабирования можно вывести из свойств проекций векторного поля на оси. Коэффициент усиления/множитель (tanφ) связан с параметром масштабирования или параметром поворота, а среднее значение функции проекции может представлять перенос.

Помимо преобразования переноса и масштабирования, можно также описать поворот камеры. Смещение векторного поля, обусловленное поворотом, можно описать в виде

R обозначает матрицу поворота, I - единичную матрицу и T - перенос.

Проекцию x-составляющей векторного поля на ось x можно описать в виде

Проекцию x-составляющей векторного поля на ось y можно описать в виде

Проекцию y-составляющей векторного поля на ось x можно описать в виде

и проекцию y-составляющей векторного поля на ось y можно описать в виде

Из вышеприведенного описания следует, что поворот можно определить посредством свойств проекции векторного поля. Каждая из проекций содержит множитель и угол поворота в качестве параметра преобразования.

Общее преобразование можно описать в виде следующего уравнения перемещения

Элементы матрицы преобразования s и θ можно задать в виде

каковые параметры можно определить из тригонометрических уравнений

Вычислив проекции составляющих вектора на ось, можно вычислить (110) множитель и средние значения проекций для получения параметров преобразования.

На фиг.5 показана связь преобразования масштабирования с функциями проекции. Показано векторное поле 500, причем изображение подвергнуто преобразованию масштабирования посредством изменения масштаба изображения. Как можно видеть из функции проекции pv_x(x) x-составляющих на ось x и функции проекции pv_y(y) y-составляющих на ось y, коэффициент масштабирования s непосредственно связан с углом φ функции проекции. Связь выражается как tanφ = (s-1). Масштабирование не влияет на функцию проекции pv_y(x) y-составляющих на ось x и функцию проекции pv_x(y) x-составляющих на ось y.

На фиг.6 показана связь преобразования поворота с функциями проекции. Показано векторное поле 600, причем изображение подвергнуто преобразованию поворота на угол θ. Можно видеть, что поворот непосредственно связан с углом φ₁ функции проекции pv_x(x) x-составляющей на ось x и с углом φ₂ функции проекции pv_y(x) y-составляющей на ось x. Кроме того, поворот непосредственно связан с углом φ₂ функции проекции pv_x(y) x-составляющей на ось y и с углом φ₁ функции проекции pv_y(y) y-составляющей на ось y. Связь выражается как tanφ₁ = cosθ - 1 и tanφ₂ = sinθ.

Эти коэффициент усиления и множитель значения можно получить с использованием примитивной функции проекций. С помощью примитивной функции можно определить площадь проекции, которая связана с множителем. Устраняя среднее значение или параметр переноса, получаем, что полная площадь проекции связана с экстремумом примитивной функции.

Вычтя средние значения из функций проекции, можно получить точки экстремума примитивных функций, которые позволяют вычислить коэффициент усиления и множитель. Например, на фиг.7 показана связь между функцией проекции и коэффициентом усиления/множителем. Функция проекции pv_x(x) x-составляющих на ось x обозначена 700. Сначала можно устранить среднее значение t_x, поскольку это значение может представлять перенос. Результирующая функция 702 может представлять только коэффициент усиления.

Площадь функции 702 можно связать с коэффициентом усиления. Интегрируя функцию 702 с использованием метода Эйлера с рекурсивным слагаемым, можно получить примитивную функцию 704. Максимум функции 704 можно связать с коэффициентом усиления.

Подставляя его в члены, например, при рассмотрении только x-составляющей векторного поля в проекции на ось x, получаем

где bs_x - соответствующий размер блока векторов. Экстремум примитивной функции находится в точке, где ее производная равна нулю. В этом случае - это нуль. В точке нуль примитивная функция равна

и это значит, что, найдя экстремум примитивной функции, множитель можно вычислить посредством вышеприведенного уравнения. Проекции на другие оси можно использовать для получения всех остальных значений.

На фиг.2 показано устройство для осуществления вычисления параметров переноса. Входной видеосигнал поступает на клемму 200. В схеме 202 оценки движения оцениваются векторы движения. Оценку векторов движения можно осуществлять на последовательных кадрах входного видеосигнала. Например, использование трех последовательных изображений позволяет определять вектор движения пикселей в трех последовательных кадрах. С помощью оцененных векторов движения схема 202 оценки движения выдает векторное поле, описывающее движение пикселей. Этот выходной сигнал поступает на схему 204 проецирования. Схема 204 проецирования проецирует составляющие векторов движения на оси системы координат. Схема 204 проецирования выводит значения соответствующих проекций векторов движения на соответствующую ось. Эта проекция используется в вычислительной схеме 206 для получения параметров переноса. В вычислительной схеме 206 вычисляются множители и средние значения проекций векторного поля. Это можно делать с использованием метода полиномиальной аппроксимации или примитивной функции проекции. Это можно делать с использованием метода Эйлера. Вычислительная схема 206 выводит параметры преобразования для описания модели движения для движения камеры.

Точность модели преобразования зависит от точности векторного поля. Она также зависит от согласованности векторного поля. Точность модели преобразования снижается, когда объекты в кадре движутся помимо движения камеры.

Параметры выводятся на выходную клемму 208.

1. Способ получения параметров преобразования для основывающейся на прогнозировании обработки изображений, содержащий этапы, на которых получают векторное поле, описывающее оцененные векторы движения для пикселей изображения; проецируют векторное поле на по меньшей мере одну ось, причем при данном проецировании для каждой из упомянутой по меньшей мере одной оси получают функцию проекции посредством усреднения составляющих векторов движения, соответствующих этой оси; и выводят параметры преобразования, описывающие модель движения, из проекции векторного поля с использованием функций проекции.

2. Способ по п.1, в котором векторное поле содержит векторы, имеющие по меньшей мере одну первую составляющую и по меньшей мере одну вторую составляющую, при этом первая составляющая параллельна первой оси, а вторая составляющая параллельна второй оси.

3. Способ по п.2, в котором при проецировании по меньшей мере одной составляющей на по меньшей мере одну ось изолируют по меньшей мере параметр масштабирования.

4. Способ по п.3, в котором параметр масштабирования вычисляют из по меньшей мере одного множителя проекции(й) на по меньшей мере одну ось.

5. Способ по п.2, в котором при проецировании по меньшей мере одной составляющей на по меньшей мере одну ось изолируют по меньшей мере параметр переноса.

6. Способ по п.5, в котором параметр переноса вычисляют из среднего значения проекции на одну ось.

7. Способ по п.2, в котором при проецировании по меньшей мере одной составляющей на по меньшей мере одну ось изолируют по меньшей мере параметр поворота.

8. Способ по п.7, в котором параметр поворота вычисляют из по меньшей мере одного множителя проекции(й) на по меньшей мере одну ось.

9. Способ по п.1, в котором параметры преобразования получают путем применения алгоритма аппроксимации кривой к проекциям.

10. Способ по п.1, в котором параметры преобразования получают из примитивных функций проекции.

11. Способ по п.10, в котором примитивная функция является эйлеровой функцией.

12. Способ по п.10, в котором по меньшей мере один параметр вычисляют из экстремума примитивной функции.

13. Способ по п.1, в котором параметры преобразования представляют глобальную модель движения камеры.

14. Устройство для оценки движения при обработке изображений, содержащее средство оценки для получения векторного поля, описывающего оцененные векторы движения для пикселей изображения; средство проецирования для проецирования векторного поля на по меньшей мере одну ось путем получения для каждой из упомянутой по меньшей мере одной оси функции проекции посредством усреднения составляющих векторов движения, соответствующих этой оси; и средство вычисления для вывода параметров преобразования, описывающих модель движения, из проекции векторного поля с использованием функций проекции.