Устойчивая к коллективным атакам десинхронизация для цифрового помечания видео

Устойчивая к коллективным атакам десинхронизация для цифрового помечания видео

Иллюстрации

Показать все

Реферат

Быстрое распространение цифрового мультимедиа наряду с постоянно увеличивающейся пропускной способностью интернет-связи делает управление цифровым авторским правом все более и более сложной задачей. Поскольку любой конечный пользователь, принимающий копию информационного содержимого (контента) мультимедиа, может распространить эту копию другим пользователям, должен быть установлен механизм для отслеживания незаконного распространителя, чтобы защитить цифровое авторское право. Помечание (fingerprinting) мультимедиа является способом встраивания уникальных идентификаторов в контент мультимедиа каждого пользователя. Поскольку примененная метка уникально привязана к пользователю, которому была выдана копия, извлечение этой метки в пиратской копии однозначно определяет пользователя, привязанного к метке.

Поскольку данные мультимедиа можно немного изменить, не вызывая искажения восприятия, метка может быть введена в пределах данных без ухудшения восприятия конечным пользователем. Имеется множество предшествующих работ по введению меток в изображение и звуковой сигнал. Однако исследования по введению меток в видео были весьма ограничены. Обычно, если изменяется сигнал-носитель для помечания, также должна быть адаптирована схема помечания. Например, в цветном изображении сцен природы пространство для помечания обычно намного больше, чем в двухуровневом (черно-белом) изображении. Естественно, мы можем ожидать от видео больших возможностей для встраивания. Однако большой объем данных в видео привносит как благоприятные, так и неблагоприятные аспекты. Благоприятный аспект состоит в том, что возможность для встраивания у видео намного выше, чем у неподвижных изображений, и поэтому надежность помечания увеличивается. Неблагоприятный аспект состоит в том, что пространственная и временная избыточность видеосигналов может быть использована злоумышленниками. Поэтому проектирование и разработка схем помечания видео являются более сложными, чем помечания неподвижных изображений и аудио.

Несмотря на усилие проектировщиков меток защитить цифровое авторское право, злоумышленники также имеют сильный стимул удалить метку. Например, популярные системы маркетинга отправляют популярные кинофильмы в кинотеатры перед тем периодом времени, в течение которого они продаются "на видео", например, на DVD-носителе. Если пират может продать кинофильм на DVD во время его проката в кинотеатрах, может быть получена огромная прибыль. При атаке на схему помечания цель злоумышленников состоит в том, чтобы ввести в заблуждение датчик меток, с тем, чтобы он не смог обнаружить или правильно идентифицировать метку. Для злоумышленников временная сложность и качество восприятия также являются важными соображениями, поскольку ценность мультимедиа частично состоит в его своевременности и качестве восприятия. Соответственно, группа злоумышленников, каждый из которых владеет помеченной копией видео, может сговориться сформировать коллективную атаку. Такая атака пытается ослабить или удалить метку, введенную в каждую копию. Когда количество помеченных копий в коллективной атаке является достаточно большим, например 30-40, полезность метки снижается настолько, что для датчика меток может стать невозможным обнаружить наличие метки в копии, подвергшейся коллективной атаке.

СУЩНОСТЬ ИЗОБРЕТЕНИЯ

Описана десинхронизация, стойкая к коллективным атакам злоумышленников, для использования при помечании цифрового видео, в которой видео, которое должно быть защищено, десинхронизируют и тем самым создают одну или более помеченных копий видео. В одной реализации видео, которое должно быть защищено, десинхронизируется во времени и десинхронизируется в пространстве. Создается помеченная копия видео, измененная посредством временной и пространственной десинхронизации.

ПЕРЕЧЕНЬ ЧЕРТЕЖЕЙ

Подробное описание дано со ссылкой на сопроводительные чертежи. На чертежах крайняя левая цифра (цифры) номера для ссылок идентифицирует фигуру, в которой номер для ссылок впервые появляется. Использование одних и тех же номеров для ссылок на разных фигурах указывает сходные или идентичные элементы.

Фиг.1 показывает иллюстративную шкалу времени, позволяющую сравнивать однородно дискретизированные индексы времени и случайным образом дискретизированные индексы времени.

Фиг.2 показывает иллюстративные аспекты временной десинхронизации, включающие в себя стратегии аффинной деформации, при которой кадр F₁ деформируется в кадр F₂.

Фиг.3 показывает иллюстративные аспекты временной десинхронизации, включающие в себя стратегии аффинной деформации, при которой деформируются оба кадра F₁ и F₂.

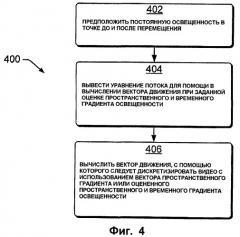
Фиг.4 показывает иллюстративные аспекты временной десинхронизации, включающие в себя стратегии оптического потока.

Фиг.5 показывает иллюстративные аспекты временной десинхронизации, включающие в себя стратегии переключения векторов движения.

Фиг.6 показывает иллюстративные аспекты временной десинхронизации, включающие в себя стратегии временной интерполяции с компенсацией движения.

Фиг.7 показывает иллюстративные аспекты псевдослучайных индексов времени для повторной временной дискретизации.

Фиг.8 показывает иллюстративные аспекты временной десинхронизации, включающие в себя стратегии случайной повторной временной дискретизации.

Фиг.9 показывает иллюстративные аспекты временной десинхронизации, включающие в себя стратегии с пропуском интерполяции.

Фиг.10 показывает иллюстративные аспекты пространственной десинхронизации, включающие в себя стратегии поворота, масштабирования и сдвига (RST).

Фиг.11 показывает иллюстративные аспекты пространственной десинхронизации.

Фиг.12 показывает иллюстративные аспекты пространственной десинхронизации, включающие в себя стратегии изгиба.

Фиг.13 показывает иллюстративные аспекты пространственной десинхронизации, включающие в себя стратегии фильтрации яркости.

Фиг.14 показывает иллюстративные аспекты пространственной десинхронизации, включающие в себя стратегии дискретизации параметров.

Фиг.15 показывает иллюстративные аспекты пространственной десинхронизации, включающие в себя стратегии сглаживания во времени.

Фиг.16 показывает иллюстративные аспекты пространственной десинхронизации, включающие в себя стратегии распределения параметров.

Фиг.17 показывает иллюстративную вычислительную среду, подходящую для реализации устойчивой к коллективным атакам десинхронизации для помечания цифрового видео.

ПОДРОБНОЕ ОПИСАНИЕ

Последующее описание направлено на системы и способы, которые борются с коллективными атаками, при которых два или более получателей помеченных копий контента мультимедиа (например, цифрового универсального диска DVD с аудио- и видеоконтентом, таким как кинофильм) пытаются скомбинировать свои копии, чтобы создать высококачественную версию без меток. В частности, разработаны системы и способы, приводящие к формированию артефактов восприятия, если помеченные копии повторно комбинируются.

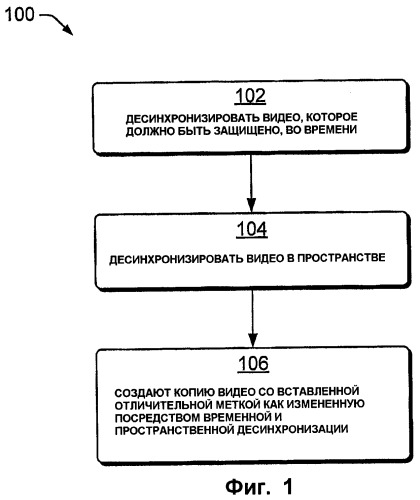
Фиг.1 показывает иллюстративную методику 100 десинхронизации, используемую для помечания контента мультимедиа, чтобы противостоять коллективным атакам. В варианте воплощения, показанном на фиг.1, устойчивая к коллективным атакам схема десинхронизации включает в себя видеодесинхронизацию как во временной, так и в пространственной области. Каждая пользовательская копия видео немного изменена таким образом, что изменения не будут заметны для каждой индивидуальной копии, но будут достаточно существенны, чтобы произвести артефакты восприятия, когда несколько копий комбинируются (например, такими способами, как усреднение). Так как физические характеристики временной оси и пространственной оси значительно отличаются, временная и пространственная десинхронизация обычно разделяются на два этапа. На первом этапе сначала применяется ограниченная псевдослучайная дискретизация во временной области. Принимая во внимание, что набор видеокадров однородно дискретизирован по оси времени, используется интерполяция кадров на основе движения для формирования новых видеокадров в произвольных индексах времени. На втором этапе каждый видеокадр дополнительно десинхронизируется посредством глобальной геометрической операции, включающей в себя поворот, масштабирование и сдвиг, за которыми следует локальный случайный изгиб с использованием случайно выбранной сетки пространственной дискретизации. Проблемы качества восприятия решаются посредством сглаживания параметров десинхронизации по пространственной и временной осям. Кроме того, проблема безопасности десинхронизации анализируется в контексте вычислительной сложности.

В частности, фиг.1 показывает пример 100 варианта воплощения, в котором псевдослучайная временная дискретизация видео и методики пространственной десинхронизации объединены для получения помеченных копий видео, для которых может быть отслежен первоначальный получатель, и которые приводят к дефектной копии, поврежденной посредством видимых артефактов, при комбинировании со сходными помеченными копиями. На этапе 102 видео, которое должно быть защищено, подвергается временной десинхронизации. На этапе 104 видео подвергается пространственной десинхронизации. На этапе 106 создается помеченная копия видео, измененного посредством временной и пространственной десинхронизации.

Псевдослучайная временная дискретизация видео

Эта глава подробно останавливается на временной десинхронизации, теме, внесенной на рассмотрение этапом 102 на фиг.1. Временная десинхронизация может использовать псевдослучайную временную дискретизацию, включающую в себя интерполяцию видеокадров. Основная проблема, связанная с интерполяцией видеокадров, состоит в том, что для заданной пары близких во времени видеокадров (например, кадра F₁ в момент времени t₁ и кадра F₂ в момент времени t₂, причем (t₂>t₁) и T=t₂-t₁ является периодом кадров исходного видео) мы хотим сформировать промежуточный кадр в момент времени (t₁+Δ·Т), где 0≤Δ≤1. Во многих случаях прямое усреднение соответствующих пикселов кадра не будет давать хороший результат, поскольку объекты в видеокадрах имеют тенденцию перемещаться, и такое движение должно быть принято во внимание при проведении интерполяции. В соответствии с этим, имеется потребность в более сложных методиках.

Временная десинхронизация может использовать псевдослучайную временную дискретизацию. Псевдослучайная временная дискретизация видео может использовать стратегию аффинной деформации для обеспечения основы для интерполяции видеокадров. Например, если заданы два видеокадра F₁ и F₂, полезно деформировать кадр F₁ в кадр F₂. Координаты в кадре F₁ можно обозначить как (x₁, y₁) и в кадре F₂ - как (х₂, y₂). Однородные координаты можно использовать для описания двухмерной аффинной деформации кадра F₁ в кадр F₂ в соответствии с уравнением:

Матрица аффинного преобразования обозначена в указанном выше уравнении как W. Параметры w₁-w₆ учитывают операции поворота, масштабирования и сдвига. Все эти параметры сначала оцениваются на изображениях кадров F₁ и F₂ с меньшей дискретизацией, затем масштабируются и уточняются для изображений большего размера, пока окончательно не будет достигнут первоначальный размер кадров.

Поиск параметров включает в себя нахождение решения задачи минимизации. Обозначим операцию деформирования кадра как warp_w(·) и показатель расстояния, который служит мерой расстояния между двумя кадрами, как dist(·,·). Поскольку операция деформирования уникально определена параметрами деформирования, попытаемся найти такой вектор параметров w*=[w₁*w₂*w₃*w₄*w₅*w₆*]^T, что

Когда показатель расстояния является суммой квадратов разностей, указанная выше формула становится задачей метода наименьших квадратов. Такая задача может быть решена с помощью классического алгоритма Лукаса - Канаде (Lucas - Kanade), который по существу использует метод Гаусса - Ньютона для нахождения минимумов.

Чтобы сократить вычислительную сложность из-за высокой размерности, заметим, что параметры сдвига w₃ и w₆ могут быть отделены от других параметров. Поэтому сначала могут быть определены параметры w₃ и w₆, после чего выполняется итерационная процедура для обновления вектора параметров, пока он не будет сходиться.

В соответствии с этим, решение аффинной деформации может быть применено посредством вывода уравнения, описывающего аффинную деформацию кадра F₁ в кадр F₂ в пределах видео, такого как уравнение (1). Получив уравнение, вектор параметров, описывающий деформацию, может быть найден с помощью решения задачи минимизации, полученной из уравнения, такого как уравнение (2).

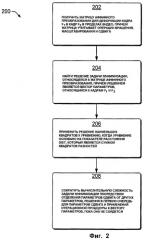
Фиг.2 показывает вариант 200 воплощения временной десинхронизации, характеризуемый решением методом аффинной деформации, в котором кадр F₁ деформируется в кадр F₂. Решение методом аффинной деформации находят в пределах такого набора Ф функций деформации, что для любого заданного изображения I посредством применения функции деформации ϕ_k(·)∈Ф к изображению I может быть сформировано деформированное изображение I′, то есть I′=φ_k(I), для распространения пользователю k. Таким образом, каждый пользователь получит отличающуюся копию изображения I, и тем самым усложняется коллективная атака. На этапе 202 получают матрицу аффинного преобразования для деформации кадра F₁ в кадр F₂ в видео, причем матрица учитывает операции поворота, масштабирования и сдвига (RST). Уравнение (1) является типичным для матрицы аффинного преобразования. На этапе 204 находят решение задачи минимизации, относящейся к матрице. Уравнение (2) является типичным для задачи минимизации. Задача минимизации может решаться любым соответствующим способом. Например, на этапе 206 применяют решение методом наименьших квадратов, в котором уравнение основано на показателе расстояния dist, являющемся суммой квадратов разностей. На этапе 208 может быть сокращена вычислительная сложность задачи минимизации посредством отделения параметров сдвига от других параметров, решения в первую очередь для параметров сдвига и применения итерационной процедуры к вектору параметров до тех пор, пока она не сойдется. Таким образом, в приведенном выше примере сначала были определены параметры w₁ и w₆, и тем самым была сокращена размерность задачи для облегчения нахождения решения для оставшихся параметров.

Приведенное выше рассмотрение фиг.2 относится к интерполяции видеокадра вообще и, в частности, к инструменту аффинной деформации для псевдослучайной временной дискретизации. При этих обстоятельствах мы видели, что для заданных двух видеокадров F₁ и F₂ выгодно деформировать кадр F₁ в кадр F₂. Альтернативный инструмент аффинной деформации, представленный на фиг.3 и адаптированный к аналогичному применению, может успешно деформировать оба кадра F₁ и F₂.

Предположим, что заданы кадр F₁ в момент времени t₁ и кадр F₂ в момент времени t₂ и мы хотим деформировать оба кадра F₁ и F₂ в направлении к моменту времени (t₁+Δ·T), где 0<Δ<1. Сначала мы оцениваем матрицу W деформации кадра F₁ в кадр F₂. Затем матрицы W_F и W_B прямого и обратного аффинных преобразований, которые деформирует кадр F₁ и кадр F₂ по направлению к моменту времени (t₁+Δ·T), могут быть вычислены в соответствии с уравнениями

и

Кадры прямой и обратной деформации, кадр F_fwd из кадра F₁ и кадр F_bwd из кадра F₂, получают посредством повторной дискретизации кадров F₁ и F₂ соответственно в деформированных координатах

Поскольку точка повторной дискретизации может находиться не в целочисленных координатах, для получения выходного значения могут быть использованы такие способы интерполяции, как билинейная интерполяция или кубическая интерполяция.

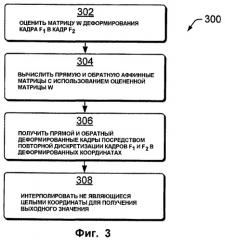
Фиг.3 показывает вариант 300 воплощения временной десинхронизации, характеризуемый вторым решением методом аффинной деформации, в котором оба кадра F₁ и F₂ деформируются в направлении к моменту времени (t1+Δ·Т), где 0≤Δ≤1. Второе решение методом аффинной деформации также находят в пределах такого набора Ф функций деформации, что для любого заданного изображения I посредством применения функции деформации ϕ_k(·)∈Ф к изображению I может быть сформировано деформированное изображение I′, то есть I′=φk(I), для распространения пользователю k. Таким образом, каждый пользователь получит отличающуюся копию изображения I, и тем самым усложняется коллективная атака. На этапе 302 оценивают матрицу W деформации кадра F₁ в кадр F₂. На этапе 304 могут быть вычислены прямая и обратная аффинные матрицы с использованием оцененной матрицы W. Приведенные выше уравнения (3) и (4) являются примерами прямой и обратной матриц. Прямая и обратная матрицы позволяют вычислить прямой и обратный деформированные кадры. В соответствии с этим, на этапе 306, прямой и обратный деформированные кадры получают посредством повторной дискретизации кадров F₁ и F₂ в деформированных координатах. В приведенном выше примере уравнения (5) и (6) показывают, как прямой и обратный кадры F_fwd и F_bwd могут быть получены посредством повторной дискретизации и использования прямой и обратной матриц. На этапе 308, если получены нецелочисленные координаты, может использоваться интерполяция для получения приемлемых выходных значений.

Варианты воплощения псевдослучайной временной дискретизации видео могут использовать стратегию оптического потока для обеспечения основы для интерполяции видеокадров. В соответствии с этим оптический поток может обеспечить псевдослучайную временную дискретизацию видео, которая используется для помечания видео, полученного из видео, которое должно быть защищено. Оптический поток относится к наблюдаемому двухмерному движению в видеоданных. Поскольку человеческий глаз воспринимает движение посредством наблюдения соответствующих точек в разных местоположениях в разное время, идентификация движения основана на предположении постоянной интенсивности, что значение яркости одной и той же точки объекта не изменяется после перемещения. Предположим, что в видео последовательности изменение яркости обозначено f(х, y, t). Предположим, что точка Р объекта в пространственном местоположении (х, y) в момент времени t перемещается в положение (x+dx, y+dy) в момент времени t+dt. При предположении постоянной интенсивности мы имеем уравнение

Предполагая непрерывность поля яркости вдоль пространственной и временной осей, мы можем применить разложение Тейлора к левой стороне уравнения (7), таким образом, уравнение теперь становится уравнением

Тогда мы приходим к уравнению оптического потока

или

где ∇f - вектор пространственного градиента функции f(x, y, t).

Уравнение оптического потока предлагает нам подход к вычислению вектора движения, если мы можем оценить пространственный и временной градиент яркости. В варианте воплощения пространственные градиенты для местоположения (х, y) оцениваются в пределах окна размером 5×5 с центром в (х, y). В соответствии с этим, функция уравнения (10) может быть расширена для вычисления компонентов х и у вектора движения.

Фиг.4 показывает вариант 400 воплощения временной десинхронизации, характеризуемый применением решения оптического решения для повторной дискретизации. В частности, вектор пространственного градиента используется для изменения кадров в видео, тем самым видео деформируется по-разному для каждого пользователя, которому будут распределены копии видео. На этапе 402 предполагают постоянную освещенность f точки (х, y) до и после перемещения. Такое предположение совместимо с естественным прослеживанием, выполняемым человеческим глазом, при котором движение наиболее хорошо наблюдается, когда объект имеет в общем постоянный внешний вид. На этапе 404 выводят уравнение потока. Например, уравнения (9) и (10) являются типичными для уравнений оптического потока, которые помогают в вычислении вектора движения, при заданной оценке пространственного и временного градиента яркости. На этапе 406 вычисляют вектор движения, с помощью которого следует дискретизировать видео с использованием ∇f и оцененного пространственного и временного градиента яркости.

Варианты воплощения псевдослучайной временной дискретизации видео могут использовать стратегию переключения вектора движения для обеспечения основы для интерполяции видеокадров. Переключение вектора движения помогает в выборе вектора движения для коррекции деформации, подразумеваемой матрицей W. Предположим, что заданы кадр F₁ в момент времени t₁ и кадр F₂ в момент времени t₂ (t₂>t₁), и мы хотим сформировать новый кадр в момент времени (t₁+Δ·Т). Сначала мы формируем три пары деформированных кадров. Первой парой являются просто исходные кадры (F₁, F₂). Второй парой являются исходные кадры, подвергнутые аффинной деформации в направлении к моменту времени (t₁+Δ·Т), (F_fwd/F_bwd). Третьей парой являются кадры, подвергнутые аффинной деформации плюс компенсации коррекции движения, (F′_fwd, F′_bwd). где поле движения унаследовано от предыдущего уровня с меньшей дискретизацией. Для каждой пары кадров применяется дифференциальная оценка движения с использованием подхода с оптическим потоком. Это приводит к трем полям векторов движения. Допустим, что это - поля векторов движения v₁(x, y), v₂(x, y) и v₃(x, y). Переключение векторов движения - это процесс определения предпочтительного вектора движения из трех кандидатов векторов движения в местоположении (х, y), который является коррекцией к аффинному деформированию, подразумеваемому матрицей W. Критерий выбора основан на следующей функции ошибки E_v(x, y), которая может рассматриваться как практическая форма уравнения (10) оптического потока

где

, ,

и S - малое окно с размерами 5×5 пикселей и с центром в точке (х, y). Вектор движения v(x, y) является постоянным по суммированию, и ∇f_x, ∇f_y и ∇f_t являются функциями от (х, y). Такая формулировка может быть решена посредством классического алгоритма Лукаса - Канаде, который является по существу способом Гаусса - Ньютона итерационного решения данной задачи численной оптимизации. Используя упомянутую выше функцию ошибки, являющийся кандидатом вектор движения, который достигает минимальной ошибки в местоположении (х, y), выбирают в качестве нового вектора движения. Для применения в интерполяции мы придаем гладкость вектору движения посредством применения гладкой фильтрации к полю векторов движения с использованием медианного или усредняющего фильтра. Это приводит к конечному полю v векторов движения.

Фиг.5 показывает вариант 500 воплощения временной десинхронизации, характеризуемый применением решения методом переключения векторов движения для повторной дискретизации. На этапе 502 формируют множество пар деформированных кадров. На этапе 504 вектор движения привязывают к каждой паре кадров, тем самым получают множество векторов движения. На этапе 506 функцию ошибки применяют к каждому из векторов движения. Функция ошибки может быть в виде уравнения (11). На этапе 508 функцию ошибки используют для выбора вектора движения для использования во временной десинхронизации.

Варианты воплощения псевдослучайной временной дискретизации видео могут использовать стратегию временной интерполяции с компенсацией движения для обеспечения основы для интерполяции видеокадров. В стратегии временной интерполяции с компенсацией движения исходные кадры могут быть деформированы в направлении к моменту времени. Например, на основе поля v движения исходные кадры F₁ и F₂ деформируются по направлению к моменту времени (t₁+Δ·T), чтобы сформировать два деформированных кадра G₁ и G₂. С этой целью векторы движения являются линейно масштабированными, и деформированный кадр является повторно дискретизированной версией исходного кадра. Например,

и кадр G₂ может быть получен аналогичным образом. Как только мы получаем кадры G₁ и G₂, конечный кадр интерполяции F(x, y) получают как

В соответствии с этим, видео может быть подвергнуто временной десинхронизации посредством применения решения методом временной интерполяции с компенсацией движения к повторной дискретизации. Кадры G₁ и G₂ могут быть сформированы посредством деформирования F₁ и F₂ по направлению к такому моменту времени, как (t₁+Δ·Т). Кадры G₁ и G₂ затем могут быть повторно дискретизированы в соответствии с функцией от F₁ и F₂, такой как уравнение (12). Наконец, интерполированный кадр F может быть получен как функция от G₁ и G₂, например, посредством использования уравнения (13).

Фиг.6 показывает вариант 600 воплощения временной десинхронизации, характеризуемый применением решения методом временной интерполяции с компенсацией движения для повторной дискретизации, в котором исходные кадры F₁ и F₂ и привязанный вектор v движения используются для получения такого интерполированного кадра F, что дискретизация F приводит к дискретизации с помечанием. На этапе 602 формируют кадры G₁ и G₂ посредством деформации кадров F₁ и F₂ по направлению к моменту времени (t₁+Δ·Т). Например, уравнение (12) показывает, как кадр G₁ может быть получен из кадра F₁. На этапе 604 кадры G₁ и G₂ повторно дискретизируют из кадров F₁ и F₂. Например, повторная дискретизация может быть выполнена, в соответствии с уравнением (12). На этапе 606 интерполированный кадр может быть получен как функция от деформированных кадров G₁ и G₂. Например, уравнение (13) представляет собой пример того, как интерполированный кадр F может быть получен из деформированных кадров G₁ и G₂.

Варианты воплощения псевдослучайной временной дискретизации видео могут использовать ограниченную стратегию случайной временной повторной дискретизации для обеспечения основы для интерполяции видеокадра. В одном варианте воплощения формируются псевдослучайные индексы времени по временной оси, дающие возможность повторной дискретизации видео во вновь сформированные моменты времени посредством интерполяции кадра. Чтобы достичь хорошего качества восприятия, мы вносим ограничение, что в повторно дискретизированном видео между двумя интервалами кадра в первоначальном видео, то есть между любым кадром i и i+2 в первоначальном видео, должен находиться, по меньшей мере, один кадр. На фиг.7 можно видеть, что случайно отсчитанный индекс времени расположен между каждым из равномерно отсчитанных индексов времени. Это ограничивает временную пульсацию в повторно дискретизированном видео и в то же время дает место для случайного выбора по времени. Чтобы достичь этой цели, мы сначала формируем независимые, одинаково распределенные случайные приращения времени, Δ_i, которые равномерно распределены в диапазоне [1-δ, 1+δ]. Затем мы инициализируем время t(0)=0 и вычисляем индекс времени t(i)=t(i-1)+Δ_i для i=1, 2, …, N. Здесь N полная длина повторно дискретизированного видео, которая является случайной величиной в соответствии с N ~ Uniform[M(1-α), М(1+α)], где М - общее количество кадров в первоначальном видео. Наконец, мы масштабируем значения от t(1) до t(N), чтобы удостовериться, что все индексы времени попадают в диапазон [0, М].

При такой постановке могут быть выбраны два параметра: δ, который управляет величиной временной пульсации, и α, который управляет изменением длины. В примере, посредством которого может быть реализована временная десинхронизация, δ и α могут быть выбраны как δ=0,75 и α=0,0035. Другие значения могут дать удовлетворительные результаты в различных приложениях этих концепций.

Фиг.8 показывает вариант 800 воплощения временной десинхронизации, характеризуемый применением стратегии случайной временной повторной дискретизации с ограничением для повторной дискретизации, в котором равномерно отсчитанные индексы времени, привязанные к видео, заменяются случайно отсчитанными индексами времени, привязанными к повторной дискретизации. На этапе 802 формируют псевдослучайные индексы времени по временной оси. Затем видео повторно дискретизируют во вновь сформированные моменты времени, например, посредством использования интерполяции кадров. На этапе 804 формирование псевдослучайно отсчитанных индексов времени ограничивают, чтобы, по меньшей мере, один кадр в повторной дискретизации находился между двумя интервалами кадра в первоначальном видео. В примере на фиг.7 можно видеть, что между каждыми двумя первоначальными маркерами кадров (сверху шкалы времени) имеется один псевдослучайный маркер кадра (снизу шкалы времени). На этапе 806 формируют случайные приращения Δ_i времени и равномерно распределяют их в пределах диапазона [1-δ, 1+δ]. На этапе 808 индекс времени инициализируют и вычисляют по длине видео. Например, индекс времени может быть инициализирован в t(0)=0 и вычислен в соответствии с t(i)=t(i-1)+Δ_i для i=1, 2, …, N, где N - длина повторно дискретизированного видео и является случайной величиной в соответствии с N ~ Uniform[M(1-α), М(1+α)]. На этапе 810 значения от t(1) до t(N) масштабируют, чтобы все индексы времени находились в пределах [0, М], где М - общее количество кадров в видео. На этапе 812 могут быть выбраны переменные для управления аспектами видео. В частности, выбирают параметр α для управления длиной изменения и δ для управления временной пульсацией. Например, параметр δ может быть установлен равным 0,75, и параметр α может быть установлен равным 0,0035.

Варианты воплощения псевдослучайной временной дискретизации видео могут использовать стратегию интерполяции с пропусками для улучшения контроля качества. Когда кадры в совокупности образуют быстрое движение и/или сложные сцены, использование интерполяции кадров может не привести к удовлетворительному результату с точки зрения восприятия. Поэтому качеством интерполированного кадра можно управлять посредством пропуска кадров, которые представляют собой быстрое и сложное движение. Количественно дисперсия поля вектора движения может быть вычислена как var(v_x) и var(v_y), причем интерполяция пропускается всякий раз, когда сумма var(v_x)+var(v_y) больше порогового значения V_th. В одной реализации размер кадра может быть установлен равным 640×480 пикселей, и порог V_th может быть установлен равным 300. Вообще, использование меньшего размера кадра должно приводить к пропорциональному уменьшению порога на основе ширины или высоты кадра.

Фиг.9 показывает вариант 900 воплощения стратегии интерполяции с пропусками для улучшения контроля качества. На этапе 902 определяют, какие кадры в видео описывают быстрое движение и сложное видео. Эти кадры представляют потенциальную проблему качества, если применяется псевдослучайная временная дискретизация. На этапе 904 кадры, которые описывают быстрое движение и сложное видео, отмечают и пропускают повторную дискретизацию этих кадров.

Пространственная десинхронизация видео

Эта глава рассматривает пространственную десинхронизацию, тему, внесенную на рассмотрение блоком 104 на фиг.1. Пространственная десинхронизация может использоваться вместе с псевдослучайной временной дискретизацией видео для создания десинхронизации. Одна реализация пространственной десинхронизации включает в себя как глобальные операции, так и локальные операции. Глобальные операции включают в себя поворот, масштабирование и сдвиг (RST) кадра. Локальные операции включают в себя сглаженный переменный случайный изгиб и фильтрацию яркости. Чтобы достичь хорошего качества восприятия, параметры для этих операций формируются сглаженными в пространстве и по времени.

Операции поворота, масштабирования и сдвига (RST) являются одним видом пространственной десинхронизации. Поворот, масштабирование и сдвиг (смещение) могут быть представлены с использованием однородных координат. Пусть координаты перед операциями поворота, масштабирования и сдвига (RST) - это (x1, y1), и после поворота, масштабирования и сдвига (RST) - (x2, y2), поворот на угол θ приведет к следующему соотношению

Аналогично мы можем найти соотношение координат после сдвига на (t_x, t_y)

и соотношение после масштабирования

Полный эффект может быть представлен с использованием комбинации матриц преобразования поворота, сдвига и масштабирования.

В реализации уравнений 14-16 угол θ поворота, коэффициент s_x и s_y масштабирования и величина t_x и t_y сдвига выбираются с таким ограничением, чтобы достичь незаметности операций поворота, масштабирования и сдвига (RST). Соответствующий этому выбор включает в себя: θ∈[-Θ, Θ]; s_x,s_y∈[1-S, 1+S] и t_y∈[-Г, Г]. В этой реализации используется кубическая сплайновая интерполяция, и выбран период Т=32. В одной реализации диапазоны параметров поворота, масштабирования и сдвига (RST) установлены Θ=π/100, S=0,04 и Г равным 1% от размеров кадра.

Фиг.10 показывает вариант 1000 воплощения пространственной десинхронизации, характеризуемый применением стратегии, включающей в себя типично глобальные операции для поворота, масштабирования и сдвига (RST) кадра. На этапе 1002 поворачивают точки в видео, которое должно быть защищено. На этапе 1004 масштабируют точки в видео, которое должно быть защищено. На этапе 1006 сдвигают точки в видео, которое должно быть защищено. Следует отметить, что по желанию могут быть применены одна, две или все из операций поворота, масштабирования и сдвига (RST). Эти операции обеспечивают случайность и составляют часть метки, привносимой в видео.

Случайный изгиб представляет собой инструмент, используемый для пространственной повторной дискретизации изображения в случайных местоположениях подпикселов. Обычно в цифровых изображениях пикселы отсчитываются в однородной сетке, как показано на фиг.11. При случайном изгибе первоначальная сетка дискретизации заменяется псевдослучайной сеткой дискретизации, сформированной с использованием ключа. Количество точек дискретизации до и после изгиба остается неизменным. Чтобы сохранять качество восприятия, должны быть выполнены несколько ограничений. Во-первых, нужно сохранить порядок местоположений дискретизации, то есть, если два местоположения дискретизации, (x_i, y_k) и (x_j, y_k) находятся в одной и той же "строке" и i<j, то x_i<x_j. To же самое правило применяется к упорядочиванию столбцов. Во-вторых, следует удостовериться, что большинство областей приблизительно равномерно дискретизированы. Математически это означает, что для любой выпуклой области S с площадью больше А должна существовать, по меньшей мере, одна точка Р дискретизации внутри области S. Мы выб