Способ распространения информации и предотвращения распространения информации в компьютерной сети

Способ распространения информации и предотвращения распространения информации в компьютерной сети

Иллюстрации

Показать все

Реферат

Область техники, к которой относится изобретение

Настоящее изобретение относится к способам управления сетями (как логическими, так и физическими) в нескольких областях. В частности, настоящее изобретение предлагает способы распространения или предотвращения распространения информации по сети, состоящей из произвольного числа соединенных связями сетевых узлов. Способы, предлагаемые изобретением, основываются на способах анализа сетей, раскрытых в норвежской патентной заявке NO 2003 5852, содержание которой включено в настоящее описание посредством ссылки.

Уровень техники

Общеизвестно, что электронная информация может передаваться значительному числу людей за короткое время. Этот факт является хорошей новостью для некоторых людей (спаммеров, блоггеров), но может быть плохой новостью для ответственных за безопасность. Бесконечна борьба против вирусов, спама и других форм вредоносной или нежелательной, распространяющейся самостоятельно информации.

В изобретении для раскрытия проблемы распространения информации выбран подход с направления сетевого анализа. Настоящее изобретение включает как способы для содействия более эффективному распространению информации, так и способы для затруднения распространения нежелательной информации (например, вирусов). Большая часть исходного обсуждения в раскрытии настоящего изобретения относится к обоим применениям (содействию желательной информации и препятствию нежелательной информации). В настоящем документе будут часто использоваться термины "эпидемия", "инфекция", т.п.) подходящие для описания распространения нежелательной информации. Однако такой эпидемиологический язык относится как к желательной, так и к нежелательной информации, если не оговорено противного; этот язык используется только для удобства.

Существует множество моделей эпидемического распространения. В возможно наипростейшем классе подобных моделей каждому узлу присваивается только одно из двух возможных состояний: "неинфицированный" или "инфицированный". Если узел незаражен ("восприимчив"), узел полагается подверженным заражению любым зараженным соседним узлом. Соответственно, если узел заражен, узел остается в этом состоянии на протяжении эксперимента и сохраняет способность заразить любой соседний с ним узел. Конечно, за определенный промежуток времени узлы становятся "устойчивыми" к инфекции: человек вырабатывает антитела, машина получает антивирусное программное обеспечение, сплетни устаревают, или новшество становится устаревшим. Настоящая заявка сосредоточена на более коротком промежутке времени, так что состояние приобретенного иммунитета может быть проигнорировано. Данная модель распространения носит техническое обозначение "SI" (Susceptible or Infected, Восприимчивый или Зараженный), поскольку узел может находиться только в двух состояниях: восприимчивом и зараженном.

Поскольку распространение происходит по связям сети, очевидно, что топология сети имеет глубокое влияние на процесс распространения. В частности полагается, что лучшее понимание распространения приходит с точки зрения, основанной на образе всей сети, и на понимании структуры сети. В более ранней работе [1] был представлен подход к анализу структуры сети, применимый к любой сети с симметричными (ненаправленными) связями. Было также предложено, что анализ структуры сети должен быть полезен для понимания распространения по такой сети. Недавно в работе [2] авторами была разработана детальная частично количественная теория процесса распространения в таких сетях. Теория полностью основывается на структурном анализе. Настоящее изобретение обращается к вопросу об активной разработке или управлении сетями с целью управления (содействия или препятствия) распространению. Предложенный анализ предлагает ясные решения для управления распространением в обоих указанных смыслах.

Данный подход отступает от предшествующих работ в том, что сосредотачивается как на временном, так и на пространственном развитии распространения эпидемии. Пространственное разрешение не является микромасштабным, а скорее находится на уровне "областей" - связных подграфов с примерно одинаковой способностью к распространению. Более традиционные подходы, описанные в [4], начинаются с "однородной" аппроксимации, при которой каждый узел может заразить любой другой узел с некоторой вероятностью, в любой момент времени. О таком подходе можно сказать, что он не имеет сетевой перспективы; или можно сказать, что такой подход постулирует граф с чрезвычайно хорошей однородностью, такой как случайный граф высокого порядка или полный граф. В обзоре Ньюмана [4] также обсуждается более поздняя работа, включающая перспективы сетей. Вся подобная работа основывается на свойствах всего графа, таких как распределение порядков узлов; эти подходы также сосредотачиваются либо на получении результатов для всего графа или во времени [5, 6], либо сосредотачиваются на инфицированной части на большом промежутке времени [7]. Последний вопрос, несомненно, интересен только для моделей, превосходящих по сложности модель SI; в самом деле, основная часть работы направлена на поведение модели SIS (Susceptible, Infected, Susceptible again, Восприимчивый, Зараженный, Вновь восприимчивый), в которой узлы перестают быть инфицированными через определенное время, и вновь становятся восприимчивыми, или модели SIR (Susceptible, Infected, Refractory, Восприимчивый, Зараженный, Устойчивый), в которой узлы после избавления от инфекции проходят период устойчивости. Наконец, можно отметить, что работа, анализирующая только свойства всего графа, не может предоставить тех характерных улучшений конструкции, которые осуществлены в настоящем изобретении.

Брауэр [8] исследовал модель SI для случая рождения и гибели узлов (организмов, в особенности людей). Из-за добавления этих динамических свойств постоянный уровень заражения не обязательно равен 100%. Эта работа использует однородную аппроксимацию, что порождает парные обыкновенные дифференциальные уравнения. Поэтому данная работа также не может предложить локальные, характерные улучшения конструкции, подобные включенным в настоящее изобретение.

Наиболее близкой является работа Ванга и др. [9]. В этой работе рассматривается модель SIS, в которой узлы могут "излечиваться"; однако модель основана на полностью микромасштабном взгляде на сеть. Действительно, рассматриваемый в данной модели оператор, эволюционирующий во времени, совпадает с разработанным авторами настоящей статьи в [2] с двумя отличиями. Одно заключается в добавлении элемента "излечение". Этот элемент представляет собой кратное единичной матрицы, и тем самым не изменяет доминирующий собственный вектор, который остается вектором матрицы смежности А. Поскольку рассматривается модель SIS, долговременная доля заражения не является очевидной и должна быть найдена. Второе отличие от оператора эволюции во времени в работе Ванга и др. заключается в том, что Ванг и др. пренебрегают перекрестными членами, то есть теми, которые возникают в результате множественных передач на зараженный узел. Эта аппроксимация применима для низкого уровня заражения, хотя, как будет отмечено позже, указанная аппроксимация может оказаться подходящей даже при большом уровне заражения. Ванг и др. сообщают о моделировании, поддерживающем это утверждение.

Отметим использование в настоящей работе, как и в работе Ванга и др., полной матрицы смежности А при моделировании эволюции инфекции во времени. Тем самым рассуждения в настоящей работе начинаются с макромасштабного подхода. Однако внимание в настоящей работе будет вскоре обращено на "мезомасштабную" картину, в которой имеет смысл и полезно говорить об областях и их свойствах. Насколько известно, настоящая работа в этом отношении является уникальной. Эта картина областей является основой для способов (улучшения конструкции сетей), составляющих основу настоящего изобретения.

Раскрытие изобретения

Задачей настоящего изобретения является создание способа улучшенного распространения информации по сети и соответствующего способа с противоположным назначением, а именно препятствия распространению вредоносной информации по сети.

Эти задачи решаются при помощи способов, охарактеризованных в формуле изобретения. В своем первом аспекте настоящее изобретение предлагает способ содействия распространению информации или физического потока по сети, причем упомянутая сеть включает в себя некоторое число узлов сети, соединенных связями, содержащий следующие операции:

отображение топологии сети;

вычисление значений силы связей между узлами;

вычисление индекса центрированности собственных векторов для всех узлов на основе указанных значений силы связи;

определение узлов, имеющих локальные максимумы индекса центрированности собственных векторов (ЦСВ), как центральных узлов;

группирование узлов в областях, окружающих каждый центральный узел;

отличающийся тем, что включает в себя соединение, по меньшей мере, одного узла с высоким индексом центрированности собственных векторов в первой области, по меньшей мере, с одним узлом с высоким индексом центрированности собственных векторов во второй области.

Во втором аспекте изобретение предлагает способ распространения информации или физического потока по сети, отличающийся тем, что включает в себя добавление, по меньшей мере, одного нового узла и соединение, по меньшей мере, одного существующего узла с высоким индексом центрированности собственных векторов в каждой из первой и второй областей с указанным новым узлом.

В своем третьем аспекте изобретение предлагает способ предотвращения распространения информации или физического потока в сети, отличающийся тем, что осуществляется прививка, по меньшей мере, одного узла с высоким индексом центрированности собственных векторов путем блокирования передачи нежелательной информации по всем связям по направлению к указанному узлу и/или от него.

В своем четвертом аспекте изобретение предлагает способ предотвращения распространения информации или потока данных по сети, причем указанный способ отличается тем, что осуществляется прививка, по меньшей мере, одной связи с высоким индексом центрированности собственных векторов, соединяющей две области, путем блокирования передачи нежелательной информации по указанной связи.

Краткое описание чертежей

Для лучшего понимания изобретение далее будет описываться в деталях со ссылками на сопровождающие чертежи, на которых:

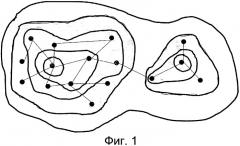
На фиг.1 представлена схематичная диаграмма сети с точки зрения топографии так, как она используется в настоящем раскрытии изобретения, с двумя "горами" (областями).

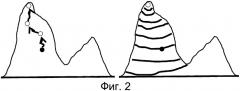
На фиг.2 представлено схематичное изображение эпидемического распространения в одной области. Две области на фиг.1 теперь рассматриваются со "стороны", так, как если бы они действительно представляли собой горы.

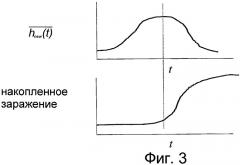
На фиг.3 представлено схематичное изображение развития заражения.

На фиг.4 представлено схематичное изображение соединения двух узлов с высоким индексом ЦСВ в различных областях при помощи связи.

На фиг.5 представлено схематичное изображение соединения центральных узлов при помощи связи.

На фиг.6 представлено схематичное изображение процедуры прививки центральных узлов в областях.

На фиг.7 представлено схематичное изображение процедуры прививки кольца узлов (с центром в центральном узле области), находящихся в одном шаге от центра области.

На фиг.8 представлено схематичное изображение процедуры прививки мостовых узлов с высоким индексом ЦВС.

На фиг.9 представлено схематичное изображение процедуры прививки мостовой связи с высоким индексом ЦВС.

На фиг.10 представлено схематичное изображение двух различных способов соединения двух подмножеств узлов. В способе А все узлы в одном множестве соединены со всеми узлами в другом множестве. В способе В добавляется дополнительный узел, и этот узел соединен со всеми или некоторыми узлами в каждом подмножестве узлов. Новый узел имеет топологию в форме звезды.

На фиг.11 представлено схематичное изображение двух различных способов соединения множеств центральных узлов. В способе А все центральные узлы соединены со всеми остальными центральными узлами. В способе В добавлен дополнительный узел, и этот узел соединен со всеми или некоторыми центральными узлами. Новый узел имеет топологию в форме звезды.

Осуществление изобретения

1. Топография из топологии.

Существенной особенностью настоящего подхода к анализу структуры сети является определение меры центральности для каждого узла сети. На самом деле существует множество различных мер центральности, большинство которых происходят из социальных наук [10]. Намерение авторов состояло в нахождении меры центральности, подразумевающей связность. Более того, было желательно найти не чисто локальное понятие связности. То есть желательно найти определение связности (центральности) для узла i, сообщающее некоторую информацию о соседних с узлом i узлах. Предположительно, такое понятие центральности может быть полезно для определения хорошо связанных кластеров в сети, и, основываясь на этом, для понимания распространения по той же сети.

Стратегия заключается в выборе центрированности собственных векторов [11] в качестве полезной меры связности. Центрированность собственных векторов (ЦСВ) обладает желательным свойством гладкости как меры на графе (или сети; эти термины взаимозаменяемы), поскольку ЦСВ зависит от свойств соседних узлов данного узла, а не только от самого узла. Это контрастирует с соответствующим свойством «порядок центрированности», который просто подсчитывает исходящие из узла связи, и тем самым связность узла является полностью локальной.

Подробно исследуем эту разницу. Начнем с порядка центрированности. Он измеряет "важность", или связанность, узла при помощи подсчета соседних узлов. Следовательно, относительная центрированность узла i является порядком данного узла, равного k_i. Ясно, что эта величина полностью локальна: заданный узел может иметь очень высокую относительную центрированность, и между тем все его соседние узлы могут иметь очень низкую относительную центрированность - отсутствует связь между данной величиной для узла и его соседних узлов. Индекс центрированности собственного вектора выглядит (по меньшей мере, словесно) только слегка видоизмененным. Для нахождения ЦСВ узла также необходимо подсчитать соседние узлы этого узла, но при этом необходимо взвесить центрированность (ЦВС) соседних узлов. То есть важно не только, сколько людей ты знаешь, но и кого ты знаешь. Математически это выражается формулой

Здесь е_i обозначает ЦСВ узла i, и j=nn(i) означает сумму по всем ближайшим соседним узлам узла i. Данное определение, несомненно, взаимное - центрированность узла зависит только от центрированности соседних узлов, однако их центрированность также зависит от центрированности данного узла. Однако уравнение (1) легко решается для нахождения ЦСВ, если во взвешенную сумму включена константа (const). Более того, предполагая только связность графа и симметричность соединений, можно сказать, что ЦСВ принимает только положительные значения (хотя значения могут быть "практически нулевыми" для крайних узлов).

Тем самым ЦСВ зависит не только от числа соседних узлов, но и от более широких вопросов, таких как число соседних узлов у соседних узлов и т.п. На самом деле ЦСВ узла зависит от всего графа. Однако для целей настоящего обсуждения более существенны две вещи: (i) ЦСВ несомненно измеряет связность некоторым нелокальным образом, и (ii) в связи со свойством (i) значения ЦСВ узлов, лежащих на любом заданном пути на графе, не изменяются случайно и произвольно. То есть выражение (1) вынуждает ЦСВ любого узла быть положительно связанным с ЦСВ его соседних узлов. Можно перефразировать это следующим образом: ЦСВ "гладкая" при перемещении по графу. Более точное математическое описание этой "гладкости" можно найти в [1].

Гладкость ЦСВ позволяет рассуждать в терминах "топографии" графа. То есть в случае, если узел обладает высокой ЦСВ, содержащая узел область также обладает достаточно высокой ЦСВ (из гладкости). Можно представить ЦСВ как гладко меняющуюся "высоту", с горами, впадинами, вершинами и т.п. Следует быть осторожным с тем, что все стандартные понятия топографии предполагают непрерывность описываемой топографией волнистой поверхности (и обычно двухмерность, как земная поверхность). Граф, с другой стороны, не непрерывен; также граф обычно не обладает четким соответствием с дискретной версией d-мерного пространства для любого d. Тем самым следует осторожно пользоваться топографическими идеями. Тем не менее, топографические идеи будут часто использоваться как вспомогательные средства для интуиции. Определения будут стимулированы данным интуитивным рассмотрением, однако будут математически точными и подходящими для случая дискретной сети.

Сначала будет определена "вершина". Вершиной называется точка, которая выше всех своих соседних точек - такое определение может быть применено неизменным к случаю дискретной сети. То есть, если ЦСВ узла выше ЦСВ любого из соседних узлов (так что наблюдается локальный максимум ЦСВ), этот узел называется центром, или центральным узлом. Затем известно существование горы для каждой вершины. Эти горы будут называться областями и играют существенную роль в настоящем рассуждении. То есть каждый не являющийся центром узел должен либо принадлежать одной из областей с некоторым центром, либо лежать на "границе" между областями. Тем самым определение области позволит получить способ разбиения сети на хорошо соединенные кластеры (области).

Предпочтительное определение принадлежности к области следующее: все узлы, у которых путь наискорейшего подъема оканчивается в одной точке локального максимума, принадлежат одной области. То есть определение принадлежности к области для данного узла заключается в нахождении наиболее высокого соседнего узла и определения, к какой области принадлежит этот узел. Все лежащие на этой цепочке узлы принадлежат области с данным центром. Также каждый узел принадлежит только одному центру, что исключает маловероятное событие нахождения узла, у которого два или большее количество наиболее высоких соседних узлов обладают одинаковым индексом ЦВС, но принадлежат различным областям.

Наконец обсуждается идея "долин" между регионами. Грубо говоря, долина определяется топографически отсутствием принадлежности к склонам, между которыми она находится. Тем самым согласно определению области ни один узел не лежит на равнине. Тем не менее, полезно рассматривать "пространство" между горами - в конце концов, это "пространство" соединяет области и тем самым играет важную роль в распространении. Данное "пространство равнины" обычно состоит исключительно из межобластных соединений. Данные межобластные связи в дальнейшем называются мостовыми связями, и любой узел, лежащий в точности на границе, может рассматриваться в качестве мостового узла.

На фиг.1 предложено наглядное представление перечисленных выше идей. Представлен простой граф с 16 узлами. Представлены топографические контуры равной высоты (равной ЦСВ). Два центра и соответствующие им горы (области) легко различимы на фигуре. Фигура настойчиво указывает на то, что две области, как определено настоящим анализом, внутренне связаны лучше, чем между собой. Более того, согласно фигуре правдоподобно, что распространение (например, вируса) гораздо легче произойдет внутри области, чем между областями. Тем самым фиг.1 наглядно выражает две задачи, которые желательно достичь при помощи ЦСВ: (i) обнаружить хорошо соединенные кластеры; и (ii) понять процесс распространения.

2. Топография и эпидемическое распространение

Для понимания распространения с сетевой точки зрения желательно некоторым образом оценить узлы сети с точки зрения "силы распространения". То есть определить, что одни узлы играют важную роль в распространении, в то время как другие играют менее важную роль. Для понимания можно представить сеть в форме звезды: центр звезды является критическим для распространения инфекции по сети; в то время как крайние узлы полностью неважны, обладая единственным свойством (общим для всех узлов) способности быть зараженными.

Несомненно, случай топологии звезды дает очевидный ответ на вопрос: какие узлы играют важную роль в распространении (имеют высокую силу распространения). Тем самым встает вопрос: как можно создавать одинаково осмысленные ответы для общих и сложных топологий, где ответ не так очевиден. В этом разделе будет предложен и разработан выраженный в качественной форме ответ на данный вопрос.

Основное предположение (А) просто и может быть выражено одним предложением:

Центрированность собственных векторов является хорошей мерой силы распространения. (А)

Данная идея была исследована экспериментально и теоретически [2]. Далее последует перечисление качественных аргументов в поддержку предположения (А); затем будут дополнительно исследованы следствия данного предположения. Будет показано, как может быть разработана достаточно детальная картина распространения эпидемии по сети, основываясь на предположении (А) и разработанном авторами структурном анализе, одним словом, основываясь на идеях, воплощенных на фиг.1.

Во-первых, как упомянуто выше, поскольку ЦСВ узла зависит от ЦСВ соседних узлов, изменение значения ЦСВ по сети можно рассматривать как "гладкое изменение". То есть узел с высокой ЦСВ не может быть окружен узлами с очень низкими ЦВС. Конечно, верно, что ЦСВ коррелирует с более простыми мерами центральности, а именно с порядком узла. На самом деле можно сказать, что принципиальная разница между этими мерами заключается в принудительной гладкости ЦСВ по определению самой ЦСВ, в то время как центрированность порядка узла не обладает этим свойством [12]. Однако эта разница может быть нетривиальной. Например, узел с высоким порядком, окруженный большим числом крайних узлов и слабо соединенный с основной массой большой и связной сети, будет иметь низкую ЦВС, несмотря на высокий порядок. Идея состоит в чувствительности ЦСВ к свойствам окрестности, в то время как у порядка узла такая чувствительность отсутствует.

Тем самым, коротко говоря, не существует изолированных узлов с высокой ЦВС. То есть узел с высоким значением ЦСВ находится в области с высоким значением ЦСВ. Однако могут существовать относительно изолированные узлы с низким значением ЦВС, поскольку такая ситуация является самоподдерживающей. Узлы с низким значением ЦСВ могут быть изолированы в смысле обладания малым числом соседних узлов; однако в этом случае соседние узлы все равно не будут иметь большого значения ЦВС. Теперь, если считать основное предположение (А) верным, то не существует изолированных узлов с большой силой распространения. Вместо этого существуют окрестности с большой силой распространения.

Предположим, далее, что инфекция достигла узла с умеренной силой распространения. Предположим также, что данный узел не является локальным максимумом ЦВС; вместо этого у данного узла есть соседний узел или узлы с большей силой распространения. Такое же замечание применимо к этим соседним узлам, до момента достижения одним из узлов локального максимума ЦВС/силы распространения.

Теперь, учитывая существование окрестностей, распространение может быть обсуждено в терминах окрестностей вместо обсуждения в терминах отдельных узлов. Из значения силы распространения следует, что характеризуемая большей силой распространения окрестность будет иметь большую скорость распространения, чем окрестность с низкой силой распространения. Более того, можно отметить гладкое соединение этих окрестностей с высокой и низкой силой распространения с окрестностями со средней силой распространения (и скоростью распространения).

Из всего вышесказанного следует, что при начале заражения в окрестности с низкой силой распространения заражение стремится распространиться в окрестность с более высокой силой распространения. То есть распространение проходит более быстро в направлении окрестности с высокой силой распространения, поскольку в таких окрестностях распространение происходит более быстро. Затем, после достижения окрестности с максимальной силой распространения, уровень заражения также достигает максимума (по времени). Наконец, при насыщении окрестности с высокой силой распространения заражение двигается вспять "под уклон", распространяясь во все "направления" от почти полностью насыщенной окрестности с высокой силой распространения и насыщая окрестности с низкой силой распространения.

Можно отметить естественную пригодность данного рассуждения к топографической картине топологии сети. Переводя предыдущий параграф на язык топографической картины, получается следующее: заражение склона стремится подняться вверх, и уровень заражения растет с высотой. Вершина горы, по ее достижении, быстро подвергается заражению; и затем зараженная вершина эффективно заражает все оставшиеся прилегающие склоны. Наконец, с гораздо меньшей скоростью происходит заражение подножья горы.

На фиг.2 графически выражены перечисленные идеи. Фигура показывает пример с двумя областями по фиг.1, но рассматриваемый со "стороны" - как если бы узел действительно обладал высотой. Начальное заражение возникает в отмеченном черным узле в левой области. Затем инфекция распространяется в первую очередь вверх с увеличивающимся уровнем заражения по мере возрастания "высоты" (=ЦВС, которая определяет согласно предположению силу распространения). Распространение инфекции достигает максимального уровня при достижении центральных узлов области; после этого инфекция "спускается" и заражает оставшуюся часть области. Можно отметить, что данная качественная картина хорошо соответствует различным стадиям классической S-образной кривой инновационной диффузии [13]. Начальная гладкая часть кривой отражает начальное заражение в низких окрестностей, во время данного периода инфекция медленно поднимается в гору. S-образная кривая набирает силу по мере достижения инфекцией более высоких частей горы. Затем наступает период быстрого роста в процессе насыщения вершины горы, одновременно с насыщением склонов. Наконец, уровень заражения замедляется по мере заражения низко лежащих окрестностей.

Перечисленные идеи вновь обобщаются на чертеже. На фиг.3 демонстрируется типичная S-образная кривая, представляющая заражение, в том случае (похожем на рассматриваемый в данной работе), если получение иммунитета невозможно. Над S-образной кривой представлена ожидаемая центрированность вновь зараженных узлов по мере прохождения времени. Согласно вышеперечисленным аргументам до заражения наиболее центральных узлов заражено относительно малое число узлов - даже при стабильно возрастающем фронте заражения. Тем самым фиг.3 левее пунктирной линии соответствует левой части фиг.2; аналогичным образом соответствуют правые части фигур.

Может возникнуть следующее возражение о простоте картины. Настоящая картина представляет S-образную кривую для одной горы. Тем не менее, известно, что сеть состоит из нескольких областей (гор). Тем самым возникает вопрос о причине возникновения S-образной кривой для сети с несколькими областями.

Предоставленный в данной работе ответ говорит о том, что подобные сети не обязательно проявляют S-образную кривую. То есть приведенные в настоящем рассуждении доводы указывают на наличие S-образной кривой для одной области, образованной вокруг локального максимума ЦВС. Затем, предполагая принадлежность узла единственной области, согласно предпочтительному правилу определения принадлежности области совместная кривая заражения представляет собой сумму кривых заражения для каждой области. Эти кривые для единственной области имеют S-образную форму. Например, в случае начала заражения на крайнем узле, прилежащем только к одной области, данная область может подвергнуться заражению гораздо раньше близлежащих областей. С другой стороны, в случае начала заражения в долине, прилежащей к нескольким вершинам, все эти вершины могут подвергнуться всплеску заражения одновременно, результатом чего окажется сумма примерно синхронизированных S-образных кривых, что в результате даст одну S-образную кривую.

Далее подведены итоги обсуждения и перечислены выводы из данной качественной картины.

а. Каждая область проявляет S-образную кривую.

b. Количество появлений возрастаний/плато на кумулятивной кривой всей сети может превышать единицу; однако данное количество не может превышать количество областей в сети.

с. При выполнении предположения о том, что начальное заражение начинается не в центральном узле (что является типичным случаем), для каждой области рост заражения вначале будет медленным.

d. При выполнении того же предположения, для каждой области начальный рост заражения будет проходить в сторону более высокого индекса ЦСВ.

е. Для каждой области при достижении заражением окрестности с высокой центрированностью рост замедляется.

f. Наблюдаемым следствием (е) является заражение центрального узла любой области во время или после, но никак не до замедления.

g. Для каждой области конечная стадия роста (насыщение) характеризуется низкой центрированностью.

3. Математическая теория

В работе [2] авторами была разработана математическая теория для выраженных в настоящей работе качественных идей. Работа [2] фокусируется на двух аспектах, которые в настоящей работе будут просто резюмированы.

Определение силы распространения

Первая задача заключается в попытке измерить и сделать точным предположение (А). Поскольку предположение (А) соотносит два количественных показателя - силу распространения и ЦСВ - где последнее точно определено, задача состоит в определении силы распространения и затем поиска зависимости между силой распространения и ЦСВ.

Подобная зависимость выглядит обоснованной. Соединенный с большим числом узлов с хорошей связностью узел должен обладать большей силой распространения и более высоким индексом ЦСВ, чем узел, соединенный с таким же числом узлов с меньшей связностью. В работе [2] авторами предложено точное определение силы распространения. Рассуждения проходят в два этапа: во-первых, определяется "коэффициент заражения" C(i, j) между любой парой узлов i и j. Этот коэффициент представляет собой взвешенную сумму всех нециклических соединений между i и j. Тем самым множество коротких путей между двумя узлами дадут им высокий коэффициент заражения. Данное определение симметрично, так что C(i, j)=C(j, i).

Затем определяется сила распространения узла i как сумма по всем узлам j коэффициентов заражения C(i, j) относительно узла i. До тех пор, пока граф остается связным, каждый узел будет иметь ненулевой коэффициент C(i, j) относительно любого другого узла, внося вклад в сумму. Каждый узел содержит одинаковое число слагаемых в сумме; однако узлы с большим числом высоких коэффициентов заражения, несомненно, будут обладать большей силой распространения.

Затем в работе [2] описывается способ установки связи между определением силы распространения и ЦСВ, в случае игнорирования ограничения на нециклические связи в определении. Сумма ограничивается всеми нециклическими путями, поскольку циклические пути не вносят вклад в распространение инфекции в SI случае. Данное ограничение делает получение аналитических результатов более сложным.

Математическая теория распространения SI

В работе [2] представлены точные уравнения распространения заражения, начинающегося в произвольном узле, в случае распространения SI. В связи с вероятностной моделью распространения через связи уравнения распространения заражения выражены стохастически в терминах вероятностей. Данные уравнения обычно не решаются, даже в невероятностном случае р=1. В последнем случае проблема вновь заключается в исключении всех нециклических путей. Однако авторами было проведено разложение по степеням р для временной эволюции вектора вероятностей заражения. Данное разложение показывает, что доминирующими составляющими являются составляющие, полученные простым применением матрицы смежности (т.е. игнорируя циклические пути, так как они длиннее и тем самым имеют более высокий порядок р). Затем устанавливается связь с ЦСВ: простое применение матрицы смежности дает веса (вероятности заражения), приближающиеся к распределению, пропорциональному ЦСВ. Тем самым получено некоторое подтверждение сделанного в настоящей работе утверждения о том, что на начальных стадиях заражения фронт заражения двигается по направлению к наибольшему индексу ЦСВ.

4. Проектирование и улучшение сетей

В данном разделе рассуждение коснется задачи проектирования сетей [14]. Представленные авторами идеи имеют ясные следствия для проектирования, заключающиеся в изменении топологии сети, одновременно для задачи предотвращения распространения вредоносной информации (такой как вирусы) и для задачи содействия распространению.

Способы улучшения распространения

Далее будут высказаны идеи в терминах топографической картины. Предположим, что задачей является проектирование или изменение сети с целью улучшения эффективности распространения. На основании предложенной в настоящей работе картины разумно предположить, что сеть с одной областью обладает оптимальной топологией для эффективного распространения. Тем самым, в настоящее изобретение включены четыре идеи, которые, как ожидается, улучшат поток информации по сети при помощи изменения данной (многообластной) сетевой топологии для придания ей большей схожести с одной областью:

1. Могут быть добавлены дополнительные мостовые связи между областями. Связи между узлами с высокими индексами ЦСВ в каждой области будут, вероятно, наиболее эффективны. Смотри фиг.4.

2. Как частный случай 1 могут быть соединены центры областей. Смотри фиг.5.

3. Подмножества узлов из разных областей могут быть соединены при помощи связующего узла, образуя конфигурацию в форме звезды. Смотри фиг.10В.

4. Все или некоторые центральные узлы могут быть соединены при помощи связующего узла, образуя конфигурацию в форме звезды. Смотри фиг.11В.

Идея 2 представляет собой "интенсивную" версию идеи 1. На самом деле, наиболее интенсивная версия идеи 2 заключается в соединении всех центров со всеми, тем самым образуя полный подграф между центрами. Полный подграф между 5 центрами представлен на фиг.11А. Альтернативой данной конструкции является вставка дополнительного связующего узла, отмеченного белым на фиг.11В, соединенного со всеми центральными узлами посредством одной связи для каждого узла. В некоторых случаях, когда физическая прокладка новых соединений является ресурсоемкой, а установка новых узлов осуществима, конструкция в форме звезды может быть более привлекательной, чем создание полного подграфа. При необходимости соединения n центров конструкция в форме звезды требует добавления всего n новых соединений и одного нового узла, в то время как конструкция полного подграфа требует добавления n(n-1)/2 новых соединений. Комбинации двух данных подходов также возможны; одно подмножество центров может быть соединено как полный подграф, в то время как другое подмножество может быть соединено при помощи связующего узла.

Однако подобные интенсивные подходы на практике могут оказаться сложными или невыполнимыми. В таком случае остаются общие идеи 1 и 3 построения большего числа мостов между областями. Однако нет причины выбирать наиболее интенсивный подход при реализации данной идеи. То есть: следует создавать мосты между узлами с высокой центрированностью на обеих сторонах и предпочтительно как можно больше. Проведенный авторами анализ настоятельно предлагает данную стратегию в качестве наилучшей для изменения топологии сети с целью улучшения распростране