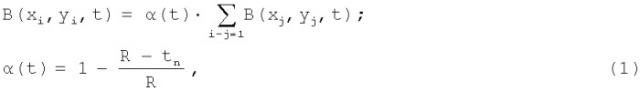Способ прогнозирования ав-блокады ii степени

Способ прогнозирования ав-блокады ii степени

Иллюстрации

Показать все

Реферат

Предлагаемое изобретение относится к кардиологии и может быть использовано в клинических и экспериментальных исследованиях как неинвазивный способ прогнозирования аритмии, в частности прогнозирования атриовентрикулярной (АВ) блокады сердца и для наглядного представления процесса распространения возбуждения в миокарде.

АВ-блокада сердца [1] вызвана синоатриальной дисфункцией и характеризуется аномальной координацией между предсердными и желудочковыми сокращениями. Выделяют атриовентрикулярную блокаду I степени (удлинение интервала между предсердными и желудочковыми сокращениями), II степени (увеличение числа сокращений предсердий по отношению к числу сокращений желудочков, происходящих из-за блокированного проведения некоторых из предсердных биений) и III степени (полное отсутствие координации между предсердными и желудочковыми ритмами).

Известен неинвазивный способ определения основных показателей миогемодинамики левого желудочка (ЛЖ) сердца, заключающийся в регистрации электрокардиограммы (ЭКГ), анализе информационных показателей (ИП) ЭКГ, регистрации флюорографии, анализе информационных показателей флюорографии и дальнейшем синтезе модели сердца человека и определении показателей миогемодинамики сердца [2].

К недостаткам известного способа определения основных показателей миогемодинамики сердца относятся:

- отсутствует возможность анализа ИП ЭКГ и оценки состояния сердца пациента под нагрузкой;

- отсутствует возможность прогнозирования АВ-блокады II степени.

Наиболее близким по достигаемому результату к предлагаемому изобретению является способ моделирования и визуализации распространения возбуждения в миокарде, заключающийся в том, что осуществляют регистрацию электрокардиограммы, регистрацию флюорографии сердца пациента, анализ информационных показателей электрокардиограммы, определение по снимкам геометрических параметров сердца пациента, синтез модели сердца пациента, моделирование распространения возбуждения в миокарде, затем по результатам моделирования - визуализацию распространения возбуждения в миокарде [3].

К недостаткам известного способа моделирования и визуализации распространения возбуждения в миокарде относятся

- отсутствует возможность анализа ИП ЭКГ и оценки состояния сердца пациента под нагрузкой;

- отсутствует возможность прогнозирования АВ-блокады II степени.

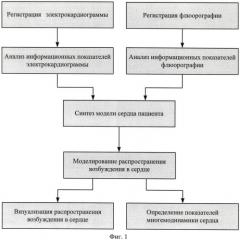
На фигуре 1 приведена схема алгоритма, реализующего известный способ моделирования и визуализации распространения возбуждения в миокарде.

Действительно, из анализа фигуры 1 и описания известного способа моделирования и визуализации распространения возбуждения в миокарде следует, что эффект достигается только за счет визуализации и моделирования состояния сердца пациента по результатам анализа кардиографической информации. Именно наглядное представление диагностической информации об электрической активности сердца в течение кардиоцикла является принципиальной отличительной особенностью известного способа моделирования и визуализации распространения возбуждения в миокарде.

Однако, по мнению авторов, такое представление диагностической информации для оценки состояния сердца пациента является недостаточным. Врачу необходима информация о степени «тренированности» сердца пациента [4]: например, условия возникновения АВ-блокады II степени, что позволяет оценить возможности сердца по отношению к нагрузкам, т.е. какие нагрузки допустимы, а каких следует избегать.

Изобретение направлено на расширение функциональных возможностей кардиологического исследования за счет оценки степени «тренированности» сердца пациента путем прогнозирования АВ-блокады II степени.

Это достигается тем, что в способе моделирования и визуализации распространения возбуждения в миокарде, заключающемся в том, что осуществляют регистрацию электрокардиограммы, регистрацию фронтального и левобокового флюорографических снимков сердца пациента, анализ информационных показателей электрокардиограммы, определение по снимкам геометрических параметров сердца пациента, синтез модели сердца пациента, моделирование распространения возбуждения в миокарде, затем по результатам моделирования - визуализацию распространения возбуждения в миокарде, дополнительно осуществляют регистрацию электрокардиограммы под нагрузкой, определение параметров модели распространения возбуждения в миокарде, построение кривой восстановления сердца пациента и определение частоты сердечных сокращений - ЧСС, при которой возможна АВ-блокада II степени.

При этом регистрацию электрокардиограммы под действием нагрузки осуществляют до достижения частоты сердечных сокращений, определяемой по формуле

ЧСС=(220-возраст)·0,75,

а для больных ишемической болезнью сердца:

ЧСС=(220-возраст)·0,5.

При этом определение параметров модели распространения возбуждения в миокарде осуществляют по формулам

V=S/t,

R=λ_cp/V=(λ_cp·t)/S,

где V - скорость распространения возбуждения в миокарде, S - путь распространения возбуждения по проводящей системе сердца, t - время распространения возбуждения в миокарде, R - рефрактерность миокарда пациента, λ_ср - средняя длина волны распространения возбуждения в миокарде.

При этом кривую восстановления сердца пациента находят путем аппроксимации результатов моделирования функцией вида

где SH - интервал времени от начала импульса возбуждения в синусовом узле до начала ответного импульса в клетках пучка Гиса, t_s - интервал времени между импульсами возбуждения синусового узла, α и β - положительные константы, N - наименьшее целое число, такое, что N·t_s-SH_i-1>R.

При этом определение частоты сердечных сокращений, при которой возможна АВ-блокада II степени, осуществляют по формуле

ЧСС_{блокада}=60000/t_{s(блокада)},

где t_{s(блокада)} - интервал времени в миллисекундах между импульсами возбуждения синусового узла, при котором H/L<1, где L - число импульсов возбуждения в синусовом узле для заданного t_s и различных SH, Н - число ответных импульсов в клетках пучка Гиса для заданного t_s и различных SH, при этом Н=1, L=N_i=((R+SH_i-1)/t_s)+1 при N₁=N₂=…=N_i, H=i, L=N₁+N₂+…+N_i при N₁≠N₂≠…≠N_i.

Введенные действия с их связями проявляют новые свойства, которые позволяют на основе моделирования процесса распространения возбуждения в миокарде проследить динамику поведения сердечно-сосудистой системы (ССС) в зависимости от нагрузки, т.е. выявить АВ-блокаду II степени. Прогнозирование АВ-блокады II степени осуществляют с привязкой к показателям электрической активности сердца (ЭАС) при различной нагрузке.

Генезис АВ-блокады II степени обусловлен удлинением абсолютного и относительного рефрактерного периодов в атриовентрикулярном соединении. При этой блокаде проводимость в атриовентрикулярном соединении прогрессивно ухудшается от сокращения к сокращению. Такое ухудшение атриовентрикулярной проводимости продолжается до тех пор, пока атриовентрикулярное соединение становится не в состоянии провести очередной импульс к желудочкам. Это приводит к выпадению сокращения желудочков. На ЭКГ постепенное ухудшение атриовентрикулярной проводимости проявляется в прогрессирующем удлинении интервала PQ от комплекса к комплексу. Исходный интервал PQ может быть нормальным или удлиненным. В тот момент, когда атриовентрикулярный узел становится не в состоянии провести очередной импульс к желудочкам, на ЭКГ регистрируется только зубец Р, обусловленный возбуждением предсердий, а желудочковый комплекс QRST выпадает. Выявляется длительная пауза. После паузы наблюдается наименьший интервал PQ. Затем цикл повторяется. Число сокращений желудочков при блокаде II степени всегда меньше числа зубцов Р, так как часть предсердных зубцов блокируется. При этой блокаде говорят об атриовентрикулярной блокаде 3:2, 4:3 и т.д., указывая в числителе число предсердных зубцов Р, а в знаменателе - число комплексов QRS.

В основе предлагаемого способа лежит прогнозирование сердечного ритма, заключающееся в экстраполяции результатов анализа ИП ЭКГ и определении по флюорографическим снимкам геометрических параметров сердца, моделирование распространения возбуждения в миокарде, построение функции кривой восстановления сердца пациента и определение частоты сердечных сокращений - ЧСС, при которой возможно выпадение сокращений желудочков. При этом по результатам анализа ЭКГ до и после нагрузки определяются временные отсчеты начала и окончания процессов деполяризации и реполяризации участков проводящей системы сердца. Отличительной особенностью предлагаемого способа является то, что на основе этих временных отсчетов определяются параметры для τ-модели распространения возбуждения в миокарде. При увеличении физической нагрузки частота активации синусового узла увеличивается. Поскольку скорость распространения импульсов возбуждения остается неизменной, то возникают предпосылки АВ-блокады II степени. Очевидно, что при увеличении нагрузки интервал PR есть убывающая функция предшествующего интервала PR, и это обстоятельство с учетом постоянства абсолютного и относительного рефрактерного периодов в атриовентрикулярном соединении используется для определения условия возникновения АВ-блокады II степени. По результатам моделирования строится график функции Кантора, характеризующий степень «тренированности» ССС.

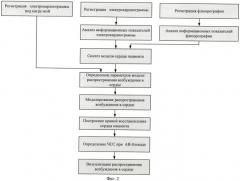
На фигуре 2 приведена схема алгоритма, реализующего предлагаемый способ прогнозирования АВ-блокады II степени.

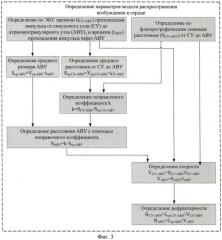
На фигуре 3 приведена схема алгоритма, реализующего определение параметров модели распространения возбуждения в миокарде.

На фигуре 4 приведена схема алгоритма, реализующего построение функции кривой восстановления сердца пациента.

На фигуре 5 приведена схема алгоритма, реализующего определение ЧСС при АВ-блокаде II степени.

На фигуре 6 приведена форма трансмембранного потенциала действия клетки миокарда в τ-модели Винера-Розенблюта [5].

На фигуре 7 приведена форма трансмембранного потенциала действия клетки миокарда в разных отделах сердца, где приняты следующие обозначения:

1 - синусовый узел;

2 - предсердие;

3 - атриовентрикулярный узел;

4 - пучок Гиса;

5 - ножки пучка Гиса;

6 - волокна Пуркинье;

7, 8 - левый желудочек.

На фигуре 8 приведена иллюстрация распространения волны возбуждения в миокарде на основе τ-модели.

На фигуре 9 приведена иллюстрация периодической стимуляции синусовым узлом сердечной мышцы.

На фигуре 10 приведены ЭКГ пациента до и после нагрузки:

а) ЭКГ до нагрузки;

б) ЭКГ после нагрузки.

На фигуре 11 приведены флюорографические снимки пациента.

На фигуре 12 приведена кривая восстановления ССС пациента.

На фигуре 13 приведен график динамики ССС пациента в зависимости от периода стимуляции синусовым узлом сердечной мышцы.

На фигуре 14 приведена иллюстрация визуализации распространения возбуждения в миокарде при атриовентрикулярной блокаде.

Как следует из анализа фигуры 2, в предлагаемом способе по данным анализа флюорографических снимков и ЭКГ до и после нагрузки осуществляется:

- определение геометрических параметров сердца пациента;

- определение изменения интервала PR;

- определение параметров модели;

- моделирование распространения возбуждения в миокарде, в результате которого определяются: интервал времени SH от импульса возбуждения синусового узла до начала ответного импульса в пучке Гиса и интервал времени HS от начала активности в пучке Гиса до момента поступления следующего импульса возбуждения синусового узла;

- построение функции кривой восстановления сердца пациента;

- определение частоты сердечных сокращений, при которой возможно выпадение сокращений желудочков.

Другими словами, прогнозирование АВ-блокады II степени осуществляется на основе моделирования процесса распространения возбуждения с учетом анализа кардиографической информации. При этом регистрация ЭКГ осуществляется в спокойном состоянии и под действием нагрузки до достижения частоты сердечных сокращений, определяемой по формуле

ЧСС=(220-возраст)·0,75,

а для больных ишемической болезнью сердца

ЧСС=(220-возраст)·0,5.

Определяются параметры модели, затем моделируется распространение возбуждения в миокарде; определяется функция кривой восстановления и прогнозируется динамика поведения ССС в зависимости от периода возбуждения предсердий, т.е. выявляются условия возникновения АВ-блокады II степени.

Для модели, описывающей распространение возбуждения в миокарде, определяются следующие параметры:

- скорость прохождения импульса от синусового узла до атриовентрикулярного узла и скорость прохождения импульса в атриовентрикулярном узле;

- длина волны в предсердиях и длина волны в атриовентрикулярном узле;

- рефрактерность миокарда пациента для участка от синусового узла до атриовентрикулярного узла и для атриовентрикулярного узла.

Для расчета вышеуказанных параметров по алгоритму, приведенному на фигуре 3, необходимо по данным ЭКГ и флюорографических снимков определить:

1. Время t_СУ-АВУ прохождения импульса возбуждения от синусового узла до атриовентрикулярного узла, как две третьих зубца Р ЭКГ [1].

2. Время t_АВУ прохождения импульса в атриовентрикулярном узле, которое соответствует последней трети зубца Р плюс первая половина сегмента PQ ЭКГ [1].

3. Расстояние S_СУ-АВУ от синусового узла до атриовентрикулярного узла.

4. Среднее расстояние S_{cp.СУ-АВУ} от синусового узла до атриовентрикулярного узла и средний размер S_cp.АВУ атриовентрикулярного узла по формулам

S_{ср.СУ-АВУ}=V_{ср.СУ-АВУ}·t_СУ-АВУ,

S_ср.АВУ=V_ср.АВУ·t_АВУ,

где V_{ср.СУ-АВУ} - средняя скорость прохождения импульса от синусового узла до атриовентрикулярного узла, V_ср.АВУ - средняя скорость прохождения импульса в атриовентрикулярном узле. Известно, что в стенках предсердий возбуждение распространяется со скоростью 30÷80 см/с [1], следовательно, V_{ср.СУ-АВУ} = 55 см/с. Скорость распространения возбуждения в атриовентрикулярном узле варьируются от 2 до 5 см/с [1], следовательно, V_ср.АВУ=3,5 см/с.

5. Поправочный коэффициент k, с помощью которого вычисляется размер атриовентрикулярного узла сердца пациента,

k=S_СУ-АВУ/S_{cp.СУ-АВУ},

S_АВУ=k·S_ср.АВУ

6. Скорость V_СУ-АВУ прохождения импульса от синусового узла до атриовентрикулярного узла и скорость V_АВУ прохождения импульса в атриовентрикулярном узле

V_СУ-АВУ=S_СУ-АВУ/t_СУ-АВУ,

V_АВУ=S_АВУ/t_АВУ

7. Рефрактерность миокарда пациента для участка от синусового узла до атриовентрикулярного узла R_СУ-АВУ и для атриовентрикулярного узла R_АВУ по формулам

R_СУ-АВУ=λ_{ср.СУ-АВУ}/V_СУ-АВУ,

R_АВУ=λ_ср.АВУ/V_АВУ,

где λ_ср - средняя длина волны распространения возбуждения в миокарде. Известно [1], что в предсердиях λ_{ср.СУ-АВУ}=12 см, в атриовентрикулярном узле λ_ср.АВУ=0,6 см.

Регистрация ЭКГ осуществляется в спокойном состоянии и под действием нагрузки, поэтому выбор времени t_СУ-АВУ и t_АВУ, которое необходимо взять для расчета рефрактерности, осуществляется по следующему алгоритму:

- время до нагрузки, если интервалы t_СУ-АВУ и t_АВУ до и после нагрузки увеличились;

- время под действием нагрузки, если интервалы t_СУ-АВУ и t_АВУ до и после нагрузки сократились;

- любое время, если интервалы t_СУ-АВУ и t_АВУ до и после нагрузки не изменились.

Результаты расчета параметров модели распространения возбуждения на основе анализа ЭКГ (см. фигуру 10) и флюорографических снимков (см. фигуру 11) приведены в таблице 1.

Таблица 1
Параметр	Значение до нагрузки	Значение под действием нагрузки
tСУ-АВУ [с]	0,114	0,050
tАВУ [с]	0,1115	0,0495
SСУ-АВУ [см]	5,83
SАВУ [см]	0,375
VСУ-АВУ [см/с]		116,6
VАВУ [см/с]		7,5
λср.СУ-АВУ [см]	12
λср.АВУ [см]	0,6
RСУ-АВУ [с]		0,103
RАВУ [с]		0,08

Далее выполняется моделирование распространения возбуждения в миокарде с помощью τ-модели Винера-Розенблюта, позволяющей описать процесс распространения возбуждения в проводящей системе сердца [5]. В модели Винера-Розенблюта постулируется, что возбудимая среда образована сетью из элементов (клеток миокарда), каждый из которых способен пребывать в трех состояниях - покоя, возбуждения и рефрактерности; переходы между состояниями осуществляются скачком, подчиняясь определенным правилам. В отсутствие внешних воздействий элемент неограниченно долго сохраняет состояние покоя. Внешним воздействием его можно перевести из этого состояния в состояние возбуждения. Пробыв определенное время τ в состоянии возбуждения, элемент переходит к состоянию рефрактерности, в котором он является невозбудимым. Состояние рефрактерности длится время R, по прошествии этого времени способность к возбуждению восстанавливается - элемент переходит в состояние покоя.

Значения трансмембранного потенциала действия (ТМПД) φ для каждого из трех возможных состояний клетки миокарда (см. фигуру 6) определяется следующим образом:

1. Возбуждение - τ, при этом потенциал мембраны φ_м>φ_м ^пор, клетка не возбудима, но может возбудить соседнюю клетку, находящуюся в покое.

2. «Рефрактерный» хвост - (R-τ), при этом потенциал мембраны φ_м ^п<φ_м<φ_м ^пор, клетка не возбудима и не может возбудить соседнюю клетку, находящуюся в покое.

3. Покой - при этом потенциал мембраны φ_м=φ_м ^п, в этом состоянии клетка может быть возбуждена соседней при условии, что трансмембранный потенциал действия соседней клетки выше значения порога рассматриваемой клетки.

Сравнение электрофизиологических данных (см. фигуру 7) и формы трансмембранного потенциала действия модели Винера-Розенблюта (см. фигуру 6) показывает, что в модели приняты следующие допущения:

- форма трансмембранного потенциала действия упрощена и близка к прямоугольному треугольнику;

- весь интервал R считается абсолютно рефрактерным.

Модель Винера-Розенблюта описывается уравнением работы клеточного автомата [5]

,

где α(t) - величина рефрактерности клетки миокарда; R - длительность интервала рефрактерности; t_n - длительность интервала покоя.

Волну возбуждения в модели Винера-Розенблюта можно представить в виде некоторой зоны, состоящей из n клеток, находящихся в рефрактерной фазе R, и двигающейся по области покоящихся клеток с постоянной скоростью V (см. фигуру 8). Скорость распространения возбуждения определяется соотношением, введенным Винером:

V=λ/R.

Из выражения (1), описывающего τ-модель, и соотношения Винера следует, что для перехода клетки миокарда в другое состояние необходимо знать состояния клетки и ближайших ее соседей.

Используя соотношение Винера и данные анализа ЭКГ, определяются параметры модели распространения возбуждения в проводящей системе сердца. Так как вариантов наборов параметров модели может быть несколько, для однозначной интерпретации результатов моделирования необходимо дополнительное условие, заключающееся в том, чтобы скорость распространения возбуждения до и после физической нагрузки оставалась неизменной: V_пок=V_нагр. Это условие обусловлено тем, что в автоволновой парадигме только параметры среды распространения возбуждения определяют скорость распространения возбуждения, и эта скорость не зависит от внешних по отношению к среде распространения возбуждения факторов. Поскольку скорость распространения возбуждения не зависит от внешних факторов, а частота активации синусового узла увеличивается при увеличении нагрузки на сердце, то возникают предпосылки для возникновения периодики Венкебаха. Сказанное иллюстрируется фигурой 9, показывающей периодическую стимуляцию синусовым узлом сердечной мышцы с интервалом времени t_s.

Импульс S_i с синусового узла вызывает возбуждение в желудочках после некоторой задержки SH_i. Длительность интервала SH_i является функцией времени от окончания предшествующего возбуждения до момента приложения импульса S_i. В этом случае интервал SH соответствует времени от начала импульса возбуждения в синусовом узле до начала ответного импульса в клетках пучка Гиса. Обозначив временной интервал между импульсами возбуждения синусового узла через t_s, получим

,

где С - искомая функция, которая в электрофизиологии сердца называется кривой восстановления.

Для нахождения функции С необходимо получить выборку последовательного изменения интервала SH от его предшествующего значения. С помощью τ-модели моделируется распространение возбуждения и определяются значения интервала SH при различной частоте возбуждения синусового узла.

Для определения условий возникновения АВ-блокады II степени используются в качестве параметров τ-модели показатели, приведенные в таблице 1. Результаты моделирования процесса распространения возбуждения в миокарде на основе аксиоматической модели Винера-Розенблюта приведены в таблице 2. Первому столбцу таблицы 2 соответствуют значения интервалов времени от начала импульса в синусовом узле до начала ответного импульса в пучке Гиса, а второму столбцу - интервал времени от начала активности в пучке Гиса до момента поступления следующего импульса возбуждения с синусового узла.

Таблица 2
Интервал времени от начала активности в пучке Гиса до момента поступления следующего импульса с синусового узла, (HS), мс	Интервал времени от импульса с синусового узла до начала ответного импульса в пучке Гиса, (SH), мс
486,52	88,75
475,29	89,625
444,59	87,857
410,15	89,643
388,44	89,107
377,2	91,143
351	88,304
345,76	89,732
311,31	90,161
295,59	88,661
260,4	89,821
246,17	89,804
225,21	88,571
209,48	90,875
194,51	91,768
175,04	90,982
160,82	92,571
151,08	94,089
144,34	91,25
132,36	93,821
124,13	93,75
119,63	97,125
117,39	100,25
112,15	95,268
100,17	103,91
99,418	99,54
96,423	97,857
85,94	101,79
82,945	107,3
76,955	106,16
73,96	110,7
71,714	103,93
64,226	117,13

Функция кривой восстановления сердца определяется по алгоритму, приведенному на фигуре 4, путем осуществления регрессионного анализа, исходными данными для которого являются полученные значения интервалов времени SH и HS. В данном случае была выбрана регрессионная модель, представленная экспоненциальной функцией вида

где SH_min, α, β - параметры регрессионной модели.

Для определения параметров регрессионной модели используется метод наименьших квадратов. Для результатов моделирования, приведенных в таблице 2, регрессионная модель представлена в виде

Графическая иллюстрация кривой восстановления представлена на фигуре 12.

Полученная в виде уравнения модель (2) проверяется на адекватность средствами регрессионного и корреляционного анализа [6]:

1. Теснота связи между величинами оценивается по величине корреляционного отношения

,

где σ² _у - общая дисперсия результативного признака, σ² _у - остаточная дисперсия, определяемая, исходя из уравнения регрессии.

Так , а ,

то индекс корреляции можно выразить как

Величина данного показателя находится в границах: 0≤R≤1, т.е. чем ближе к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии.

2. Коэффициент детерминации R² - величина, показывающая, какая часть общей вариации SH обусловлена вариацией SH_i-1.

3. Оценка качества построенной функции рассчитывается с помощью - критерия ошибки аппроксимации по формуле

.

4. Критерий Фишера F оценивает качество уравнения регрессии. Гипотеза Н₀ состоит в том, что уравнение регрессии и показатели тесноты связи статистически незначимы. Значение критерия Фишера F определяется по формуле

В процессе оценки адекватности модели (3) для интервалов SH из таблицы 2 получены значения вышеуказанных критериев, которые приведены в таблице 3.

Таблица 3
Коэффициент	Значение
Индекс корреляции R	0.977323
Индекс детерминации R2	0.955161
Ошибка аппроксимации	3,52%
Критерий Фишера F	468,6399

Анализ полученных критериев оценки адекватности модели (3) показывает, что:

- связь изменения интервала SH от его предшествующего значения сильная;

- полученная в виде уравнения модель (3) адекватна и 95,5% вариации интервала S-H объясняется вариацией его предшествующего значения;

- ошибка аппроксимации составляет 3,5% и не превышает 8-10%, что свидетельствует о хорошем качестве модели (3);

- табличное (критическое) значение критерия Фишера F при уровне значимости 0,05 составляет 4,28. Так как, наоборот, F_табл<<F_факт, то гипотеза Н₀ отвергается и делается вывод о статистической значимости и надежности уравнения модели (3).

После проверки модели (2) на адекватность интервал HS необходимо выразить через предшествующий интервал SH для прогнозирования АВ-блокады II степени. Тогда кривая восстановления будет представлена в следующем виде:

,

где t_s - интервал времени между импульсами возбуждения синусового узла, N - наименьшее целое число, такое, что N·t_s-SH_i-1>R.

Определение частоты сердечных сокращений (см. фигуру 5), при которой возможна АВ-блокада II степени, осуществляется по формуле

ЧСС_{блокада}=60000/t_{s(блокада)},

где t_{s(блокада)} - интервал времени в миллисекундах между импульсами возбуждения синусового узла, при котором возможна АВ-блокада II степени. Для определения t_{s(блокада)} необходимо итерировать полученное уравнение (4).

Интервал времени t_s между импульсами возбуждения синусового узла равен t_{s(блокада)}, если число ответных импульсов H в клетках пучка Гиса меньше числа импульсов возбуждения L в синусовом узле, т.е. H/L<1. Для определения H и L необходимо:

1. Задать интервал времени t_s между импульсами возбуждения синусового узла.

2. Рассчитать для заданного t_s количество стимулов по формуле

N_i-1=((R+SH_i-1)/t_s)+1,

откуда N взять как целое число.

3. Определить SH_i для заданного t_s и рассчитанного N_i-1 по формуле

4. Определить H и L, при этом H=1, L=N_i=((R+SH_i-1)/t_s)+1 при N₁=N₂=…=N_i; H=i, L=N₁+N₂+…+N_i при N₁≠N₂≠…≠N_i.

В случаях H/L<1, т.е. когда число ответных импульсов в клетках пучка Гиса меньше числа импульсов возбуждения в синусовом узле, констатируется выпадение сокращения желудочков. В случаях H/L=1 АВ-блокады II степени не будет, так как количество импульсов, пришедших от синусового узла в пучок Гиса, будет равно числу прошедших импульсов через него. Для определения ЧСС_{блокада} в качестве t_{s(блокада)} берется t_s при всех H/L<1.

Данный алгоритм повторяется при различных значениях интервалов времени t_s между импульсами возбуждения синусового узла. Для графического представления ритмов Венкебаха используется функция Кантора, называемая также «чертовой лестницей» [7], построенная по функции восстановления. На фигуре 13 приведен график функции Кантора для пациента с ЭКГ, приведенной на фигуре 10, и с флюорографическими снимками, приведенными на фигуре 11. Здесь показано отношение между числом проводимых биений и числом стимулов ρ, на интервале [0;1] как функция t_s. Анализ графика функции Кантора показывает, что при t_s=400 мс возникает ритм Венкебаха 2:1, где числитель - L, а знаменатель - Н, т.е. при частоте пульса 150 ударов в минуту возможно выпадение сокращения желудочков. На фигуре 13 наблюдаются классические ритмы Венкебаха вида N: N-1, а также более сложные их вариации.

Для визуализации процесса распространения возбуждения в миокарде используется изображение модели сердца пациента. На фигуре 14 показаны распределения трансмембранного потенциала действия по поверхности сердца, при АВ-блокаде II степени в отношении 2:1, соответствующие следующим стадиям возбуждения миокарда (слева направо сверху вниз):

- начало поляризации правого предсердия;

- полная поляризация правого предсердия, начало поляризации левого предсердия;

- атриовентрикулярная блокада желудочков;

- начало поляризации правого предсердия;

- полная поляризация правого предсердия, начало поляризации левого предсердия;

- окончание поляризации предсердий, начало поляризации желудочков от верхушки сердца;

- поляризация желудочков;

- окончание поляризации желудочков;

- начало деполяризации желудочков;

- деполяризация желудочков;

- окончание деполяризации желудочков.

Таким образом, на основе реалистичного трехмерного изображения модели сердца пациента, построенной по данным анализа электрокардиографии и флюорографии, рассмотрена визуализация распространения волны возбуждения при атриовентрикулярной блокаде желудочков.

Технико-экономический эффект, достигаемый при реализации предлагаемого способа, заключается в прогнозировании АВ-блокады II степени, что позволяет оценить степень «тренированности» сердца пациента.

Литература

1. Орлов В.Н. Руководство по электрокардиографии. - М.: Медицина, 1984, 528 с.

2. Патент РФ №2264786. Способ определения основных функциональных показателей миогемодинамики сердца /Бодин О.Н., Бурукина И.П., Митин А.А., Огоньков В.В., Митрошин А.Н., Бондаренко Л.А., Рудакова Л.Е. //Официальный бюллетень «Изобретения. Полезные модели». №33, 2005.

3. Решение о выдаче патента по заявке на изобретение №2007123430 от 19.12.2008. Способ моделирования и визуализации распространения возбуждения в миокарде /Бодин О.Н., Гладкова Е.А., Кузьмин А.В., Митрохина Н.Ю., Мулюкина Л.А., Строкова И.В.

4. Амосов Н.М. Раздумья о здоровье. М.: Молодая гвардия, 1979, 191 с.

5. Винер Н., Розенблют А. Проведение импульсов в сердечной мышце. //Кибернетический сборник, №3, ИЛ, 1961.

6. Тюрин Ю.Н., Макаров А.А. Анализ данных на компьютере /Под ред. В.Э. Фигурнова. - 3-е изд., перераб. и доп. - М.: ИНФРА-М, 2003, 544 с.

7. Александров П.С. Введение в теорию множеств и общую топологию. М.: Наука, 1997, 368 с.

Способ прогнозирования АВ-блокады II степени, заключающийся в том, что осуществляют регистрацию электрокардиограммы, регистрацию фронтального и левобокового флюорографических снимков сердца пациента, анализ информационных показателей электрокардиограммы, определение по снимкам геометрических параметров сердца пациента, синтез модели сердца пациента, моделирование распространения возбуждения в миокарде, затем по результатам моделирования - визуализацию распространения возбуждения в миокарде, отличающийся тем, что осуществляют регистрацию электрокардиограммы под нагрузкой до достижения частоты сердечных сокращений, определяемой по формуле ЧСС=(220-возраст)·0,75, а для больных ишемической болезнью сердца ЧСС=(220-возраст)·0,5, определение параметров модели распространения возбуждения в миокарде по формулам:V=S/t,R=λ_сp/V=(λ_сp·t)/S,где V - скорость распространения возбуждения в миокарде, S - путь распространения возбуждения по проводящей системе сердца, t - время распространения возбуждения в миокарде, R - рефрактерность миокарда пациента, λ_ср - средняя длина волны распространения возбуждения в миокарде, построение кривой восстановления сердца пациента осуществляют путем аппроксимации результатов моделирования функцией вида: , где SH - интервал времени от начала импульса возбуждения в синусовом узле до начала ответного импульса в клетках пучка Гиса; t_s - интервал времени между импульсами возбуждения синусового узла; SH_min, α и β - параметры модели распространения возбуждения в миокарде; N - наименьшее целое число, такое, что N·t_s-SH_i-1>R, определение частоты сердечных сокращений, при которой возможна АВ-блокада II степени, осуществляют по формуле ЧСС_{блокада}=60000/t_{s(блокада)}, где t_{s(блокада)} - интервал времени в миллисекундах между импульсами возбуждения синусового узла, при котором H/L<1, где L - число импульсов возбуждения в синусовом узле для заданного t_s и различных SH, Н - число ответных импульсов в клетках пучка Гиса для заданного t_s и различных SH, при этом H=1, L=N_i=((R+SH_i-1)/t_s)+1 при N₁=N₂=…=N_i, H=i, L=N₁+N₂+…+N_i при N₁≠N₂≠…≠N_i.