Способ определения коэффициента пуассона

Способ определения коэффициента пуассона

Иллюстрации

Показать все

Реферат

Изобретение относится к области механических испытаний материалов и может быть использовано для определения коэффициента поперечной деформации (коэффициента Пуассона µ) как массивных материалов, так и отдельных фаз, структурных составляющих и покрытий.

Известен способ определения коэффициента Пуассона µ, заключающийся в изготовлении из испытуемого материала детали образца для испытаний на растяжение (сжатие) и последующего его испытания. В этом случае коэффициент Пуассона µ рассчитывают как отношение относительного поперечного сужения (расширения) к относительному продольному удлинению (сжатию) по ГОСТ 1497-84 - Методы испытаний на растяжение.

Указанный способ имеет следующие недостатки:

- высокую трудоемкость из-за необходимости изготовления и последующего испытания образца установленной формы;

- невозможность использовать способ при стопроцентном контроле деталей;

- невозможность использовать способ для деталей малых размеров;

- невозможность определять коэффициент Пуассона µ отдельных фаз, структурных составляющих и покрытий;

- низкую точность при испытании малопластичных материалов.

Наиболее близким по технической сущности является способ определения коэффициента Пуассона µ с использованием динамических методов испытания (см. Кузьменко В.А. Звуковые и ультразвуковые колебания при динамических испытаниях материалов. К.: Изд-во АН УССР. - 1963. - С.39-40) по формуле:

где Е - модуль Юнга (модуль упругости первого рода, или модуль нормальной упругости, или модуль упругости при растяжении);

G - модуль сдвига (модуль упругости второго рода).

Недостатками способа являются:

- необходимость предварительного определения как модуля упругости Е, так и модуля сдвига G;

- невозможность определения коэффициента Пуассона µ отдельных фаз, структурных составляющих и покрытий.

Сущность изобретения заключается в том, что по известному способу, по которому определяют модуль Юнга, с учетом которого рассчитывают коэффициент Пуассона, согласно изобретению испытуемый материал подвергают индентированию жестким индентором в виде правильной пирамиды при непрерывном вдавливании с построением диаграммы «нагрузка-перемещение индентора», по которой определяют характеристику пластичности δ_А как отношение площади между ветвями нагружения-разгружения к общей площади под кривой нагружения, определяют твердость по Мейеру НМ как отношение нагрузки к площади проекции отпечатка индентора на контактной поверхности, а величину коэффициента Пуассона µ рассчитывают по формуле:

где γ - угол между осью и боковой гранью пирамиды.

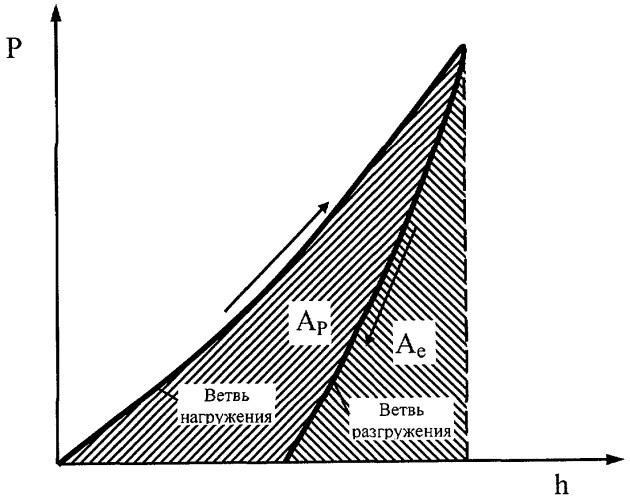
При выводе этой формулы исходили из равенства характеристики пластичности δ_А, определяемой по диаграмме «нагрузка-перемещение индентора» (см. чертеж), и характеристики пластичности δ_Н (δ_A=δ_H), определяемой при статических испытаниях на микротвердость (Yu.V.Milman, S.Dub, A.Golubenko. Plasticity characteristics obtained through instrumental indentation. Mater. Res. Soc. Symp. Proc. Vol.1049, 2008).

При этом:

(Yu.V.Milman, B.A.Galanov, S.I.Chugunova. Plasticity characteristic obtained through hardness measurement. Acta metall. mater., v.41, №9, 1993, p.2523-2532).

Отличительными признаками изобретения является то, что впервые для определения коэффициента Пуассона предложено использовать метод индентирования твердыми инденторами в виде правильной пирамиды, что позволяет определять коэффициент Пуассона отдельных фаз, структурных составляющих и покрытий.

Заявляемый способ реализуют следующим образом. Предварительно любым известным независимым способом находят модуль Юнга Е испытуемого материала. Затем в этом материале проводят непрерывное вдавливание жесткого индентора в виде правильной пирамиды с построением диаграммы в координатах «нагрузка-перемещение индентора» (см. чертеж). По диаграмме в соответствии с ISO 14577 и Yu.V.Milman. Plasticity characteristic obtained by indentation, J.Phys.D: Appl. Phys. 41 (2008) определяют величину характеристики пластичности δ_A как отношение площади между ветвями нагружения-разгружения А_р к общей площади под кривой нагружения (А=А_р+А_е) по формуле:

где А_р - площадь между ветвями нагружения-разгружения, характеризующая работу, затрачиваемую на пластическую деформацию;

А_е - площадь под ветвью разгружения, характеризующая работу, затрачиваемую на упругую деформацию.

После этого определяют площадь проекции отпечатка индентора на контактной поверхности, а твердость по Мейеру НМ рассчитывают по формуле:

где Р - усилие вдавливания в Н;

S - площадь проекции отпечатка на контактную поверхность.

Для точного и экспрессного определения площадей под ветвями нагружения-разгружения используют стандартные компьютерные программы.

Затем определяют коэффициент Пуассона µ по формуле (2).

Пример. Определение коэффициента Пуассона µ проводили на карбидных покрытиях NbC и TiC, на гальваническом хромовом покрытии, полученном электролитическим путем, а также на поликристаллических образцах титана и алюминия и на монокристалле кремния. Карбидные покрытия наносили на образцы, изготовленные из стали У8А, по способу, описанному в АС СССР №711782, БИ 1980, №3. Способ получения карбидных покрытий на поверхности металлов и сплавов / Лоскутов В.Ф., Хижняк В.Г., Бякова А.В. Хромовое покрытие наносили электролитическим методом по стандартной технологии на высокопрочный чугун.

Модуль упругости Е хрома, титана, ниобия, меди, а также карбидов титана и ниобия определяли на массивных образцах динамическим методом по собственной частоте колебаний (И.Н.Францевич, О.А.Чехова. Сб. Вопросы порошковой металлургии и прочности материалов. Изд. АН УССР, 6,36, 1958). Характеристику пластичности δ_A определяли по ISO 14577 при непрерывном вдавливании стандартного алмазного индентора Берковича с использованием прибора "Nano Indenter II" и построением диаграммы в координатах «нагрузка-перемещение индентора» по формуле (4). Расчет твердости по Мейеру НМ проводили по формуле (5). Полученные результаты представлены в таблице. В этой же таблице для сравнения приведены значения коэффициента Пуассона µ_c, взятые из справочной литературы для покрытий NbC, TiC и Cr (И.Н.Францевич, Ф.Ф.Воронов, С.А.Бакута. Упругие постоянные и модули упругости металлов и неметаллов. Киев: Наукова думка, 1982. - 286 с.), а также для поликристаллов Ti, Al и монокристалла Si, которые были рассчитаны в соответствии с прототипом.

Как видно из таблицы, погрешность при определении коэффициента Пуассона µ составляет не более 9%.

Таблица
Испытуемый материал	Предлагаемый способ	Справочные данные µС	Погрешность , %
Е, ГПа	δА	НМ, ГПа	µ
Покрытие NbC	420	0,52	28,40	0,213	0,220	3,2
Покрытие TiC	452	0,37	35,7	0,164	0,170	3,5
Покрытие Сr	202	0,69	11,7	0,298	0,310	3,9
Поликристалл Ti	120	0,89	2,85	0,329	0,360	8,6
Поликристалл Al	70	0,96	0,66	0,345	0,356	3,1
Монокристалл Si	169	0,50	11,9	0,213	0,223	4,5

Таким образом, предлагаемое решение позволяет расширить области использования способа за счет возможности проведения испытания малых по размеру объектов, например покрытий, отдельных фаз и структурных составляющих, снизить трудоемкость за счет исключения необходимости определения модуля сдвига G, повысить точность при испытании малопластичных материалов.

Результаты экспериментальной проверки свидетельствуют о пригодности способа для практического использования в исследовательских целях для оценки механических свойств изделий, а также в промышленном производстве.

Способ определения коэффициента Пуассона µ, включающий определения модуля Юнга Е, отличающийся тем, что испытуемый материал подвергают индентированию жестким индентором в виде правильной пирамиды при непрерывном вдавливании с построением диаграммы «нагрузка-перемещение индентора», по которой определяют характеристику пластичности δ_А, как отношение площади между ветвями нагружения-разгружения к общей площади под кривой нагружения, определяют твердость по Мейеру НМ, как отношение нагрузки к площади проекции отпечатка индентора на контактной поверхности, а величину коэффициента Пуассона µ, рассчитывают по формуле ,где γ - угол между осью и боковой гранью пирамиды.