Способ получения функции распределения вероятностей исходного сигнала системы

Способ получения функции распределения вероятностей исходного сигнала системы

Иллюстрации

Показать все

Реферат

Изобретение относится к сфере измерительной техники. Изобретение может быть использовано для получения точно заданных вероятностных характеристик исходного сигнала.

Задача изобретения - получение функции распределения вероятности (ФРВ) сигнала на выходе системы.

Поставленная задача достигается тем, что определяется возможность нахождения аналитически функции, обратной к y(x) (функции, описывающей систему), и производится функциональное преобразование по заданному алгоритму.

Изобретение состоит в том, что способ получения ФРВ заключается в в осуществлении функционального преобразования y(x) по алгоритму:

int{S_x(x(y))dx/dy}/{int_[a, b](S_x(x(y))dx/dy)dy},

где int - неопределенный интеграл функции, int_[a,b] - интеграл Лебега по области значений на промежутке x∈[a, b], S_x - плотность распределения испытательного сигнала.

Получить ФРВ аналитически для заданной функции y(x) возможно, если ФРВ случайной величины x на промежутке [a, b] известна и можно найти аналитически обратную функцию x(y). Пусть x - случайная величина с заданной функцией распределения.

Пусть исходная случайная величина ξ имеет плотность распределения S_x(x) на отрезке [a, b]. Пусть функция, через которую проходит сигнал, определена как y(x). Если обратная функция x(y) на промежутке [а, b] однозначна, непрерывна и dy/dx не обращается в ноль, тогда плотность распределения результирующей случайной величины S_y(y) пропорциональна:

Используя нормировку, находим абсолютное значение S_y:

где int_[a, b] - это интеграл Лебега по области значений y на x∈[a, b] (Не обязательно, чтобы интервал совпадал c [y(а), у(b)], поскольку y(x) может иметь разрыв. Например, y=x^-1 имеет разрыв на [-1, 1].) Результат (2) - функция плотности вероятности (ПВ). Первая производная от ФРВ это ПВ. Если x(y) неоднозначно определена и(или) dy/dx обращается в ноль на [а, b], мы используем другой метод. Также для тех y, которые не являются значениями x(y) в точках dy/dx=0, используется следующий метод:

пусть y₀ - точка, в которой нужно найти S_y.

1. Получим множество отрезков [a₁, b₁], [a₂, b₂], …, [a_n, b_n], … на каждом из которых y(x) монотонна и неразрывна, dy/dx не имеет нулей, и существует только одно решение для уравнения y(x_n)=y₀. В худшем случае количество таких интервалов счетно.

2. Возьмем отрезок [a_n, b_n], найдем вероятность P_n, что ξ принадлежит этому фрагменту (это , где - определенный интеграл от a_n до b_n), получим частную плотность:

где - определенный интеграл от y(a_n) до y(b_n).

3. Общая плотность - это сумма частных плотностей

где sum_n - сумма элементов по n.

4. Значение интеграла (3) и плотность вероятности S_yn(y₀) значимо положительные величины.

5. Результат (4) - это ПВ, для получения ФРВ необходимо его проинтегрировать.

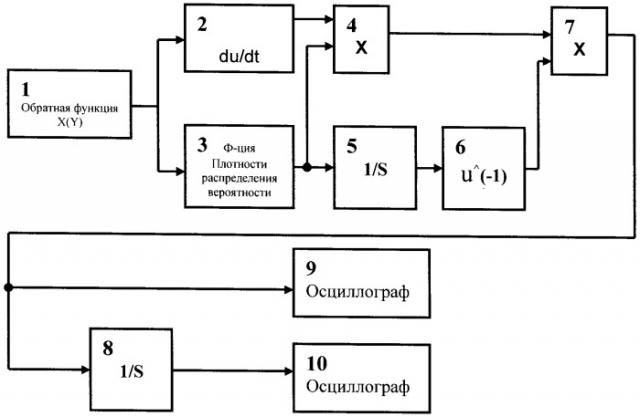
Данный способ может быть реализован в простых технических блоках. Схема реализации представлена на чертеже, где

- блок 1 - блок генерирования сигнала x(y), соответствующего обратной функции к испытательному сигналу y(x);

- блок 2 - блок дифференцирования;

- блок 3 - блок функции плотности распределения испытательного сигнала;

- блоки 4 и 7 - блоки перемножения сигналов;

- блоки 5 и 8 - блоки-интеграторы;

- блок 6 - блок возведения в степень (-1);

- блоки 9 и 10 - осциллографы.

Выход блока 1 соединен со входом блока 2 и входом блока 3. Выход блока 2 соединен со входом блока 4. Выход блока 3 соединен со входом блока 4 и входом блока 5. Выход блока 4 соединен со входом блока 7. Выход блока 5 соединен со входом блока 6. Выход блока 6 соединен со входом блока 7. Выход блока 7 соединен со входом блока 8 и входом блока 9. Выход блока 8 соединен со входом блока 10. Передача сигнала происходит в направлении от выхода ко входу.

Система функционирует следующим образом. Сигнал с выхода блока генерирования сигнала 1 поступает на вход блока 2, где дифференцируется, и вход блока 3, где преобразуется согласно функции плотности распределения испытательного сигнала, сигнал с выхода блока 2 поступает на вход умножителя 4, где перемножается с сигналом с выхода блока 3, сигнал с выхода блока 3 также поступает на вход блока интегрирования 5, где интегрируется, сигнал с выхода блока 5 поступает на вход блока 6 возведения в степень -1, сигналы с выходов блока 6 и 4 поступают на вход блока 7, где перемножаются. Сигнал с выхода блока 7 поступает на вход блока 8, где интегрируется, и на вход блока 9, где наглядно отображается на осциллографе, сигнал с выхода блока 8 также поступает на вход блока осциллографа 10, где отображается наглядно.

Технический результат использования изобретения заключается в получении точных вероятностных характеристик исходного сигнала, что может применяться, например, для создания эталона исходного сигнала в системах тестирования технических устройств.

Способ получения функции распределения вероятностей исходного сигнала с заданной плотностью распределения испытательного сигнала на промежутке, заключающийся в пропускании сигнала описываемого функцией обратной к функции распределения вероятностей входного сигнала через дифференциатор, и, параллельно через блок, преобразующий входящий сигнал случайно, с заданной плотностью распределения вероятности, затем сигнал на выходе данного блока поступает на первый из двух блоков умножения, где перемножается с выходным сигналом дифференциатора, и на первый из двух интеграторов; сигнал, выходящий с интегратора, поступает на блок возведения в степень -1, с выхода которого сигнал поступает на второй из двух умножителей, где перемножается с выходным сигналом с первого умножителя, а выходной сигнал со второго умножителя пропускается через второй из двух интеграторов, на выходе которого получается функция распределения вероятностей исходного сигнала, что можно представить в виде алгоритма:int{Sx(x(y))dx/dy}/{int_[a,b](Sx(x(y))dx/dy)dy},где int - неопределенный интеграл функции, int_[a,b] - интеграл Лебега по области значений у на промежутке х∈[a,b}, Sx - плотность распределения испытательного сигнала.