Способ анализа спектров люминесценции

Способ анализа спектров люминесценции

Иллюстрации

Показать все

Реферат

Заявляемое изобретение относится к способам автоматизированного анализа результатов экспериментальных измерений, в частности к способам автоматизированного анализа результатов люминесцентных измерений, таких как спектры оптической люминесценции, спектры радиолюминесценции (в том числе импульсной катодолюминесценции, рентгенолюминесценции и ионолюминесценции), разного рода поляризованные спектры люминесценции, спектры и кривые термостимулированной люминесценции, спектры оптического поглощения, спектры оптического отражения, с использованием методов математического моделирования.

Одним из направлений автоматизированного анализа результатов экспериментальных измерений вообще и люминесцентных спектров в частности является математическое моделирование, в рамках которого используются те или иные модели измерительных процессов, характеризующиеся определенным набором параметров. Задача процедуры моделирования сводится к такому подбору параметров модели, при котором будет наблюдаться наилучшее с точки зрения заданного критерия совпадения результатов расчета и результатов эксперимента. Таким образом, ключевым моментом всех способов анализа результатов экспериментальных измерений является тот или иной критерий соответствия расчета эксперименту, от надежности и корректности которого будет зависеть точность и обоснованность результатов анализа с использованием методов математического моделирования.

Известен способ анализа спектров люминесценции, заключающийся в субъективном определении человеком компонентов сложного спектра люминесценции путем приблизительной оценки позиции колоколообразных составляющих. Этот способ используется во множестве научных и практических работ, например в работе: Люминесценция объемных, волоконных и наноразмерных кристаллов LiF и NaF / А.Н.Черепанов, В.Ю.Иванов, Т.С.Королева, Б.В.Шульгин. Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2006. 304 с. Среди несомненных плюсов этого способа - предельная простота. Однако, за счет того что определение компонент происходит «на глаз», без четких моделей люминесцентного процесса и явных критериев соответствия, данный способ не имеет определенной точности, ненадежен, субъективен, т.е. является оценочным, и не может потому рассматриваться как способ точного анализа люминесцентных спектров. Кроме того, известный метод требует постоянного участия человека и не относится к автоматизированным способам анализа.

Наиболее близким к заявляемому является способ анализа спектров люминесценции, основанный на разложении спектров люминесценции на гауссианы, путем подбора таких параметров гауссианов, при которых сумма квадратов разностей расчетных и экспериментальных значений по всем экспериментальным точкам имеет минимальное значение. Этот способ используется во множестве научных и практических работ, например в работе: Luminescence spectroscopy of NaF:U bulk and fiber crystals / B.V.Shulgin, A.N.Tcherepanov, V.Yu. Ivanov, T.S.Koroleva, M.M.Kidibaev, Ch. Pedrini, Ch. Dujardin // Journal of Luminescence. 2007. Vol.125, Iss. 1-2. P.259-265. Минимизация суммы квадратов разностей расчетных и экспериментальных значений широко применяется в математике при сопоставлении различных кривых, и основными достоинствами такого подхода являются простота и независимость от природы сопоставляемых зависимостей. Последнее, однако, является и недостатком известного способа. В ряде случаев одинаковое по абсолютным значениям расстояние между кривыми не означает одинаковую близость физических процессов, описываемых этими кривыми. Подобный эффект имеет место, в частности, при измерении величин, принимающих целочисленные значения или значения, пропорциональные таковым. Действительно, если измеренная целочисленная величина имеет значение N, то погрешность ее равна . Поэтому, если на экспериментальной кривой одновременно встречаются целочисленные значения, заметно отличающиеся по величине, то и близость моделированной кривой к этим экспериментальным значениям должна быть различной: к экспериментальным точкам с малыми значениями N моделированная кривая должна быть существенно ближе, чем к экспериментальным точкам с большими значениями N. В известном способе анализа (сумма квадратов разностей расчетных и экспериментальных значений) предполагается, что моделированная кривая проходит в одинаковой близости как от больших, так и от малых значений N, т.е. известный способ безразличен к значению N: он не учитывает погрешность определения целочисленных величин или величин, пропорциональных таковым. При измерении спектров люминесценции каждая экспериментальная точка, будучи пропорциональной целочисленному количеству зарегистрированных фотонов, имеет свою, как правило, отличную от других точек спектра, погрешность. По этой причине известный способ анализа люминесцентных спектров является неоптимальным для анализа спектров люминесценции, поскольку не учитывает индивидуальную погрешность каждой экспериментальной точки.

Задача предлагаемого изобретения заключается в разработке такого способа анализа спектров люминесценции, в котором корректно учитывается погрешность измерения каждой точки спектра. Задача решается за счет подбора необходимого критерия соответствия результатов расчета и эксперимента.

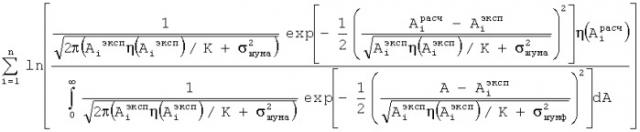
Суть предлагаемого способа анализа люминесцентных спектров заключается в разложении спектров люминесценции на гауссианы путем подбора таких параметров гауссианов, при которых выражение

где - значение амплитуды i-й экспериментальной точки в спектре люминесценции; - значение расчетной амплитуды спектра люминесценции в точке с той же энергией или длиной волны, что и у i-й экспериментальной точки; К - коэффициент пропорциональности между амплитудой сигнала и количеством зарегистрированных фотонов; η - функция Хэвисайда; σ_шума - стандартное отклонение погрешности измерения амплитуды сигнала, связанное с шумами аппаратуры,

принимает максимально возможное значение.

Предлагаемый способ анализа люминесцентных спектров основан на следующем. С методической точки зрения измерение спектров люминесценции заключается в определении количества фотонов, испускаемых исследуемым образцом. Амплитуда сигнала (W) на выходе измерительной аппаратуры считается пропорциональной количеству зарегистрированных фотонов:

где N(W) - количество зарегистрированных фотонов; К- коэффициент пропорциональности между амплитудой сигнала и количеством зарегистрированных фотонов (зависит от особенностей построения измерительного тракта, его коэффициента усиления, включает в себя также эффективность регистрации фотонов с помощью ФЭУ).

Поскольку амплитуда сигнала A^эксп(W) на выходе измерительной аппаратуры пропорциональна целочисленной величине N(W), то погрешность измерения A^эксп(W) должна быть пропорциональна . Распределение во времени сигналов, соответствующих регистрируемым фотонам на выходе измерительного тракта, подчиняется распределению Пуассона, которое при количестве отсчетов N>30 переходит в нормальное распределение.

Очевидно, что стандартное отклонение такого распределения имеет значение:

В связи с тем что в экспериментах по измерению спектров люминесценции количество регистрируемых фотонов в единицу времени, как правило, заметно превосходит 30, погрешность измерения амплитуды сигнала может быть описана в первом приближении следующим нормированным нормальным распределением:

На самом деле погрешность определения амплитуды сигнала зависит не только от амплитуды самого сигнала, но и от шумовых характеристик измерительного тракта. Если считать, что амплитудное распределение шума носит характер нормального распределения со стандартным отклонением σ_шума, то суммарное стандартное отклонение равно:

Шумы аппаратуры, будучи распределенными вокруг нуля, могут формировать как положительные, так и отрицательные (не имеющие физического смысла при пересчете в число фотонов) сигналы. По этой причине, если экспериментальная точка имеет отрицательную амплитуду, то погрешность амплитуды такой точки определяется только шумовой составляющей, т.е. число фотонов, сформировавших такой отсчет, равно нулю (N=0). Математически данное предположение может быть записано с использованием функции Хэвисайда η(x), которая равна нулю при x<0 и равна единице при х≥0:

Тогда вероятность соответствия некоторого значения амплитуды А значению амплитуды A^эксп может быть представлена формулой:

Однако, если величина А - это расчетное (моделированное) значение A^расч, она не может быть отрицательной по физическому смыслу. По этой причине в выражение (5) необходимо ввести дополнительный множитель в виде функции Хэвисайда, который будет приравнивать к нулю вероятность соответствия значения амплитуды А^расч значению A^эксп в случае отрицательных значений величины A^расч. Введение дополнительного множителя приводит к необходимости перенормировки функции p(A^расч; A^эксп], поскольку он отсекает значения с А<0:

Поскольку экспериментальный спектр представляет из себя набор пар значений , то для его сравнения с моделированным спектром последний должен быть представлен в виде аналогичного набора данных, т.е. в виде пар значений Значение получается из выражения (2) путем подстановки соответствующего значения энергии: . Таким образом, формируются ряды данных которые и подлежат сравнению между собой.

Соответствие моделированной и экспериментальной кривых определяется как одновременное соответствие расчета и эксперимента в каждой точке W_i (в точке W₁, и в точке W₂, и в точке W₃ и так далее до точки W_n), т.е. как произведение вероятностей соответствия в каждой отдельной точке:

где n - количество экспериментальных точек. Чем больше соответствие между моделированной и экспериментальной кривыми, тем большее значение приобретает показатель Р. Однако применение для вычисления показателя Р формулы типа (7), т.е. формулы, содержащей произведение n членов, неудобно на практике. По этой причине произведение n членов заменяется на сумму следующим образом:

а требование Р→max рассматривается как требование:

Таким образом, суть предлагаемого способа анализа сводится к подбору таких параметров моделируемого спектра, при которых выполняется выражение (9). Подбор выполняется стандартными методами многопараметрической оптимизации, например методом Ньютона.

Дополнительным преимуществом предлагаемого способа анализа люминесцентных спектров является возможность его применения для ряда других видов измерений, заключающихся в регистрации целочисленных величин или величин, пропорциональных таковым, например, при анализе кинетик затухания люминесценции.

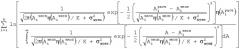
Способ анализа спектров люминесценции, основанный на разложении спектров люминесценции на гауссианы, путем подбора таких параметров гауссианов, при которых сумма квадратов разностей расчетных и экспериментальных значений по всем экспериментальным точкам имеет минимальное значение, отличающийся тем, что подбор параметров гауссианов ведется таким образом, что выражение где - значение амплитуды i-й экспериментальной точки в спектре люминесценции; - значение расчетной амплитуды спектра люминесценции в точке, с той же энергией или длиной волны, что и у i-й экспериментальной точки; К - коэффициент пропорциональности между амплитудой сигнала и количеством зарегистрированных фотонов; η - функция Хэвисайда; σ_шума - стандартное отклонение погрешности измерения амплитуды сигнала, связанное шумами аппаратуры, принимает максимально возможное значение.