Способ обработки сейсмических данных с использованием дискретного вейвлет-преобразования

Способ обработки сейсмических данных с использованием дискретного вейвлет-преобразования

Иллюстрации

Показать все

Реферат

Изобретение относится к области сейсмической разведки, в частности к способам обработки сейсмических данных.

Известен способ обработки сейсмических данных, позволяющий получить улучшения количественной оценки и визуализации отражения от тонкого пласта, а также от боковых нарушений сплошности горной породы, основанный на выявлении специальных эффектов в амплитудных спектрах участков сейсмических трасс, от исследуемых геологических объектов (патент РФ №2187828, G01V 1/30). Способ реализуется с использованием преобразования Фурье. Авторами этого способа показано, что отражение от тонкого пласта имеет характерную форму выражения в частотной области. Его амплитудно-частотный спектр содержит периодическую последовательность отметок (всплесков), отстоящих друг от друга на расстояние, обратно пропорциональном «временной толщине» тонкого пласта.

Известно использование дискретного вейвлет-преобразования для обработки и анализа сигналов разнообразной природы (патент РФ №2246132, G06F 17/14, прототип). В указанном патенте дано подробное описание способа и устройства быстрого вычисления вейвлет-преобразований, которое может быть использовано при обработке сигналов, в частности в области обработки экспериментальных данных в физике, в гидроакустике, сейсмоакустике, радиолокации и т.д. В данном известном техническом решении посредством быстрого вычисления вейвлет-преобразования дается возможность анализировать сигнал с произвольной точностью измерения масштабов и временных сдвигов избыточного дискретного вейвлет-преобразования сигнала с произвольно заданным (выбранным) малым шагом дискретизации масштабных коэффициентов.

В настоящее время наибольшее распространение при обработке и интерпретации сейсмических данных получили спектральные способы обработки с использованием быстрого преобразования Фурье, например, как это показано выше. Однако, как показала практика, обработка с использованием быстрого преобразования Фурье различного рода сейсмических данных не всегда является исчерпывающей и достаточно эффективной, поэтому проблема анализа сейсмических данных в различных масштабах (координатах n-мерного пространства) остается одной из актуальных в современном процессе их обработки.

Задачей настоящего изобретения является расширение возможностей и арсенала способов обработки сейсмических данных, обеспечивающих повышение эффективности, информативности и достоверности результатов обработки сейсмических данных при геолого-геофизических исследованиях земной коры, в том числе в области поиска углеводородсодержащих объектов сложной структуры.

Технический результат изобретения - обеспечение возможности анализа сейсмических данных с локализацией особенностей сигнала в вейвлет-частотной области с повышенным качеством выделения особенностей сигнальной составляющей в пространственно-временных координатах, с разделением волновых полей на отдельные составляющие и повышением отношения сигнал/помеха.

Поставленная задача решается за счет того, что в способе обработки сейсмических данных с использованием дискретного вейвлет-преобразования, включающем представление сейсмических данных в виде набора сейсмических трасс, согласно изобретению каждую из исходных сейсмических трасс, представленную в виде вектора отсчетов, подвергают дискретному вейвлет-преобразованию (М итераций) с получением вектора вейвлет-коэффициентов, содержащего детализирующие вейвлет-коэффициенты Кn с первого по уровень М включительно, а также гладкие вейвлет-коэффициенты последнего уровня преобразования O_M, далее вектор вейвлет-коэффициентов разделяют на ряд векторов, каждый из которых содержит детализирующие вейвлет-коэффициенты K_n одного уровня и нули на месте всех остальных вейвлет-коэффициентов (детализирующий вектор уровня n), а также вектор, содержащий гладкие вейвлет-коэффициенты O_M и нули на месте всех детализирующих коэффициентов (детализирующий вектор уровня М+1), каждый из указанных детализирующих векторов уровней с 1 по М+1, подвергают процедуре обратного дискретного вейвлет-преобразования с получением М+1 слоев детализации dl(n) и представлением (визуализацией) исходного сейсмического сигнала в виде составляющих dl(n) с различными энергетическими и частотными характеристиками; каждый из указанных составляющих (слоев детализации dl(n)) анализируют по их целевой значимости с учетом решаемой сейсмической задачи, после чего осуществляют выборку значимых отдельных слоев детализации вейвлет-разложения исходного сейсмического сигнала с построением их частичных сумм для последующей обработки и интерпретации сейсмических данных.

Способ согласно изобретению основан на следующем.

Известно, что все способы подавления волновых помех, как правило, построены с учетом выделенных аномальных значений их характеристик относительно параметров полезного сигнала. Как показано авторами, для обработки и анализа нестационарных сигналов, к которым относятся волновые сейсмические поля, может быть успешно применено дискретное вейвлет-преобразование, которое позволило эффективно выделять аномальные характеристики наблюдаемых сейсмических полей.

В основе алгоритма быстрого дискретного вейвлет-преобразования лежит использование двух связанных между собой цифровых фильтров, один из которых является сглаживающим, а второй - детализирующим, настроенным на особенности сигнала. Широкий набор существующих базовых функций вейвлетов позволил адаптировать их к обработке сейсмических данных, обеспечивающей повышение отношения сигнал/помеха.

Последовательное применение нескольких итераций вейвлет-преобразований по пирамидальному алгоритму Малла (Mallat) (входными данными для каждого последующего уровня преобразования является гладкая часть сигнала, полученная при преобразовании предыдущего уровня) позволяет получить вейвлет-разложение сигнала.

Совокупность детализирующих коэффициентов, полученных в результате n-ной итерации вейвлет-преобразования, будем в дальнейшем называть коэффициентами n-го уровня детализации. При этом на каждой итерации количество как детализирующих, так и гладких коэффициентов уменьшается вдвое относительно числа коэффициентов входного сигнала. На любом этапе преобразованный сигнал содержит то же число отсчетов, что и исходный сигнал, этого достаточно для выполнения взаимно однозначного обратного вейвлет-преобразования.

Разработанный авторами способ обработки сейсмических данных с применением дискретного вейвлет-разложения обеспечивает восстановление сигнала из его вейвлет-разложения по разным слоям детализации. Слой детализации вейвлет-разложения уровня n - это сигнал, полученный восстановлением посредством обратного дискретного вейвлет-преобразования только из коэффициентов n-го уровня детализации, приняв все остальные коэффициенты (и детализирующие, и гладкие) других уровней равными нулю.

Все проводимые операции, а именно прямое дискретное вейвлет-преобразование, разложение вектора вейвлет-коэффициентов на сумму векторов, обратное дискретное вейвлет-преобразование являются линейными. Вследствие этого, в результате проведенных операций исходный вектор данных однозначно раскладывается на ряд слоев детализации вейвлет-разложения, полная сумма которых однозначно восстанавливает исходный вектор данных S.

Сложное волновое поле раскладывается на составляющие, различающиеся энергетическими и частотными характеристиками. При этом первый слой детализации вейвлет-разложения содержит наиболее высокочастотные особенности, а последующие слои детализации - более гладкие (низкочастотные) составляющие исходного сигнала. В дальнейшем полученные слои детализации вейвлет-разложения разных уровней могут быть использованы как по отдельности, так и в составе частичных сумм при обработке и анализе сейсмических данных.

Как правило, процедура вейвлет-разложения сейсмических записей выполняется потрассно с использованием дискретных вейвлетов с высокой гладкостью.

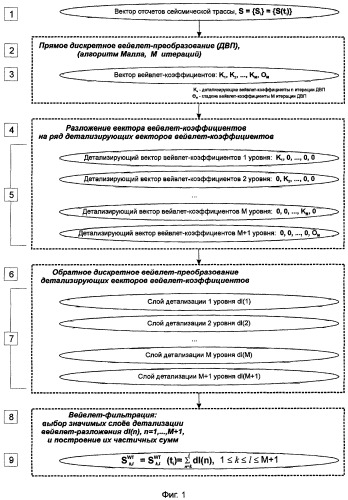
На фиг.1 показана блок-схема последовательности операций при осуществлении способа согласно изобретению. Фиг.2-5 иллюстрируют реализацию способа согласно изобретению.

Способ согласно изобретению осуществляют в следующей последовательности операций.

Исходная сейсмическая трасса, состоящая из дискретных отсчетов, рассматривается как вектор входных данных S (поз.1, фиг.1) для прямого дискретного вейвлет-преобразования (поз.2, фиг.1). На первой итерации дискретного вейвлет-преобразования (вектор входных данных умножается на матрицу вейвлет-преобразования) вектор данных преобразовывается в вектор вейвлет-коэффициентов. Гладкие коэффициенты участвуют в дальнейшем преобразовании, детализирующие коэффициенты сохраняются на всех уровнях вейвлет-разложения. Как было сказано выше, для вейвлет-разложения по пирамидальному алгоритму Малла в каждой последующей итерации дискретного вейвлет-преобразования в качестве вектора входных данных используется вектор гладких коэффициентов, полученный на предыдущей итерации дискретного вейвлет-преобразования.

Как показано на поз.3, фиг.1, после проведения М итераций прямого дискретного вейвлет-преобразования вектор выходных данных содержит коэффициенты вейвлет-разложения: детализирующие коэффициенты K_n вейвлет-преобразования от первого по уровень М включительно, а также гладкие коэффициенты O_M последней итерации уровня М.

Из вектора вейвлет-коэффициентов с использованием обратного дискретного вейвлет-преобразования (М итераций) можно однозначно восстановить вектор исходных данных. Предлагается проводить восстановление исходного сейсмического сигнала во временную область из вектора вейвлет-коэффициентов последовательно «по частям». Сначала вектор преобразованных данных разделяется на ряд М+1 детализирующих векторов (поз.4, поз.5. фиг.1). Результатом разделения являются векторы: первый вектор содержит коэффициенты первого уровня детализации и нули на месте всех остальных коэффициентов; второй вектор содержит коэффициенты второго уровня детализации и нули на месте всех остальных коэффициентов; вектор М содержит коэффициенты детализации уровня М и нули на месте всех остальных коэффициентов; вектор (М+1) содержит гладкие коэффициенты последнего уровня М вейвлет-преобразования и нули на месте всех детализирующих коэффициентов всех уровней (поз.5, фиг.1).

Далее каждый из указанных детализирующих векторов, содержащий только часть коэффициентов из общего вектора преобразованных данных, подвергают обратному дискретному вейвлет-преобразованию (поз.6, фиг.1). Результат этой операции для n-го детализирующего вектора авторы называют слоем детализации уровня n (поз.7, фиг.1).

Первый слой детализации содержит наиболее высокочастотные составляющие исходного сигнала, каждый последующий слой детализации содержит все более и более гладкие составляющие. Так как сейсмические волны разных типов имеют разные частотные и энергетические характеристики, то при таком разложении отдельные составляющие сейсмического сигнала представляются в различных слоях детализации.

При необходимости выделения и анализа сейсмической волны конкретного типа учитывают только те слои детализации dl(k), …, dl(l), в которых эти волны значимо представлены (например, по интенсивности), а в последующем используют также сумму этих слоев детализации (вейвлет-фильтрация) (поз.8, поз.9 фиг.1).

Способ согласно изобретению, как он описан выше, расширяет возможности обработки сейсмических данных за счет разложения исходного сигнала на ряд слоев детализации, обладающих разными энергетическими и пространственно-временными характеристиками, и возможности анализировать их по отдельности, а также в составе частичных сумм, включающих только выбранные «полезные» слои детализации.

Ниже приведен пример реализации способа согласно изобретению.

Возможности вейвлет-фильтрации с использованием вейвлет-разложения по различным слоям детализации для выделения и подавления регулярных волн-помех были апробированы на полевых сейсмических данных. Для анализа и обработки были использованы данные (волновые зонды), полученные ОАО «Енисейгеофизика» на Оморинской площади (Сибирская платформа) с использованием трехкомпонентных цифровых акселерометров DSU3 (Sercel, Франция). Система наблюдений центральная, максимальная дистанция составила ±3440 м. Длина расстановки сейсмодатчиков составила 860 м, шаг между пунктами приема 5 м, группирование сейсмодатчиков не применялось. Выполнено 8 взрывных возбуждений.

Особенностью сейсмогеологического разреза данного района исследований является высокая скорость сейсмических волн, а также наличие в верхней части разреза сейсмической азимутальной анизотропии с латеральными изменениями. Наблюдаемое на трех компонентах (Zz, Zx, Zy) поле сейсмических волн имеет сложную интерференционную структуру: прослеживаются волны разной поляризации (продольные, поперечные и обменные). В области прослеживания целевых отраженных продольных волн (0,7-1,4 с) на всех волновых зондах регистрируются интенсивные низкочастотные поверхностные волны (волновые помехи).

Вейвлет-разложение сейсмических зондов в соответствии со способом согласно изобретению выполнено с базовым вейвлетом высокой гладкости Coiflet 30. На фиг.2 показан фрагмент обработки исходного сигнала (Z-компонента) на этапе процедуры обратного дискретного вейвлет-преобразования (операция поз.6, фиг.1) с получением слоев детализации dl(n). Как и ожидалось, крайние слои детализации вейвлет-разложения вертикальной компоненты (Zz) сейсмического зонда, уровни dl(1), dl(2), dl(7), являются наиболее энергетически слабыми. Первый слой детализации dl(1) содержит в основном высокочастотный, случайный шум. Поле низкочастотных поверхностных волн (регулярный шум) сосредоточено в слоях детализации dl(6) и dl(7). Целевые отраженные продольные РР и обменные SP, PS сейсмические волны наиболее уверенно прослеживаются на средних слоях детализации dl(3), dl(4) и dl(5).

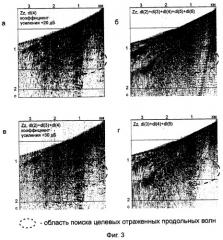
Далее на фиг.3 приведены результаты вейвлет-фильтрации: варианты частичных сумм, построенных из разных слоев детализации dl(n). На фиг.3а показан отдельный выделенный слой детализации dl(4) с увеличенным коэффициентом усиления, пунктиром выделена область поиска целевых отраженных продольных волн. Также приведены частичные суммы слоев детализации (поз.8, фиг.1) со второго по шестой уровни (фиг.3б), со второго по четвертый уровни (фиг.3в) и с третьего по пятый уровни (фиг.3г).

Как видно на фиг.3в, вейвлет-фильтрация с использованием суммы слоев детализации dl(2)+dl(3)+dl(4) значительно (более чем в 10 раз) снизила интенсивность случайного шума и регулярных волн-помех, в результате чего в целевом интервале прослеживания продольных отраженных волн повысилось отношение сигнал/помеха в несколько раз.

На фиг.4 показан пример, демонстрирующий применение способа согласно изобретению, для подавления регулярных поверхностных волн-помех, в сравнении с применением частотной фильтрации (преобразование Фурье). На фиг.4а приведена исходная сейсмическая запись, черным квадратом выделен фрагмент, который будет показан более детально в дальнейшем, пунктиром внутри квадрата показана область выделения целевой отраженной продольной волны. На фиг.4б приведен указанный фрагмент исходной сейсмической записи перед обработкой. На фиг.4в приведен тот же указанный фрагмент после применения вейвлет-фильтрации (частичная сумма слоев детализации второго, третьего и четвертого четвертый уровней). На фиг.4г приведен тот же указанный фрагмент после применения полосовой частотной фильтрации 20-80 Гц. Как видно из сравнения фрагментов 4в и 4г, при применении вейвлет-фильтрации подавлены низкочастотные поверхностные волны-помехи в большей степени, при этом сохранены высокочастотные составляющие отраженных продольных волн, разрешенность сейсмической записи выше.

На фиг.5 показан пример применения вейвлет-фильтрации для подавления случайных помех и повышения отношения сигнал/помеха в области первых вступлений. На фиг.5а приведен фрагмент исходной сейсмической записи, полученной при глубинных исследованиях методом ГСЗ при системе наблюдений «суша-море», возбуждение - морские пневмоизлучатели СИН-6М, регистрация - наземная, автономная станция РОСА-А. На фиг.5б приведен тот же фрагмент после применения вейвлет-фильтрации (частичная сумма третьего и четвертого слоев детализации). На фиг.5в приведен тот же фрагмент после применения полосовой частотной фильтрации 6-36 Гц. Как видно из сравнения фрагментов 5б и 5в, применение вейвлет-фильтрации снижает случайный шум и повышает соотношение сигнал/помеха в большей степени, чем полосовая частотная фильтрация, при этом прослеживается более высокая разрешенность сейсмической записи.

Приведенные примеры убедительно демонстрируют, что способ обработки сейсмических данных с использованием вейвлет-фильтрации, согласно изобретению, позволяет эффективно подавлять низкочастотные волны-помехи в сейсмическом поле, сохраняя структуру сигнальной составляющей практически неизменной и обеспечивает, таким образом, более достоверное (по сравнению с частотной фильтрацией) выделение целевых волн, имеющих высокую информативную и прогнозную значимость при глубинных сейсмических исследованиях.

Кроме того, очевидно, что анализ сейсмических данных с использованием вейвлет-фильтрации, согласно изобретению, по слоям детализации расширяет возможности обработки и интерпретации волновых полей.

Способ обработки сейсмических данных с использованием дискретного вейвлет-преобразования, включающий представление сейсмических данных в виде набора сейсмических трасс, отличающийся тем, что каждую из исходных сейсмических трасс, представленную в виде вектора отсчетов, подвергают дискретному вейвлет-преобразованию (М итераций) с получением вектора вейвлет-коэффициентов, содержащего детализирующие вейвлет-коэффициенты К_n с первого по уровень М включительно, а также гладкие вейвлет-коэффициенты последнего уровня преобразования Ом, далее вектор вейвлет-коэффициентов разделяют на ряд векторов, каждый из которых содержит детализирующие вейвлет-коэффициенты К_n одного уровня и нули на месте всех остальных вейвлет-коэффициентов (детализирующий вектор уровня n), а также вектор, содержащий гладкие вейвлет-коэффициенты О_M и нули на месте всех детализирующих коэффициентов (детализирующий вектор уровня М+1), каждый из указанных детализирующих векторов уровней с 1 по М+1 подвергают процедуре обратного дискретного вейвлет-преобразования с получением М+1 слоев детализации dl(n) и представлением (визуализацией) исходного сейсмического сигнала в виде составляющих dl(n) с различными энергетическими и частотными характеристиками; каждую из указанных составляющих (слоев детализации dl(n)) анализируют по целевой значимости с учетом решаемой сейсмической задачи, после чего осуществляют выборку значимых отдельных слоев детализации вейвлет-разложения исходного сейсмического сигнала для построения их частичных сумм для последующей обработки и интерпретации сейсмических данных.