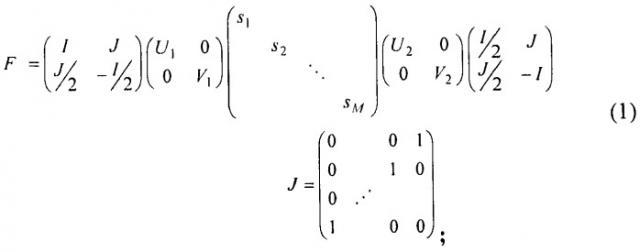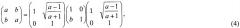Обратимая двумерная предварительная и постфильтрация для перекрывающегося биортогонального преобразования

Обратимая двумерная предварительная и постфильтрация для перекрывающегося биортогонального преобразования

Иллюстрации

Показать все

Реферат

Информация о связанной заявке

Эта заявка является частичным продолжением патентной заявки США № 11/015148 на имя Tu et al., озаглавленной "Reversible Overlap Operator For Efficient Lossless Data Compression", от 17 декабря 2004 года, включенной в данный документ посредством ссылки.

Область техники

Изобретение относится, в общем, к сжатию цифрового мультимедийного сигнала (например, видео и изображения) с использованием перекрывающегося преобразования.

Уровень техники

Перекрывающиеся преобразования

Перекрывающееся преобразование является эффективным методом обработки сигналов, который используется при сжатии данных. См., например, H.S. Malvar, "Signal Processing with Lapped Transforms", Boston, MA: Artech House, 1992 г. Однако до настоящего времени эффективные перекрывающиеся преобразования с линейной фазой не были сформулированы и не применялись для сжатия (обратимого) данных без потерь.

Как описано более подробно ниже, известно, что перекрывающееся преобразование может быть сформулировано как предварительная фильтрация, за которой следует преобразование данных (и его инверсия как обратное преобразование данных, за которым следует постфильтрация). См., например, H.S. Malvar, "A pre- and post-filtering technique for the reduction of blocking effects", Proc. Picture Coding Symposium, Стокгольм, Швеция, июнь 1987 г.; и T.D. Tran, J. Liang, C. Tu, "Lapped Transform via Time-Domain Pre- and Post-Filtering", IEEE Trans. on Signal Processing, том 51, номер 6, июнь 2003 г. Преобразование данных без потерь может быть использовано в данной формулировке для достижения хорошей степени обратимости. До настоящего времени считалось, что только определенное ограниченное множество предварительных и постфильтров может быть выбрано для обеспечения обратимости. Этот ограниченный набор имеет существенные ограничения по производительности сжатия (скорость в зависимости от искажения - R-D). В работе W. Dai, T. Tran, "Regularity-constrained pre- and post-filtering for block DCT-based systems", IEEE Trans. on Signal Processing, том 51, стр. 2568-2581, октябрь 2003 г., представлена структура, в которой большинство элементов являются обратимыми и которая имеет хорошие свойства сжатия.

В сжатии аудиосигналов был введен ряд структур для обратимых перекрывающихся преобразований (см., например, R. Geiger, J. Herre, J. Koller и K. Brandenburg, "IntMDCT - A link between perceptual and lossless audio coding", Proc. IEEE Int. Conf. on Acoustics, Speech, and Signal Processing, Орландо, штат Флорида, май 2002 г.; и J. Li, "Reversible FFT and MDCT viva matrix lifting", Proc. IEEE Int. Conf. on Acoustics, Speech, and Signal Processing, Монреаль, Канада, май 2004 г.) Однако эти структуры применимы только к модулированному перекрывающемуся преобразованию (MLT), также известному как модифицированное дискретное косинусное преобразование (MDCT), базисные функции которого являются ортогональными и несимметричными (т.е. базисные функции с нелинейной фазой). Эти преобразования не применимы к приложениям сжатия данных, в которых требуются функции линейной фазы (симметричные), таким как цифровое сжатие изображений.

Для сжатия изображений одним из наилучших методов преобразования с точки зрения производительности R-D является перекрывающееся биортогональное преобразование (LBT) (см. S. Malvar, "Biorthogonal and nonuniform lapped transforms for transform coding with reduced blocking and ringing artifacts", IEEE Trans. on Signal Processing, том 46, стр. 1043-1053, апрель 1998 г.) В отличие от MLT базисные функции LBT являются симметричными и неточно ортогональными (в LBT базисные функции анализа являются ортогональными базисным функциям синтеза, отсюда термин "биортогональные"). LBT успешно использовались в приложениях сжатия изображений, но они до сих пор не использовались в сжатии изображений без потерь, поскольку целые обратимые структуры были неизвестны.

Обзор основанного на блочном преобразовании кодирования

Кодирование с преобразованием представляет собой метод сжатия, используемый во многих системах сжатия аудио, изображений и видео. Несжатое цифровое изображение или видео в типовом случае представляется или принимается в виде выборок элементов изображений или цветов в местах на изображении или видеокадре, упорядоченных в двумерной (2D) сетке. Это определяется как представление изображения или видео в пространственной области. Например, типичный формат для изображений состоит из потока 24-битных выборок элементов цветных изображений, упорядоченных в сетке. Каждая выборка является числом, представляющим цветовые компоненты в местоположении пикселя в сетке в цветовом пространстве, таком как RGB или YIQ, помимо прочего. Различные системы изображений и видео могут использовать различные цветовые, пространственные и временные разрешения при дискретизации. Аналогичным образом, цифровое аудио в типовом случае представляется как дискретизированный по времени поток аудиосигналов. Например, типичный формат аудио состоит из потока 16-битных выборок по амплитуде аудиосигнала, взятых с постоянным интервалом времени.

Несжатые цифровые сигналы аудио, изображений и видео могут требовать значительный объем при хранении и передаче. Кодирование с преобразованием уменьшает размер цифрового аудио, изображений и видео посредством преобразования представления сигнала в пространственной области в представление в частотной области (или другой аналогичной области преобразования) и последующего уменьшения разрешения определенных, в общем, в меньшей степени воспринимаемых частотных компонентов представления в области преобразования. Это обычно обуславливает гораздо менее заметное ухудшение цифрового сигнала по сравнению с уменьшением цветового или пространственного разрешения изображений или видео в пространственной области или аудио во временной области.

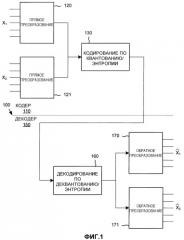
Более конкретно, типичный основанный на блочном преобразовании кодек 100, показанный на фиг.1, делит пиксели несжатого цифрового изображения на двумерные блоки фиксированного размера (), при этом каждый блок, возможно, перекрывается с другими блоками. Линейное преобразование 120-121, которое выполняет анализ пространственных частот, применяется к каждому блоку, что преобразует разнесенные выборки в блоке в набор коэффициентов частот (или преобразования), обычно представляющих интенсивность цифрового сигнала в соответствующих полосах частот по блочному интервалу. Для сжатия коэффициенты преобразования могут быть селективно квантованы 130 (т.е. снижены по разрешению, например, посредством отбрасывания наименее значимых битов значений коэффициентов или иного отображения значений в числовом множестве с более высоким разрешением на меньшее разрешение), а также могут кодироваться 130 посредством энтропийного кодирования или кодирования переменной длины для получения сжатого потока данных. При декодировании коэффициенты преобразования подвергаются обратному преобразованию 170-171, чтобы приблизительно восстановить исходный выбираемый по цвету/пространству сигнал изображения/видео (восстановленные блоки ).

Блочное преобразование 120-121 может быть задано как математическая операция над вектором x размера N. Более часто операцией является линейное умножение, генерирующее выходной сигнал области преобразования , где M - матрица преобразования. Когда входные данные имеют произвольную длину, они сегментируются на N векторов определенной длины и блочное преобразование применяется к каждому сегменту. Для целей сжатия данных выбираются обратимые блочные преобразования. Другими словами, матрица M является обратимой. В случае нескольких измерений (например, для изображения и видео) блочные преобразования обычно реализуются как раздельные операции. Матричное умножение применяется раздельно по каждому измерению данных (т.е. и строк, и столбцов).

Для сжатия коэффициенты преобразования (компоненты вектора y) могут селективно квантоваться (т.е. может уменьшаться их разрешение, например, посредством отбрасывания наименее значимых битов значений коэффициентов или отображения значений в числовом множестве с более высоким разрешением на меньшее разрешение), а также кодироваться с использованием энтропийного кодирования или кодирования переменной длины в сжатый поток данных.

При декодировании в декодере 150 инверсия этих операций (декодированное/энтропийное декодирование 160 и обратное блочное преобразование 170-171) применяется на стороне декодера 150, как показано на фиг.1. При восстановлении данных обратная матрица M ^-1 (обратное преобразование 170-171) применяется в качестве множителя к данным области преобразования. При применении к данным области преобразования обратное преобразование приблизительно восстанавливает исходный цифровой мультимедийный сигнал временной области или пространственной области.

Во многих приложениях кодирования на основе блочного преобразования преобразование предпочтительно обратимое, чтобы поддерживать сжатие как с потерями, так и без потерь в зависимости от коэффициента квантования. При отсутствии квантования (что обычно представляется коэффициентом квантования, равным 1), например, кодек, использующий обратимое преобразование, может точно воспроизводить входные данные при декодировании. Однако требование обратимости в этих приложениях ограничивает выбор преобразований, на основе которых может быть разработан кодек.

Многие системы сжатия изображений и видео, такие как MPEG и Windows Media, помимо прочих, используют преобразования на основе дискретного косинусного преобразования (DCT). DCT, как известно, имеет подходящие свойства энергетического сжатия, что приводит к практически оптимальному сжатию данных. В этих системах сжатия обратное DCT (IDCT) используется в контурах восстановления как в кодере, так и в декодере системы сжатия для восстановления отдельных блоков изображений. DCT описано в публикации N. Ahmed, T. Natarajan, K.R. Rao "Discrete Cosine Transform", IEEE Transactions on Computers, C-23 (январь 1974 г.), на стр. 90-93. Примерная реализация IDCT описана в"IEEE Standard Specification for the Implementations of 8×8 Inverse Discrete Cosine Transform", IEEE Std. 1180-1990, 6 декабря 1990 г.

При сжатии статического изображения (или внутренне закодированного кадра видеопоследовательности) самые распространенные стандарты, такие как MPEG-2, MPEG-4 и Windows Media, разбивают изображение на квадратные мозаики и применяют блочное преобразование к каждому элементу мозаики изображения. Коэффициенты преобразования в данном разделе (общеизвестном как блок) находятся под влиянием только компонентов необработанных данных в блоке. Необратимые операции или операции с потерями на стороне кодера, такие как квантование, служат причиной помех, появляющихся в декодированном изображении. Эти помехи являются независимыми для блоков и генерируют визуально раздражающий эффект, называемый эффектом блокирования. Аналогично для аудиоданных, когда неперекрывающиеся блоки независимо кодируются с преобразованием, ошибки квантования генерируют разрывы в сигнале на границах блоков при восстановлении аудиосигнала в декодере. Для аудио прослушивается эффект периодических щелчков.

Ряд методов используется для противодействия эффекту блокирования. Наиболее популярные среди них - это фильтр деблокирования, который сглаживает границы краев внутренних блоков, и пространственная экстраполяция, которая кодирует различия между необработанными входными данными и прогнозированием от краев соседних блоков. Эти методики имеют свои недостатки. Например, подход с использованием фильтра деблокирования - это "разомкнутый контур", т.е. процесс прямого преобразования не принимает во внимание тот факт, что деблокирование должно выполняться до восстановления на стороне декодера. Кроме того, оба эти метода характеризуются большим объемом вычислений.

Чтобы минимизировать эффект блокирования, могут быть использованы межблочные корреляции. Один способ достижения межблочной корреляции заключается в использовании перекрывающегося преобразования, как описано в публикации H. Malvar, "Signal Processing with Lapped Transforms", Artech House, Норвуд, штат Массачусетс, 1992 г. Перекрывающееся преобразование - это преобразование, входные данные которого распространяется, помимо элементов данных в текущем блоке, на несколько соседних элементов в соседних блоках. Аналогично, на стороне восстановления обратное преобразование влияет на все точки данных в текущем блоке, а также на несколько точек данных в соседних блоках.

В случае двумерных (2D) данных перекрывающееся двумерное преобразование - это функция текущего блока, вместе с выбранными элементами блоков слева, вверху, справа, внизу и, возможно, вверху слева, вверху справа, внизу слева и внизу справа. Количество точек данных в соседних блоках, которые используются для вычисления текущего преобразования, определяется как перекрытие.

Обзор перекрывающегося преобразования пространственной области

Перекрывающееся преобразование может быть реализовано в области преобразования в качестве этапа, который объединяет величины областей преобразования после традиционного блочного преобразования. Кроме того, это может быть реализовано в пространственной области определения посредством стадии предварительной обработки, которая применяется к пикселям в диапазоне перекрытия. Эти две реализации математически связаны и поэтому эквиваленты.

Фиг.2 показывает пример традиционного перекрывающегося преобразования пространственной области. В показанном примере перекрытие составляет два пикселя, и два пикселя, каждый из двух показанных соседних блоков, предварительно обрабатываются на стадии 210 предварительной обработки. Два предварительно обработанных выходных результата отправляются каждому из блоков для кодирования на основе блочного преобразования кодеком 100, как показано на фиг.1. Инверсия стадии предварительной обработки применяется на стадии постобработки 220 после декодирования. При разумном выборе предварительной обработки и блочного преобразования может быть реализован широкий диапазон перекрывающихся преобразований.

Ключевое преимущество реализации в пространственной области перекрывающегося преобразования состоит в том, что используемый основанный на блочном преобразовании кодек может быть модернизирован с помощью стадии предварительной или постобработки для обеспечения преимуществ перекрывающегося преобразования, т.е. уменьшения эффекта блокирования и лучшего сжатия с использованием существующей структуры кодека. Предварительная обработка 210 и постобработка могут быть представлены как матричное умножение, как показано на фиг.3. Традиционно матрицы предварительной и постобработки являются инверсиями друг друга, т.е. перемножение матрицы предварительной обработки (P _f) и инверсной матрицы или матрицы постобработки (P _i) дает единичную матрицу I.

Определения

В общем, длина N преобразования - это число коэффициентов преобразования в конкретном блоке преобразования.

Основа K преобразования - это число точек входных данных, которые оказывают влияние на коэффициенты блока преобразования. Аналогичным образом, это число точек выходных данных, на которые оказывает влияние каждый коэффициент преобразования посредством процесса обратного преобразования.

Для типичных блочных преобразований, таких как дискретное косинусное преобразование (DCT), длина и основа идентичны. Тем не менее, перекрывающиеся преобразования (LT) являются важным классом преобразований, для которых основа K больше, чем длина N. Запись K × N используется для обозначения основы и длины перекрывающегося преобразования. (Преобразования, для которых K < N, являются обширными и поэтому не используются в сжатии данных).

В качестве примера 300 LT 310 6×4, показанное на фиг.3, является преобразованием с шестью входами и четырьмя выходами. Поскольку преобразование является обратимым, два входа совместно используются соседними блоками преобразования. Обратное перекрывающееся преобразование (ILT) 320 генерирует шесть выходных результатов из своих четырех входов. Выходные точки данных рядом с границей блоков (в данном случае одна точка в каждом конце блока) восстанавливаются посредством суммирования соответствующих откликов от двух соседних блоков обратного преобразования.

Ограничения на перекрывающиеся преобразования, используемые в системах сжатия

В математическом смысле перекрывающиеся преобразования - это обратимые структуры, если рассматривать входные и выходные сигналы, а также результаты промежуточных вычислений как реальные числа. Если бы могла быть достигнута бесконечная точность, то входные данные можно было бы полностью восстановить из своих коэффициентов перекрывающегося преобразования. Однако бесконечная точность невозможна на практике; для сжатия данных без потерь требование состоит в том, чтобы спроектировать преобразование, которое осуществляет операции над целыми числами или с заданной точностью, тем не менее, полностью восстанавливает данные, дающие целочисленное представление коэффициентов преобразования. Это более строгое условие, чем математическая обратимость, и такое преобразование определяется в данном документе как преобразование "без потерь". Более того, требуется, чтобы преобразование без потерь было также эффективным и для сжатия данных (как без потерь, так и с потерями). Эта эффективность может быть измерена посредством энтропии преобразованных данных; чем ниже эта энтропия, тем больше преобразованные данные могут быть сжаты посредством стандартных методов энтропийного кодирования, таких как основанное на контексте арифметическое кодирование или адаптивное кодирование по длинам серий.

Сущность изобретения

В данном документе описаны различные реализации эффективного перекрывающегося преобразования, которое обратимо в целочисленной арифметике и может быть использовано в качестве основы системы эффективного сжатия/восстановления данных без потерь.

Может быть показано, что наиболее эффективные структуры преобразования без потерь (т.е. структуры с минимальной энтропией преобразованных данных) требуют, чтобы матрица преобразования была единичной детерминантной (т.е. детерминант матрицы преобразования равен ±1). В последующем описании предполагается, что преобразование может быть представлено как матричное умножение, хотя очевидно, что может быть незначительные нелинейные явления, такие как округление данных. Таким образом, при ссылке на детерминант аспекты усечения и округления не рассматриваются.

Эффективное перекрывающееся преобразование реализуется с помощью предварительных и постфильтров, которые определяются в данном документе как "операторы перекрытия". Эта реализация обратимая, хотя очень эффективная по R-D. Среди других приложений эти новые операторы перекрытия позволяют реализовать обратимые LBT, которые могут быть использованы для сжатия изображений без потерь. Предварительные и постфильтры используют обратимые операции. Дополнительно описанные операторы перекрытия включают в себя упрощения для обеспечения вычислительной эффективности.

Одна реализация операции предварительной и пост-фильтрации использует оператор одномерного обратимого перекрытия, который структурирован из единичных детерминантных матриц компонентов. Более конкретно, оператор обратимого перекрытия реализован как последовательность плоских поворотных преобразований и единичных детерминантных плоских масштабных преобразований. Плоские масштабные преобразования могут быть реализованы с помощью этапов планарных сдвигов или поднятий. Дополнительно плоские повороты и плоские сдвиги имеют реализацию в качестве обратимых операций без потерь, предоставляя в качестве результата оператор обратимого перекрытия.

Типичным применением является одномерное перекрывающееся преобразование 8×4, реализованное с использованием вычислительно эффективных аппроксимаций операторов обратимого перекрытия.

Для двумерного перекрывающегося преобразования эта одномерная реализация оператора перекрытия может быть применена отдельно к горизонтальным строкам блока цифровых мультимедийных данных, после чего применяется одномерный оператор к вертикальным столбцам данных. Этот подход имеет несколько недостатков, наиболее серьезными из которых являются:

1) трудность или практически невозможность получения нормализованного предварительного/постфильтра для эффективного сжатия данных,

2) высокая степень сложности, если такое приближение может быть достигнуто, и

3) неточность вследствие нескольких этапов фильтрация/поднятие при реализации этого приближения.

Альтернативная реализация двумерного перекрывающегося преобразования, описанная в данном документе, достигает более высокую вычислительную эффективность, чем подход раздельного горизонтального и вертикального применения оператора одномерного перекрытия. Эта альтернативная реализация разделяет оператор одномерного перекрытия на две стадии и перемежает стадии горизонтального и вертикального применения оператора перекрытия. В рамках каждой стадии операция нормализованного масштабирования, реализованная на этапах поднятия, может быть применена к более ограниченным подмножества блоков данных (например, подмножествам 2×2 или сигнальным парам блока данных 4×4), имея ввиду компенсацию "перекрестных членов" в двумерной структуре с перемежением. Это приводит к эффективному масштабно-инвариантному двумерному предварительному/постфильтру.

Двумерный предварительный/постфильтр может быть объединен с обратимым преобразованием, например эффективным масштабно-инвариантным обратимым двумерным преобразованием, описанным в патентной заявке США 11/015707 на имя Srinivasan, озаглавленной "Reversible Transform For Lossy And Lossless 2-D Data Compression", от 17 декабря 2004 года. Объединенный предварительный/пост-фильтр и преобразование формируют перекрывающееся преобразование, которое может быть использовано для точного и эффективного в вычислительном отношении сжатия изображений и видео, как с потерями, так и без потерь.

Дополнительные признаки и преимущества поясняются в последующем подробном описании вариантов осуществления со ссылками на прилагаемые чертежи.

Краткое описание чертежей

Фиг.1 - блок-схема традиционного основанного на блочном преобразовании кодека согласно предшествующему уровню техники.

Фиг.2 - блок-схема перекрывающегося преобразования пространственной области, реализованного в качестве операций предварительной и постфильтрации в сочетании с основанным на блочном преобразовании кодеком фиг.1, также согласно предшествующему уровню техники.

Фиг.3 - блок-схема, иллюстрирующая пару перекрывающегося преобразования и обратимого перекрывающегося преобразования на одномерных данных.

Фиг.4 - блок-схема алгоритма кодера, основанного на перекрывающемся преобразовании, использующем оператор обратимого перекрытия.

Фиг.5 - блок-схема декодера, основанного на перекрывающемся преобразовании.

Фиг.6 - блок-схема, иллюстрирующая пару перекрывающегося преобразования и обратного перекрывающегося преобразования на одномерных данных с использованием операций предварительной и постфильтрации (или оператор обратимого перекрытия) совместно с блочным преобразованием.

Фиг.7 - сигнальный ориентированный граф, иллюстрирующий структуру предварительного или постфильтра линейной фазы для использования в качестве оператора обратимого перекрытия в перекрывающемся преобразовании по фиг.6.

Фиг.8 - сигнальный ориентированный граф масштабирования без потерь в виде четырех этапов поднятия для использования в операторе обратимого перекрытия.

Фиг.9 - сигнальный ориентированный граф масштабирования без потерь в виде пяти этапов поднятия для использования в операторе обратимого перекрытия.

Фиг.10 - сигнальный ориентированный граф каскадного 2-точечного масштабирования, применяемого к матрице большей размерности для реализации единичного детерминантного масштабирования без потерь.

Фиг.11 - сигнальный ориентированный граф оператора обратимого перекрытия (или предварительного/постфильтра), имеющего структуру, показанную на фиг.7, и использующего единичное детерминантное масштабирование без потерь по фиг.10.

Фиг.12 - блок-схема алгоритма работы оператора обратимого перекрытия по фиг.11.

Фиг.13 - сигнальный ориентированный граф, иллюстрирующий пример реализации обратимого перекрывающегося преобразования, использующего оператор обратимого перекрытия по фиг.11.

Фиг.14 - граф импульсной характеристики коэффициента постоянной составляющей примерного перекрывающегося преобразования по фиг.13.

Фиг.15 - схема, иллюстрирующая пиксели, используемые в качестве основы оператора двумерного перекрытия для блоков размером 4×4.

Фиг.16 - схема, иллюстрирующая пиксели, используемые в качестве основы оператора двумерного перекрытия для блоков размером 2×2.

Фиг.17 - блок-схема последовательности операции способа преобразования, применяемого на стороне кодера по фиг.4.

Фиг.18 - блок-схема последовательности операции способа преобразования, применяемого на стороне декодера по фиг.5.

Фиг.19 - сигнальный ориентированный граф, предоставляющий каноническое представление оператора одномерного обратимого преобразования, показанного на фиг.11.

Фиг.20 - сигнальный ориентированный граф, иллюстрирующий двумерный предварительный/постфильтр, реализованный посредством раздельного применения оператора одномерного обратимого преобразования по фиг.19 по горизонтали и по вертикали.

Фиг.21 - сигнальный ориентированный граф, иллюстрирующий двумерный предварительный/постфильтр для обратимого преобразования, реализованного посредством чередования горизонтальных и вертикальных операций двумерного фильтра в стадиях.

Фиг.22 - листинг программы на языке программирования C для реализации нормализованного оператора Адамара 2×2, который формирует часть двумерного предварительного/постфильтра по фиг.21.

Фиг.23 - схема, показывающая соответствие между точками данных, обрабатываемыми с помощью предварительного/постфильтра 2×2.

Фиг.24 - схема, иллюстрирующая точки данных блока данных 4×4, к которому применяется оператор Адамара 2×2 на первой стадии реализации двумерного предварительного/постфильтра 4×4 фиг.21.

Фиг.25 - листинг программы на языке программирования C для реализации прямого поворота, которое формирует часть двумерного предварительного фильтра фиг.21.

Фиг.26 - листинг программы на языке программирования C для реализации обратного поворота, которое формирует часть двумерного постфильтра фиг.21.

Фиг.27 - листинг программы на языке программирования C для реализации прямого 2-точечного поворота, которое формирует часть двумерного предварительного фильтра фиг.21.

Фиг.28 - листинг программы на языке программирования C для реализации обратного 2-точечного поворота, которое формирует часть двумерного постфильтра по фиг.21.

Фиг.29 - схема, иллюстрирующая точки данных блока данных 4×4, к которому применяются повороты по фиг.25-28 на другой стадии реализации двумерного предварительного/постфильтра 4×4 по фиг.21.

Фиг.30 - схема, иллюстрирующая точки данных блока данных 4×4, к которому применяются 2-точечные операции масштабирования на дополнительной стадии реализации двумерного предварительного/постфильтра 4×4 по фиг.21.

Фиг.31 - листинг программы на языке программирования C для реализации прямого масштабирования, которое формирует часть двумерного предварительного фильтра по фиг.21.

Фиг.32 - листинг программы на языке программирования C для реализации обратного масштабирования, которое формирует часть двумерного постфильтра по фиг.21.

Фиг.33 - листинг программы на языке программирования C для реализации двумерного предварительного фильтра 4×4 по фиг.21.

Фиг.34 - листинг программы на языке программирования C для реализации двумерного постфильтра 4×4 по фиг.21.

Фиг.35 - листинг программы на языке программирования C для реализации двумерного предварительного фильтра 2×2.

Фиг.36 - листинг программы на языке программирования C для реализации двумерного постфильтра 2×2.

Фиг.37 - листинг программы на языке программирования C для реализации одномерного 2-точечного предварительного фильтра для применения на краях изображений, имеющих недостаточное число точек данных для двумерного предварительного фильтра по фиг.35.

Фиг.38 - листинг программы на языке программирования C для реализации одномерного 2-точечного постфильтра для применения на краях изображений, имеющих недостаточное число точек данных для двумерного предварительного фильтра по фиг.36.

Фиг.39 - листинг программы на языке программирования C для реализации одномерного 4-точечного предварительного фильтра для применения на краях изображений, имеющих недостаточное число точек данных для двумерного предварительного фильтра по фиг.33.

Фиг.40 - листинг программы на языке программирования C для реализации одномерного 4-точечного постфильтра для применения на краях изображений, имеющих недостаточное число точек данных для двумерного предварительного фильтра по фиг.34.

Фиг.41 - листинг программы на языке программирования C для реализации прямого преобразования, используемого в сочетании с предварительным фильтром по фиг.21 для осуществления перекрывающегося преобразования в кодере по фиг.4.

Фиг.42 - листинг программы на языке программирования C для реализации преобразования, которое формирует часть прямого преобразования по фиг.41.

Фиг.43 - листинг программы на языке программирования C для реализации еще одного преобразования, которое формирует часть прямого преобразования по фиг.41.

Фиг.44 - листинг программы на языке программирования C для реализации прямого преобразования, используемого в сочетании с предварительным фильтром по фиг.21 для осуществления перекрывающегося преобразования в кодере по фиг.5.

Фиг.45 - листинг программы на языке программирования C для реализации преобразования, которое формирует часть обратного преобразования по фиг.44.

Фиг.46 - листинг программы на языке программирования C для реализации другого преобразования, которое формирует часть обратного преобразования по фиг.44.

Фиг.47 - блок-схема подходящей вычислительной среды для реализации основанного на блочном преобразовании кодека с помощью усовершенствованного перекрывающегося преобразования пространственной области по фиг.4 и 5.

Подробное описание изобретения

Последующее описание относится к системе сжатия или кодеку цифрового мультимедийного сигнала, который использует обратимую двумерную предварительную/постфильтрацию для перекрывающегося преобразования. В целях иллюстрации вариантом осуществления системы сжатия, содержащей в себе такую двумерную предварительную/постфильтрацию, является система сжатия изображений или видео. Альтернативно, оператор обратимого перекрытия также может быть включен в системы сжатия или кодеки для других двумерных данных. Оператор обратимого перекрытия не требует, чтобы система сжатия цифрового мультимедийного сигнала кодировала сжатые цифровые мультимедийные данные в конкретном формате кодирования.

1. Кодер/декодер

На фиг.4 и 5 показана обобщенная диаграмма процессов, используемых в репрезентативном двумерном (2D) кодере 400 и декодере 500 данных, основанном на перекрывающемся преобразовании, использующем оператор обратимого перекрытия. Схемы представляют обобщенную или упрощенную иллюстрацию использования и применения данного оператора обратимого перекрытия в системе сжатия, содержащей кодер и декодер двумерных данных. В альтернативных кодерах, основанных на этом операторе обратимого перекрытия, для сжатия двумерных данных может быть использовано дополнительное или меньшее число процессов, чем проиллюстрировано в репрезентативном кодере и декодере. Например, некоторые кодеры/декодеры могут также включать в себя цветовое преобразование, форматы цветов, масштабируемое кодирование, кодирование без потерь, режимы макроблоков и т.д. Система сжатия (кодер и декодер) может предоставлять кодирование двумерных данных без потерь и/или с потерями, в зависимости от квантования, которое может быть основано на параметре квантования, варьирующемся от варианта без потерь до варианта с потерями.

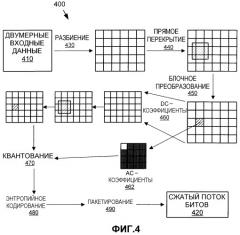
Кодер 400 двумерных данных генерирует сжатый поток 420 битов, который является более компактным представлением (для типичного ввода) двумерных данных 410, представляемых в качестве входного сигнала кодеру. Например, входными двумерными данными могут являться изображение, кадр видеопоследовательности или другие данные, имеющие два измерения. Кодер двумерных данных разбивает (430) входные данные на макроблоки, которые имеют размер 16×16 пикселей в данном репрезентативном кодере. Кодер двумерных данных дополнительно разбивает каждый макроблок на блоки 432 размером 4×4. Оператор 440 "прямого перекрытия" применяется к каждому краю между блоками, после чего каждый блок 4×4 преобразуется с помощью блочного преобразования 550. Этим блочным преобразованием 450 может быть обратимое масштабно-инвариантное двумерное преобразование, описанное в патентной заявке США 11/015707, озаглавленной "Reversible Transform For Lossy And Lossless 2-D Data Compression", на имя Srinivasan, от 17 декабря 2004 г. Альтернативно, дискретное косинусное преобразование или другие блочные преобразования могут быть использованы с оператором обратимого перекрытия, описанным в данном документе. В результате преобразования коэффициент 460 постоянной составляющей каждого блока преобразования размером 4×4 проходит аналогичную цепочку обработки (разбиение, прямое перекрытие, за которым следует блочное преобразование 4×4). Результирующие коэффициенты преобразования постоянной составляющей и коэффициенты преобразования переменной составляющей квантуются (470), подвергаются энтропийному кодированию (480) и пакетируются (490).

Декодер выполняет обратный процесс. На стороне декодера биты коэффициентов преобразования извлекаются (510) из соответствующих пакетов, из которых сами коэффициенты декодируются (520) и деквантуются (530). Коэффициенты 540 постоянной составляющей регенерируются посредством применения обратного преобразования, и плоскость коэффициентов постоянной составляющей "перекрывается в обратном порядке" с использованием подходящего сглаживающего оператора, применяемого по краям блока постоянной составляющей. В дальнейшем все данные регенерируются посредством применения обратного преобразования 550 размером 4×4 к коэффициентам постоянной составляющей, и коэффициенты 542 переменной составляющей декодируются из потока битов. Наконец, края блока в плоскостях результирующих изображений фильтруются (560) с обратным перекрытием. В результате генерируются восстановленные выходные двумерные данные.

В примерной реализации кодер 400 (фиг.4) сжимает входное изображение для получения сжатого потока 420 битов (например, файла), а декодер 500 (фиг.5) восстанавливает исходные входные данные или их приближение на основе того, какое кодирование (с потерями или без потерь) используется. Процесс кодирования влечет за собой применение прямого перекрывающегося преобразования (LT), описанного ниже, которое реализовано с помощью обратимой двумерной предварительной/постфильтрации, также более подробно описанной ниже. Процесс декодирования осуществляется посредством обратного перекрывающегося преобразования (ILT) с использованием обратимой двумерной предварительной/постфильтрации.

Проиллюстрированные преобразования LT и ILT являются инверсиями друг друга, в точном смысле, и поэтому вместе могут определяться как обратимое перекрывающееся преобразование. В качестве обратимого преобразования пара LT/ILT может быть использована для сжатия изображений без потерь.

Входными данными 410, сжатыми кодером 400/декодером 500, могут быть изображения различных форматов цветов (например, форматы цветных изображений RGB/YUV4:4:4 или YUV4:2:0). В типовом случае входное изображение всегда имеет компонент яркости (Y). Если оно является изображением RGB/YUV4:4:4 или YUV4:2:0, то изображение также имеет компоненты цветности, такие как компонент U и компонент V. Отдельные цветовые плоскости или компоненты изображения могут иметь различные пространственные разрешения. В случае входного изображения, напр